Значение формулы. Что такое формула в математике.

Мы создали сложные механические модели, чтобы доказать математику «точно», но в процессе потеряли интуитивное понимание предмета.

Математика в формулах и таблицах Справочное пособие

Учебник содержит формулы, таблицы и диаграммы по математике, охватывающие важнейшие разделы элементарной математики — алгебру и геометрию. Он предназначен для абитуриентов, готовящихся к вступительным экзаменам в университет, студентов дневного и заочного отделений, изучающих высшую математику и другие дисциплины.

Факультет высшей математики

Одобрено в качестве учебника редакционно-издательским комитетом СибГУТИ.

Сибирский государственный университет телекоммуникаций и информатики, 2000.

В.И.Агульник, Б.П.Зеленцов, 2000.

Оглавление

1. ЧИСЛА, ДРОБИ, МОДУЛИ…………………………………
2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ …………
3. СТЕПЕНИ И КОРНИ ……………………………………….
4. КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА ………
5. ПРОГРЕССИИ ………………………………………………
6. ЛОГАРИФМЫ ………………………………………………
7. ТРИГОНОМЕТРИЯ ………………………………………
8. ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ……………
9. ПЛАНИМЕТРИЯ …………………………………………
10. СТЕРЕОМЕТРИЯ …………………………………………

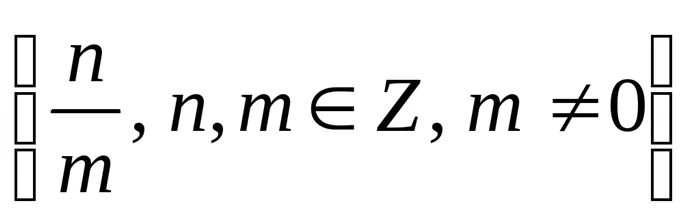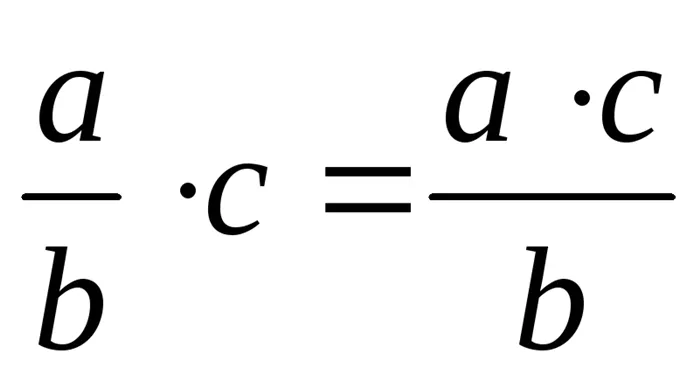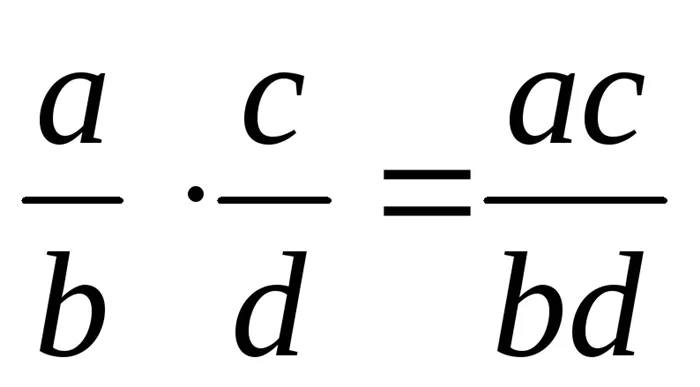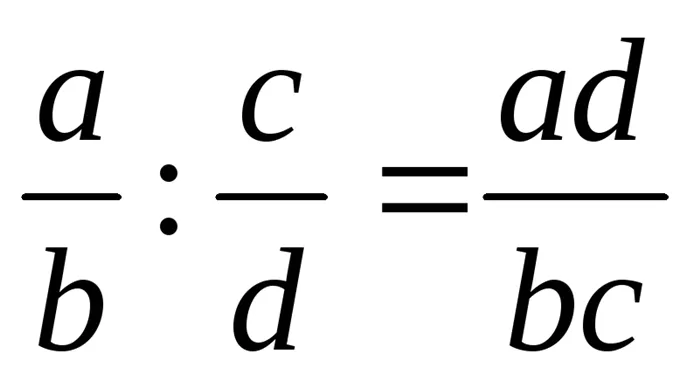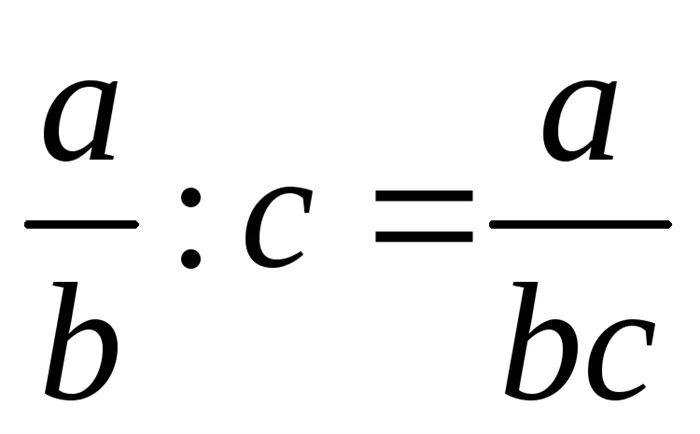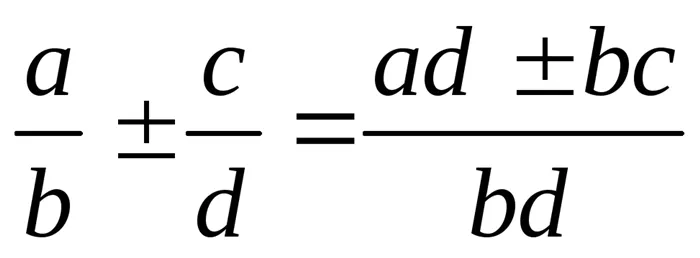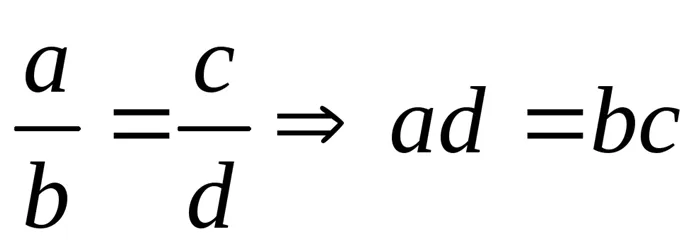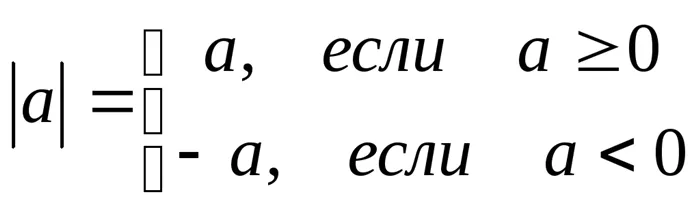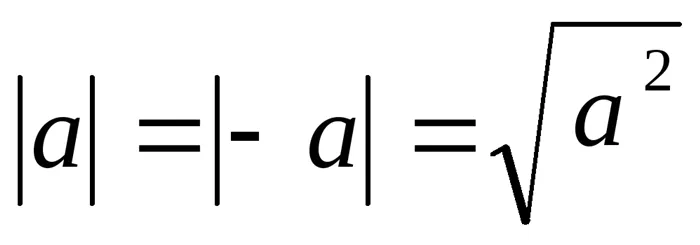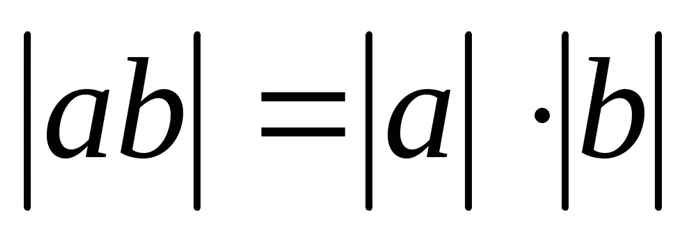
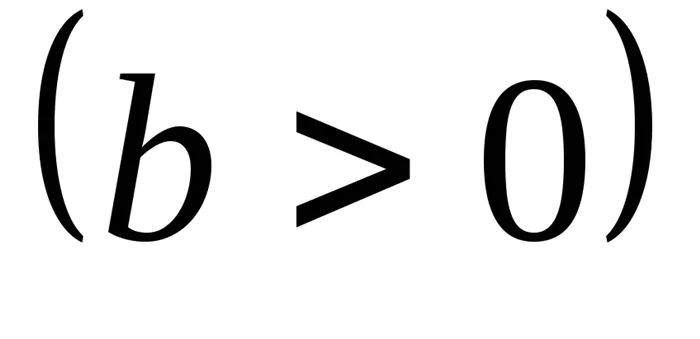n  N — множество натуральных чисел d = НОД ( n, m ) — наибольший общий делитель n и mk = НОК ( n, m ) — наименьшее общее кратное n и mZ =множество целых чисел Q =— множество рациональных чисел (дробей) R – множество действительных чисел Арифметические операции с дробями:;;;;;; Пропорция; Модуль числа. Определение:; Свойства модуля:;;; a a+b a-b; x; a a+b a-b x 2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ;;;;;;; 3. СТЕПЕНИ И КОРНИ;;;;;;;;;;;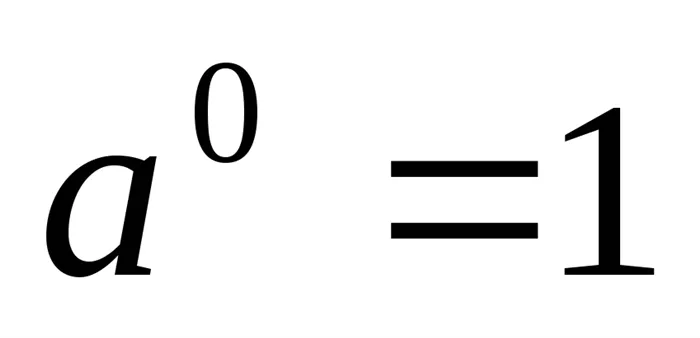

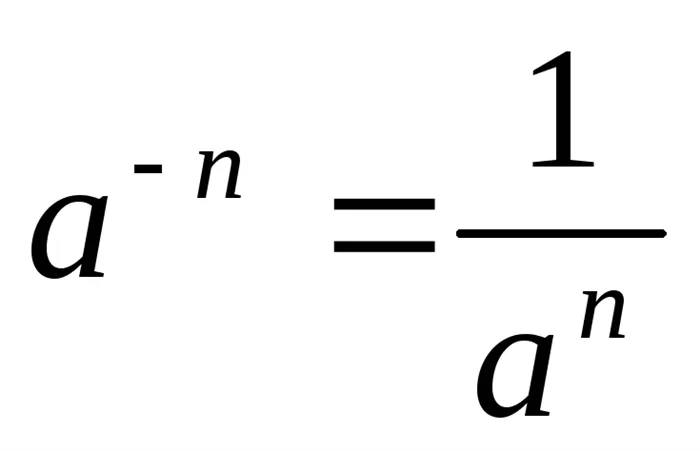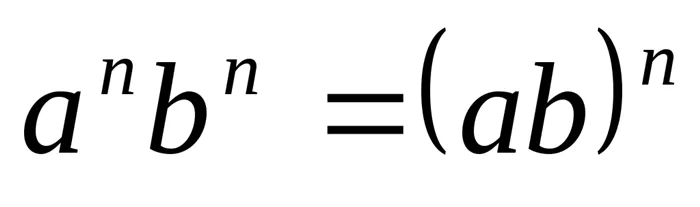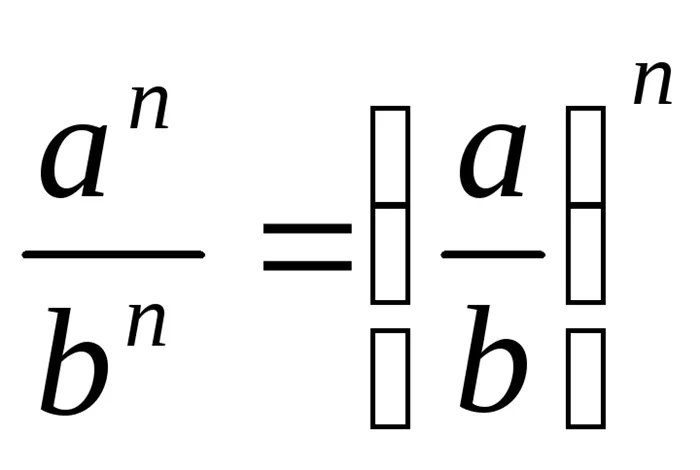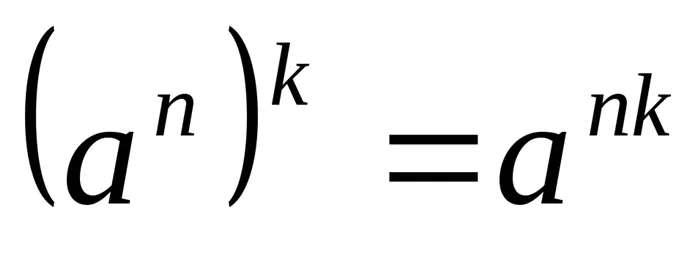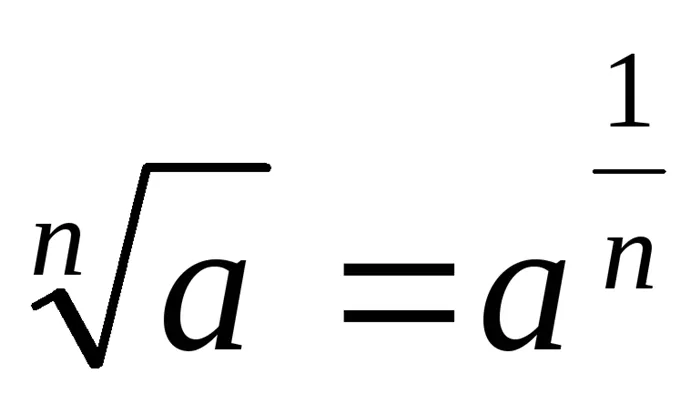Квадратные уравнения

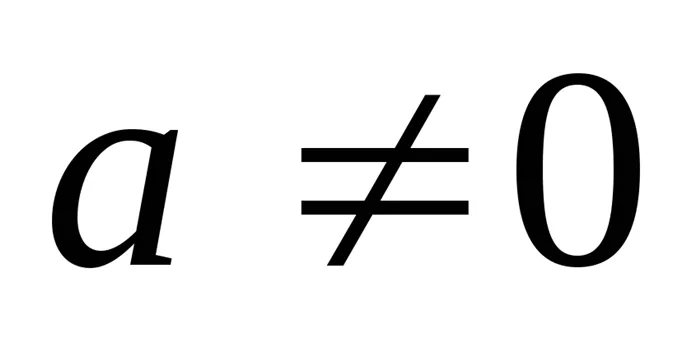;Корни уравнения: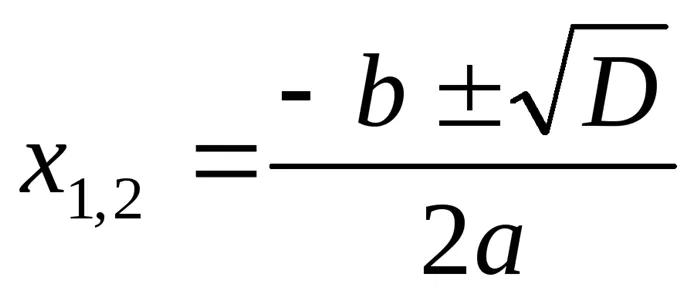, где — дискриминант. Формулы Виета: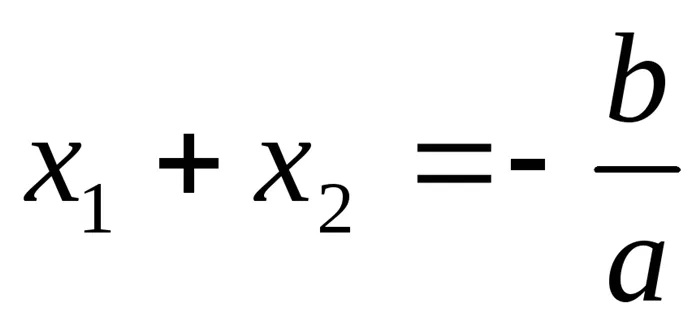;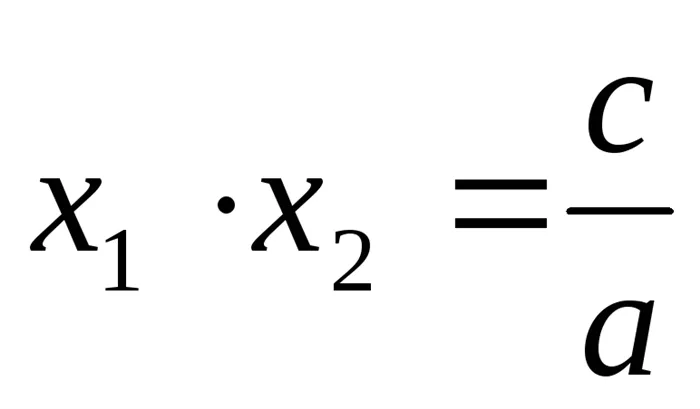. Разложение квадратного трехчлена на множители:. Приведенное уравнение:;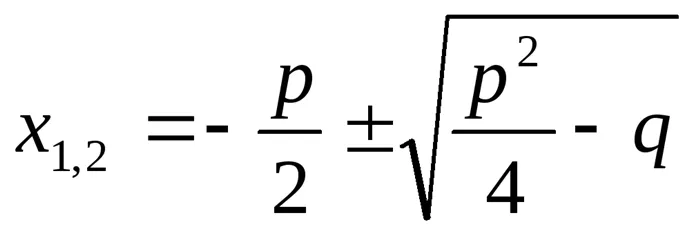. Квадратное неравенство: Если D>0, a>0,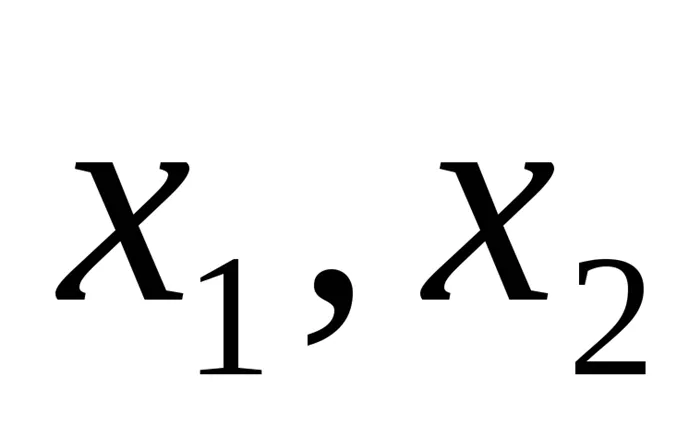— корни квадратного трехчлена,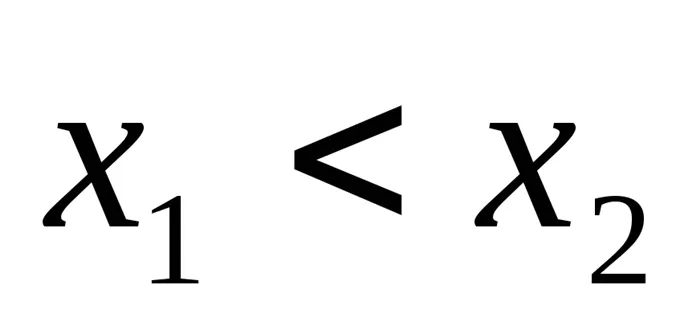, то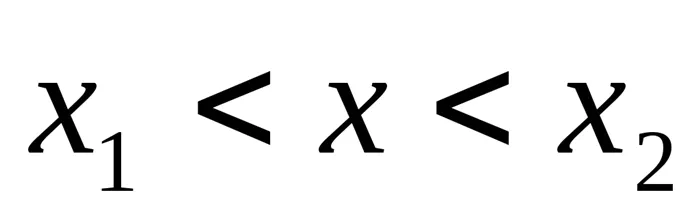;. 5. ПРОГРЕССИИ Арифметическая прогрессия:Общий член:,, где— разность прогрессии;Сумма членов. Геометрическая прогрессияОбщий член:, где— знаменатель прогрессии;Сумма членов. Сумма геометрической прогрессии (при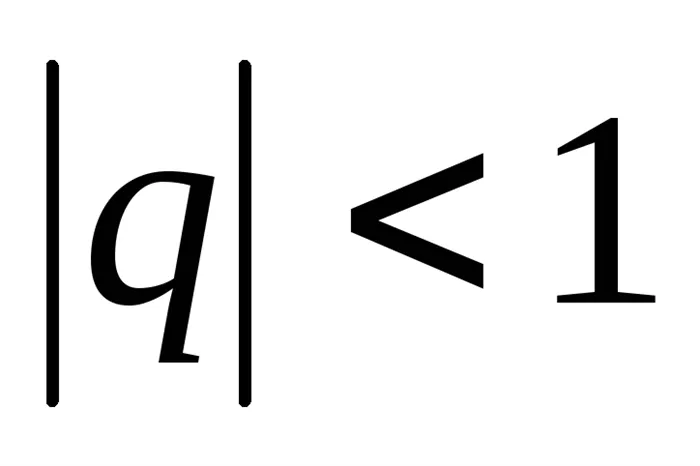):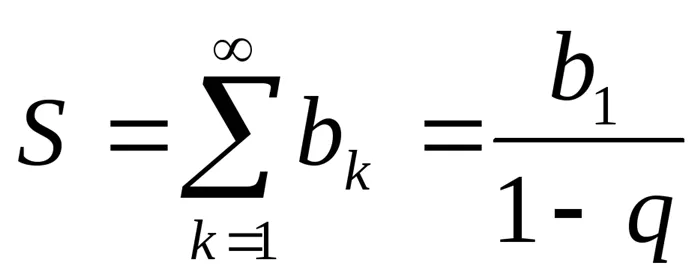. Некоторые суммы:;;;;; 6. ЛОГАРИФМЫ Логарифм числа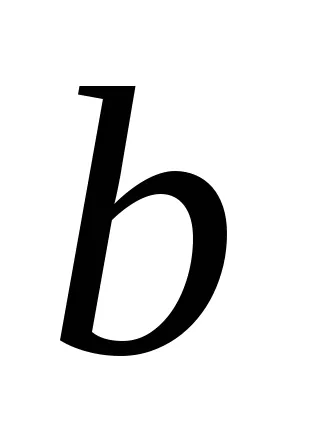по основанию:. Основное логарифмическое тождество: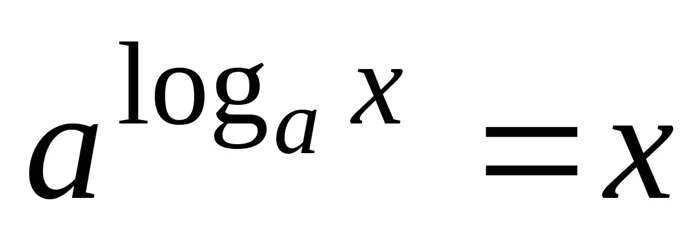. Свойства логарифмов:;;;;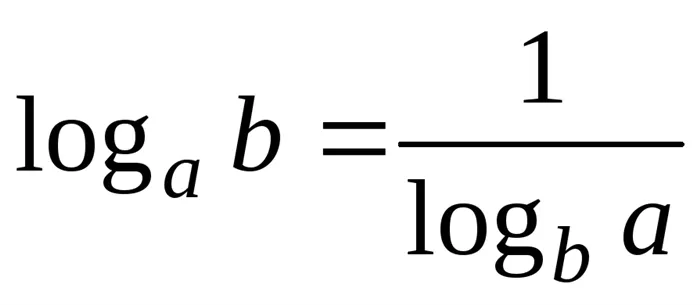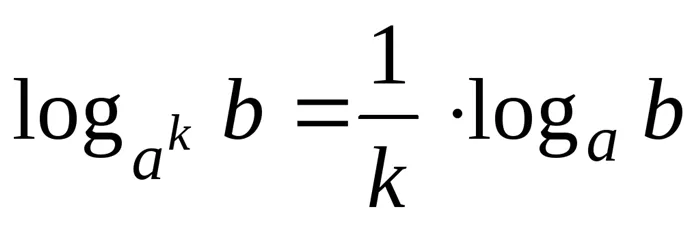. Десятичные лога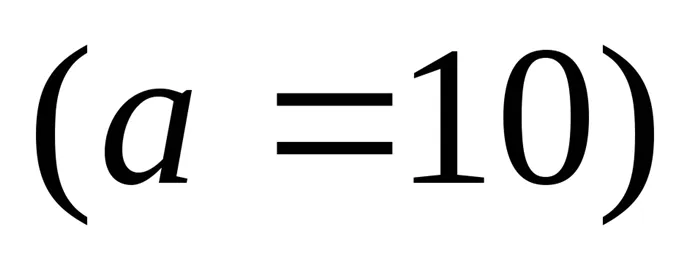рифмы:. Натуральные логарифмы: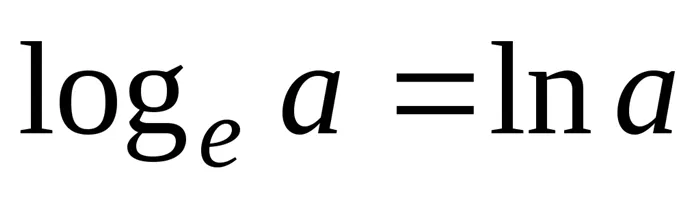. Логарифмические неравенства:. Показательные неравенства:. 7. ТРИГОНОМЕТРИЯ

Формула в математике

В науке формулами называют набор основных операций, которые с помощью символов и числовых значений позволяют решать арифметические операции и выводить определенные результаты.

Формулы в науке могут быть математическими формулами, геометрическими формулами, физическими формулами, химическими формулами, статистическими формулами и другими. Этот тип формулы обычно представлен уравнением.

В математике формулы или уравнения часто используются для вычисления дробей, степеней, метрической системы, производных, интегралов и т.д. Д.

Формула для вычисления дробей

В геометрии формулы используются для вычисления углов, векторов, площадей и т.д. Пример:

Пифагорейская теорема

В физике формулы можно использовать для экстраполяции таких данных, как вес, движение, скорость, масса, объем, сила и ускорение тел. Пример:

Формула для расчета скорости, расстояния и времени движения тела.

В химии формулы представляют элементы, входящие в состав соединения, и количество содержащихся в нем атомов. Например, формула воды: CHAS₂или GER, что означает «две молекулы водорода к одной молекуле кислорода».

Статистика и социальные науки используют формулы для определения потребностей общества. Они позволяют рассчитать плотность населения, смертность или рождаемость, ВВП, ВВП на душу населения и т.д. Д.

См. также статистику.

Фармакологическая формула

В фармакологических формулах они означают ингредиенты и их количество, которые должно содержать данное вещество, чтобы оказать определенное действие.

В дополнение к общим фармакологическим формулам, существуют также магистральные формулы. Стандартные формулы относятся к лекарствам или химическим препаратам, таким как кремы, мази или капли, которые были разработаны для рецептурных потребностей конкретного пациента.

Бесплатная формула

Формулы вежливости означают набор символов и особую заботу при взаимодействии с третьими лицами, чтобы они чувствовали себя комфортно, их уважали и ценили.

Формула-1 — самый известный чемпионат по автоспорту в мире. Он был основан в 1950 году. В чемпионате участвуют такие команды, как Ferrari, Mercedes, Toro Rosso, Renault, Haas, Force India, Sauber, Red Bull, McLaren и Williams.

Формулы. — онлайн урок

Тема: 7 класс типы. Какие существуют типы? Как их использовать, где используются формулы в математике, формулы в физике. Урок отвечает на следующие вопросы: является ли формула математическим законом? Как написать формулу?

Формулы.

Давайте еще раз пройдемся по определениям, которые вы уже знаете и которые мы будем использовать в нашем уроке.

Математическая модель — это способ описания реальной ситуации или проблемы с помощью математического языка.

Математическое выражение — это одно или несколько чисел, связанных с математическими операциями.

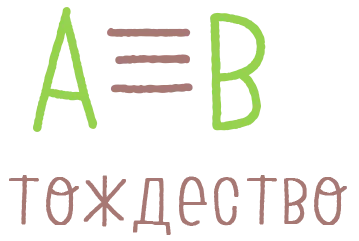
Равенство двух выражений A = B называется тождеством, если оно преобразуется в действительное числовое равенство для каждого значения переменных, для которых определены A и B, т.е. если оно имеет смысл.

Теперь установите соответствие между картинками и определениями, которые мы только что повторили.

Прежде чем мы приступим к основной части урока, я хотел бы перечислить, что мы будем изучать сегодня:

Для продолжения урока кликните на кнопку ниже:

Мне очень нравятся отношения и понимание, которые складываются между учителем и учеником. Это важный момент. Материал представлен в простой и понятной форме. Спасибо!

Отличный учитель! Она все очень понятно объясняет детям, математика стала любимым предметом. Спасибо.

Если бы я мог поставить ему 10 баллов, я бы поставил. Для меня мерилом успеха учителя является мнение моей дочери. Она заинтересована и все понимает. Учитель очень спокойно и уравновешенно объясняет материал. Ему действительно удается рассматривать все в контексте. Екатерина спасла нам жизнь, потому что в школе нет учителя математики, учебная программа отдана на милость родителей. Спасибо, и я преклоняюсь перед ней за то, что моей дочери нравится дистанционное обучение и она осваивает программу средней школы.

Действия с составными существительными. Новые единицы площади (n)

Задача 24 (C4): Задача геометрического расчета. Четырехугольники

Запишитесь на пробный урок

Ежедневно с 10.00 до 22.00 по московскому времени.

Copyright © 2011 — 2022 MyAlfaSchool.com. Все права защищены

• Как с нами связаться
• Уроки по математике
• Статьи
• Правила школы
• Лицензия

• Начать преподавать
• Политика конфиденциальности
• Пользовательское соглашение
• Технические требования
• Оферта для преподавателей

Нажимая кнопку «Бесплатное обучение», вы даете согласие на обработку персональных данных в соответствии с Политикой конфиденциальности.

Значение слова «формула» в словарях русского языка

Формула это:

Формула (от — форма, правило, рецепт):

Формула

1. набор математических величин, выраженных условными символами в их функциональных отношениях (в математике).

2. общее выражение для обозначения состава сложных веществ и химических процессов (в химии).

3. точное и краткое словесное определение чего-либо.

Большой современный словарь русского языка.

Формула

(Лат. formula, form, rule) 1. Точное общее определение какого-либо правила, поведения, закона и т.д., применимый при определенных условиях ко всем особым случаям; вообще, любое определение, выраженное в сокращенной форме; 2) математический набор величин, выраженных цифрами и буквами и связанных с математическими знаками; 3) хим. сокращенное обозначение состава любого соединения с помощью букв латинского алфавита, заменяющих названия элементов, и цифр, указывающих на количество этих элементов в данном соединении (например, nacl, H 2 O).

Формула

ж. 1) Ряд математических величин в их функциональных отношениях, выраженных в условных символах (в математике). 2) Условное выражение для обозначения синтеза сложных веществ и химических процессов (в химии). 3) Rev. Точное и краткое словесное определение того, что есть.

Новый словарь Ефремовой для русского языка.

Формула

1. точное общее определение правила, отношения, закона и т.д., применимое при определенных условиях ко всем конкретным случаям; в целом, любое определение, выраженное в краткой форме,

2. ряд величин, выраженных цифрами и буквами и связанных с математическими символами,

3. химическая аббревиатура для обозначения состава соединения, где буквы латинского алфавита заменяют названия элементов, а цифры указывают на количественное соотношение элементов в соединении (например, nacl, h2o).

Формула

Формула — это комбинация математических символов, которая выражает утверждение. Алгебраическая формула — это краткое и точное словесное выражение, определение высказывания в кратких формулах.

Формула

(лат. formula — картина, вид), комбинация математических символов, выражающая определенное утверждение; например, формула a2 + b2 = c2 выражает связь между длиной c гипотенузы прямоугольного треугольника и длинами a и b его перпендикуляров.

Формула

Формула ж. 1) Набор математических величин, выраженных в условных символах в их функциональных отношениях (в математике). 2) Условное буквенное выражение для обозначения состава сложных веществ и химических процессов (в химии). 3) Rev. Точное и краткое словесное определение чего-либо.

Формула

Формула, ж. (от лат. formula, буквально уменьшенное от forma).

(1) Общее краткое и точное выражение (мысли, закона); определение (библиографическое). -…Первую фазу коммунизма, социализм, мы, по существу, уже осуществили. Основным принципом этой фазы коммунизма, как вы знаете, является формула: «От каждого по способностям, каждому по труду». Сталин. Формула закона всемирного тяготения.

2. выражается в условных символах как ряд математических величин в их функциональных отношениях (мат.).

3. условное буквенное выражение состава сложных веществ и химических процессов (хим.). Химическая формула. Формула серной кислоты. Формула сгорания.

Где и как употребляется слово «формула»?

Помимо значения слова «формула» в словарях, мы также рекомендуем вам изучить примеры предложений и отрывков из классической литературы, в которых употребляется слово «формула».

Таким образом, вам будет гораздо легче понять и запомнить правильное употребление слова «тип» в тексте и языке.

Примеры употребления слова «формула»

— Вы ожидаете, что я дам вам математическую формулу для идеальной победы», — предположил он.

Поэтому здесь вы не найдете магических формул, способных нанести вред — мощных амулетов, костюмов, методов уничтожения.

Группа писателей, 3333 психические припадки. Секретный метод мощного вызывания денег, здоровья, любви и защиты.

Во-первых, он, вероятно, проводит все свои отпуска где-нибудь в горах на свежем воздухе и никогда не будет сидеть в доме, создавая новые химические типы.

Как понимать математические формулы – Как читать математику / Habr

Первоначально формулы были придуманы математиками для описания простых физических явлений. Например, формула для скорости: скорость = расстояние/время. В нем говорится, что если мы движемся с одинаковой скоростью, то за определенное время мы проходим определенное расстояние. Таким образом, он показывает взаимосвязь между двумя переменными: Расстояние и время. Если два человека преодолевают одно и то же расстояние с разной скоростью, они затратят разное количество времени, и первым финиширует тот, кто бежал быстрее всех.

Поэтому необходимы формулы, чтобы более точно (с помощью математических символов или букв) передать взаимосвязь между определенными величинами (см. пример в статье).

Решение задач с формулами обычно сводится к нахождению величины по знанию других величин в формуле.

Закон Ома выражается формулой U = I-R, где U — напряжение в вольтах, I — сила тока в амперах, а R — сопротивление в омах. Если ток равен 2 амперам, а сопротивление 10 Ом, то это дает напряжение.

В этом задании вам нужно только заменить буквы на их значения и вычислить. U = 2 — 10 = 20 V.

Есть и более сложные задачи. Например:

Площадь четырехугольника вычисляется по следующей формуле: S = 1/2 d₁d₂Сина. Где d₁и г₂— диагонали четырехугольника, a — угол между ними. Вычислите Sinα. S = 21, d₁= 7, d₂= 15.

Сначала укажите количество, которое необходимо рассчитать (т.е. это количество и другие количества должны быть разделены знаком равенства). Для этого необходимо удалить дополнительные значения вокруг Sinα.

Да, я не знаю, как на это ответить. И поэтому я хочу не только понимать, но и любить. Как интересна математика, как в огромной шахматной партии, где огромное количество различных фигур, где само поле изгибается, ломается, закручивается в невообразимые узлы. Где так много интересных вопросов и проблем, что даже простые числа вдруг становятся такими непокорными и веками не дают спать лучшим математикам мира. И вы сможете научиться, если не будете получать готовые формулы, а попытаетесь сами вывести их из более простых. Вот простой пример: 65^2, как считать. Оказывается, все просто: умножьте 6 на (6+1), получите 42 и прибавьте 25, что даст вам ответ 4225. Таким образом, вы можете возвести в квадрат любое двузначное число, которое оканчивается на пять. И таких примеров можно привести множество. Если у вас есть интерес к этой великой науке. Да, из него получился бы хороший наставник, медленно открывающий маленькие таинственные двери в потусторонние лабиринты фантастических математических формул. Ведь за каждой формулой порой стоят долгие годы кропотливой работы. Голландец Людольф, например, насчитал 35 правильных цифр числа Пи(3,1415…)! И без калькулятора!!!!

В математике нет ничего, что можно было бы понять. Это своего рода аксиоматическая наука. При решении примеров и задач нужно проявлять смекалку. Но есть только один способ: нужно решать проблемы, чтобы научиться их решать. В школе у меня был уникальный учитель математики. Он привел такие примеры: из числа так и так…. до конца абзаца, сколько хватит. И вы должны понимать науку: Физика, химия, биология.

У меня сложные отношения с математическим анализом: с одной стороны, он показывает всю красоту и мощь математики, с другой — муки математического образования.

Математический анализ связывает различные предметы элегантным, но довольно сложным для ума способом. Ближайшая аналогия, которая приходит на ум, — это дарвиновская теория эволюции: как только вы понимаете ее, вы видите весь мир с точки зрения выживания. Понятно, почему лекарства приводят к появлению устойчивых микробов (выживание сильнейших). Вы понимаете, почему сахар и жир сладкие на вкус (вкус стимулирует потребление высококалорийной пищи, когда резервы организма невелики). Все эти моменты складываются в единую, логичную картину.

Таким же образом математический анализ освещает всю систему математики. Не кажется ли вам, что все эти формулы как-то связаны между собой?

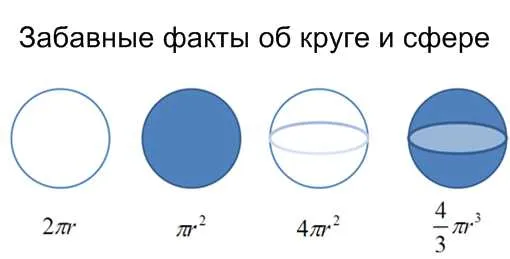
К ним относятся. Но большинство из нас изучают эти формулы самостоятельно. Математический анализ позволяет начать с «окружность = 2 * p * r» и экстраполировать другие формулы для вычисления площади круга, сферы и даже объема сферы — древним грекам такой подход был бы очень полезен.

К сожалению, математический анализ является воплощением всех трудностей в изучении математики. Большинство уроков объясняется с помощью надуманных, неправдоподобных примеров, непонятных доказательств и банального заучивания, которое полностью убивает интуицию.

Так не должно быть.

Математика, искусство и идеи

То, чему я научился в школе: Математика — это не самое сложное в математике; самое сложное — это мотивация для ее изучения. Прежде всего, умение не терять энтузиазма, несмотря ни на что:

• Преподавателей, больше сконцентрированных на штамповке публикаций и своей карьере, чем на преподавании
• Небеспочвенные опасения, что математика — это сложно, скучно, непопулярно или «не ваш предмет»
• Учебники и учебные планы, больше нацеленные на получение прибыли и хорошую статистику по тестированиям знаний, чем на пояснение сущности предмета.

«Плачущий математик» (pdf) — отличное эссе на эту тему, которое нашло отклик у многих, кто его прочитал:

«…если бы мне пришлось изобрести механизм с единственной целью уничтожить природное любопытство ребенка и его любовь к моделированию, я вряд ли смог бы сделать лучше того, что уже достигнуто — у меня просто не хватило бы воображения взяться за такие бесчувственные, тупые идеи, которые воплощены в современных методах преподавания математики».

Представьте себе изучение изобразительного искусства следующим образом: Дети, не рисуйте в детском саду. Вместо этого мы должны изучать химию цветов, физику света и анатомию глаза. Если после 12 лет изучения этих аспектов дети (или, скорее, подростки) все еще не против искусства, они могут начать рисовать сами. Наконец, у них есть полная основа для того, чтобы начать заниматься искусством. Верно?

То же самое относится и к поэзии. Представьте, что вы изучаете этот текст (формулу):

«Но главное — быть верным самому себе; тогда ты не будешь неверен другим, как день следует за ночью». -Уильям Шекспир, Гамлет

Это элегантный способ сказать: «Будь собой» (и если это означает писать о математике непочтительно, то так тому и быть). Но если бы мы изучали поэзию на уроке математики, мы бы не искали смысл, мы бы считали количество слогов, анализировали ямбический пентаметр и отмечали существительные, глаголы и прилагательные.

Как научиться понимать математику? | Учебный блог

Алгебра, геометрия, высшая математика…. Эти слова заставляют некоторых людей нервно грызть ногти и пригибать голову. Да, математика требует серьезного подхода и усилий, но не только умений.

Проблема в том, что у многих людей математика ассоциируется с такими понятиями, как дипломная работа, курсовая работа, тесты, контрольные работы и другие формы отчетности. К счастью, сегодня это совсем не проблема, потому что есть такие сайты, как 5orka.ru, которые помогут вам с такими работами. Очень важно любить математику.

Это постоянная работа и интересные упражнения, которые превращают математику в чистое удовольствие с интересными задачами и примерами. Вам не нужно запоминать формулы и наборы аксиом, не понимая их; они закрепляются в вашей памяти с помощью упражнений на развитие математического мышления.

Почему не все могут понять математику?

Для студентов с гуманитарным образованием изучение математики может стать кошмаром. Это связано с непониманием природы математических законов. Что вы тогда делаете? Как можно постичь все тайны математического мира, если желание изучать эту науку пропало?

Первые шаги к пониманию математики

Чтобы научиться понимать математику, мы должны изучать эту науку заново. Да, вам нужно заново выучить все формулы и изначальные законы, с пониманием и способностью объяснить их своими словами. Таким образом, у вас будет хорошая математическая база, которая поможет вам в дальнейшем обучении и погружении в мир математики. Спрашивайте своих учителей или репетиторов, если вам что-то непонятно, потому что откладывание непонятного материала может привести к плачевным последствиям, как снежный ком, катящийся по снегу и набирающий все больше и больше снега.

Научиться понимать, как решать математические задачи

Не менее важными для изучения математики являются способы решения математических задач. Они бывают всевозможных форм: обратные, инверсные, индуктивные…. Но вы не можете использовать их, если не понимаете метод. Поэтому сначала необходимо ознакомиться с основными методами, понять и освоить их, а также научиться их использовать. Для этого нужно посмотреть на готовые задания в учебниках и решить их логически.

Чтобы научиться понимать математику, нужно пытаться найти решение задачи по-своему, а не по шаблону. В конце концов, каждая проблема требует своего подхода и решения. Даже Евклид, основатель геометрии, говорил, что математика не знает королевской дороги. Это означает, что для решения задач и понимания мира математики нужен только ум и ничего больше. Кроме того, вы можете решать задачи с помощью формул простых чисел и логического мышления.

Например, вы можете не ставить перед квадратом двузначное число с цифрой 5 на конце, а использовать специально выведенную формулу. Например, число 65. Сначала прибавьте к первой цифре 1, а затем умножьте эту первую цифру на полученное число: 6 * (6 + 1) = 42. Итак, у нас есть 42, к которым мы прибавляем 25, и получается 4225, то есть 65 в квадрате!

Конечно, изучение математики требует не только собственных усилий, но и советов экспертов. В этом случае вы можете обратиться за помощью к репетитору или воспользоваться онлайн-помощью талантливых математиков через программы-мессенджеры.

Так что все в ваших руках! Помните об этом и добивайтесь своей цели!

Следить за почерком

Первая часть ЕГЭ контролируется машиной, которая преобразует ваш почерк в соответствующие символы. И будет очень обидно, если он случайно узнает другого персонажа. Чтобы избежать этих рисков, обратите внимание на свой почерк при написании теста. Не выходите за пределы коробки. Не пишите более одного символа в поле. Обязательно обратите внимание на шрифт:

Потренируйтесь заполнять бланки дома, чтобы не попасть впросак на экзамене. Энтузиазм, время, случайность — все это влияет на написание.

Но проблема не только в первой части. Даже если вторую часть проверяет один человек, это не меняет того факта, что вы можете получить более низкую оценку — если экзаменатор не понимает, что написано в тексте. Помните, что у экзаменатора есть десятки других работ, кроме вашей. Он не сядет за стол, чтобы понять, что такое цифра или буква. Еще один совет: рисунки тоже лучше делать аккуратно и не «клеить» буквы и знаки друг на друга.

Научиться работать с чертежом

У каждого ученика в то или иное время были проблемы с геометрией. Если в планиметрии все кажется не таким уж сложным, то переход к стереометрии происходит иначе, ведь здесь мы делаем объемный чертеж плана. Трудности возникают из-за того, что вершины, то есть стороны лица в нашей трехмерной фигуре, расположены неправильно. Например:

Согласитесь ли вы, что на втором рисунке удобнее работать с диагональным МК? Не волнуйтесь, если у вас не получается сразу сделать хороший рисунок: Сначала можно поискать лучший рисунок в черновом варианте (и желательно предварительно потренироваться на нем).

Как же выбрать положение вершин? Все отрезки и вершины, необходимые для решения, должны быть хорошо видны. Если в проблеме есть сегмент, он должен «развернуться» в нашу сторону. Края оснований должны быть нарисованы сбоку, чтобы их было легче увидеть. Если вам трудно понять рисунок, попробуйте изменить вершины! Хороший рисунок — залог успеха при решении стереометрических задач!

Первая часть — наше всё

Упражнения первой части намного легче, чем упражнения второй части. Поэтому рекомендуется сосредоточиться на них: Легче решить два упражнения из первой части, чем одно из второй (и вы получите одинаковый балл). В 2023 году по математике профиля ЕГЭ можно будет получить до 11 первичных баллов, то есть до 64 вторичных баллов только из первой части. Но помните, что набрать очки здесь так же легко, как и потерять их. Без 80% правильных ответов в первой части вторая часть теряет смысл.

Мы надеемся, что эти советы помогут вам подготовиться к JMU и сделать их легче! А чтобы подготовиться к экзамену без стресса, запишитесь на бесплатный пробный курс в онлайн-школе Tetrica. Репетиторы школы объясняют сложные темы простым языком и ведут вас к отличному результату. Удачи на экзамене!

Иллюстрация.

Реклама. Рекламодатель.

Формулы — одно из самых важных понятий в математике. Основные формулы облегчают вычисления и экономят время при решении уравнений. Давайте поговорим о том, что такое формула, откуда она берется и выделим основные формулы в математике.

Формула — это всегда уравнение. В левой части находится выражение, которое может быть преобразовано, а в правой — результат преобразования. При правильном использовании формулы многие шаги можно пропустить без потери правильного результата.

Формулу можно использовать в обоих направлениях. В геометрии это называется обратным действием, но чаще это просто называют коллапсом. Если выражение в левой части формулы преобразуется в выражение в правой части, то говорят, что оно свернуто формулой. В противоположном случае она расширяется.

Давайте рассмотрим пример. Используйте формулу для суммы квадратов: $(a+b)^2=a^2+2*ab+b^2$.

У нас есть следующее выражение: $(2a+7b)^2=(2a)^2+2*(2a)*(7b)+(7b)^2=4a^2+28aβ+49b^2$ — поэтому мы раскрыли скобки с формулой суммы квадратов. Если нам нужно преобразовать конечное выражение в исходное, то это будет обратная формула.

Основными формулами в математике являются формулы быстрого умножения. Их не так много, поэтому лучше всего выучить их все наизусть. Всего существует семь формул, и каждая из них предназначена для облегчения подсчета. Формулы изучаются в четыре этапа.

• Первыми идут формулы суммы и разности квадратов. Формулу суммы мы уже знаем.

• $(a+b)^2=a^2+2ab+b^2$
• Квадрат разности не сильно отличается.
• $(a-b)^2=a^2-2ab+b^2$
• Знак минуса вполне логичен, и его достаточно просто запомнить.

• Следующими запоминают куб суммы и куб разности. Они учатся быстрее, просто запоминаясь по аналогии.

• Дальше идут формулы суммы и разности кубов, а так же разность квадратов. Разность квадратов записывается достаточно легко.

$a^2+b^2=(a+b)(a-b)$ — но формулы для суммы квадратов не существует. В начале урока математики в 5 классе ученики часто путаются в формулах для квадрата разности и разности квадратов. Давайте попробуем научиться различать их.

В чем разница между квадратами? Это два числа в квадрате, одно из которых вычитается из другого. А каков квадрат разницы? Одно число вычитается из другого, а результат возводится в квадрат. Запомните и поймите это объяснение один раз, и больше никогда не возникнет проблем с этими двумя формулами.

• Следующими и последними идут формулы суммы и разности кубов. Они немного сложнее и для облегчения их запоминания придумали понятие неполного квадрата суммы и неполного квадрата разности.

1. Вспомним формулу квадрата суммы.
2. $(a+b)^2=a^2+2ab+b^2$
3. Обратим внимание на вторую часть.
4. $a^2+2ab+b^2$ – это и называется полным квадратом суммы. А неполным называется выражение:

$a^2+ab+b^2$. Это легко запомнить. По аналогии, несовершенный квадрат разности: $a^2-ab+b^2$.

• Теперь приведем формулы суммы и разности кубов.
• $a^3+b^3=(a+b)( a^2-ab+b^2)$ – сумма кубов это произведение суммы чисел на неполный квадрат разности этих чисел.
• $a^3+b^3=(a-b)( a^2+ab+b^2)$ – разность кубов это произведение разности чисел на квадрат суммы этих чисел.

Практика показывает, что последние две формулы легче запомнить в словесной форме. Более того, эти формулы часто используются при решении простых уравнений. Поэтому, чтобы не бегать каждый раз в интернет, проще выучить их наизусть.

Основные математические формулы

Образование — это то, что остается после того, как вы забыли все, чему вас учили в школе.

Игорь Хмелинский, ученый из Новосибирска, работающий сейчас в Португалии, доказывает, что трудно развить абстрактную память у детей без непосредственного заучивания текстов и формул. Вот выдержки из его статьи «Уроки реформ образования в Европе и бывшем Советском Союзе».

Незнание таблицы умножения имеет более серьезные последствия, чем неспособность распознать ошибки при вычислениях с помощью калькулятора.

Наша долговременная память работает по принципу ассоциативной базы данных, т.е. когда мы вспоминаем определенную информацию, она связывается с другой информацией на основе ассоциаций, возникших, когда мы ее знали.

Поэтому, чтобы создать базу знаний по какому-либо предмету, например, по арифметике, необходимо хотя бы что-то запомнить.

Более того, новая информация переходит из кратковременной памяти в долговременную, когда мы сталкиваемся с ней неоднократно в течение короткого периода времени (несколько дней) и желательно в разных контекстах (что помогает создать полезные ассоциации).

Однако, поскольку знания из арифметики не хранятся постоянно, вновь приобретенная информация ассоциируется с вещами, не имеющими отношения к арифметике, например, с личностью учителя, погодой за пределами школы и т.д.

Очевидно, что такое заучивание не приносит реальной пользы ученику — поскольку ассоциации удалены из конкретной предметной области, ученик не может вспомнить никаких знаний, связанных с арифметикой, кроме смутного представления о том, что когда-то он должен был что-то слышать об этом. Для таких студентов роль недостающих связей обычно играют различного рода подсказки — копирование у коллеги, использование наводящих вопросов в самом тесте, формулы из списка допустимых формул и т.д. В реальной жизни такой человек совершенно беспомощен без подсказок и не способен применить те знания, которые у него есть в голове.

Формирование математического аппарата происходит медленнее, чем обычно, если формулы не выучены наизусть. Почему? Во-первых, новые свойства, теоремы и отношения между математическими объектами почти всегда используют некоторые особенности ранее изученных формул и понятий.

Будет труднее сконцентрироваться на новом материале, если эти характеристики не могут быть вызваны из памяти в течение короткого времени.

Во-вторых, если не знать формулы наизусть, трудно найти решения важных задач, включающих большое количество мелких операций, в которых нужно не только выполнить определенные преобразования, но и определить порядок этих операций, заранее проанализировав применение многих формул в два-три этапа.

Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его когнитивных основ и способностей, происходит гораздо быстрее, когда большая часть используемой информации (свойства и формулы) присутствует в голове ребенка. Чем стабильнее и чем дольше он там хранится, тем лучше.

НУЖНЫ ЛИ ВАМ ЕЩЕ ДОКАЗАТЕЛЬСТВА ТОГО, ЧТО ВЫ ДОЛЖНЫ ВЫУЧИТЬ ФОРМУЛЫ НАИЗУСТЬ?

Все формулы по математике — Формулы под рукой

Не можете решить проблему? Наш сайт поможет вам учиться и готовиться к сложным экзаменам, тестам, олимпиадам, встречам и ЕГЭ.

Лауреат премии Эйнштейна, знаменитый британский исследователь теоретической физики Стивен Хокинг, однажды сказал, что устроился на работу профессором математики в Оксфордский университет без специальной подготовки.

В то время он обладал лишь зачаточными знаниями в области математики. Он постигал царицу наук «на ходу», читая студенческий учебник на две недели раньше срока.

Впоследствии студенты Хокинга находили его уроки чрезвычайно познавательными и увлекательными!

Такие примеры вдохновляют и вселяют веру в то, что каждый из нас мог бы подтянуть знания о «забытом». И тогда возникнет новое агентство по развитию.

Чтобы вам было легче запомнить (или выучить!) учебную программу, мы рекомендуем вам не листать учебники и справочники, а воспользоваться нашим сайтом, где вы сможете быстро найти нужную формулу по вашему предмету благодаря практичной навигации и поисковой системе:

• арифметика;
• алгебра;
• геометрия;
• физика;
• химия.

От теории к практике

Бывает, что материал известен, и даже формулы, теоремы и аксиомы по нужному предмету — вот они, но работа недоступна. Педагогический «диагноз»: нет опыта. Этот опыт приобретается путем решения формальных уравнений и задач. Мы предлагаем самые успешные и интуитивно понятные методики, которые помогли не одному студенту овладеть инструментами точных наук!

Быстрее, выше, сильнее!

Сейчас вы можете подумать, что невозможно выучить все формулы в школе. На самом деле, для решения задач по математике школьного уровня вам понадобится не более двухсот формул, а по физике и того меньше! Это означает, что вы можете постепенно запомнить все основные формулы, просматривая наши учебники и осваивая принципы решения формальных задач!

Какими бы сложными ни казались сейчас задачи ваших учителей, в какой-то момент стены вашей школы или университета покажутся вам слишком узкими.

На этом сайте вы найдете коллекцию формул, которые настолько же просты в использовании, насколько сложны. Если вы хотите узнать больше, чем написано в учебнике, начните с аксиомы — слов Марка Твена, который сказал: «Никогда не позволяйте школьной работе мешать образованию!».