Компьютерными веб-сайтами может пользоваться любой человек, имеющий подключение к Интернету и веб-браузер с поддержкой Flash. Для сервисов, предлагающих данный вид услуг, не требуется регистрация или предоставление персональных данных. Система рассчитывает ответ автоматически.
Формула пути
Линия, которую материальная точка описывает при движении, называется траекторией.
Длина траектории — это сумма длин всех отрезков траектории, пройденных точкой за промежуток времени от t до t.1к2.
Когда уравнения движения представлены в декартовой прямоугольной системе координат, длина пути (s) определяется следующим образом:
В цилиндрических координатах длина пути может быть выражена следующим образом:
Напишите формулу для длины пути в сферических координатах:
Положение движущейся материальной точки в фиксированный момент времени, например, t=t1называется начальной позицией. Очень часто предполагается, что t1=0. Длина пути, который проходит материальная точка от своего начального положения, является скалярной функцией времени: s=s(t).
Предполагается, что материальная точка проходит расстояние ds за промежуток времени $d t
ightarrow 0$, которое называется элементарным расстоянием. В данном случае:
Виды движения и формулы длины пути
Здесь $\bar$ — вектор элементарного движения материальной точки, v — мера ее скорости.
Длина пути при равномерном движении (v=const) точки равна:1где t2— контрольное начало движения, t
— это конец системы отсчета. Формула (5) показывает, что расстояние, пройденное равномерно движущейся материальной точкой, является линейной функцией времени.
Если движение неравномерное, то длина пути $\Delta s$ в интервале времени от $t$ до $t + \Delta t$ может быть определена следующим образом:
$\Delta s=\угольник v\диагональ \Delta t(6)$
где $\langle v
angle$ — средняя скорость движения. Для равномерного движения $\угольник v\угольник = v$ .0Расстояние, пройденное материальной осью при равномерном движении (a=const), рассчитывается следующим образом:
Единицы измерения пути
Где a — постоянное ускорение, v
— начальная скорость движения.
Основной единицей измерения расстояния в системе СИ является: s=m
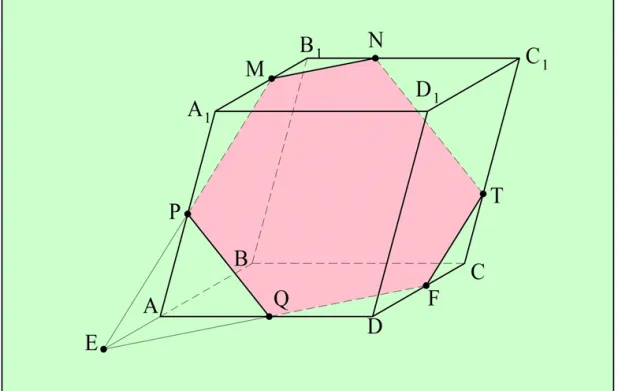
Задание. Траектория движущейся точки показана на рисунке 1. Какое расстояние проходит точка и каково ее перемещение при движении точки 1-2-3-4.
Решение. Смещение — кратчайшее расстояние между точками 1 и 4. Следовательно, смещение точки одинаково:
Path — длина пути. Рассматривая диаграмму на рисунке 1, мы видим, что путь материальной точки равен:
Реакция. Длина пути составляет 20 м, а смещение — 4 м.
Проверенные авторы готовы помочь вам написать работу любой сложности
Мы уже помогли 4 396 студентам и школьникам справиться с заданиями от решения задач до магистерской диссертации! Определите стоимость вашего задания за 15 минут!
Задание. Уравнение движения материальной точки в декартовой прямоугольной системе координат представлено функцией: x=-0,2t 2 (м). Какое расстояние проходит материальная точка за 5 секунд?
Решение. Поскольку уравнение движения задается одной координатой, за основу решения задачи о форме мы возьмем формулу пути:
Задачи на встречное движение
Подставляя в (2.1) функцию x=-0.2t 2, получаем, что поскольку c \leq t \leq 5 c$:Ответ. s=5м.В этих задачах два объекта движутся навстречу друг другу. Задачи на встречное движение можно решить двумя способами: 1. Найдите значения скорости, времени и расстояния для каждого объекта. 2. найти скорость, расстояние, время и расстояние до объекта.
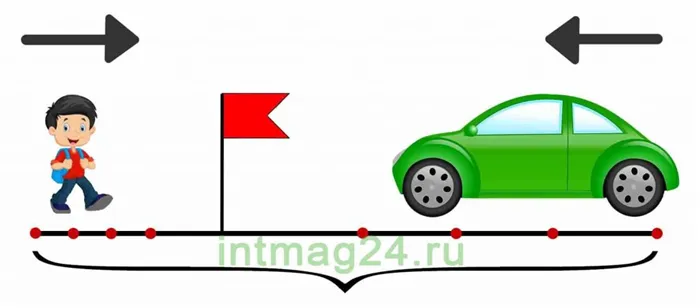
Скорость приближения, скорость, время, расстояние, скорость, расстояние, расстояние, расстояние, время и расстояние до объекта.
объектов (как сумма их скоростей), общее время и расстояние. Скорость сближения — это расстояние, которое два объекта проходят друг до друга за единицу времени.
Задание 4.
Два поезда отправились из двух пунктов, чтобы встретиться в одно и то же время, и встретились через 3 часа. Первый поезд двигался со скоростью 80 км/ч, второй — 70 км/ч. На каком расстоянии друг от друга находятся точки? Решение: Первый способ. Найдите расстояние, пройденное каждым автобусом, и сложите данные: 80*3=240 (км) — проехал первый автобус, 70*3=210 (км) — проехал второй поезд, 240+210=450 (км) — проехали два поезда. Второй способ. Найдите скорость сближения поездов, т.е. на сколько уменьшается расстояние между ними в час, а затем найдите расстояние: 80+70=150 (км/ч), 150*3=450 (км). Ответ: Расстояние между двумя городами составляет 450 км.
Задачи на движение в противоположных направлениях
450 450 километров, или 450 450 км.Два автобуса выехали из двух городов, чтобы встретиться в одно и то же время. Первый автобус ехал со скоростью 80 км в час, а второй — 70 км в час. Два автобуса встретились в одно и то же время. Каково расстояние между ними за 2 часа, если расстояние между городами 450 км. Решение. Сколько километров проехал каждый автобус, и найти оставшееся расстояние: 80*2=160 (км) — проехал первый автобус, 70*2=140 (км) — проехал второй автобус, 160+140=300 (км) — проехали оба автобуса, 450-300=150 (км) — еще осталось. Второй способ. Найдите скорость сближения автобусов и умножьте ее на время в пути. 80*70=150 (км/ч) — скорость сближения; 150*2=300 (км) — два автобуса проехали; 450-300=150 (км) — еще предстоит проехать. Ответ: Через 2 часа расстояние между автобусами составит 150 км.В таких задачах два объекта движутся в противоположных направлениях и удаляются друг от друга. В этом типе проблем используется следующее
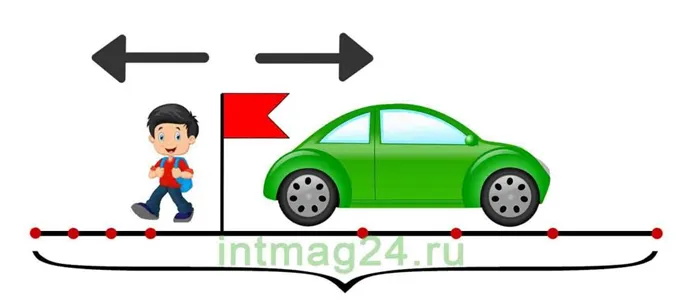
Скорость разделения
. Задачи на движение в противоположных направлениях также могут быть решены двумя способами: 1. Найдите значения скорости, времени и расстояния для каждого объекта. 2. найти скорость разделения объектов (как сумму их скоростей), общее время и расстояние. Скорость разделения — это расстояние в единицу времени, которое увеличивается между двумя объектами, движущимися в противоположных направлениях.
Проблема 6.
Два автомобиля выехали из одной точки в одно и то же время в противоположных направлениях. Скорость первого автомобиля 100 км/ч, а скорость второго автомобиля 70 км/ч. Каким будет расстояние между автомобилями через 4 часа? Решение: первый метод. Найдите расстояние, пройденное каждым автомобилем, и сложите результаты: 1) 100 — 4 = 400 (км) — проехал первый автомобиль 2) 70 — 4 = 280 (км) — проехал второй автомобиль 400 + 280 = 680 (км) Второй метод. Найдите скорость разделения, т.е. величину увеличения расстояния между автомобилями в час, а затем умножьте скорость разделения на время движения. 100 + 70 = 170 км/ч — это скорость, с которой автомобили разъезжаются. 170 — 4 = 680 (км) Ответ: 680 км пройдено между автомобилями за 4 часа.
Задачи на движение в одном направлении
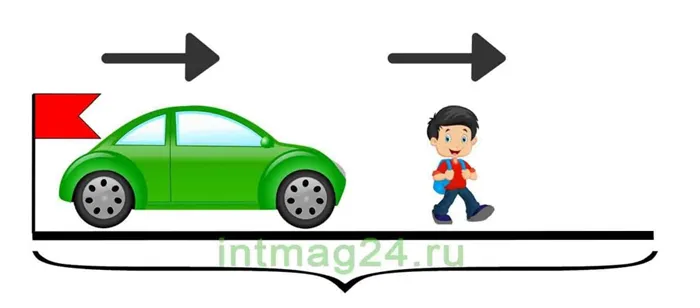
Задание 7.Два туриста шли в противоположных направлениях из двух населенных пунктов, расположенных в 40 км друг от друга. Первый участник шел со скоростью 4 км/ч, а второй — со скоростью 5 км/ч. Каково расстояние между участниками похода через 5 часов? Решение. Найдите, сколько километров прошел каждый из туристов за 5 часов, сложите полученные результаты, а затем прибавьте к полученному расстоянию расстояние между населенными пунктами. 1) 4 — 5 = 20 (км) — пройдено первым туристом. 2) 5 — 5 = 25 (км) — прошел второй турист. 3) 20 + 25 = 45 (км). 4) 45 + 40 = 85 (км). Вторая прогулка. Найдите скорость ходьбы пешеходов, затем пройденное расстояние и прибавьте к результату расстояние между населенными пунктами. 4 + 5 = 9 (км/ч); 9 — 5 = 45 (км); 45 + 40 = 85 (км)? Ответ: Через 5 часов расстояние между пешеходами составит 85 км.В этих задачах два объекта движутся в одном направлении с разными скоростями, в то время какПодходмежду ними илиОтвет. s=5м.друг от друга. Следовательно, мы находимДва автобуса выехали из двух городов, чтобы встретиться в одно и то же время. Первый автобус ехал со скоростью 80 км в час, а второй — 70 км в час. Два автобуса встретились в одно и то же время. Каково расстояние между ними за 2 часа, если расстояние между городами 450 км. Решение. Сколько километров проехал каждый автобус, и найти оставшееся расстояние: 80*2=160 (км) — проехал первый автобус, 70*2=140 (км) — проехал второй автобус, 160+140=300 (км) — проехали оба автобуса, 450-300=150 (км) — еще осталось. Второй способ. Найдите скорость сближения автобусов и умножьте ее на время в пути. 80*70=150 (км/ч) — скорость сближения; 150*2=300 (км) — два автобуса проехали; 450-300=150 (км) — еще предстоит проехать. Ответ: Через 2 часа расстояние между автобусами составит 150 км.ή
скорость передвижения
Объекты.
Формула для нахождения скорости сближения или разделения двух объектов, движущихся в одном направлении: Вычтите меньшую скорость из большей скорости.
Проблема 8.
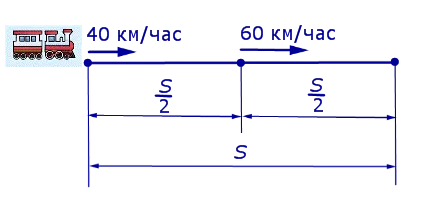
Автомобиль выезжает из города со скоростью 40 км/ч. Через 4 часа второй автомобиль следует за ним со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый? Решение. В этом случае скорость первого автомобиля составляет 40 км/ч, а время в пути на 4 часа больше, чем у второго автомобиля (или t+4). Скорость второго автомобиля 60 км/ч, время в пути t. Расстояние, пройденное обоими вагонами, одинаково. Поэтому мы можем сформулировать уравнение: 40*(t+4)=60*t. Это дает t=8 (часов), т.е. время, которое требуется второму автомобилю, чтобы добраться до первого. Решите задачу без использования уравнения. Таким образом, когда второй автомобиль выехал из города, первый автомобиль был в пути уже 4 часа: 40 — 4 = 160 (км). Второй автомобиль едет быстрее первого, поэтому каждый час расстояние между автомобилями уменьшается на разницу их скоростей: 60 — 40 = 20 (км/ч) — это скорость сближения. Разделите расстояние между автомобилями на скорость их сближения, чтобы узнать, через сколько часов они встретятся: 160 : 20 = 8 (h) Ответ: Второй автомобиль догонит первый через 8 часов.
Проблема 9.
Два пешехода одновременно вышли из двух населенных пунктов на расстоянии 5 км в одном направлении. Скорость пешехода впереди — 4 км/ч, а скорость пешехода сзади — 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого? Решение: Поскольку второй пешеход движется быстрее первого, расстояние между ними уменьшается с каждым часом. Поэтому мы можем определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч). Оба пешехода отправились в путь одновременно, поэтому расстояние между ними равно расстоянию между деревнями (5 км). Если разделить расстояние между ними на скорость их сближения, то получится, через сколько времени второй пешеход догнал бы первого: 5 : 1 = 5 (h) Ответ: Через 5 часов второй пешеход догнал бы первого.
ГДЗ учебник по математике 3 класс Петерсон. 2 урок. Формула пути. Номер №5
Реши задачи по формуле пути s = v * t. а) Всадник едет на лошади со скоростью 8 км/ч. Какое расстояние он пройдет за 4 часа?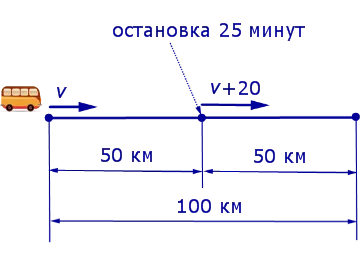
б) Чему равна скорость почтового голубя, если за 2 ч он пролетает 120 км?
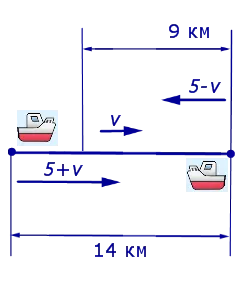в) Пчела летит со скоростью 6 м/с. За какое время она долетит до улья, если находится на расстоянии 360 м от него?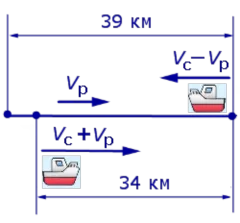
Решение б
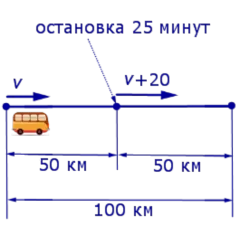
Проблема 10.
Два автомобиля выехали из одного места в одно и то же время в одном и том же направлении. Скорость первого автомобиля 80 км/ч, а второго — 40 км/ч. 1) Какова скорость на расстоянии между двумя автомобилями? 2) Каким будет расстояние между автомобилями через 3 часа? 3) Через сколько часов расстояние между ними составит 200 км? Решение: 1) 80 — 40 = 40 (км/ч) — это скорость автомобилей, удаляющихся друг от друга. 2) 40 — 3 = 120 (км) — это расстояние между ними за 3 часа; 3) 200 : 40 = 5 (ч) — это время, за которое расстояние между машинами составит 200 км. Реакция. 3) Через 5 часов расстояние между автомобилями составит 200 км.
