Предмет стереометрии. Стереометрия это часть геометрии которая изучает.

Содержание

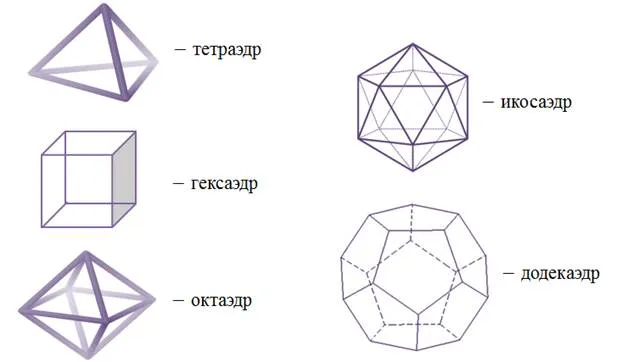
Треугольная пирамида называется тетраэдром, если все ее грани — равные правильные треугольники. Тетраэдр — это частный случай правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида является тетраэдром).

Геометрия вокруг нас. Геометрия вокруг нас: основные разделы геометрии

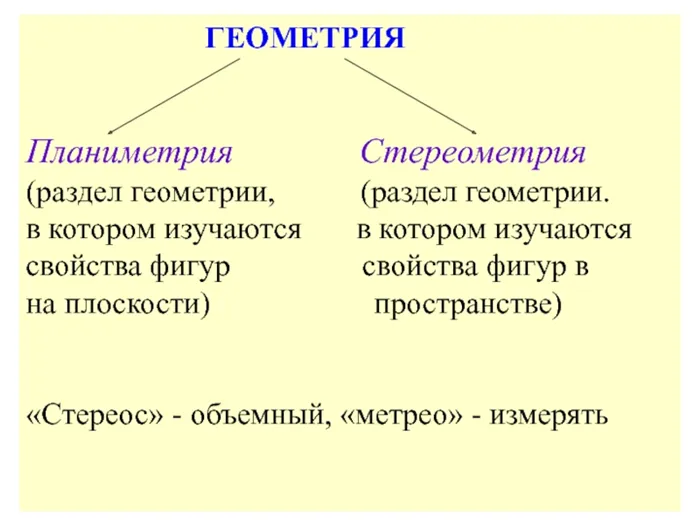
Стереометрия — это раздел геометрии, изучающий свойства фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «stereos» — объемный, пространственный и «metreo» — измерять.

Простейшие формы в пространстве: точка, линия, плоскость.

Самолет. Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическая фигура должна быть представлена как бесконечно простирающаяся во всех направлениях.

На чертежах плоскость изображается как параллелограмм или как любая поверхность и обозначается греческими буквами a, b, c и так далее. Точки A и B лежат на плоскости b (плоскость b проходит через эти точки), а точки M, N и P не лежат на этой плоскости. Вкратце это можно сформулировать следующим образом: A ∈ β, B ∈ β,

Аксиомы стереометрии и их следствия

Аксиома 1. Все три точки, не лежащие на одной прямой, имеют плоскость, пересекающую их, и только одну из них.

Аксиома 2: Если две точки на прямой лежат в плоскости, то все точки на прямой лежат в этой плоскости. (Линия лежит на плоскости или плоскость проходит через линию).

Из Аксиомы 2 следует, что прямая, не лежащая в данной плоскости, имеет с ней не более одной общей точки. Если прямая и плоскость имеют общую точку, то они пересекаются.

В этом случае плоскости пересекаются на прямой линии.

Пример: пересечение двух смежных стен, стена и потолок комнаты.

Некоторые выводы из аксиом

Теорема 1. Плоскость проходит через прямую a и точку A, которая на ней не лежит, и только через одну.

Теорема 2. Две пересекающиеся прямые a и b пересекаются только одной плоскостью.

Параллельные линии в пространстве

Две прямые в пространстве считаются параллельными, если они принадлежат одной плоскости и не пересекаются.

Теорема о параллельных прямых.

Прямая, параллельная данной прямой, проходит через любую точку пространства, но только через одну.

Лемма для пересечения плоскости параллельными прямыми. Если одна из двух параллельных прямых пересекает заданную плоскость, то другая параллельная прямая также пересекает эту плоскость.

Теорема о трех линиях в пространстве. Если две прямые параллельны третьей прямой, то они параллельны (если a ∥ c и b ∥ c, то a ∥ b ).

Параллельность прямой и плоскости

Прямая и плоскость считаются параллельными, если они не имеют общих точек.

Доказательство параллельности прямой и плоскости

Теорема. Если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она параллельна этой плоскости.

Теорема. Если плоскость проходит через заданную прямую, параллельную другой плоскости, и пересекает эту плоскость, то точка пересечения плоскостей параллельна заданной прямой.

Теорема. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Взаимное расположение линий в пространстве

Линии, которые пересекаются: лежат в одной плоскости, имеют общую точку.

Параллельные прямые: лежат в одной плоскости, не имеют общих точек (не пересекаются).

Стереометрия

Стереометрия (от греч. stereos — «твердый», «твердый, объемный, пространственный» и metreo — «измерять») — это раздел геометрии, изучающий свойства фигур в пространстве. Основными (простейшими) формами в пространстве являются точки, линии и плоскости. В стереометрии существует новый тип взаимного расположения линий: пересекающиеся линии. Это одно из немногих существенных различий между стереометрией и планиметрией, поскольку во многих случаях проблемы стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Этот раздел не следует путать с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), тогда как в стереометрии изучаются свойства фигур в пространстве (свойства пространственных фигур).

Аксиомы стереометрии

На каждой прямой и в каждой плоскости имеются по крайней мере две точки.
В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник

Многогранник — это твердое тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников — ребрами и вершинами многогранника соответственно. Полиэдры могут быть выпуклыми или невыпуклыми. Выпуклый многогранник лежит на той стороне плоскости, которая проходит через одно из его ребер.

Литература

В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
И. Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Выпуск 31).

Портал «Математика»
Категория «Математика»

Предмет стереометрии

На этом уроке учащиеся познакомятся с понятием стереометрии. Мы объясним основное различие между стереометрией и планиметрией. Мы рассмотрим историю развития геометрии. Мы рассмотрим основные фигуры, которые будем изучать позже.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из комплекта, вам нужно добавить его в свой личный шкафчик.

2. Распространите видеоуроки среди своих учеников в личных кабинетах.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Предмет стереометрии»

Мы занимаемся геометрией с третьего класса и почти всегда имеем дело с плоскими фигурами, т.е. фигурами, которые полностью лежат в плоскости. Раздел геометрии, который занимается изучением свойств плоских фигур, называется планиметрией. Основными элементами планиметрии являются точка и линия.

Плоские фигуры имеют только два измерения: длину и ширину. Эти измерения используются для определения площади фигуры.

Но давайте посмотрим вокруг. В природе практически не существует плоских тел. Все объекты расположены в пространстве и не помещаются в одну плоскость. Часть геометрии, изучающая свойства этих фигур, называется стереометрией.

Например, если в планетометрии мы говорим о квадрате, то в стереометрии мы говорим о кубе, состоящем из квадратов.

Если в планиметрии мы говорим о правильном треугольнике, то в стереометрии мы сделаем из треугольника конус, вращая его вокруг одного из зондов.

Слово стереометрия происходит от двух древнегреческих слов stereos — «твердый, пространственный» и metreo — «измерять». В отличие от планиметрии, основными элементами стереометрии являются точка, линия и плоскость.

Как и в планиметрии, точки обозначаются заглавными буквами латинского алфавита. Узкие места обозначаются строчными буквами латинского алфавита.

Плоскость может быть представлена различными способами, но чаще всего ее представляют в виде параллелограмма. Для обозначения плоскости используются строчные буквы греческого алфавита.

Помимо этих понятий, стереометрия имеет дело с геометрическими твердыми телами и их поверхностями. Геометрические тела имеют три измерения: длину, ширину и высоту. Эти измерения позволяют вычислить объем фигуры, т.е. геометрическое тело имеет емкость. Почти каждый объект, который нас окружает, может быть представлен в виде геометрического тела.

Тела, поверхности которых состоят из многоугольников, называются многогранниками.

Стереометрия, как и планетометрия, развивалась вместе с человеком. Геометрия была необходима строителям, которые возводили плотины на реках, мосты и виадуки с одного берега на другой, небоскребы и великолепные храмы.

Египетские пирамиды, построенные за два или четыре тысячелетия до нашей эры, являются хорошим примером. И по сей день эти пирамиды поражают нас точностью своих метрических пропорций.

Считается, что геометрия зародилась в Древнем Египте около 2000 года до нашей эры. В V веке нашей эры древнегреческий ученый Геродот написал следующее о происхождении геометрии: Египетский фараон Сеозострис разделил землю, выделив каждому египтянину участок земли и обложив каждый участок соответствующим налогом. Когда Нил затоплял тот или иной участок, жертва обращалась к царю, который посылал землемеров, чтобы определить, насколько уменьшился участок, и соответственно снижал налог. Таким образом, геометрия зародилась в Египте и распространилась оттуда в Грецию.

Геродот Галикарнасский (ок. 484 до н. э. — ок. 425 до н. э.)

Основные понятия стереометрии

Стереометрия работает со всеми терминами, которые мы знаем из планетометрии — точка, линия, круг, треугольник и т.д. Но помимо этих понятий существуют и другие.

Самым важным из основных понятий стереометрии является плоскость. В литературе иногда используется аббревиатура самолет. Плоскость не имеет строгого определения в геометрии, но считается основным понятием, как точка и линия в планетометрии. Только некоторые из его свойств задаются косвенно аксиомами. В реальной жизни примерами плоскости являются поверхность стола или лист бумаги. Однако, в отличие от них, плоскость не имеет границ, она бесконечна (как и прямая линия). Плоскость не имеет кривизны, например, поверхность сферы не является плоскостью. Когда плоскость изображают на чертежах, ее обычно показывают в виде параллелограмма и традиционно изображают маленькими буквами греческого алфавита, используемыми в планетометрии для обозначения углов (a, b, c и т.д.):

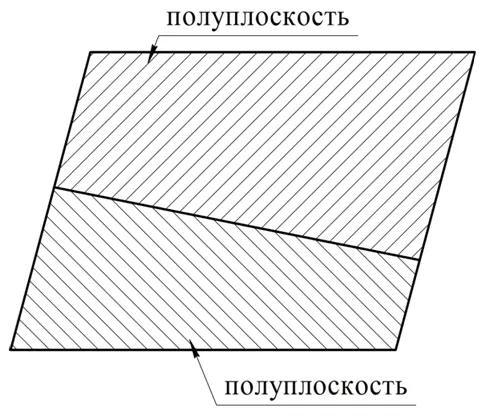
Когда на плоскости проводится линия, она делит ее на две фигуры, называемые полуплоскостями:

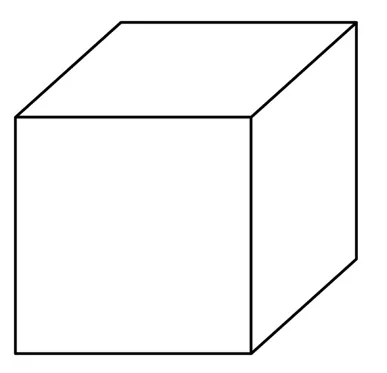
Объемные формы — это часть пространства, отделенная от остального пространства замкнутой поверхностью, т.е. границей. Самый простой пример объемной формы — куб:

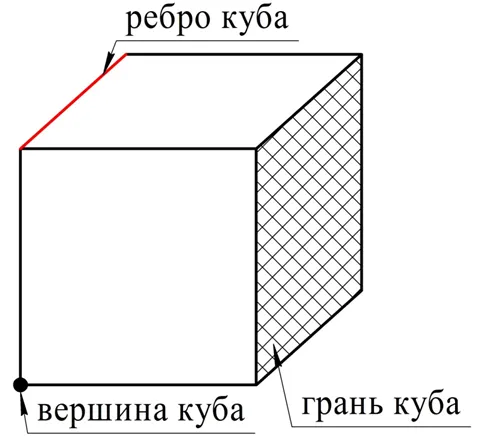
Поверхность куба состоит из 6 равных квадратов, каждый из которых является стороной куба. Стороны этих квадратов являются гранями куба, а вершины квадратов также являются вершинами куба.

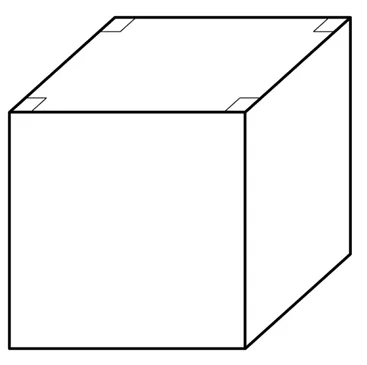
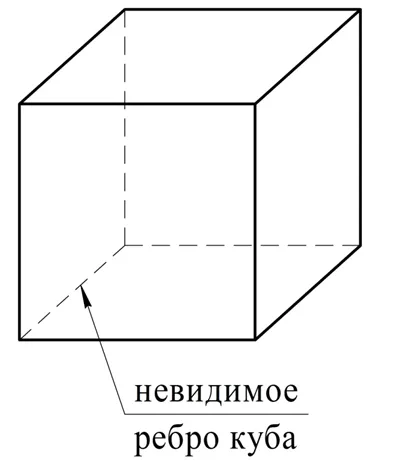
Посмотрите на изображение куба. Здесь он появляется немного сбоку, поэтому изображение становится трехмерным. Однако нам нужно исказить некоторые размеры и углы на чертеже. Например, верхняя грань должна быть квадратной, но на плоском чертеже углы этой грани неправильные. При необходимости мы просто ставим между сегментами специальный орфографический символ, который также используется в планиметрии:

Важно понимать, что из-за искажения размеров трехмерных форм на плоских чертежах мы НЕ можем проверить решение некоторых стереометрических задач с помощью точных построений. Однако существуют специальные компьютерные программы для 3D-рисования, которые уже сейчас можно использовать для создания таких конструкций. Обратите также внимание, что на рисунке показаны не все 6 граней куба, а только 3 из них. Если необходимо показать линии, которые не видны на чертеже, используются пунктирные линии:

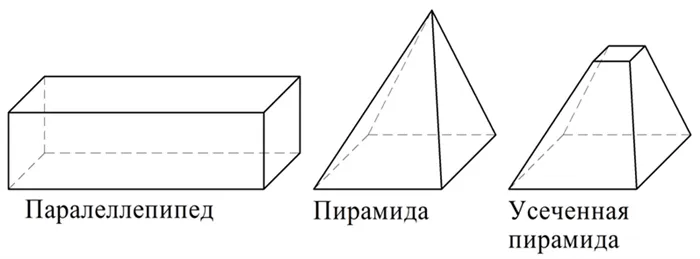
Все стороны куба являются многоугольниками. Если фигура состоит только из многоугольников на всей своей поверхности, она называется многогранником. Поэтому куб является примером многогранника. Другими примерами многогранников являются параллелепипед, пирамида и усеченная пирамида:

Ниже более подробно описаны различные типы многогранников и одновременно даны их определения.

Аксиомы стереометрии

Стереометрия, как и планетометрия, основана на некоторых фундаментальных положениях, которые считаются совершенно само собой разумеющимися и не требуют доказательств. Они называются аксиомами. Аксиомы используются для доказательства простейших теорем стереометрии, которые затем используются для доказательства других, более сложных теорем, и так далее. В общем, аксиомы — это первые, основные теоремы, которые принимаются без доказательства.

Аксиомы вместе образуют то, что называется аксиоматической системой или аксиоматикой. Аксиоматическая система должна быть когерентной, т.е. ее нельзя использовать для доказательства истинности и ложности одного и того же предложения одновременно. Он также должен быть независимым. Это означает, что ни одна из аксиом не может быть доказана с помощью других аксиом (иначе аксиому можно просто исключить из списка аксиом и считать теоремой). Наконец, аксиоматика должна быть полной, т.е. с ее помощью каждая теорема может быть либо доказана, либо опровергнута, и не должно быть недоказуемых теорем.

На самом деле, вопрос выбора аксиоматической системы в любой математической дисциплине, включая геометрию, довольно сложен. Первая аксиоматическая система была сформулирована еще Евклидом, но впоследствии оказалась не совсем удачной. Наиболее часто используемой аксиоматической системой является система Гильберта, которая была сформулирована в 1899 году. Однако помимо этой системы существует множество других аксиоматических систем: системы Погорелова, Колмогорова, Вейля, Биргофа и так далее.

Прежде чем сформулировать сами аксиомы, уточним, что существуют так называемые неопределенные термины стереометрии. В аксиоматике Гильберта это плоскость, точка и прямая. Их свойства точно описываются аксиомами. Остальные термины определены, многие из них сформулированы в 7-9 классах.

Всего в аксиоме Гильберта 20 аксиом. Из них 15 относятся к планиметрии и только 5 — к стереометрии. Сначала сформулируем две аксиомы для трех точек:

Поскольку здесь даны два разных утверждения, принято разделять их на две разные аксиомы. Для облегчения поиска их можно объединить в одно заявление:

Другими словами, любые три точки лежат в одной плоскости. По этой причине для обозначения плоскостей иногда указывают три точки (важно, чтобы они не принадлежали одной линии).

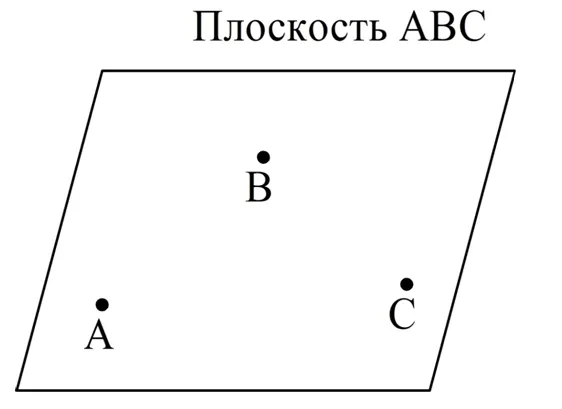
Иногда этот термин используется, чтобы сказать, что три точки однозначно определяют плоскость или однозначно определяют ее.

Случай, когда три точки лежат на одной прямой, рассматривается ниже отдельно.

Далее мы называем ее аксиомой четырех точек:

Три постулата стереометрии можно легко подтвердить примером из жизни. Возьмите стул с тремя ножками. Мы можем прочно поставить его на пол, даже если длина ножек не одинакова. Однако, если у стула 4 ножки, он иногда начинает «шататься» (если ножки разной длины). В трех местах она будет опираться на пол, а четвертая опора будет висеть в воздухе. Это связано с тем, что 4 конца ножек могут находиться на разных уровнях. Это невозможно для стула с тремя ножками, поскольку ножки всегда находятся в одной плоскости.

Простейшие следствия из аксиом стереометрии

На основе аксиом можно доказать некоторые простые теоремы стереометрии.

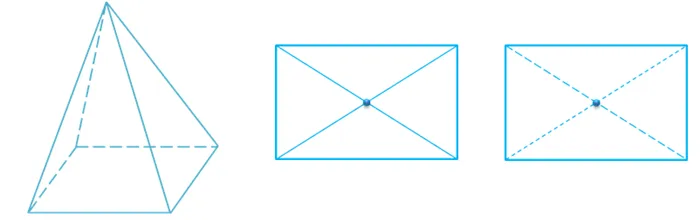
Доказательство. Возьмем любую прямую m и точку C, которая НЕ принадлежит m. Затем отметьте две любые точки на m и обозначьте их A и B:

По аксиоме 1 мы можем провести плоскость a через A, B, C. Согласно аксиоме 4, m принадлежит a. Таким образом, мы доказываем, что существует плоскость, проходящая через m и C. Единственность этой плоскости следует из Аксиомы 2, поскольку две разные плоскости не могут проходить через A, B, C и так далее.

Иногда доказанный факт выражается иначе: прямая и точка, не лежащая на прямой, однозначно определяют плоскость, проходящую через нее. Это означает, что если мы определяем линию и точку, то одновременно можем определить и плоскость, определяемую ими.

Перейдите к следующей теореме.

На любой прямой m выберите точки A и B. Затем выберите две точки в пространстве C и D такие, что A, B, C и D не лежат в одной плоскости. Тогда у нас есть плоскости ABC и ABCD, которые пересекаются на прямой AB:

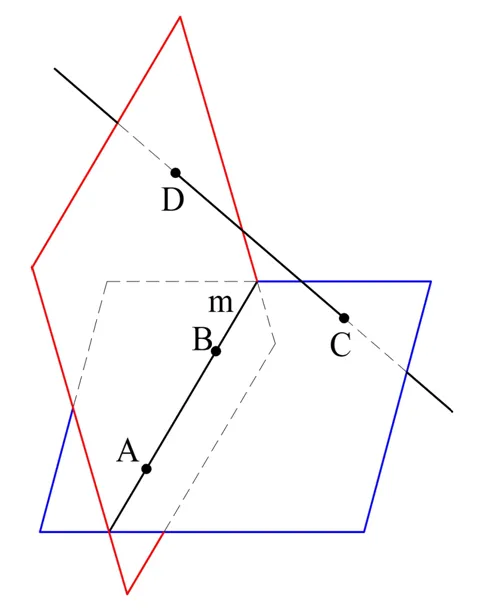
Теперь соедините C и D прямой линией. Линия CD состоит из бесконечного числа точек. Каждая из них может быть пересечена только плоскостью, проходящей через AB. Поскольку существует бесконечное число точек, существует также бесконечное число плоскостей. Остается показать, что никакие две из этих плоскостей не совпадают, т.е. все они различны.

Предположим, что две такие плоскости совпадают, т.е. фактически являются одной плоскостью. Затем доказывается, что эта плоскость проходит через две точки прямой CD. Согласно постулату 4, прямая CD тогда принадлежит этой плоскости, включая точки C и D. Но самолет также проходит через точки A и B. Таким образом, A, B, C и D являются частями одной плоскости, что не соответствует действительности. Это противоречие означает, что на самом деле все плоскости, проходящие через разные точки на прямой CD, различны, и так далее.

Рассмотрим еще одну теорему:

Предположим, что прямые m и n пересекаются. Обозначим точку их пересечения через A. Также для m выберем точку B, а для n — точку C. Подумав об этом, примите во внимание следующее. Мы можем построить плоскость a через A, B и C, и она будет единственной. Поскольку и A, и B принадлежат α, линия m также принадлежит α (Аксиома 4). Аналогично, прямая n лежит в плоскости α. Следовательно, α — это плоскость, упомянутая в теореме. Никакая другая плоскость не содержит прямые m и n, иначе она проходила бы через A, B и C, т.е. совместима с α.

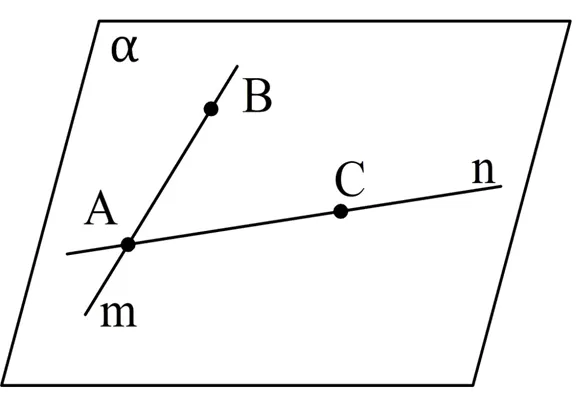
Эта теорема также утверждает, что две пересекающиеся прямые однозначно определяют плоскость, проходящую через них.

Плоскость, проходящая через данную прямую и точку

Теорема: Только плоскость может быть определена пересечением прямой с точкой, не лежащей на ней.

Доказательство.

Пусть AB — заданная прямая, а E — точка, не лежащая на ней. (Рис. 3) Проведите линию через AB и E. Тогда AB и AE пересекаются в точке A. Согласно аксиоме: существует только одна плоскость, проходящая через две пересекающиеся прямые, плоскость a, проходящая через эти прямые, единственна. Поскольку E принадлежит прямой AE, она лежит в плоскости α.

Предположим, что существует другая плоскость a’, проходящая через прямую AB и точку E, тогда эта плоскость пересекает плоскость a с прямой, содержащей A, B и E, согласно аксиоме 2. Это противоречит условию, так как точки A, B и E не лежат на одной прямой. Следовательно, плоскость a уникальна.

Рис. 3 Плоскость, проходящая через заданную прямую и точку.

Пересечение прямой с плоскостью

Теорема: Если две точки на прямой принадлежат плоскости, то вся прямая принадлежит данной плоскости.

Доказательство.

Пусть α — заданная прямая, A и B принадлежат этой прямой, α — заданная плоскость. A и B лежат в плоскости a. Согласно постулату 1, существует точка C, которая не лежит на прямой a. (рис. 4)

Постройте плоскость b, проходящую через прямую a и точку C. Поэтому если a и b конгруэнтны, то a принадлежит a, как гласит теорема. Если плоскости α и β не конгруэнтны, то они пересекаются прямой α’. Таким образом, мы имеем:

Точки A и B ∈ α, прямая a ∈ β, следовательно, точки A и B ∈β.

Из этого следует, что две точки A и B принадлежат двум плоскостям: a и b. Согласно аксиоме, они могут принадлежать только прямой a’, которая является пересечением этих плоскостей. Так как через две точки может проходить только одна прямая, и эта прямая по теореме равна α, то она является линией пересечения двух плоскостей. Поэтому α и α’ совпадают. Следовательно, α принадлежит плоскости α.

Теорема гласит, что плоскость и не плоскость не пересекаются в точке.

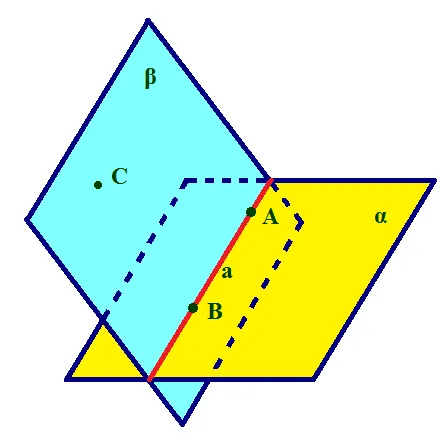
Рис. 4 Пересечение прямой с плоскостью.

Существование плоскости, проходящей через три данные точки

Теорема. Только плоскость может быть пересечена тремя точками, которые не принадлежат данной прямой. Рис. 5.

Доказательство. Предположим, что A, B и C не находятся на одной линии. Проведите прямые через точки A,C и B,C. Тогда они пересекаются в точке C. Согласно аксиоме: две пересекающиеся прямые могут быть пересечены одной плоскостью, плоскость, пересекаемая этими прямыми, единственна. Согласно теореме о пересечении прямых с плоскостью, обе прямые полностью принадлежат этой плоскости.

Рисунок 5 Существование плоскости, проходящей через три точки данных.

Репетитор: Васильев Алексей Александрович

Субъекты: Математика, физика, информатика, экономика, программирование.

Тел. 8 916 461-50-69, e-mail: [email protected]

6.Пример 1

Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Доказательство:

Даны прямая a и точка O, не принадлежащая прямой a. Даны прямые b, c, d, пересекающие их в точках B, C, D, которые пересекаются в точке O. Начертите плоскость a, проходящую через прямые a и O (рис. 6).

Согласно теореме о пересечении прямой с плоскостью, прямая b, проходящая через O и B, принадлежит плоскости a, так как две точки прямой b принадлежат плоскости a.

Если предположить, что прямая b не принадлежит плоскости a, то в этом случае можно построить плоскость a’, проходящую через точки B и O. Тогда a и a’ пересекаются прямой b’, проходящей через точки B и O. А поскольку из двух точек можно провести только одну прямую, b и b’ совпадают. Таким образом, b является целой линией плоскости a.

Аналогично доказываем, что прямые c и d принадлежат плоскости a. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, принадлежат одной плоскости.

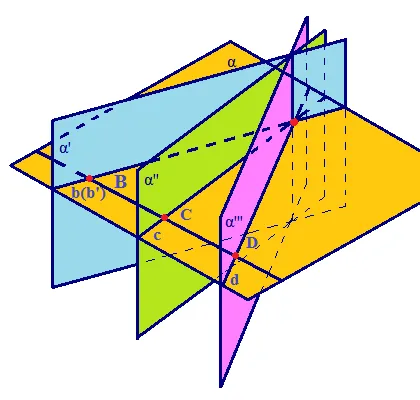
Рис. 6 Проблема. Докажите, что все прямые пересекают заданную прямую.

Пример 2

Даны две плоскости, которые не пересекаются. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает другую.

Доказательство:

Даны две непересекающиеся плоскости a и a’. И предположим, что прямая α пересекает плоскость a в точке B (рис. 7). Докажите, что α пересекает плоскость α’ в точке B’.

Возьмем точку A в плоскости a’ и проведем через нее и прямую a плоскость b. Тогда b пересекает плоскости a и a’ с параллельными прямыми b и b’. Точка B принадлежит прямой b, так как она принадлежит плоскости a и лежит на прямой a. Поэтому она принадлежит обеим плоскостям a и b.

Отсюда следует, что в плоскости β существуют две параллельные прямые β и β’. Одна из них пересекает α в точке B. Поэтому прямая a также пересекает вторую прямую b’. Поскольку, согласно аксиоме, существует только одна прямая b′, параллельная прямой b. Согласно аксиоме, можно пройти через точку B, которая не лежит на прямой b′. Отсюда следует, что прямая a не параллельна прямой b′, а пересекает ее в точке b′.

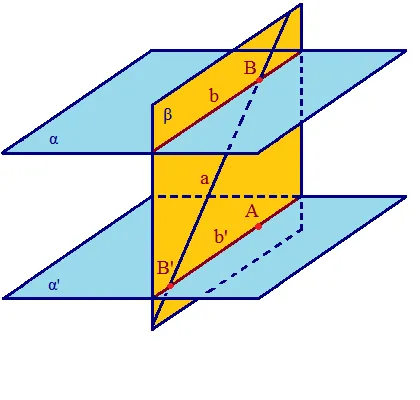
Аксиомы стереометрии

Все аксиомы планиметрии действительны и в стереометрии, а именно:

все точки или принадлежат данной прямой, или не принадлежат ей;
через любые 3500$-е точки можно провести 400$-ну прямую;
только одна из $3$-х точек на прямой может лежать между 3500$-мя другими;
длина любого отрезка прямой отлична от нуля;
длина отрезка складывается из длин частей, на которые он делится любой его точкой;
любой угол имеет определенную меру, отличную от нуля;
мера угла складывается из мер углов, на которые он делится любым лучем, проходящим между его сторонами;
аксиома Эвклида — через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Дополнительные аксиомы стереометрии

Скачайте учебную работу и получите отформатированную версию всего за 30 секунд 👍.

Все точки либо принадлежат заданной плоскости, либо не принадлежат ей. На диаграмме точки $A$ и $B$ принадлежат $\alpha$-плоскости ($\alpha$-плоскость проходит через эти точки), а точки $C$ и $D$ — нет.

Все точки прямой принадлежат плоскости, если все точки плоскости $3500$ принадлежат ей. На рисунке точки $A$ и $B$ прямой $s$ принадлежат плоскости $\alpha$, поэтому прямая $s$, которой принадлежат эти точки, также принадлежит плоскости $\alpha$.

На следующих рисунках показаны два случая, когда линия $s$ не лежит в плоскости.

Две плоскости пересекаются прямой, проходящей через общую точку этих плоскостей.

Студенческие работы, дипломные работы и другие работы, написанные студентами.
80% студентов, обратившихся за помощью, улучшили свои оценки.
Есть ли у вас трудности с письмом? Мы можем помочь! Получите список рекомендаций, уточните ошибки.

На диаграмме уровни $\alpha$ и $\beta$ имеют общую точку R, поэтому R принадлежит и $\alpha$, и $\beta$. R также принадлежит прямой $s$. Поэтому уровни $\alpha$ и $\beta$ пересекаются на линии $s$.

Один уровень может быть проведен через любые три точки, не лежащие на одной прямой. Другими словами, любые три точки в пространстве всегда лежат в одной плоскости.

На рисунке точки M, N и K не лежат на прямой $400$. Таким образом, существует единственная плоскость $\alpha$, которой принадлежат все эти точки.

Следствия из аксиом стереометрии.

Используя прямую $s$ и точку T, которая не лежит на ней, можно построить плоскость $400$-ne $\alpha$.

Используя 3500$ пересекающихся прямых p и q, можно построить плоскость $400$-на $\alpha$.

Плоскость может быть задана: a) $3$-пятью точками, не лежащими на прямой $400, b) прямой и точкой, не лежащей на ней, c) $3500-пятью пересекающимися прямыми, d) $3500-пятью параллельными прямыми.

Существует три возможных случая взаимного расположения линий в пространстве:

Стереометрия

Стереометрия (от греч. stereos, «solid» — «твердый, объемный, пространственный» и metreo, «metro» — «измерять») — это раздел геометрии, изучающий свойства фигур в пространстве. Основными (простейшими) формами в пространстве являются точки, линии и плоскости. В стереометрии существует новый тип взаимного расположения линий: пересекающиеся линии. Это одно из немногих существенных различий между стереометрией и планиметрией, поскольку во многих случаях проблемы стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Аксиомы стереометрии

На каждой прямой и в каждой плоскости имеются по крайней мере две точки.
В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник

Многогранник — это твердое тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников — ребрами и вершинами многогранника соответственно. Полиэдры могут быть выпуклыми и невыпуклыми. Выпуклый многогранник лежит на стороне плоскости, проходящей через одно из его ребер.

Литература

В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
И. Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Выпуск 31).

Математическая физика
Математическая химия
Математическая статистика
Математическое моделирование
Теория алгоритмов
Численные методы
Математическая экономика
Финансовая математика
Теория вероятностей
Исследование операций
Теория игр

Портал «Математика»
Категория «Математика»

Литератураправить | править код

В. В. Прасолов, И.Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
И.Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Вып.31).

Википедия Стереометрия адрес
Викисловарь — адрес
Викицитатник — адрес
Викиучебник — адрес
Викитека — адрес
Викиновости — адрес
Викиверситет — адрес
Викигид — адрес

Покажите и найдите стереометрию:

Вокруг света адрес
Академик адрес
Астронет адрес
Элементы адрес
Научная Россия адрес
Кругосвет адрес
Научная Сеть
Традиция — адрес
Циклопедия — адрес
Викизнание — адрес

Bing
Yahoo
Яндекс
Mail.ru
Рамблер
Нигма.РФ
Спутник
Google Scholar
Апорт
Архив Интернета
Научно-популярные фильмы на Яндексе
Документальные фильмы

Список ru-вики
Вики-сайты на русском языке
Список крупных русскоязычных википроектов
Каталог wiki-сайтов
Русскоязычные wiki-проекты
Викизнание:Каталог wiki-сайтов
Научно-популярные сайты в Интернете
Лучшие научные сайты на нашем портале
Лучшие научно-популярные сайты
Каталог научно-познавательных сайтов
НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов

Страница — краткая статья
Страница — энциклопедическая статья
Разное — на страницах :, , ,

Основные понятия стереометрии

Стереометрия — это раздел геометрии, изучающий свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «stereos» — объемный, пространственный и «metreo» — измерять.

Многогранник — это геометрическое тело, ограниченное конечным числом плоских многоугольников, два из которых, имея общую сторону, не лежат в одной плоскости. Сами многоугольники называются гранями, их стороны — ребрами многогранника, а их вершины — вершинами многогранника.

Форма, образованная всеми гранями многогранника, называется площадью поверхности (полной площадью поверхности), а сумма площадей всех граней — площадью (полной) поверхности.

Куб — это многогранник с шестью сторонами, которые являются квадратами одинакового размера. Стороны квадратов называются ребрами куба, а углы — вершинами куба.

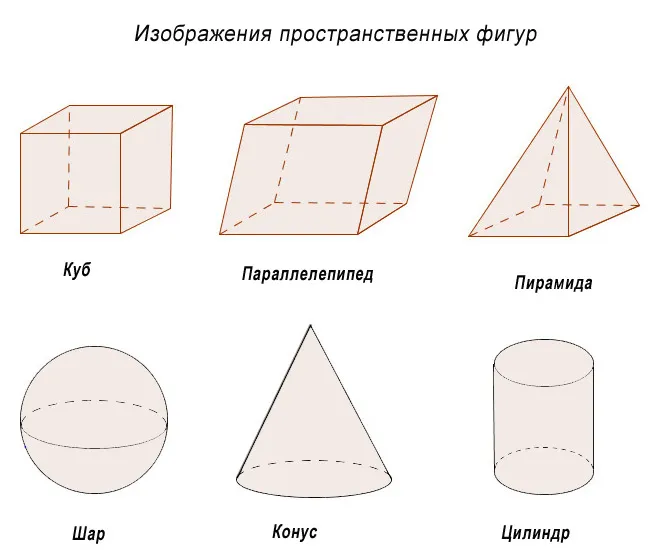
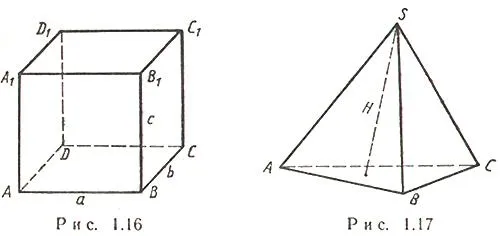
Параллелограмм — это многогранник с шестью гранями, каждая из которых является параллелограммом. Стороны параллелепипеда называются ребрами параллелепипеда, а их вершины — углами параллелепипеда. Две грани параллелепипеда называются противоположными, если они не имеют общего ребра, а те, которые имеют общее ребро, называются смежными. Иногда две противоположные грани параллелепипеда обозначаются и называются основаниями, в этом случае другие грани являются боковыми, а их стороны, соединяющие вершины оснований параллелепипеда, — его боковыми гранями.

Параллелепипед — это параллелепипед с прямоугольниками на гранях.

Параллелепипед — это параллелепипед, все стороны которого являются прямоугольниками. Обратите внимание, что каждый прямоугольный параллелограмм является прямоугольным параллелограммом, но не каждый прямоугольный параллелограмм является прямоугольным параллелограммом.

Первая аксиома стереометрии

Любые три точки, не лежащие на одной прямой, пересекаются плоскостью, и только одна из них.

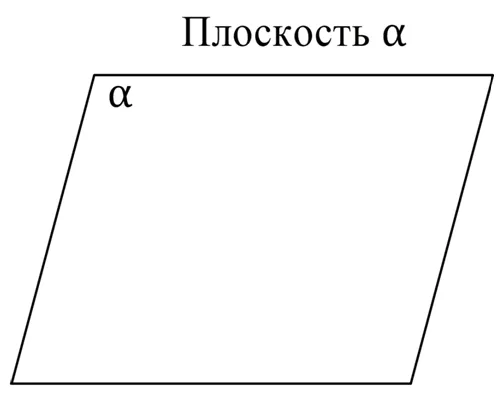
Плоскость — это беспредельная однородная поверхность.

Плоскость обозначается тремя буквами греческого алфавита: a (альфа), b (бета), c (гамма).

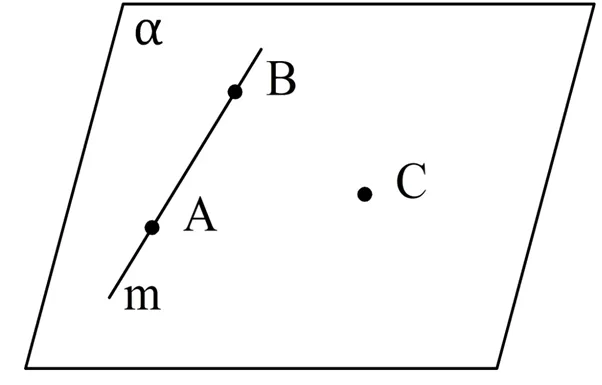
На рисунке 1 показана альфа-плоскость.

Вторая аксиома стереометрии

Если две точки на прямой лежат в плоскости, то все точки на прямой также лежат в этой плоскости.

Если мы посмотрим на рисунок 2 — точки A и B на прямой alpha лежат в плоскости b, то все точки на этой прямой лежат в плоскости b.

Третья аксиома стереометрии

Если две плоскости имеют общую точку, то у них есть общая прямая, по которой они пересекаются.

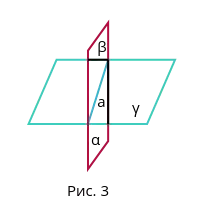
Плоскость c пересекает плоскость a (Рисунок 3).