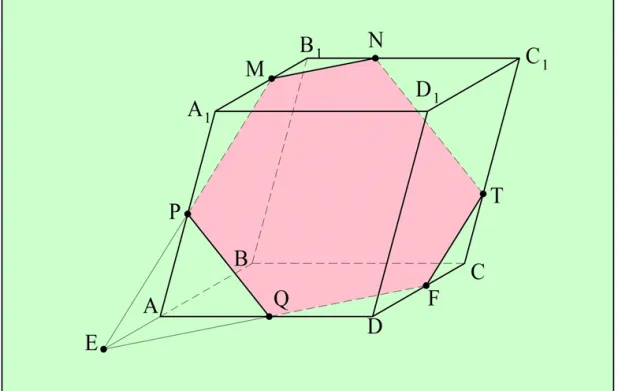
Задание. Отрезок AB не пересекает плоскость a, а отрезок C D принадлежит a. Известно, что отрезки AC и BD перпендикулярны a:
Перпендикулярные прямые
Когда две пересекающиеся линии образуют угол 90 градусов, эти линии называются перпендикулярными.
Схематично перпендикулярные линии AC и BD выглядят следующим образом:
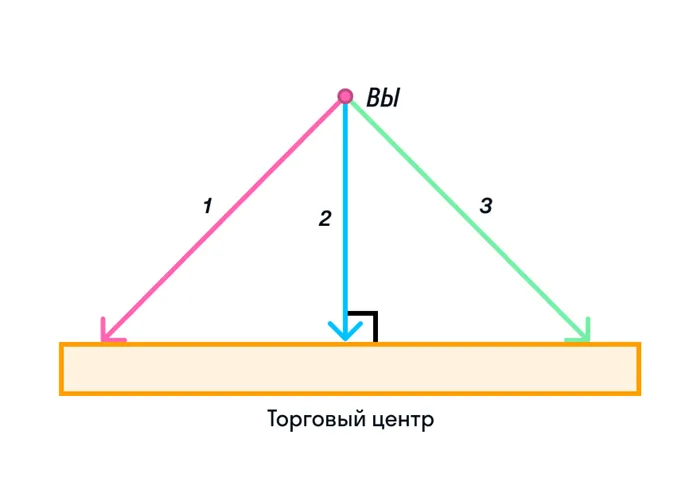
В геометрии перпендикулярные линии обозначаются следующим образом:
Внимание! Если учитель обнаружит плагиат в вашей работе, у вас будут серьезные неприятности (вплоть до исключения из школы). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Признак перпендикулярности, какие условия необходимы, чему равен угол
Угол между парой пересекающихся линий в пространстве может быть прямой линией. В данном случае рассматриваемые линии перпендикулярны друг другу.
Если угол между двумя пересекающимися прямыми равен прямому углу, то эти прямые также перпендикулярны друг другу. Из этого утверждения можно сделать вывод, что перпендикулярные линии могут пересекаться на плоскости, а перпендикулярные линии могут пересекаться и скрещиваться в пространстве. Таким образом, выражения «линии a и b перпендикулярны» и «линии b и a перпендикулярны» можно считать одинаковыми. После этого определения мы вводим понятие взаимно перпендикулярных прямых.
При определении перпендикулярности линий необходимо учитывать их характеристики, которые имеют большое значение при решении задач. Основные характеристики:
- Через какую-то точку А возможно начертить единственную перпендикулярную линию основному отрезку, остальные линии будут являться наклонными и могут скрещиваться.
- Несколько перпендикуляров ни при каких условиях не будут между собой пересекаться.
Например, мы можем нарисовать линию PQ и пару перпендикулярных к ней линий: AA и BB. Докажите, что эти линии не имеют пересечений.
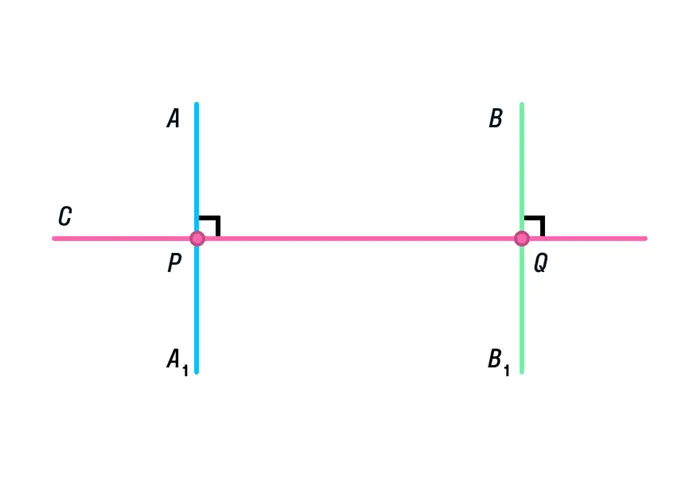
Это полезно доказывать с помощью обратного метода. Предполагая, что прямые пересекаются в точке M1, найдите точку M в другой полуплоскости относительно прямой PQ. Таким образом, две точки пересекают две прямые, что не согласуется с аксиомой. Следовательно, гипотеза ложна и линии AA и BB не имеют пересечений:
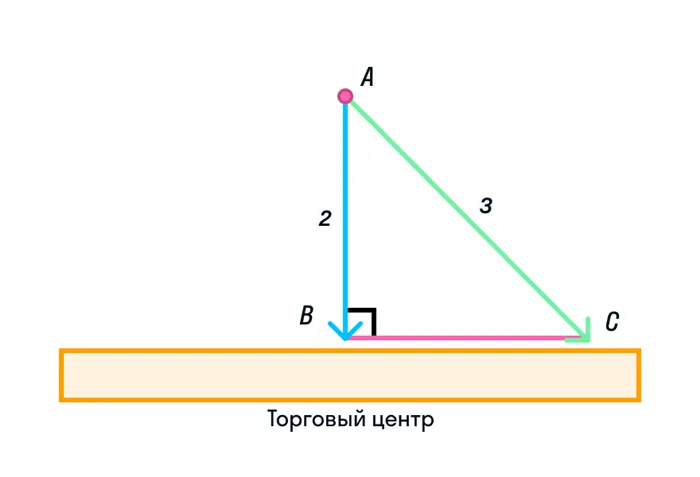
Можно сделать вывод, что две прямые, перпендикулярные третьей прямой, не имеют общих точек пересечения.
Теорема о перпендикулярных прямых, как доказать
Задачи с перпендикулярными линиями обычно решаются путем рассмотрения свойств этих линий. Доказательством перпендикулярности линий является прямой угол, который они образуют. Если необходимо определить перпендикулярность линий на основе известных уравнений ортогональной системы координат, то следует применить необходимое и достаточное условие перпендикулярности линий.
Теорема 1
Для того чтобы прямые a и b были перпендикулярны друг другу, необходимо и достаточно, чтобы ведущий вектор a прямой был перпендикулярен ведущему вектору b данной прямой.
Доказательством этой теоремы является определение ведущего вектора прямой линии и перпендикуляра к прямым линиям.
Предположим, у нас есть ортогональная декартова система координат Оху с уравнениями для линии на плоскости, определяющими прямые a и b. Уравнения для линии на плоскости следующие. Векторы направлений заданных линий a и b можно обозначить следующим образом:
Согласно формуле для прямых a и b необходимым и достаточным условием является то, что векторы \(\vec\) и \(\vec.\) перпендикулярны друг другу.
Это имеет место в случае скалярного произведения векторов:
Таким образом, необходимым и достаточным условием перпендикулярности прямых a и b, лежащих в плоскости в ортогональной системе координат Оху, является следующее выражение:
Эта теорема подходит, если нужно определить координаты ведущих векторов или если известны нормальные или параметрические уравнения линий в плоскости заданных прямых a и b.
Необходимое и достаточное условие перпендикулярности прямых a и b можно перенести в трехмерное пространство.
В этом случае обозначения будут следующими:
являются ведущими векторами прямых a и b.
Теорема 2
Линии a и b на плоскости перпендикулярны друг другу, если нормальный вектор линии a и вектор линии b перпендикулярны друг другу. Это условие считается необходимым и достаточным.
Доказательство теоремы состоит в применении рассмотренного условия, когда уравнения прямых позволяют быстро определить координаты нормальных векторов заданных прямых. Дано общее уравнение прямой линии вида: \( A_+B_+C=0\)
а также уравнение прямой линии в отрезках вида:
и уравнение прямой линии с угловым коэффициентом вида y = kx + b, можно определить координаты векторов.
В случае, когда линия a в плоскости определяется уравнением с угловым коэффициентом:
и строка b имеет вид:
тогда координаты нормальных векторов будут следующими:
Условие перпендикулярности соответствует выражению:
Теорема 3
Линии a и b перпендикулярны плоскости при необходимом и достаточном условии, что один из направляющих векторов этих линий совпадает с вектором нормали второй линии.
Это условие выполняется, если можно определить вектор одной прямой и координаты вектора нормали другой прямой. Одна линия должна быть представлена нормальным или параметрическим уравнением, а другая линия — общим уравнением прямой, уравнением пересечения или уравнением с угловым коэффициентом.
Насколько полезной для вас была эта статья?
Основные определения
Перпендикулярные линии — это линии, которые пересекаются под углом 90 градусов. Перпендикулярные линии обозначаются так: a ┴ b .
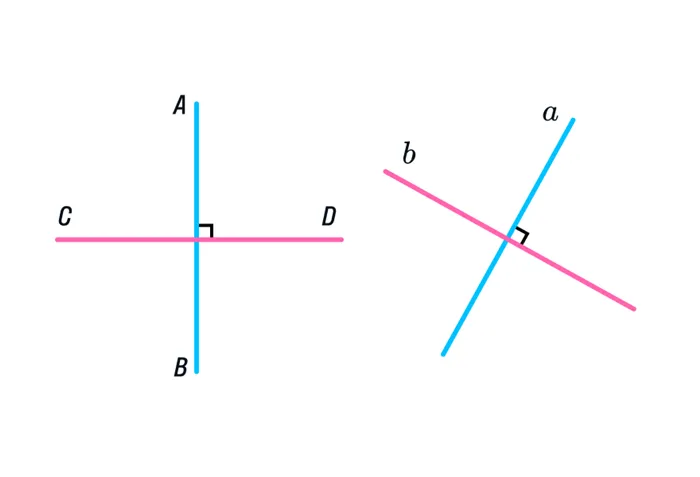
Угол в 90 градусов в математике называется прямым углом и называется квадратом.
Еще один интересный факт из мира геометрии: если угол при пересечении двух прямых равен 90°, то все остальные углы являются прямыми, а их сумма равна 360°.
Прямоугольные отрезки — это отрезки, лежащие на прямых.
Отрезки не обязательно должны пересекаться, чтобы называться прямоугольными. Достаточно, если угол между прямыми, на которых они лежат, равен 90°.
В качестве задачи на звездочку давайте вспомним, в каких фигурах могут встречаться вертикальные отрезки (стороны)? Вероятно, вы сразу подумали о квадрате и прямоугольнике, но прямоугольный треугольник и даже прямоугольная трапеция также подходят — вы узнаете об этом на уроках геометрии в 8 классе.
Различные элементы внутри фигуры также могут быть расположены перпендикулярно странице. Попробуйте отложить диаметр и радиус круга, две хорды, биссектрису треугольника перпендикулярно друг другу (кстати, последнее задание работает, только если вы проводите биссектрису угла при основании равнобедренного треугольника).
Как мы видим, прямые линии часто пересекаются под углом 90 градусов. Можно сказать, что это своего рода нормальное, повседневное поведение прямых линий. Прямые углы окружают нас повсюду: в помещении, на оживленных улицах, в бассейне, даже в нашей любимой книге.
Выясните, в каких предметах вы «хромаете», а затем работайте над ними без формул и скучных лекций.

Способы построения перпендикулярных прямых
Но как можно построить вертикальные линии? Что вам для этого нужно? Давайте рассмотрим все доступные нам методы.
Самое простое — использовать транспортир. Постройте прямую a и точку A, которая не лежит на этой прямой. Совместите значение 90 градусов с точкой так, чтобы нижняя часть транспортира как линейки полностью совпадала с линией, и сделайте надрез в отверстии транспортира. Соедините точку А с конным шерифом до пересечения с прямой линией.
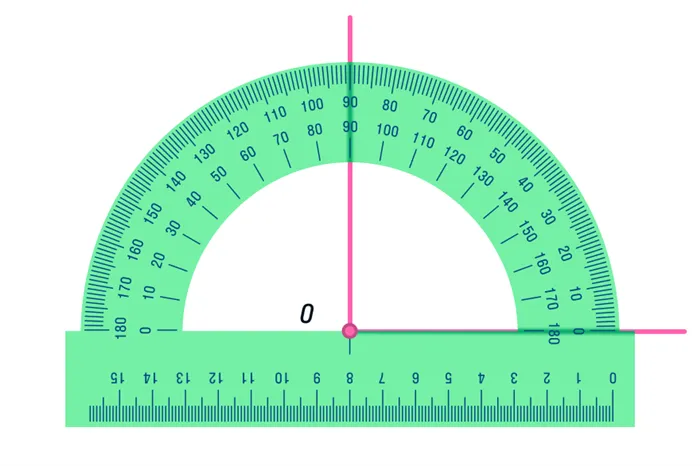
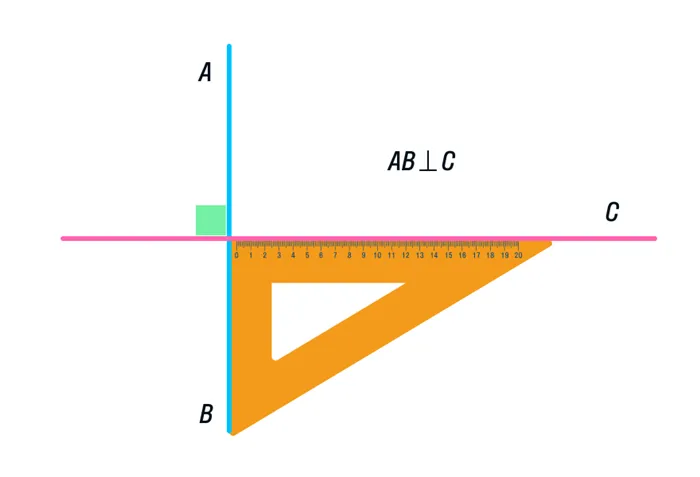
Но что делать, если транспортир забыт дома, а в наличии только линейка и транспортир? Внимательно рассмотрите рисунок и потренируйтесь рисовать дома.
Теорема о перпендикулярных прямых и ее доказательство
Линия, перпендикулярная прямой, может проходить через любую точку прямой и только через одну из них.
«Кто это вообще придумал?» Вы можете возразить. «Почему мы должны в это верить? Что, если все обстоит иначе и нас обманывают?». Если да, то ваши возражения — признак любознательного ума!
Что такое теорема? Это утверждение, которое требует доказательств. Это значит, что никто не принимает это как должное: ни вы, ни учитель, ни величайший ученый. Существует множество способов доказательства теорем, одним из которых является отрицательный метод. Использовать этот термин — все равно что согласиться с противоположным утверждением, а затем подумать о том, что из него следует.
Например, попробуем доказать утверждение «Осенью черные дрозды улетают на юг», используя противоположный метод. Предположим, что черные дрозды зимуют в наших городах. Тогда осенью и зимой мы должны видеть их повсюду, и в небе не должно быть никаких признаков массовой миграции. Действительно ли это так? Конечно, нет.
Теперь попробуем доказать теорему о вертикальных линиях этим методом.
Предположим, что теорема ложна, а значит, через точку на прямой можно провести множество перпендикулярных прямых.
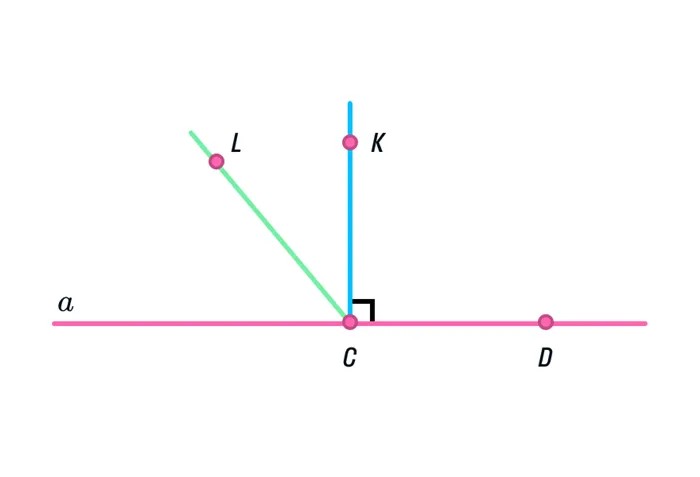
- Возьмем линейку и проведем прямую а, отметив на ней точки С и D .
- Далее построим перпендикулярную прямую из точки С. Угол КСD равен 90°.
- Отрезок КС находится на прямой, перпендикулярной а .
- Предположим, что есть еще одна прямая, перпендикулярная а. Проведем ее через точку С и отметим на ней точку L .
- Тогда угол LCD равен 90° и угол КСD равен 90°.
- Пункт номер 5 невозможен: от отрезка CD можно отложить только один прямой угол в данной плоскости.
- А значит, через точку С можно провести только одну прямую, перпендикулярную прямой а .
Как доказать: ты хороший!
Уделяйте этому 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.