В пикритических выкладках мы увидим с множителями числа, из которых можно извлечь квадратный корень. Вычтите квадратные корни из ступеней и подставьте числа в качестве коэффициентов квадратных корней.
Пример 2
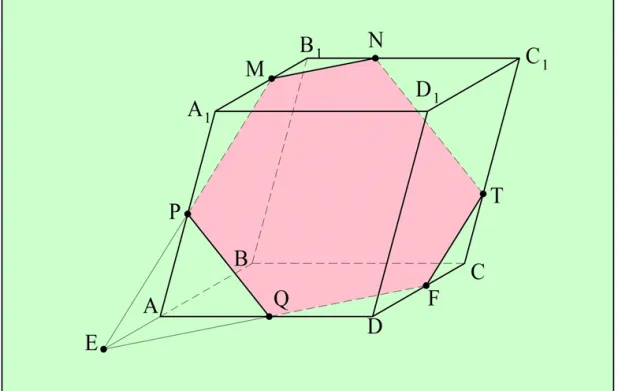
Возьмите квадратный корень из 0,16:
Представим десятичное значение в виде обыкновенной дроби:
Теперь мы хотим использовать свойство корней:
Извлеките корни из числителя и знаменателя с помощью квадратной матрицы:
Узнайте больше в этой статье:
- что такое «извлечение корня»;
- в каких случаях он извлекается;
- принципы нахождения значения корня;
- основные способы извлечения корня из натуральных и дробных чисел.
Что такое «извлечение корня»
Сначала введем определение извлечения корня.
Извлечение корня — это поиск ценности корня.
Если из a извлечь корень со степенью n, то найдется число b, степень n которого равна a. Если вы найдете такое число b, то можно сказать, что корень извлечен.
Выражения «извлечение корня» и «нахождение значения корня» эквивалентны.
В каких случаях извлекается корень?
Корень с n степенью можно извлечь из a ровно тогда, когда a можно представить как n степень числа b.
4 = 2 × 2, поэтому из числа 4 можно извлечь квадратный корень, равный 2.
Если корень n-й степени из числа a не может быть представлен в виде корня n-й степени из числа b, то этот корень не извлекается или из него можно извлечь только приближенное значение корня с точностью до десятичного знака.
Квадратный корень из произведения и дроби

На этом уроке мы рассмотрим основные свойства квадратных корней (наборы квадратных корней для произведения и дроби). Мы научимся применять их при преобразовании выражений, содержащих квадратные корни.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим учебным видео в комплекте, вам необходимо добавить его в свой личный шкафчик.


2. Распространите видеоуроки среди своих учеников в личных кабинетах.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Квадратный корень из произведения и дроби»
Во-первых, давайте вспомним определение арифметического квадратного корня. Таким образом, арифметический квадратный корень из a — это неотрицательное число, квадрат которого равен a.
Обратите внимание, что
Мы видим, что квадратный корень из произведения двух неотрицательных чисел равен произведению квадратных корней этих чисел.
Квадратный корень из произведения любых двух неотрицательных чисел обладает этим свойством.
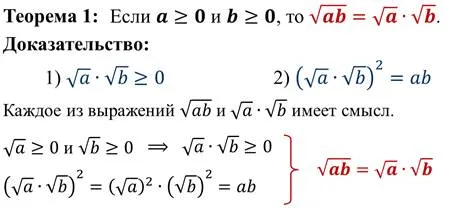
Чтобы извлечь квадратный корень из произведения неотрицательных чисел, его можно извлечь из каждого коэффициента отдельно и умножить результат на .
Обратите внимание, что это свойство также имеет место в случае, когдаподчинённыйВыражениеэто произведение трех, четырех и т.д.неотрицательныйМультипликаторы.

Произведение корней неотрицательных коэффициентов равно произведению корней этих коэффициентов.
Обратное также верно: произведение корней из неотрицательных чисел равно произведению этих чисел.
Упражнение: Вычислите значение выражения.
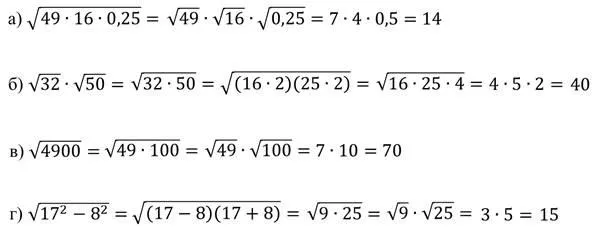
Теперь рассмотрим арифметический квадратный корень из дроби.

Мы видим, что квадратный корень из дроби равен квадратному корню из числителя, деленному на квадратный корень из знаменателя.
Это свойство квадратного корня из дроби, числитель которой равеннеотрицательное числои знаменательположительный.

Чтобы получить квадратный корень из дроби, можно взять корень из числителя и знаменателя отдельно и разделить первый результат на второй.
Вывод: Квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
И наоборот, корень из корней равен корню из квадрата этих чисел.
Выполните задание: Вычислите значение выражения.

Корень из неотрицательных кратных равен произведению корней из этих кратных.
Корень дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя.
Как извлечь корень из дроби
Калькулятор предназначен для решения следующих задачпервые дробии дробей с целыми числами (смешанныйВ будущем планируется ввести функцию для решения десятичных дробей, но пока она недоступна.
Для того чтобы работать с дробным калькулятором, необходимо понять очень простой принцип ввода данных. Все целые числа вводятся с помощью больших клавиш слева. Все числители вводятся с помощью маленьких белых кнопок в правом верхнем углу поля чисел. Все знаменатели вводятся нажатием кнопок в правом нижнем углу соответственно. Такой способ ввода данных является в некотором смысле инновационным, поскольку он четко разделяет целое число, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным.
Предположим, вы хотите возвести в шестую степень квадратный корень из двух пятых и двух девяток. Начните импортировать пример, нажав на кнопку квадратного корня. Затем нажмите на цифру 2 в области числителя и на цифру пять в области знаменателя. Первая сумма готова. Теперь нажмите символ «+» — это действие добавления. Затем введите на основной клавиатуре целое число, затем число два в области числителя и девять в области знаменателя. Затем нажмите клавишу степени «^», за которой следует цифра шесть на основной клавиатуре. В результате будет получен окончательный пример:
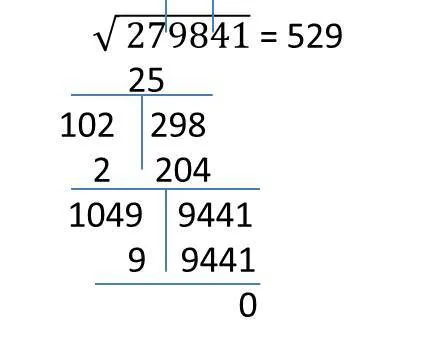
Теперь нажмите клавишу «равно», и вы получитерезультат расчета.. Приведенный выше пример иллюстрирует практически весь арсенал возможностей дробного калькулятора. Таким же образом можно умножать, делить или вычитать простые или алгебраические дроби, дроби с одинаковыми или разными знаменателями, дроби с целыми числами и т.д., а также калькулятор может вычислять дроби в процентах, что не часто требуется, но, тем не менее, необходимо для решения многих текущих задач.
Если вы хотите преобразовать положительное число в отрицательное, сначала введите число, а затем нажмите клавишу «+/-«. Число или дробь автоматически заключаются в отрицательные скобки или наоборот (в зависимости от начального состояния числа). Если вы хотите удалить число, числитель или знаменатель, используйте соответствующую стрелку назад, расположенную в полях числителя и знаменателя. Стрелки работают аналогичным образом и поочередно удаляют цифры или символы на экране калькулятора.
Управление калькулятором дробей с клавиатуры.
Онлайн-калькулятором дробей можно управлять не только с помощью компьютерной мыши, но и с помощью клавиатуры. Логика здесь очень проста:
- Все целые числа вводятся как обычно, нажатиями на клавиши чисел.
- Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1).
- Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).
Операции умножения, деления, сложения и вычитания также вызываются соответствующими клавишами на клавиатуре, если таковые имеются (обычно с правой стороны, в так называемой области numpad). Удаление выполняется нажатием клавиши backspace. Действие удаления (красная клавиша «C») вызывается нажатием клавиши «C». Квадратный корень активируется нажатием соседней клавиши «V». Удаление производится нажатием клавиши backspace.
Зачем нужен калькулятор дробей онлайн?

Онлайн-калькулятор дробей был разработан для решения следующих задачобычныйисмешанныйДроби (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и студентам университетов. Наш калькулятор предлагает возможность работать с дробями путем деления, умножения, сложения и вычитания дробей. Калькулятор также может обрабатывать корни и силы и даже может работать с отрицательными числами, что делает его вдвойне лучше дробей.лучше, чемПохожие онлайн-приложения.
Онлайн-калькулятор дробей поможет вам решить примеры с дробями, и вам не придется беспокоиться о неправильных дробях. Это делаетсяавтоматическиПриложение автоматически вычисляет общий знаменатель и выводит результат на экран.
В чем преимущества такого способа решения дробей?
Калькулятор поддерживает операции со скобками, позволяя решать дроби даже для сложных математических примеров. В частности, операции со скобками часто требуются при вычисленииалгебраические дробиήотрицательные дробиДроби, с которыми регулярно приходится иметь дело всем учащимся средней школы. Вы также можете использовать этот калькулятор длясокращать дробьили решать дробис разными знаменателями.. Также, в отличие от многих других бесплатных сервисов, этот калькулятор может работать с двумя, тремя, четырьмя или любым количеством дробей и чисел.
Калькулятор дробей полностью бесплатен и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Вы можете работать с помощью мыши или непосредственно с клавиатурой (это относится как к цифрам, так и к действиям). Мы постарались реализовать максимально удобный интерфейс для дробей, чтобы сложные математические расчеты стали для вас удовольствием! 🙂
Квадратные корни
Вторая таблица — это таблица квадратных корней:
| √x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 1,41421 | 1,73205 | 2 | 2,23607 | 2,44949 | 2,64575 | 2,82843 | 3 |
| 1 | 3,16228 | 3,31662 | 3,4641 | 3,60555 | 3,74166 | 3,87298 | 4 | 4,12311 | 4,24264 | 4,3589 |
| 2 | 4,47214 | 4,58258 | 4,69042 | 4,79583 | 4,89898 | 5 | 5,09902 | 5,19615 | 5,2915 | 5,38516 |
| 3 | 5,47723 | 5,56776 | 5,65685 | 5,74456 | 5,83095 | 5,91608 | 6 | 6,08276 | 6,16441 | 6,245 |
| 4 | 6,32456 | 6,40312 | 6,48074 | 6,55744 | 6,63325 | 6,7082 | 6,78233 | 6,85565 | 6,9282 | 7 |
| 5 | 7,07107 | 7,14143 | 7,2111 | 7,28011 | 7,34847 | 7,4162 | 7,48331 | 7,54983 | 7,61577 | 7,68115 |
| 6 | 7,74597 | 7,81025 | 7,87401 | 7,93725 | 8 | 8,06226 | 8,12404 | 8,18535 | 8,24621 | 8,30662 |
| 7 | 8,3666 | 8,42615 | 8,48528 | 8,544 | 8,60233 | 8,66025 | 8,7178 | 8,77496 | 8,83176 | 8,88819 |
| 8 | 8,94427 | 9 | 9,05539 | 9,11043 | 9,16515 | 9,21954 | 9,27362 | 9,32738 | 9,38083 | 9,43398 |
| 9 | 9,48683 | 9,53939 | 9,59166 | 9,64365 | 9,69536 | 9,74679 | 9,79796 | 9,84886 | 9,89949 | 9,94987 |
Числа в кубе
И третья, конечно же, таблица куба, которая используется для извлечения корня куба.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1331 | 1728 | 2197 | 2744 | 3375 | 4096 | 4913 | 5832 | 6859 |
| 2 | 8000 | 9261 | 10648 | 12167 | 13824 | 15625 | 17576 | 19683 | 21952 | 24389 |
| 3 | 27000 | 29791 | 32768 | 35937 | 39304 | 42875 | 46656 | 50653 | 54872 | 59319 |
| 4 | 64000 | 68921 | 74088 | 79507 | 85184 | 91125 | 97336 | 103823 | 110592 | 117649 |
| 5 | 125000 | 132651 | 140608 | 148877 | 157464 | 166375 | 175716 | 185193 | 195112 | 205379 |
| 6 | 216000 | 226981 | 238328 | 250047 | 262144 | 274625 | 287496 | 300763 | 314432 | 328509 |
| 7 | 343000 | 357911 | 373248 | 389017 | 405224 | 421875 | 438976 | 456533 | 474552 | 493039 |
| 8 | 512000 | 531441 | 551368 | 571787 | 592704 | 614125 | 636056 | 658503 | 681472 | 704969 |
| 9 | 729000 | 753571 | 778688 | 804357 | 830584 | 857375 | 884736 | 912673 | 941192 | 970299 |
Эти числа возводятся в третью степень.
Он называется «кубик», потому что используется для вычисления объема куба. Другими словами, нужно возвести длину ребра куба в третью степень.
Такие таблицы довольно просты в использовании. Слева — десятки, справа — единицы. С их помощью можно легко и быстро извлечь корень из числа от 0 до 99. Это был метод извлечения корня, который я считаю самым простым после инструмента вычисления — калькулятора, но, как уже говорилось, мы не всегда можем им воспользоваться. Поэтому давайте перейдем к другим интересным и на первый взгляд сложным решениям.
Разложение подкоренного числа на простые множители
Перейдем от более удобного и быстрого метода к более сложному и рассмотрим второй из них — разложение числа корня на простые множители.
Этот метод заключается в представлении числа в виде степени с необходимой экспонентой, из которой можно вывести значение корня.
Пример 1:
Возьмите число 196. Чтобы найти квадратный корень, разделите число на простые множители: √196=2×2×2×7×7×7×7=2²×7²
Теперь действуйте следующим образом: 2×7=14.
Объяснение:
Кратные числа находятся следующим образом: Разделите 196 на 2 и получите число 98, которое также делится на 2. Продолжайте делить до тех пор, пока деление не станет невозможным. Например, число 49 нельзя разделить пополам, поэтому мы используем метод соответствия. Мы находим число, которое является делимым. В данном случае это 7. Два числа, которые мы имеем (2 и 7), перемножаются вместе, но без силы, что дает 14, которое является квадратным корнем из 196.
Пример 2:
Чтобы лучше понять, как мы делим на кратное, возьмем другое число и посмотрим на силу. Разделить 441 на 2 невозможно, поэтому получаем число. Оно делится дважды на 3. Снова получаем 49, которые дважды делим на 7. Следовательно, √441 = 3×3×3×7×7 = 3²×7².
3×7=21. Следовательно, ответ √441=21.
Объяснение:
Мы умножили 3 на 7, потому что это два числа степени 2. Если бы одно из них имело степень 4, например: 3⁴×7², — пришлось бы сделать: 3×3×7. Проще сказать, что мы уменьшаем степени ⁴ и ².
Вторичные числа, которые разлагаются на простые коэффициенты, могут иметь только четные степени.
Финальные вычисления
Таким образом, у нас остается два номера в качестве кандидатов. Как узнать, какой из них является корнем? Ответ очевиден: квадрат двух чисел. Корень — это тот, который возводит в квадрат исходное число.
Например, мы нашли два кандидата на число 3364: 52 и 58. Мы должны возвести их в квадрат:
52 2 = (50 +2) 2 = 2500 + 2 — 50 — 2 + 4 = 2704; 58 2 = (60 — 2) 2 = 3600 — 2 — 60 — 2 + 4 = 3364.
Вот и все! Результат — 58! Для упрощения расчетов я использовал формулу для суммы и квадрата разности. Таким образом, мне даже не пришлось перемножать числа в колонках! Это еще один уровень оптимизации вычислений, но, конечно, совсем не обязательный 🙂 .
Примеры вычисления корней
Теория — это, безусловно, хорошо. Но давайте проверим это на практике.
Задача. Вычислите квадратный корень:
Сначала давайте выясним, между какими цифрами находится число 576:
Теперь давайте посмотрим на последнюю цифру. Она равна 6. Когда это бывает? Только если корень заканчивается на 4 или 6. Возьмем два числа:
Остается только возвести каждое число в квадрат и сравнить его с исходным числом:
24 2 = (20 + 4) 2 = 576
Идеально! Первый квадрат соответствует исходному числу. Это означает, что это корень.
Задача. Вычислите квадратный корень:
Здесь и далее я опишу только основные шаги. Поэтому мы ограничиваем их количество:
Мы смотрим на последнюю цифру:
Давайте разберемся с этим:
33 2 = (30 + 3) 2 = 900 + 2 — 30 — 3 + 9 = 1089 ≠ 1369; 37 2 = (40 — 3) 2 = 1600 — 2 — 40 — 3 + 9 = 1369.
Задача. Вычислите квадратный корень:
Мы смотрим на последнюю цифру:
Давайте разберемся с этим:
52 2 = (50 + 2) 2 = 2500 + 2 — 50 — 2 + 4 = 2704;
Ответ — 52. Возводить второе число в квадрат не нужно.
Задача. Вычислите квадратный корень:
Мы смотрим на последнюю цифру:
Как показано на рисунке, после второго шага остается только один вариант: 65. Это квадратный корень. Но давайте взвесим и проверим:
65 2 = (60 + 5) 2 = 3600 + 2 — 60 — 5 + 25 = 4225;
Правильно. Запишите ответ.
Студенты всегда спрашивают: «Почему я не могу использовать калькулятор на экзамене по математике?». Как найти квадратный корень из числа без калькулятора?». Давайте попробуем ответить на этот вопрос.
Как же извлечь квадратный корень из числа без использования калькулятора?
Энергия получения квадратного корня обратна энергии возведения в квадрат.
Если взять квадратный корень из положительного числа и возвести результат в квадрат, то получится то же самое число.
Небольшие числа, которые являются точными квадратами натуральных чисел, например, 1, 4, 9, 16, 25, …,100, можно устно вывести из квадратных корней. Обычно в школе изучают таблицу квадратов натуральных чисел до двадцати. Знать квадратные корни из чисел 121, 144, 169, 196, 225, 256, 289, 324, 361, 400. Корни можно извлекать из чисел больше 400 методом подгонки с несколькими подсказками. Попробуем рассмотреть пример этого метода.
Пример: извлечение корня из числа 676 .
Примечание: 20 2 = 400 и 30 2 = 900, поэтому 20 2 = 400 и 30 2 = 900, поэтому 20 2 = 900.<√676<900.
Точные квадраты целых положительных чисел оканчиваются на 0, 1, 4, 5, 6, 9. Число 6 дает 4 2 и 6 2. Поэтому, когда извлекается корень из 676, он равен либо 24, либо 26.
Остается проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26.
Другой пример: √6889 .
Поскольку 80 2 = 6400 и 90 2 = 8100, то 80 2 = 6400 и 90 2 = 8100, 80 2 = 6800.<√6889<90. Цифру 9 дают 3 2 и 7 2, то √6889 равен либо 83, либо 87.
Тест: 83 2 = 6889.
Ответ: √6889 = 83 .
Если вам трудно решить задачу методом подбора, вы можете разделить частичное выражение на коэффициенты.
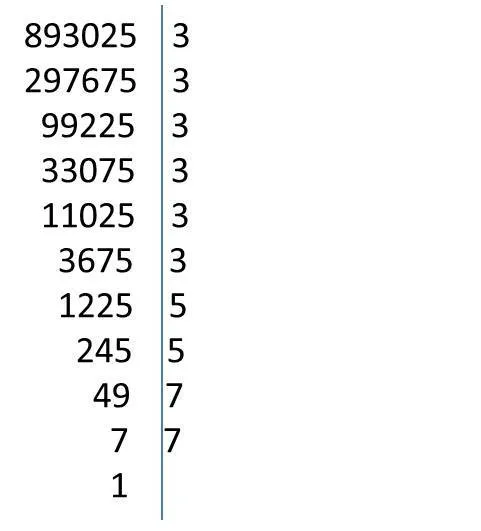
Например, найдите √893025 .
Разложите 893025 на кратные числа, помня, что вы делали это в шестом классе.
Корень из числа: правила вычисления и примеры
Итак, мы возвели число 2 в квадрат, то есть умножили его на себя, и получили 4. Но как получить квадратный корень из 4? Сразу скажем, что корни могут быть квадратными, кубическими или любой степени до бесконечности.
Степень корня всегда является натуральным числом, а это значит, что нельзя решить такое уравнение: корень степени 3,6 из n.
Квадратный корень
Вернемся к вопросу о том, как извлечь квадратный корень из 4. Поскольку мы возвели в квадрат число 2, мы также извлечем квадратный корень. Чтобы правильно вывести квадратный корень из 4, нам просто нужно найти число, которое при возведении в квадрат дает нам число 4. И это, конечно же, 2. Посмотрите на этот пример:
Этот пример довольно прост. Давайте попробуем извлечь квадратный корень из 64. Какое число, умноженное само на себя, дает 64? Очевидно, что это 8.
Кубический корень
Как уже упоминалось, возможны не только квадратные корни. Давайте на примере более подробно объясним, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня такой же, как и квадратного, с той лишь разницей, что число, о котором идет речь, сначала умножается на себя не один, а два раза. То есть, давайте рассмотрим следующий пример:
- 3x3x3=27
- Естественно, кубическим корнем из числа 27 будет тройка:
- Корень 3 из 27 = 3
Предположим, нам нужно найти кубический корень из 64. Чтобы решить это уравнение, достаточно найти число, которое при возведении в третью степень дает 64.
Извлечь корень из числа на калькуляторе
Конечно, лучший способ научиться извлекать квадратные, кубические и другие степенные корни — это практиковаться, решать много примеров и запоминать таблицу квадратов и кубов небольших чисел. Это сделает решение уравнений в будущем очень простым и менее трудоемким. Однако следует отметить, что иногда необходимо извлечь корень из числа, которое настолько велико, что получить правильный квадрат числа было бы очень трудно, если не невозможно. Для помощи в извлечении квадратного корня используется простой калькулятор. Как использовать калькулятор для извлечения квадратного корня? Вы просто вводите число, от которого хотите найти результат. Теперь внимательно рассмотрите клавиши на калькуляторе. Даже в самой простой версии есть ключ с корневым символом. Если вы нажмете на него, то сразу же получите результат.
Не каждое число можно извлечь в виде целочисленного корня, см. следующий пример:
Корень из 1859 = 43.116122….
Вы можете попробовать решить этот пример одновременно с калькулятором. Как видите, полученное число не является целым; более того, набор цифр после десятичной точки не является конечным. Специальные механические калькуляторы могут дать вам более точный результат; обычные калькуляторы просто не показывают полный результат. И если вы продолжите в порядке квадратов, вы не найдете 1859, потому что число, которое вы возвели в квадрат, чтобы получить его, не является целым числом.
Если вы хотите извлечь корень третьей степени на простом калькуляторе, вам нужно дважды нажать клавишу с символом корня. В качестве примера возьмем число 1859, использованное выше, и извлечем его кубический корень:
Корень 3 из 1859 = 6.5662867….
То есть, если число 6.5662867…. возводится в третью степень, результат равен примерно 1859 г. Таким образом, извлечение корней из чисел не представляет сложности, если помнить приведенные выше алгоритмы.