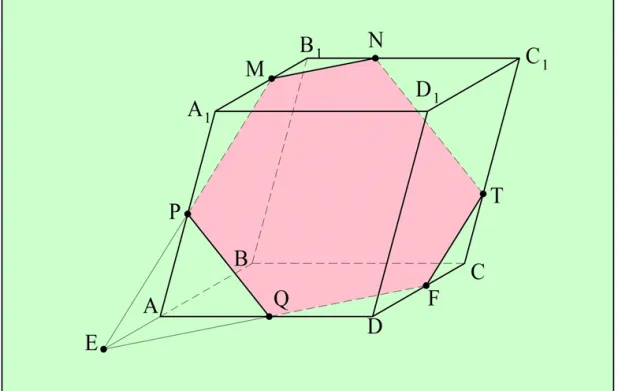
Прямоугольная система координат может использоваться в любом конечномерном пространстве так же, как и в трехмерном. Количество координатных осей в этом случае равно размерности пространства (в данном разделе она обозначается n).
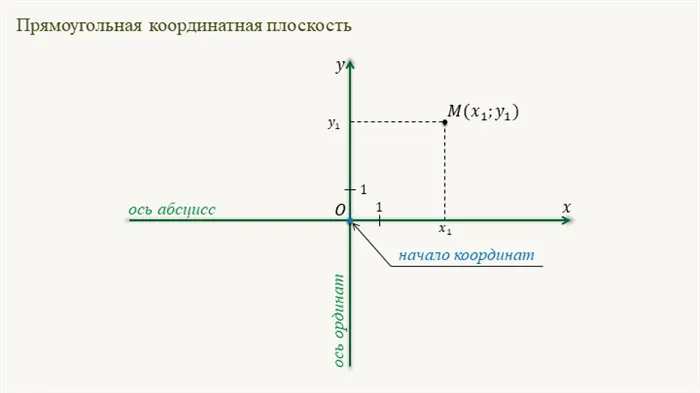
Прямоугольная система координат
Прямоугольная система координат — это прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Это самая простая и поэтому наиболее часто используемая система координат. Он очень прост и непосредственно обобщается на пространства любого размера, что также способствует его широкому применению.
Связанные термины: Декартовой системой координат обычно называют прямоугольную систему координат с одинаковым масштабом по осям, в то время как общая декартова система координат является аффинной системой координат (не прямоугольной) 1 .
Прямоугольная система координат на плоскости образована двумя координатными осями, перпендикулярными друг другу. Координатные оси пересекаются в точке
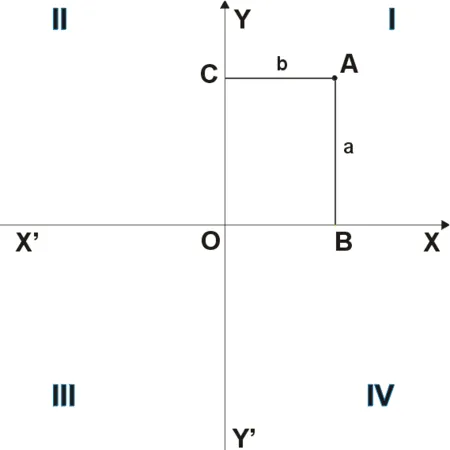

Положение точки и длина отрезка в каждом случае равны.
В этом случае координата находится на радиусе, как показано на рисунке). Координата лежит на линии.
Координата на луче — дистальное положение точки — линия точки.
Напишите это символически таким образом:
или указывает на координату, принадлежащую определенной точке, с помощью указателя:
- В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси смотрела направо. Обычно принято пользоваться правосторонними системами координат (если обратное не оговорено или не очевидно — например, из чертежа; иногда по каким-то соображениям бывает удобнее всё же пользоваться левосторонней системой координат).
- Четыре угла (I, II, III, IV), образованные осями координат квадрантами (см. рис. 1).
- Если точка имеет положительные абсциссу и ординату. Если точка имеет отрицательную абсциссу и положительную ординату. Если точка имеет отрицательные абсциссу и ординату. Если точка имеет положительную абсциссу и отрицательную ординату.
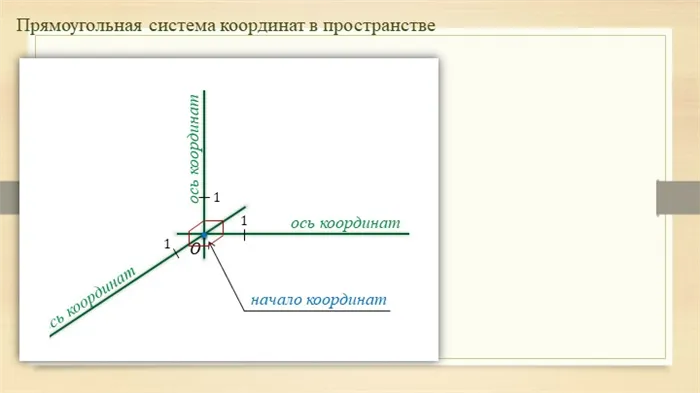
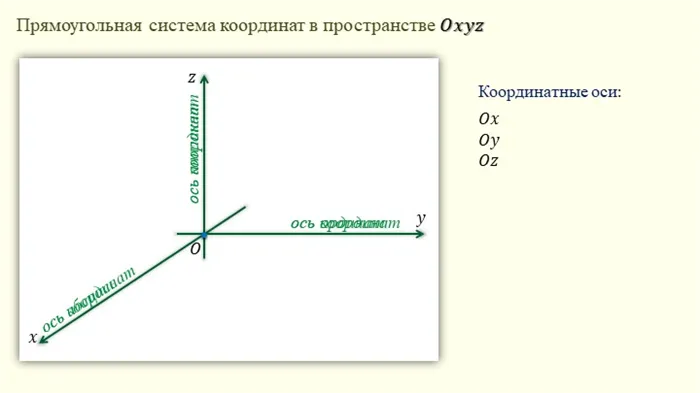
Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве (этот параграф относится к трехмерному пространству, о многомерном пространстве см. ниже) состоит из трех координатных осей, перпендикулярных друг другу и, называемой началом координат, с положительным направлением на каждой оси, обозначенным стрелками, и единицей измерения отрезков на осях. Единицы измерения обычно (не обязательно 2 ) одинаковы для всех осей; — упорядоченная ось,
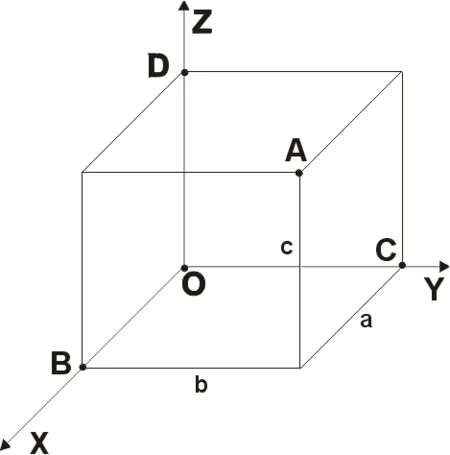
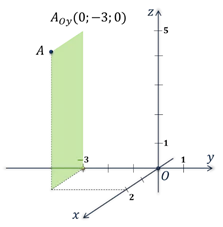
положение точки ,. Координаты, Координаты, Координаты в выбранных единицах измерения. Сегменты и и и
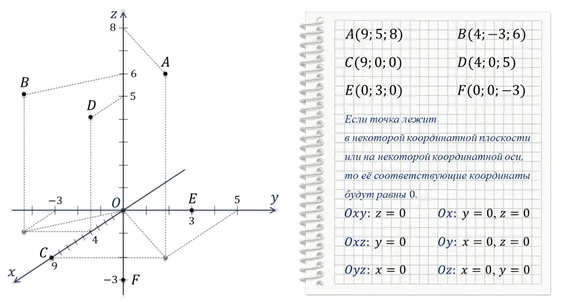
Координата, координата — упорядоченная точка — применение точки.
Символически это записывается следующим образом
или привязать запись координат к конкретной точке через указатель:
Каждая ось рассматривается как числовая прямая, т.е. имеет положительное направление, а точкам на отрицательном радиусе присваиваются отрицательные значения координат (расстояние обозначается знаком минус). То есть, если, например, точка, а в ее континууме в противоположном направлении от точки будет отрицательное (минус расстояние
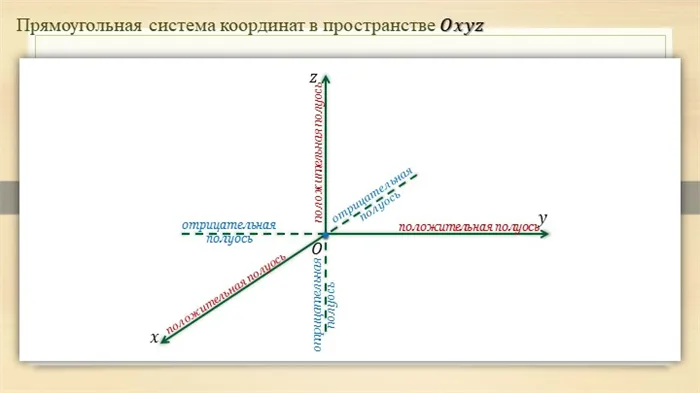
Ортогонально все системы координат в трехмерном пространстве делятся на две категории — по часовой стрелке (термины положительные, стандартные) и против часовой стрелки. Обычно по умолчанию стараются использовать правосторонние системы координат и по возможности размещать их в одном из нескольких обычных (традиционных) положений в графическом представлении. (На рисунке 2 показана правая система координат). Правую и левую системы координат нельзя выровнять поворотами 3 так, чтобы их соответствующие оси (и их направления) совпадали. Порядок данной системы координат может быть определен с помощью правила правой руки, правила винта и т.д. (положительное направление оси выбирается так, чтобы при вращении оси это вращение наблюдалось с положительного направления оси).
Прямоугольная система координат в пространстве презентация к уроку по геометрии (11 класс) по теме
Данная презентация может быть использована на уроках геометрии в 11 классе. В нем представлен справочный материал, описана тема «Прямоугольная система координат» и рассмотрены задачи.
О Леонгарде Эйлере можно рассказать, что он является швейцарским, немецким и русским ученым. Потому что он долгое время работал и в Германии, и в России, но родился в Швейцарии.
Работу выполнила учитель математики Острожской Нохриной Т.А.
Они уже знакомы с прямоугольной (декартовой) системой координат на плоскости, введенной в XIX веке французским математиком Рене Декартом.
С другой стороны, прямоугольная система координат в пространстве была введена швейцарским, немецким и русским математиком Леонгардом Эйлером в XVIII веке.
Работайте с книгой — Прочитайте первый абзац на странице 102.
Определите точку в пространстве и проведите из нее три перпендикулярные линии. Укажите направление стрелкой и выберите единицу измерения для каждой оси (используйте чертежную доску и тетрадь).
y X z o k i j Ось действия Ось нормальных осей Ось присоединенных осей.
Запишем в тетради: OX — ось вершин OY — ось ординат OZ — ось яблок i, j, k — единицы измерения (векторы координат) O — начало координат.
— Помните ли вы, что определяет положение точки на плоскости? Пример: M(3;7)
— Аналогично ответьте на вопрос «Что определяет положение точки в пространстве?». Пример: M(3;7;5)
Работа по учебнику стр. 102 Прочитаем параграф 3 Рассмотрим рисунок 122.
Координаты точки в пространстве M (M 1,M 2,M 3).
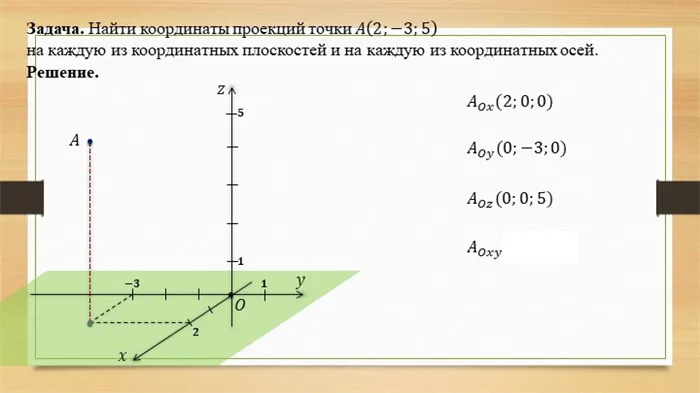
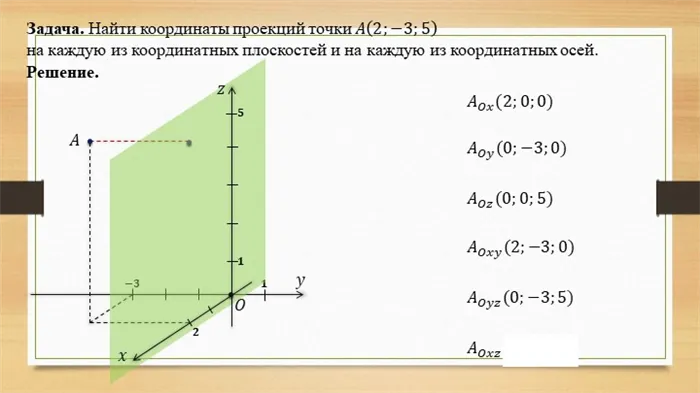
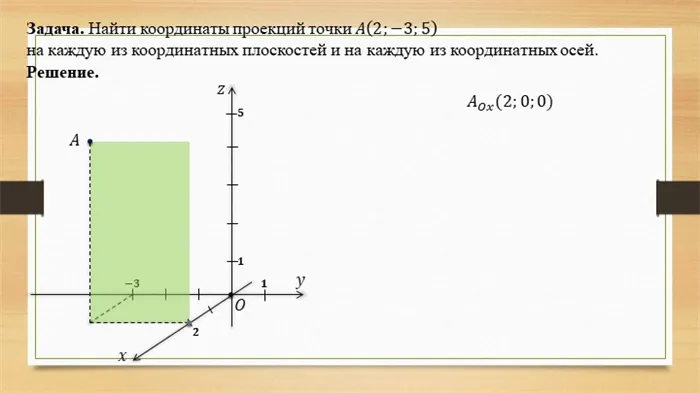
Таким образом:- Чтобы определить координаты точки в пространстве, нужно провести плоскости, параллельные осям, проходящим через точку.
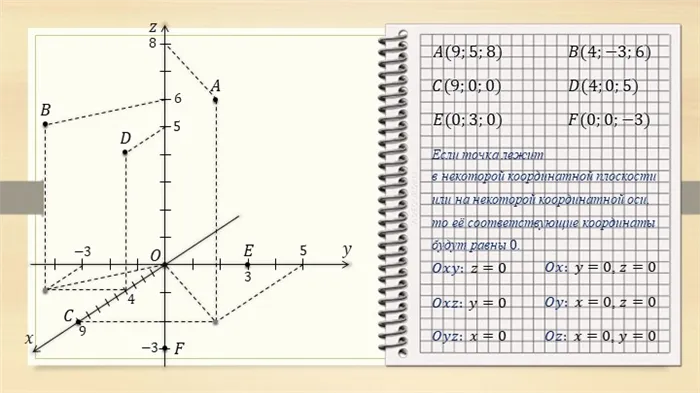
Если M OXU, то z=0 Если M OXZ, то y=0 Если M O U Z, то x=0 Если M OX, то y=0 и z=0 Если M O U, то x=0 и z=0 Если M OZ, то x=0 и y=0 Если M OZ, то x=0 и y=0 Если M OZ, то x=0 и y=0
Удалить (Геометрия 10-11 Л.С. Атанасян и другие, 2011) #400 #401 a #402
№ 400 Ответ: a) C(2;0;0) b) E(0;-1;0) C(0;0;-7) d) A(3;-1;0) e) G(0;5;-7) f) D (-4;0;3)
№ 401 (a) Ответ: a) A 1 (2;0;5), B 1 (3;0;1/2), C 1 (- ;0; — ) A 2 (2;-3;0), B 2 (3-5;0), C 2 (- ;- /2;0) A 3 (0;-3;5), B 3( 0;-5;1/2), C 3 (- ;- /2;0)
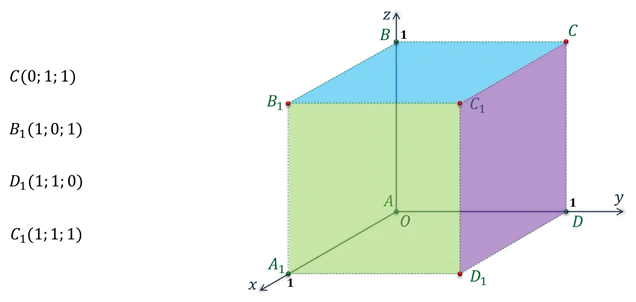
Нет. 402 Дано: A(0;0;0) B(0;0;1) D(0;1;0) A 1 (1;0;0) Найдено: B 1, D 1, C, C 1 Ответ: B 1 (1;0;1), D 1 (1;1;0), C 1 (0;1;1)
Домашнее задание: параграф 46, № 401(b).
Источники: Школьный учебник «Геометрия 10-11» Л.С. Атанасяна, 2011 http://ru.wikipedia.org
По теме: методические разработки, презентации и конспекты
Прямоугольная система координат. Векторы в пространстве. Векторные координаты.
Понятие прямоугольной системы координат, векторные координаты.
Прямоугольная система координат. Векторы в пространстве. Векторные координаты.
Понятие прямоугольной системы координат, векторные координаты.
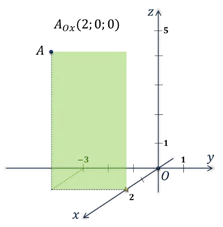
Чертеж прямоугольной системы координат /Rectangular Coordinate System/.
Задание «Прямоугольная система координат» для учащихся 6 класса.
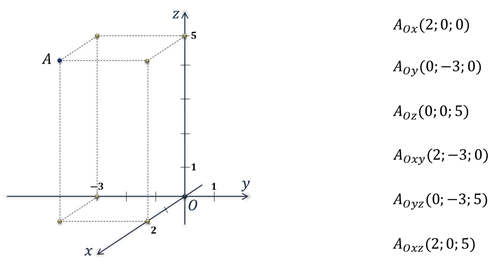
Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве.
Обзор урока геометрии для 11 класса «Прямоугольная система координат в пространстве».
Эскиз урока геометрии в 11 классе «Прямоугольная система координат в пространстве».
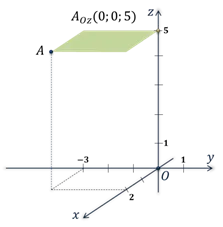
Презентация к уроку геометрии в 11 классе «Прямоугольная система координат в пространстве».
презентация может быть использована при объяснении новой темы и решении проблем.
Обзор урока «Прямоугольная (декартова) система координат в пространстве».
Раздел 3. ГеометрияТема 3.5 Координаты и векторыРабота 24. Прямоугольная (декартова) система координат в пространстве Цель урока: Учащиеся должны расширить свои знания о прямоугольной системе координат.
Прямоугольная система координат в пространстве

Значительное количество задач стереометрии можно легче решить с помощью метода координат. На этом уроке учащиеся изучат основные понятия прямоугольной системы координат в пространстве: Начало координат, координатная ось и координатная плоскость. Они также узнают, как определить координаты точки в пространстве.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам из комплекта, вам необходимо добавить его в свой личный кабинет.


2. распространить видеоуроки в личных учебных пространствах учащихся.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Прямоугольная система координат в пространстве»
Они уже знают прямоугольную систему координат на плоскости, т.е. прямоугольную координатную плоскость. Эта система координатопределяется двумя линиями, перпендикулярными друг другукаждый из которых имеет определенное направление…Направлениеистоимость единичного сегмента. Эти линии называются осями абсцисс и ординат.
Точка пересечения осей называется исходной точкой.
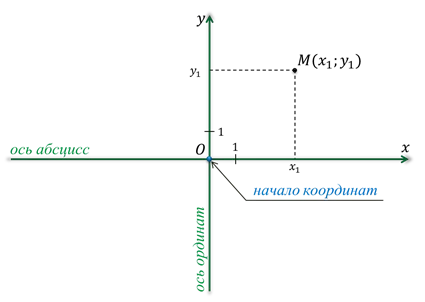
Прямоугольная система координат на плоскости называется Оху.
Каждая точка на плоскости имеет только одну пару чисел, которые называются координатами. Чтобы найти координаты, нужно провести перпендикуляр из точки к осям так, чтобы получились дисталь и диагональ точки.
Определение:
Если через точку в пространстве и направление проходят три попарно перпендикулярные прямые, и в каждой из них выбран единичный отрезок, то говорят, что задана прямоугольная система координат в пространстве.
Линии, на которых лежат выбранные направления, называются координатными осями, а точка их пересечения — началом координат, обычно обозначается буквой O, как на плоскости.
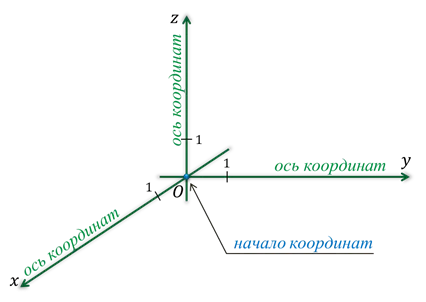
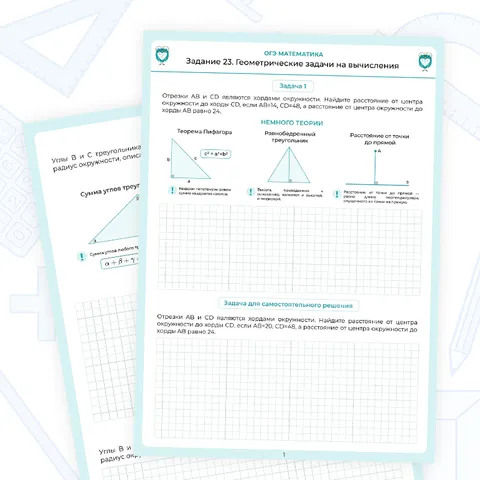
Координатные оси обозначаются как Oh, O и Oz. Они называются ось вершин, нормальная ось и — новое название для третьей оси — ось приложения.
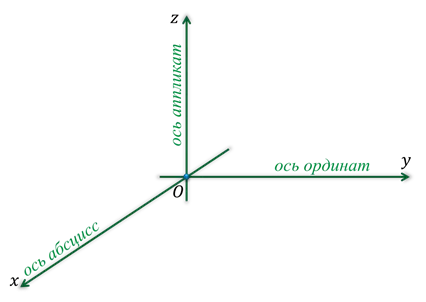
Прямоугольная система координат в пространстве называется Охуз.
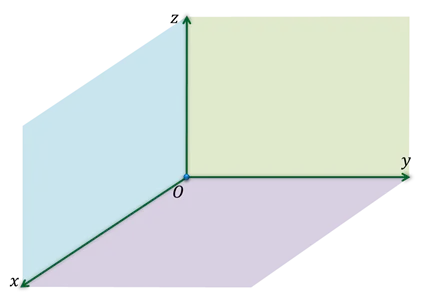
Координатные плоскости проходят через каждую из 2 координатных осей: оху, оц и оц. Всего существует 3 таких самолета.
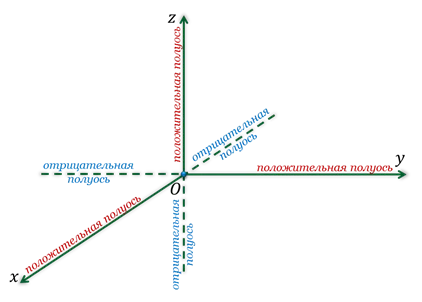
Каждая ось делится на два радиуса точкой O. Лучи, направление которых совпадает с направлением оси, называются положительными полуосями, а остальные лучи — отрицательными полуосями.
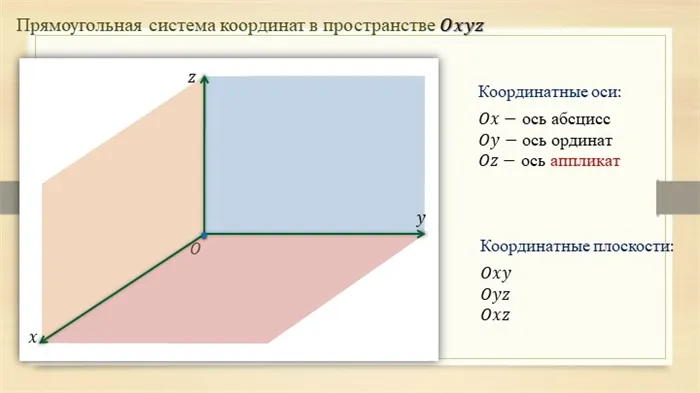
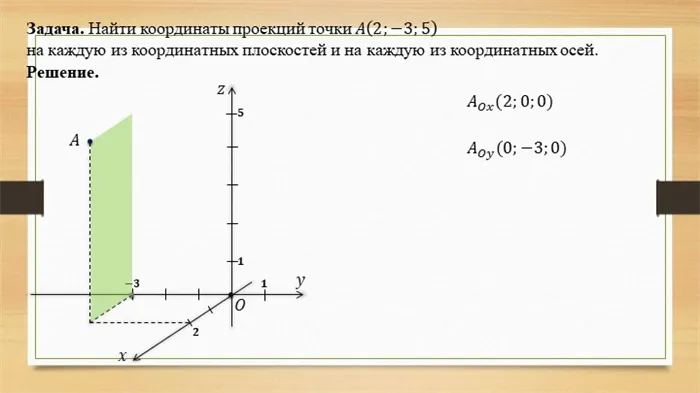
Каждая точка в пространстве имеет только один ряд чисел — координаты. Они определяются так же, как и на плоскости. Только через точку M проведены плоскости, перпендикулярные координатным осям.
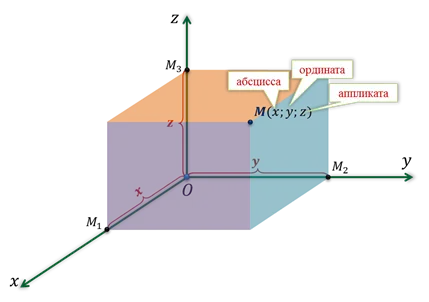
Пересечения нарисованных плоскостей с координатными осями называются M1, М2и М3.
Первая координата точки M, т.е. ее параметр, равна длине отрезка OM1.
Вторая координата, называемая упорядоченной координатой, равна длине отрезка OM.2.
А третья координата, называемая аппликатой, равна длине отрезка OM3.
Координаты точки записываются в скобках, первая — дистальное положение, вторая — ортогональное положение, третья — аппликативное положение.
Координаты середины отрезка
Пусть в пространстве существует отрезок AB и известны координаты его краев. Точка M является центром этого отрезка. Как можно вычислить его координаты? Рассмотрим связь между векторами AM, MV и AB:

Поскольку M — середина AB, векторы AM и MB имеют равную длину и лежат на одной прямой. Поэтому эти векторы равны и, следовательно, имеют одинаковую ковариацию:
Аналогичные формулы для координат y и z могут быть получены аналогичным образом:
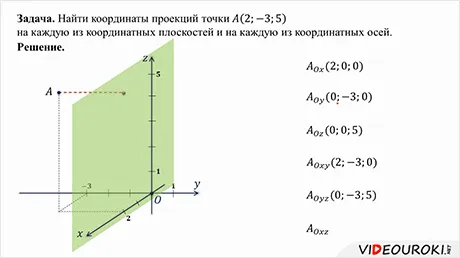
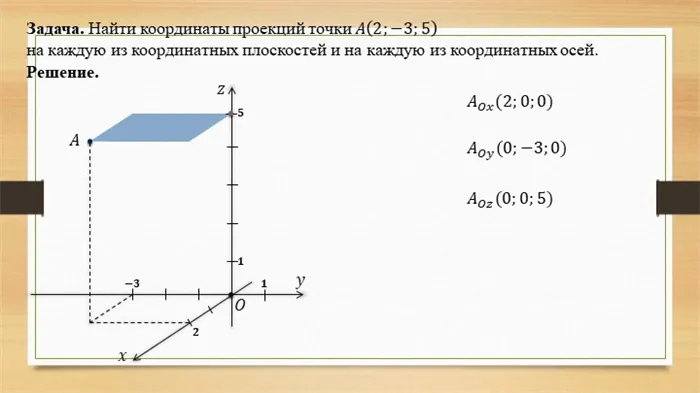
Рассмотрим некоторые задачи, связанные с координатами точек.
Проблема. Определите координаты середины отрезка, соединяющего отрезки A(3; 7; 12) и B(1; 5; — 4).
Решение. Просто используйте только что выведенные формулы. Средняя точка также задается буквой M:
Задание. K — средняя точка отрезка CD. Укажите координаты точек C и K: C(12; 9; — 3) и K(15; 7; 3), определите координаты D.
Решение. Сначала напишите формулу для координаты x:

Вычисление длины векторов и расстояния между точками
Рассмотрим вектор радиуса OM с координатами. Давайте попробуем определить его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор является диагональю:
Напомним, что квадрат длины диагоналей параллелепипеда равен сумме квадратов его диаметров. Но в полученном параллелограмме размерами являются координаты x, y и z, поэтому мы можем написать:
Поскольку равные векторы имеют и одинаковые координаты, и одинаковую длину, то ясно, что любой вектор с координатами равен рассматриваемому радиус-вектору, и поэтому его длина вычисляется по той же формуле.
Задание. Найдите длину вектора m.
Решение. Просто воспользуйтесь формулой:
Рассмотрим отрезок AB с известными координатами его ребер. Мы можем построить вектор AB и его координаты определяются следующим образом:

Задание. Найдите расстояние между K(10; 15; 5) и M(16; 21; — 2).
Решение. Просто введите координаты точек в формулу:
Проблема. Найдите длину медианы KM из ∆ KPN, если известны координаты вершин P(2; 5; 8), N(6; 9; 12) и K(16; 11; 13).
Решение. Чтобы определить длину медианы, достаточно знать координаты краев. Координаты K уже известны, а M — медиана PN, поэтому мы также можем вычислить ее координаты:
Коллинеарность векторов
Напомним, что если два вектора a и b коллинеарны, то должно существовать число k, для которого выполняется условие.
Полученное соотношение (1) является одновременно точкой липких векторов и их свойством. Слово «знак» означает, что все векторы, координаты которых удовлетворяют условию (1), коллинеарны. Слово «свойство» означает обратное — если мы знаем, что векторы коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике можно использовать фразу «тогда и только тогда»:
Очень важно, что это правило применимо только в том случае, если все координаты векторов ненулевые. Теперь рассмотрим случай, когда некоторые координаты вектора b (одна или две) равны нулю. Например
Из этого следует, что если функция вектора равна нулю, то любой вектор, присоединенный к нему, также должен быть нулевым. Особым случаем является случай нулевого вектора с координатами, который обычно предполагается коллинеарным с любым вектором.
Проект. Выясните, какая из этих пар векторов коллинеарна:
Решение. В первой задаче просто разделите соответствующие координаты и найдите значение коэффициента k:
Оказывается, что значение коэффициента k одинаково для каждой пары coord-t, поэтому векторы коллинеарны.
Повторите те же действия, что и в задаче b):
На этот раз коэффициенты k разные, поэтому векторы не коллинеарны.
В задаче c) вектор e имеет координату z ноль. Это означает, что если вектор f коллинеарен с z, то эта координата также должна быть равна нулю, но это не так. Поэтому векторы e и f не являются концентрическими.
В задаче г) снова даны векторы с нулевыми координатами. Однако оба вектора имеют нулевую координату z, поэтому они могут быть коллинеарны. Однако необходимо проверить, равно ли отношение ненулевых координат:
Отношение k равно, поэтому векторы коллинеарны.
В последней задаче д) вектор n равен нулю, так как все его координаты равны нулю. Нулевой вектор всегда коллинеарен с другими векторами, так и в этой задаче.
Ответ: а) да, б) нет, в) нет, г) да, д) да.
Задание. Определите, лежат ли точки A(3; 5; 12), B(5; 7; 16) и C(0; 2; 6) на одной прямой.
Решение. Если эти точки лежат на одной прямой, то векторы AB и BG коллинеарны. Если эти векторы не коллинеарны, то точки должны лежать на разных прямых.
Сначала вычислите координаты векторов AB и BC:
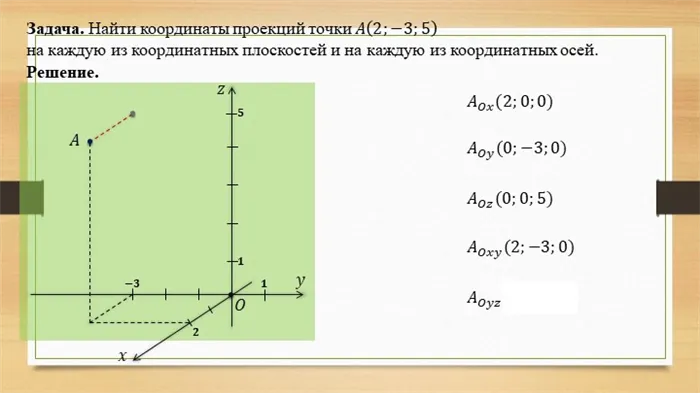
Теперь проверьте, коллинеарны ли эти векторы:
Коэффициенты k равны, и поэтому AB и BC — коллинеарные векторы. Поэтому точки A, B и C лежат на одной прямой.
Прямоугольные координаты вектора
Для определения ортогональных координат 6 .
- Таким образом, например, координаты (x,y) на рис.1 являются координатами вектора>» width=»» height=»» />.
Для векторов (направленных отрезков), начало которых не совпадает с началом координат, ортогональные координаты могут быть определены одним из следующих двух способов:
=a_+b_,>» width=»» height=»» />,c\ a_,\dots ,c\ a_)>» width=»» height=»» />