Сечение тетраэдра по трем точкам. Сечение тетраэдра по трем точкам.

Содержание

194923 194934 194909 194918 194947 194943 194922 194944 194919 194910 194935 194941 194929 194940 194949 194951 194907 194945 194946 194942 194913 194950 194933 194936 194912 194911 194932 194906 194948 194930

Тетраэдр

Пусть M, H, K — точки в пространстве, которые образуют ∆MNC и тем самым определяют плоскость. Отметьте другую точку P в пространстве, которая НЕ находится в плоскости МНК. Если мы соединим P с вершинами ∆MNC, то получим трехмерную фигуру. Он называется тетраэдром. Можно дать много различных определений тетраэдра, но мы ограничимся следующим:

Это название связано с тем, что в древнегреческом языке слово «тетра» означает «четыре». Тетраэдр имеет ровно четыре грани и ровно четыре вершины. Вот пример тетраэдра:

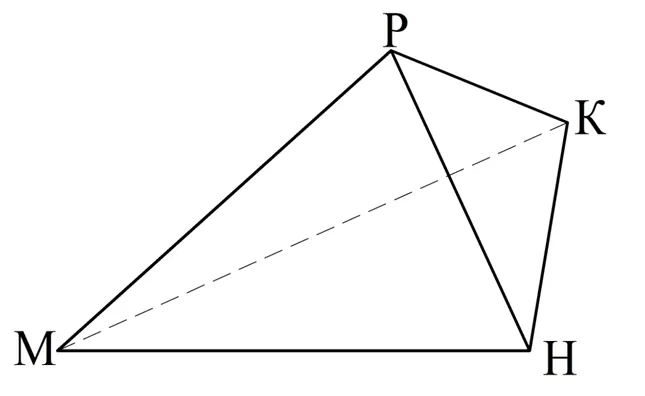
Легко видеть, что гранями тетраэдра являются треугольники, в данном случае это ∆MRN, ∆MKR, ∆MNC и ∆RKN. Иногда одна из граней выделяется особо и называется основанием тетраэдра. В этом случае три другие грани называются боковыми гранями тетраэдра.

Легко заметить, что у тетраэдра всего 6 граней. Поэтому назовем ∆MKH основанием тетраэдра. Как и любой треугольник, он имеет 3 стороны. Три других ребра — это отрезки, соединяющие каждую из трех вершин ∆MCH с точкой P. Перечислим лица, изображенные на рисунке: MK, KN, MN, MR, HP и KR.

Обратите внимание, что каждое ребро пересекает четыре других ребра и только одно ребро пересекает другое. Пары ребер, которые пересекаются, называются противоположными ребрами. Ребра RK и MN, MK и RN, MR и KN противоположны друг другу.

Тетраэдр называют простейшим многогранником. Это потому, что у него только 4 вершины, а многогранник не может иметь меньшее число вершин (потому что все три точки лежат в плоскости). В этом отношении тетраэдр очень похож на треугольник, самый простой из всех многоугольников. Как и треугольник, тетраэдр является очень жесткой конструкцией, поэтому он часто используется в технике. Тетраэдр также встречается во многих научных дисциплинах, включая физику. Например, кристаллическая решетка алмаза, самого твердого материала на земле, состоит из множества тетраэдров.

Наконец, следует отметить, что существует особый, так называемый нормальный тетраэдр. Его особенность заключается в том, что все его края имеют одинаковую длину.

Рассмотрим некоторые проблемы.

Задание. Известно, что в тетраэдре ABC есть буква D:

Найдите длины ребер AB, BC и AC этого тетраэдра и площадь ∆ABC. Округлите ответы до целых чисел.

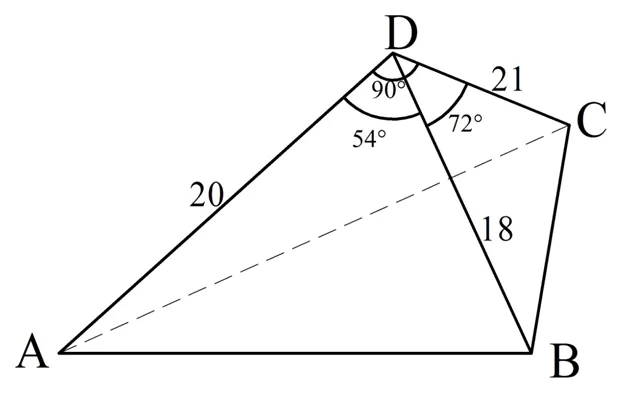
Неизвестные стороны можно вычислить, применив теорему косинусов к каждой стороне четырехугольника. Напишите его для ∆ADB:

Затем мы используем ∆ADC. Поскольку ∠ADC = 90°, мы можем записать частный случай теоремы Пифагора вместо теоремы косинусов:

Осталось найти площадь ∆ADC. Поскольку мы знаем длины всех сторон, проще воспользоваться формулой Герона. Помните, что для его использования необходимо сначала вычислить полукруглый периметр треугольника:

Параллелепипед

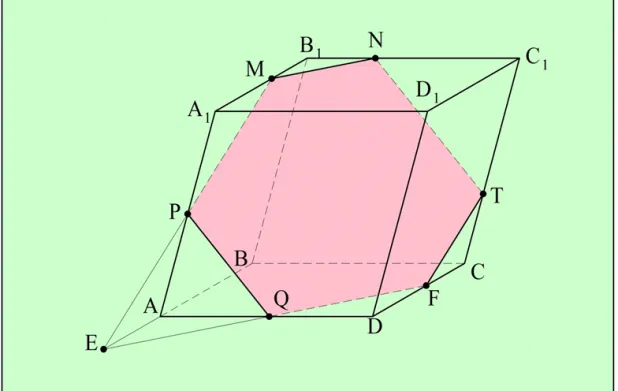
Построим параллелограмм ABCD на плоскости. Затем проведите через каждую вершину параллелограмма прямые, которые пересекаются и параллельны плоскости. Для каждой из этих линий определите точки A₁, В₁, С₁и D₁такие, что все они пересекают плоскость ABCD и равенство выполняется:

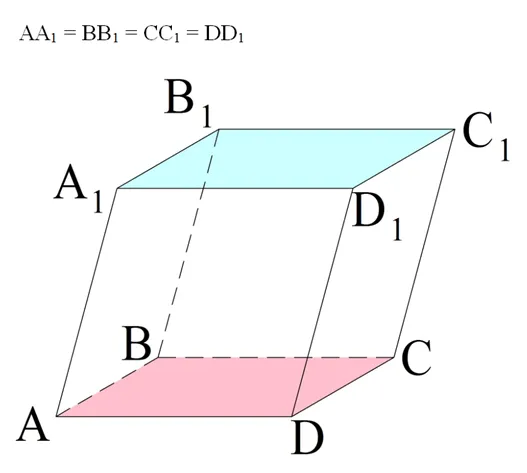
Обратите внимание, что в этом случае квадраты AA.₁D₁Д, АББ₁А₁BCC₁В₁и CDD₁C₁являются параллелограммами, так как две противоположные стороны каждого из них равны и параллельны. Также видно, что сегменты A₁D₁и Б₁С₁также параллельны и тождественны по свойству транзитивности:

Это означает, что оба A₁D₁C₁B₁— параллелограмм. Получается, что нам удалось построить многогранник с 6 гранями, каждая из которых является параллелограммом. Такой многогранник называется параллелограммом.

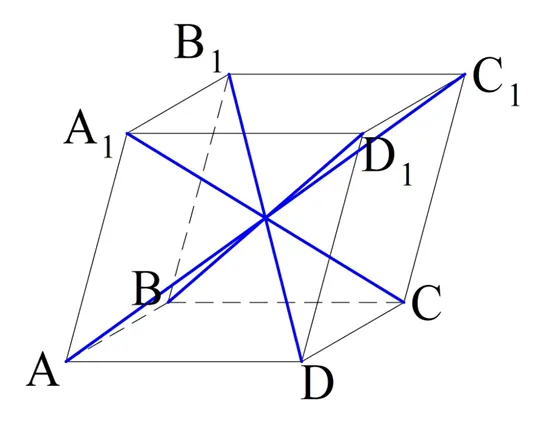
Легко вычислить, что параллелограмм имеет ровно 8 вершин и 12 ребер. Если грани параллелограмма имеют общее ребро, они называются смежными. В противном случае лица называются противоположными. Вершины параллелепипеда также могут находиться напротив друг друга, если они не лежат на одной грани. Таким образом, в приведенном выше примере вершины A и C являются₁, B и D₁С и А₁Д и Б₁.

Существуют также диагонали параллелепипеда. Это линии, соединяющие противоположные угловые точки:

Иногда на параллелепипеде выбираются две противоположные грани, которые называются основаниями параллелепипеда. В этом случае остальные четыре грани называются боковыми.

Сформулируем важное свойство параллелограмма.

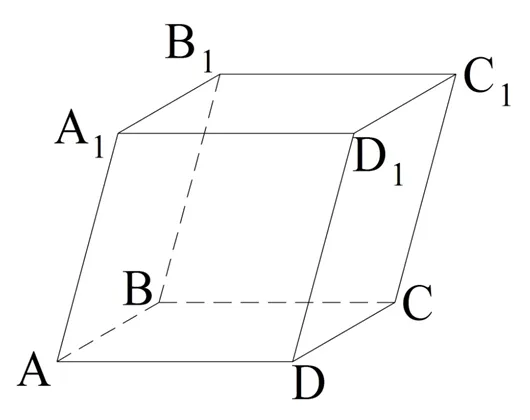
Рассмотрим параллелограмм ABCDA₁В₁С₁D₁:

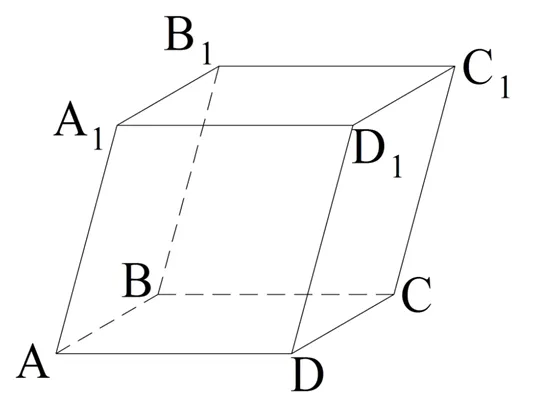
Давайте сравним лица ABB₁А₁и CDD .₁C₁. СD||ВВВВ как грани параллелограмма ABCD и DD.₁||А₁A как стороны параллелограмма AA₁D₁D. Из параллельности плоскостей следует, что грани ABB₁А₁и CDD .₁C₁параллельны, так как содержат пересекающиеся прямые (СD и DD₁в CDD₁C₁AB и AA₁в АББ₁А₁), которые попарно расположены параллельно друг другу.

Теперь мы хотим доказать, что эти ребра также равны. Отрезки AB и CD равны, потому что они являются частью параллелограмма ABCD. По той же причине отрезки AB₁и ДД₁(которые находятся в другом параллелограмме, AA₁D₁D): также идентичны ∠CDD₁и ∠BAA₁так как эти углы имеют стороны, которые являются лучами одного направления. Равенство двух сторон и угла между ними достаточно для доказательства равенства параллелограммов ABB₁А₁и CDD .₁C₁, h, и т.д.

Построение сечений

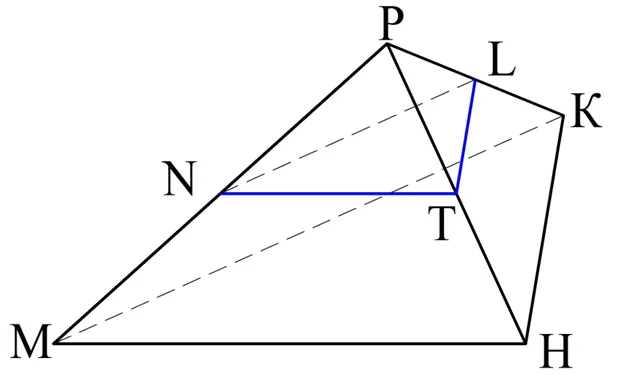
Любую трехмерную форму можно «разделить» на две части обычным способом, проведя через нее плоскость. Эта плоскость, проходящая через трехмерную форму, называется вторичной плоскостью.

В результате пересечения плоскости и трехмерной фигуры получается двухмерная фигура, которая называется пересечением. На рисунке выше сегментом является ∆NTL. Опять же, обратите внимание на разницу между терминами «вторичная плоскость» и «пересечение». Плоскость — это бесконечная форма, то есть она не имеет границ. Пересечение, с другой стороны, — это плоская фигура, имеющая границы. Одним из предметов, которым занимается стереометрия, является форма пересечений определенных фигур.

Плоскость пересечения пересекает каждую грань многогранника отрезком, концы которого находятся на гранях многогранника. Таким образом, пересечение тетраэдра, параллелепипеда и вообще любого многогранника — это плоский многоугольник. Тетраэдр имеет только 4 грани, поэтому его сегмент не может иметь более 4 сторон. Другими словами, пересечение тетраэдра — это либо четырехугольник, либо треугольник. Параллелограмм уже имеет шесть граней, поэтому его сегменты также могут быть прямыми шестиугольниками.

Важно уметь строить пересечения, зная лишь несколько общих точек трехмерной фигуры и вторичной плоскости. Для многогранников достаточно найти все общие точки вторичной плоскости и ребра, которые затем должны быть соединены отрезками. Обратите внимание, что каждая сторона отрезка должна лежать на одной из граней многогранника. Если мы не можем построить отрезок с этим ограничением, это означает, что отрезок пересекает какие-то другие грани многогранника, и нужно найти соответствующие точки пересечения. Давайте рассмотрим некоторые примеры задач по построению секций.

Задача. Постройте точку пересечения тетраэдра ABC D через точки M, N и P:

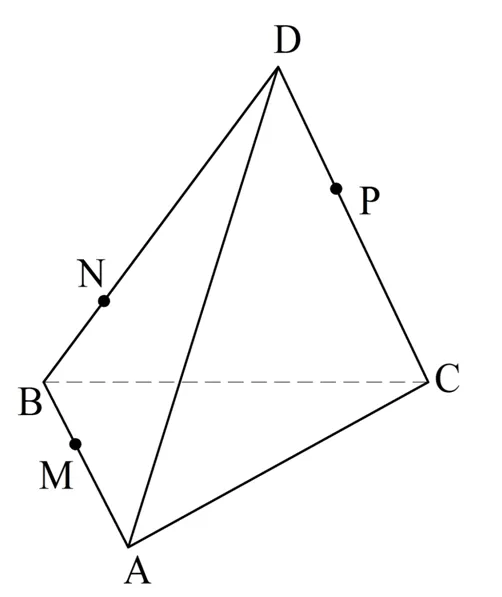
Решение. У нас уже есть три точки на ведомственной плоскости. Однако мы не можем просто соединить их, потому что точки M и P лежат на разных ребрах. Поэтому нам нужно найти другую общую точку отрезка, которая лежит на ребре.

Обратите внимание, что плоскость MNP имеет две общие точки с плоскостью BCD, а именно N и P. Это означает, что они пересекаются прямой NP. Это означает, что если линия BC пересекает NP, то точка пересечения находится во вторичной плоскости. Продолжая BC и NP, они пересекаются в точке E, которая, как мы только что видели, лежит во вторичной плоскости:

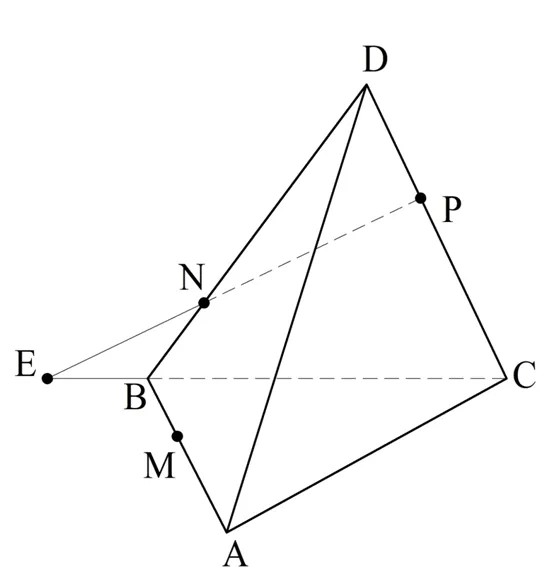
E лежит в BC, а BC является частью плоскости ABC. Следовательно, E лежит в плоскости ABC. С другой стороны, «М» также можно увидеть на канале ABC. Оказывается, что прямая EM имеет две точки, принадлежащие плоскости ABC, поэтому все они принадлежат ABC. Затем мы можем найти пересечение с линией AC, просто продлив линию EM:

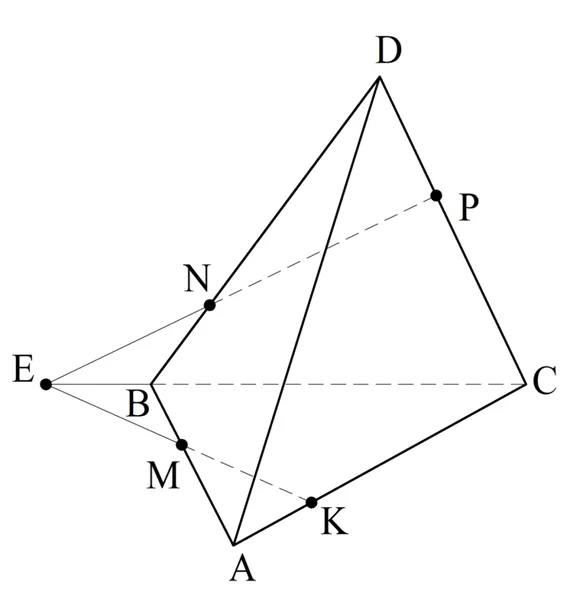
Здесь мы обозначим пересечение EM и AC через K. Таким образом, мы можем построить отрезок MNPK, так как каждая сторона этого многоугольника принадлежит одной из граней четырехугольника:

Презентация по теме «Построение сечений тетраэдра»

В настоящее время 54 270 учебных заведений имеют право на дополнительные накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.

Образовательный курс

Интерактивные технологии в обучении и воспитании

К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы InforoLesson).

Сейчас обучается 102 человека из 37 регионов

Образовательный курс

Система работы учителя математики по подготовке учащихся основной школы к математическим конкурсам и олимпиадам в рамках обновленного ФГОС ООО

Курс добавлен 26.10.2022
Сейчас обучается 42 человека из 25 регионов

«Формирование математической грамотности с целью развития общих компетенций»

Описание презентации по отдельным слайдам:

1 Слайд Построение четырехгранных сечений

2 слайда Содержание: пересмотр; введение; пересмотр; пересмотр; тесты с несколькими вариантами ответов (4 варианта) и анализ решений,

3 Слайд 3 A1 Одна плоскость проходит через три точки, не лежащие на одной прямой.

4 Слайд 4 A2 Если две точки на прямой лежат в плоскости, то вся прямая лежит в этой плоскости.

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 990 696 материалов в базе данных

Другие материалы

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

Оставьте свой комментарий

Войдите в систему, чтобы задавать вопросы.

04.02.2016 6412
PPTX 3.9 мбайт
46 скачиваний
Рейтинг: 2 из 5
Оцените материал:

Если вы считаете, что материал нарушает авторские права или должен быть удален с сайта по любой другой причине, вы можете подать жалобу на материал. Удаление материала

Автор материала

На сайте: 9 лет и 7 месяцев
Подписчики: 0
Всего просмотров: 87601
Всего материалов: 46

Скидка для новых слушателей. Зарегистрируйтесь, чтобы применить свою скидку к любому курсу

Задача 4

Дан тетраэдр ABC D. Точка M — внутренняя точка, конечная точка тетраэдра AB D. N — внутренняя точка отрезка D C (рисунок 6). Постройте точку пересечения прямой NM с плоскостью ABC.

Рисунок 6. Иллюстрация к задаче 4.

Решение: Для решения задачи построим вспомогательную плоскость D MN. Предположим, что прямая D M пересекает прямую AB в точке K (рис. 7). Тогда SC D — отрезок плоскости D MN и четырехугольника. И прямая NM, и полученная прямая SK лежат в плоскости D из MN. Поэтому, если NM не параллельна SK, то эти две прямые пересекаются в точке P. P — искомая точка пересечения прямой NM с плоскостью ABC .

Рисунок 7. Иллюстрация к задаче 4. решение задачи 4.

Задача 5 Построить сечение тетраэдра плоскостью

Дан тетраэдр ABC D. M является внутренней точкой грани ABC D. P — внутренняя точка ребра ABC. N — внутренняя точка ребра D C (рис. 8.). Постройте точку пересечения тетраэдра с плоскостью, проходящей через M, N и P .

Рисунок 8. Чертеж к заданию 5 Постройте пересечение тетраэдра с плоскостью.

Решение: Рассмотрим первый случай, когда прямая MN не параллельна плоскости ABC. В прошлой задаче мы нашли точку пересечения прямой MN с плоскостью ABC. Это точка K, которую мы получаем с помощью вспомогательной плоскости D MN, то есть проводим D M и получаем точку F. Затем строим CF и получаем точку K на пересечении MN.

Рис. 9. Задача 5: Нахождение точки K

Проведите линию K. RR лежит как в плоскости пересечения, так и в плоскости ABC. Таким образом, мы получаем точку P₁и P₂. Подключение P .₁и M и затем получить точку M .₁. Подключение P₂и N. Это дает требуемый отрезок P₁Р₂NМ₁. Проблема в первом случае решена. Рассмотрим второй случай, в котором прямая MN параллельна плоскости ABC. Плоскость MNP проходит через прямую MN, которая параллельна плоскости ABC, и пересекает плоскость ABC прямой P₁Р₂тогда линия P₁Р₂параллельна линии MN (рис. 10).

Читайте также: Как избежать санкций Google Play в Крыму.

Рисунок 10. иллюстрация проблемы 5. деталь, которую нужно найти.

Итоги урока по теме «Тетраэдр», «Ребро тетраэдра», «Грани тетраэдра», «Поверхность тетраэдра», «Вершины тетраэдра»

Итак, мы рассмотрели тетраэдр и решили несколько типичных задач с тетраэдром. В следующем уроке мы рассмотрим параллелепипед.

Список рекомендуемых материалов для чтения по тетраэдру. 1.

1. 1. И. М. Смирнова, В. А. Смирнов — 5-е переработанное и дополненное издание — М. : Мнемозина, 2008 — 288 с. Обзор современного состояния и новейших книг по геометрии : Мнемозина, 2008. геометрия. 10-11 класс. Учебник для учащихся общеобразовательных школ (начальный и профильный уровни) 2.

Шарыгин И.Ф. — М.: Дрофа, 1999. 208 Геометрия. 10-11 класс: учебник для учащихся общеобразовательных школ 3.

3 E. Потоскуев, Л. И. Звалич — 6-е издание, стереотипное — М.: Дрофа, 008 — 233 с. :syl. Геометрия. 10 класс: учебник для общеобразовательных учреждений с углубленным и профильным изучением математики.

Дополнительные интернет-ресурсы

1. сечения через четырехугольник (источник).

2. Как построить сечение через тетраэдр. Математика (источник).

3. фестиваль образовательных идей (источник).

Решите дома задачи на четырехугольники, как найти ребро четырехугольника, грани четырехугольника, вершины и поверхность четырехугольника.

1-я Геометрия. 10-11 классы: Учебник для учащихся общеобразовательных учреждений (базовый и профильный уровень) И. М. Смирнова, В. А. Смирнов — 5-е издание, переработанное и дополненное — М.: Мнемозина, 2008 — 288 с., иллюстр. Задачи 18, 19, 20 стр. 50

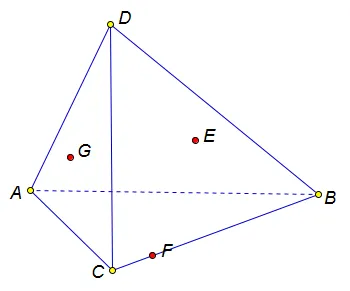
Точка E является центром ребра MA тетраэдра MABC. Постройте точку пересечения тетраэдра с плоскостью, проходящей через точки B, C и E.

3. В тетраэдре MABC точка M принадлежит ребру AMB, точка P — ребру BMC и точка K — ребру AC. Постройте точку пересечения тетраэдра с плоскостью, проходящей через точки M, P, K. 4.

4. Какие фигуры могут получиться в результате пересечения тетраэдра с плоскостью?

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.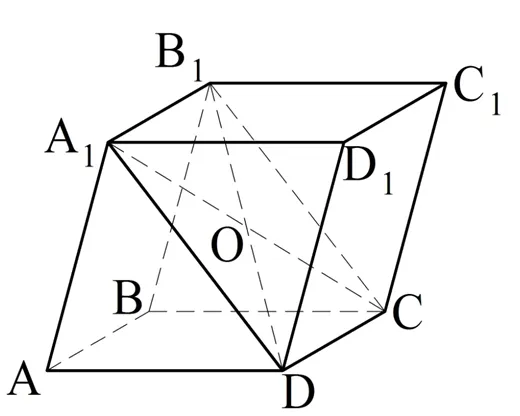

14(C2): Пересечение четырехугольника через три точки

Построить сечение тетраэдра SАВС через три точки K, M, N, лежащие соответственно на рёбрах АС, SC и SB.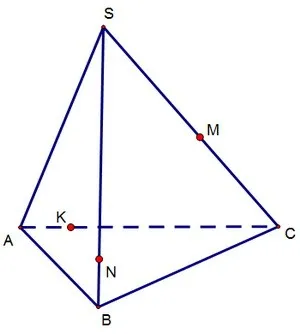Построим сечение методом следов. 1) Так как точки M и N лежат в правой грани, есть смысл их соединить и пересечь прямую MN с прямой СВ, лежащей в той же грани. Прямые пересекаются в точке Х, которая одновременно лежит и в правой грани, и в нижней. Само собой, эта точка лежит и в плоскости сечения.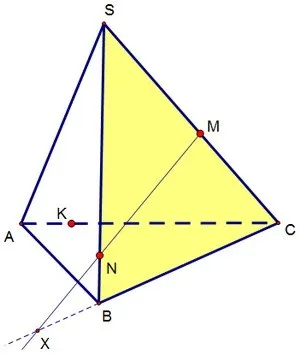2) Находясь теперь в нижней грани, пересечём прямые КХ и АВ. Получившаяся точка L лежит как в нижней, так и в левой гранях тетраэдра. Разумеется, она тоже является точкой сечения.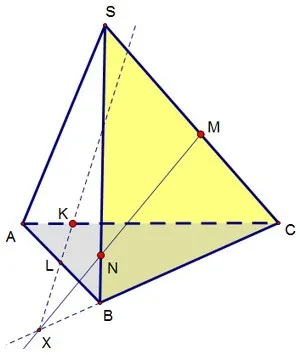3) Соединим теперь точки N и L в левой грани, а также точки К и М в задней грани. Получившийся четырёхугольник KLNM и есть искомое сечение.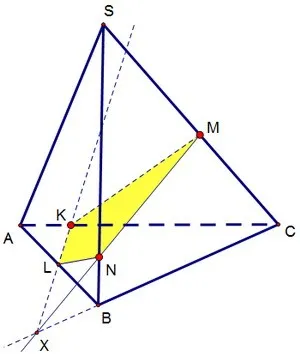

Автор.

Ольга Ольга Ольга Ольга: Ольга Залаченко, Ольга Залаченко:

Комментарий добавлен: Виктория Дата: 2014-11-23

Большое спасибо, очень полезно, добавил в два счета

Комментарий добавлен: Дата: 2018-12-07

Построить сечение тетраэдра через три точки. «Построение сечений тетраэдра и параллелепипеда. Построить точку пересечения прямой МN и плоскости BDC

Сегодня давайте еще раз рассмотрим, как построить пересечение четырехугольника с плоскостью. Рассмотрим простейший случай (обязательная плоскость), когда 2 точки плоскости пересечения принадлежат одному лицу, а третья точка — другому лицу.

Вспомните алгоритм построения сегментов такого типа (случай: 2 точки принадлежат одному лицу).

Найдите поверхность, содержащую две точки плоскости сечения. Проведите прямую через две точки на одном лице. Найдите точки пересечения с ребрами четырехугольника. Часть линии, которая содержится в грани, является стороной точки пересечения.

Если многоугольник может быть замкнут, то строится пересечение. Если многоугольник нельзя замкнуть, найдите точку пересечения построенной прямой с плоскостью, содержащей третью точку.

1. Видим, что точки E и F лежат в одной грани (BCD), проведем прямую EF в плоскости (BCD).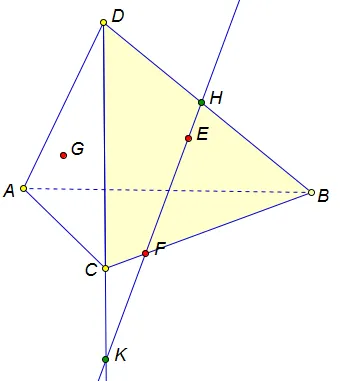2. Найдем точку пересечения прямой EF c ребром тетраэдра BD, это точка Н. 3. Теперь следует найти точку пересечения прямой EF и плоскости, содержащей третью точку G, т.е. плоскости (ADC). Прямая CD лежит в плоскостях (ADC) и (BDC), значит она пересекается с прямой EF, и точка К является точкой пересечения прямой EF и плоскости (ADC). 4. Далее находим еще две точки, лежащие в одной плоскости. Это точки G и K, обе лежат в плоскости левой боковой грани. Проводим прямую GK, отмечаем точки, в которых эта прямая пересекает ребра тетраэдра. Это точки M и L. 4. Осталось «замкнуть» сечение, т.е.соединить точки, лежащие в одной грани. Это точки M и H, и также L и F. Оба этих отрезка — невидимы, проводим их пунктиром.

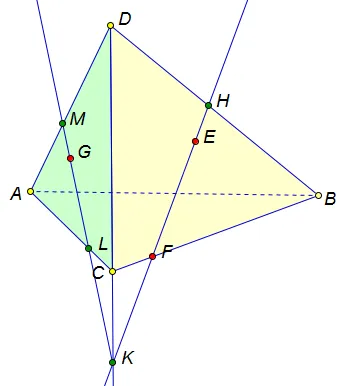
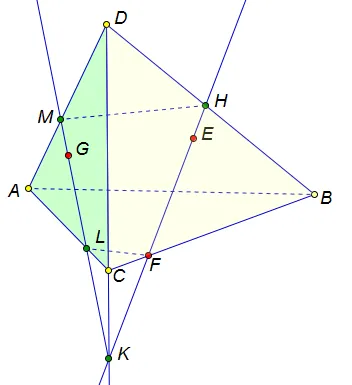
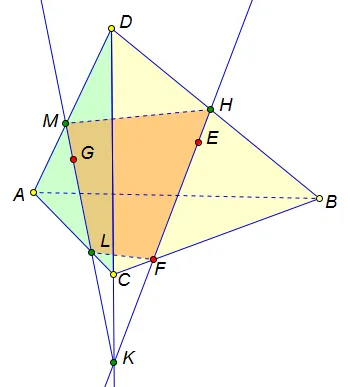
Пересечение заканчивается четырехугольником MHFL, все вершины которого лежат на ребрах четырехугольника. Выделим полученный сегмент.

Давайте теперь сформулируем «свойства» правильно построенного пересечения:

1. все вершины многоугольника, образующего пересечение, лежат на ребрах тетраэдра (параллелепипеда, многоугольника).

2. все стороны пересечения лежат на гранях многогранника. 3. каждая грань многогранника не может содержать более одной (одной или ни одной!) стороны отрезка.

Урок изучения нового материала.

Это урок с использованием ИКТ.

Геометрия: учебник для 10-11 классов / Л.С. Атанасян — М.: Просвещение, 2010,

Проспериченский, Просперический, Просперический, Просперический, Просперический.

Презентация PowerPoint,

Рисунки,

Работа в классе. Тема курса: Построение деталей тетраэдра. 29.10.

A B C D ТЕТРАЭДР — ДАВС Тетраэдр » tetra» — четыре, » hedra» — область.

Цель урока: Задачи урока: Развивать умение строить части тетраэдра с плоскостью, проходящей через три заданные точки. Содержание урока: — Введение в определение вторичной плоскости и пересечения тетраэдра с плоскостью; — Формулировка алгоритма для построения пересечения прямой с плоскостью; — Формулировка алгоритма для построения пересечения тетраэдра с плоскостью. Развитие: — продолжение развития пространственного воображения и математического мышления; — развитие аналитического мышления для разработки алгоритма построения пересечения прямой линии с плоскостью и пересечения многогранников. Воспитание: — развитие способности сознательно работать над поставленной целью; — продвижение культуры общения.

Развитие культуры общения. 1. если две параллельные плоскости пересекаются третьей плоскостью, то пересекающиеся прямые параллельны. 2. плоскость проходит через прямую и точку, не лежащую на ней, и только через одну. 3. если две различные плоскости имеют общую точку, то они пересекаются прямой, проходящей через эту точку. 4. если две точки на прямой лежат в плоскости, то все точки на прямой лежат в этой плоскости. 5. плоскость проходит через две пересекающиеся прямые и только через одну из них. A B C D E

Задача: Найдите пересечение прямой AB с плоскостью M NK .

Задание 2: Постройте прямые, проходящие через M, N, K .

Раздел A B C D M N K .

A B C D M N K a

A B C D M N K След — это пересечение плоскости сечения с плоскостью грани многогранника. MK — след от плоскости MNK до плоскости ABC MN … НК является …

Какие многоугольники можно получить в пересечении? Тетраэдр имеет 4 грани, которые могут создавать сечения: Четырехугольники Треугольники

Постройте пересечение тетраэдра с плоскостью через точки E, F, K. E F K L A B C D M 1. нарисовать K F. 2. нарисовать FE. 3. продолжить EF, продолжить AC. 5. переместить MK. 7. соедините EL EFKL, это необходимое сечение правила 6. MK AB=L 4. EF AC = M

Обратите внимание на следующее: 1. Можно соединить только две точки, лежащие в плоскости ребра. Для построения точки пересечения необходимо построить точки пересечения вторичной плоскости с ребрами и соединить их отрезками. 2 Если в плоскости поверхности, принадлежащей плоскости пересечения, отмечена только одна точка, необходимо построить еще одну точку. Для этого найдите точки пересечения уже построенных линий с другими линиями, принадлежащими тем же поверхностям.

Постройте точку пересечения тетраэдра с плоскостью, проходящей через точки E, F, K. 1 способ 2 способ

Вывод: Независимо от метода строительства, сегменты идентичны. Метод 1 Метод 2.

Проверьте правильность построения отрезка. Объясните ошибку.

A B C D N K M X P T Проверь себя Решение 1. KN = a ∩ DVS X = K N ∩ BC T = M X ∩ AB P = TX ∩ AC P T = a ∩ ABC, M є P T PN = a ∩ ADF TP N K — искомый отрезок.

Точка M — середина грани BC D четырехугольника DABC. Постройте точку пересечения этого четырехугольника с плоскостью, проходящей через точку M и параллельной плоскости AB D. К Д А К М К Л Н

Постройте сечение четырехугольника ABCD, проходящее через точку R и параллельное плоскости BCD. 2. Постройте сечение четырехугольника ABCD, проходящее через точку S и параллельное плоскости ABC. 3. Постройте сечение четырехугольника ABCD, проходящее через точку T и параллельное плоскости ACD. 4. Постройте сечение четырехугольника DABC, проходящее через точку M параллельно плоскости BC D.

Предварительный просмотр:

МБОУ «Кимовская средняя общеобразовательная школа

Спасский муниципальный район

«Построение четырехгранных профилей».

Евгения Геннадьевна Мамонова,

Учитель математики первой квалификационной категории

обеспечить в ходе урока усвоение алгоритма решения задач на построение сечений тетраэдра.
обеспечить усвоение понятий тетраэдра, систематизировать знания, связанные с аксиомами стереометрии, определениями, свойствами, понятием взаимного расположения точек, прямых и плоскостей в пространстве.
формировать навыки изображения рассматриваемых объектов на плоскости и “чтение” предлагаемых изображений, графической грамотности;
формировать умения применять приемы сравнения, обобщения, умозаключения.

развитие умения применять полученные знания по стереометрии на практике,
формирование умения анализировать и обобщать знания в процессе решения задач на построение сечений тетраэдра.
уметь выполнять различные вычисления, связанные с определением площади сечения.

воспитание осознанной потребности в знаниях,
совершенствование учебных умений и навыков,
воспитывать познавательный интерес к предмету через приобретение пространственного воображения и умения видеть красоту окружающего мира.

Урок изучения нового материала.

Это урок с использованием ИКТ.

Метод сравнения и обобщения.

Геометрия: учебник для 10-11 классов / Л.С. Атанасян — М.: Просвещение, 2010,

Проспериченский, Просперический, Просперический, Просперический, Просперический.

Презентация PowerPoint,

Рисунки,

Модели тетраэдров, кубоидов, кубоидов и кубов.

Орг. момент (1 мин).
Актуализация ранее приобретенных знаний (3 мин).
Подготовка к восприятию нового материала (3 мин).
Создание проблемной ситуации (3 мин).
Объяснение нового материала (10 мин).
Закрепление изученного материала (5 мин).
Самостоятельная работа с последующей проверкой (3 мин).
Практикум (5 мин).
Решение задачи (8 мин)
Это интересно (1 мин).
Постановка домашнего задания (1 мин).
Подведение итогов урока, рефлексия (2 мин).

Здравствуйте, дети. Садись.

«Я не думаю, что мы когда-либо жили в такой геометрический период, как сейчас. Все вокруг нас — геометрия». (Слайд 2) Эти слова великого французского архитектора Ле Корбюзье в начале двадцатого века очень точно описывают наше время. Мир, в котором мы живем, полон геометрических форм домов и дорог, гор и полей, творений природы и человека. Эта наука поможет вам лучше ориентироваться на местности, открывать для себя новое, понимать красоту и мудрость окружающего мира. Поэтому я приглашаю вас заняться геометрией с еще большим рвением.

Приветствие учителя. Садись.

2. Освежить уже полученные знания.

Устная работа. Вопросы:

О каком многограннике мы узнали на прошлом уроке?

Дайте определение тетраэдра.

Покажите элементы тетраэдра в модели.

Сегодняшняя тема — «Конструирование частей тетраэдра» (слайд 4). Отметьте тему в своих тетрадях.

Мы узнаем, какая плоскость называется вторичной, методы и приемы построения сечений, а также научимся строить сечения тетраэдра (слайд №5). В этом уроке вы будете работать с контурами и строить по ним сечения тетраэдра.