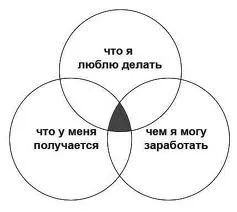
На изображении зеленый цвет является самым крупным и представляет общие игровые опции. Одним из них является Создатель (Голубой овал). Мейкер — это отдельное целое само по себе, но в то же время часть общей игры.
Круги Эйлера: что это и где применяются
Свободные авторы, специализирующиеся на написании статей о питании, кулинарии, доме и уходе за собой.
Сертифицированный педагог-психолог с более чем семилетним опытом работы в сфере совершенствования образования. Автор статей по педагогике и психологии.
Эйлерова окружность — это простая диаграмма, которая может быть использована для отображения взаимосвязи между общим и его частями. Это также помогает увидеть логическую цепочку между явлениями и понятиями.
Метод Эйлера используется для упрощения задач во многих областях, от математики до управления. Он помогает находить ответы, создавая четкие логические цепочки.
Леонгард Эйлер (1707-1783) был швейцарским математиком, физиком, инженером и философом. Он долгое время (более 30 лет) работал в Санкт-Петербургской академии наук. Это был его основной вклад в становление российской науки.
Скажем, что такое круги Эйлера и как они используются в различных областях.
Виды кругов Эйлера
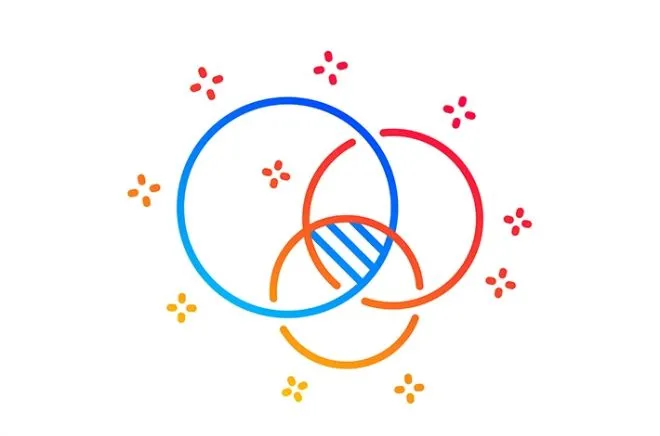
Эйлер выделил шесть типов отношений между понятиями, выраженных в соответствующей форме.
- Равнозначные. Два одинаковых круга. Например, А.С.Пушкин = автор повести «Капитанская дочка».
- Пересекающиеся. Часть одного круга частично совпадает с частью другого (человек может быть одновременно и футболистом, и поэтом).
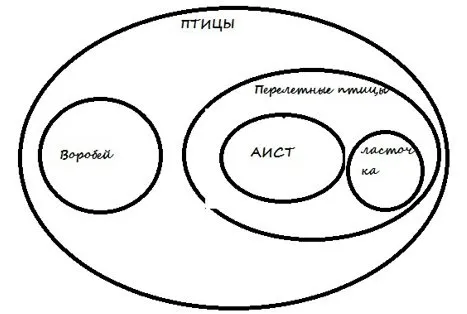
- Подчиненные. Один маленький круг внутри большого (корова относится к классу млекопитающих).
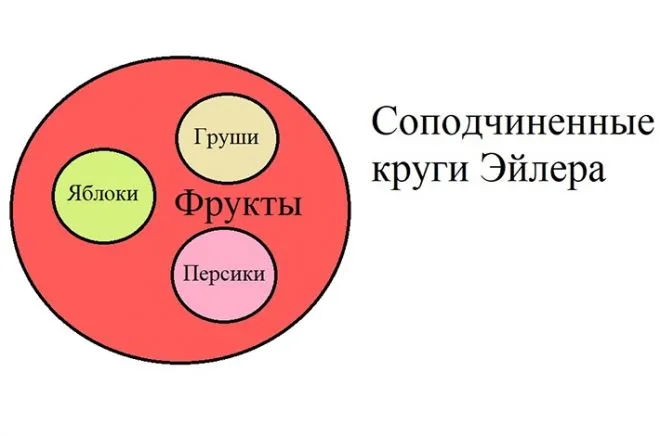
- Соподчиненные. Несколько одинаковых по размеру маленьких кругов внутри большого (яблоко, груша, персик – фрукты).
- Противоречащие. Разделенный пополам круг, каждая часть которого не имеет ничего общего с другой. Например, две конкурирующие между собой компании, производящие автомобили.
- Противоположные. Две части круга, между которыми есть свободное пространство. В отличие от предыдущей группы, между ними нет конфликта (холодное и горячее).
В сложных логических задачах могут одновременно существовать различные типы таких графиков.
Где применяются круги Эйлера
Круги Эйлера широко используются во многих упражнениях на мышление и логику. Ученые сами применяют этот метод для решения сложных математических задач. Это объясняется тем, что простая форма схемы упрощает рассуждения и позволяет визуализировать возможные решения.
Сегодня круги Эйлера широко используются в его работе: круг Эйлера — это простая форма, которую можно использовать для визуализации решения сложной математической задачи.
Основным преимуществом этого метода является его гибкость. Развитие детского мышления и сложных математических (и не только!) способностей. проблемы.
Метод схематичного представления отношений множеств — это больше, чем просто развлечение. В «Эйлеровом круге» приводятся примеры решения задач, где логика не очевидна, показывая, что этот метод можно использовать не только для решения математических задач, но и для поиска выхода из повседневных ситуаций.
Круги Эйлера и примеры задач на логику
На самом деле, круги Эйлера очень часто встречаются в нашей жизни. Уже в начальной школе ученики начинают работать со схематическими диаграммами, которые наглядно объясняют взаимосвязь между объектами и понятиями.
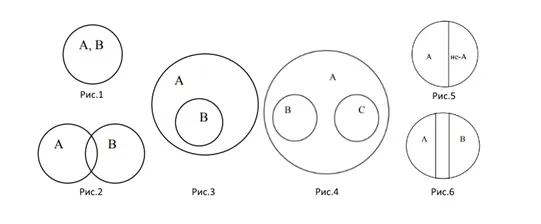
Эйлеровы круги — это геометрические структуры, используемые для упрощения распознавания рациональных отношений между объектами, понятиями и явлениями.
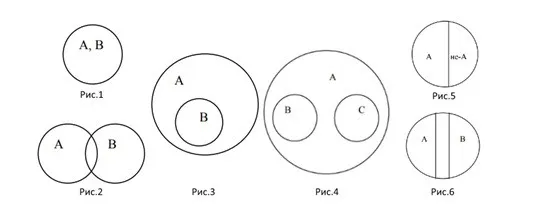
В зависимости от типа отношений между множествами, они делятся на группы.
- равнозначные (рис.1);
- пересекающиеся (рис.2);
- подчиненные (рис.3);
- соподчиненные (рис.4);
- противоречащие (рис.5);
- противоположные (рис.6).
Типичные примеры таких диаграмм:.
Самый большой зеленый набор представляет все вариации игры.
Одним из вариантов игры является производитель. Он отмечен синим овалом. Мейкер — это независимый набор и в то же время часть всей «игры».
Игры с часами также являются частью набора «Игры», но не являются частью общего набора «Создатель». Поэтому они отмечены фиолетовым овалом. Набор «курдские автомобили», с другой стороны, является независимым набором, но подмножеством набора «курдские игры».
Используя этот метод, ученые решали самые сложные математические задачи. Используя простые формы, они смогли свести любое решение к символической логике, то есть к максимальной простоте рассуждений, даже для самых сложных задач.
Затем метод был доработан Джоном Бенном в Великобритании, который ввел понятие множества наборов пересечений.
Методология очень проста в использовании — эйлеровский цикл уже преподается в детских садах для 4-5-летних детей. Однако он также достаточно прост для использования в высшей академической среде.
Применение кругов Эйлера
Основная цель использования графиков — решение составных или пересекающихся задач.
Сектора реализации: математика, логика, менеджмент, статистика, информатика и т.д. На самом деле, их гораздо больше, но перечислить их все невозможно.
Диаграмма делится на два типа.
Первый описывает соотношение понятий и их вставку друг в друга. Примеры приведены в статье выше.
Второй описывает пересечение двух различных наборов концепций с некоторыми общими чертами. Примеры включают
Примеры задач и решения
Посмотрите на проблемы, которые помогают решать эйлеровы круги в логике и математике.
Задачи для дошкольников

Первая серия: Круги Эйлера для дошкольников работают с ответами, чтобы понять, как маленькие дети знакомятся с искусством упрощения сложных математических и рациональных задач.
Задание №1 – начальный уровень.
Цель: помочь детям научиться распознавать предмет, который лучше всего подходит для двух свойств одновременно.

Правильный ответ — кубик Рубика.
Задание №2

Задание №3

Задание №4 – средний уровень.
Использование большего количества наборов усложняет задачу.

Задание №5

Задание №6
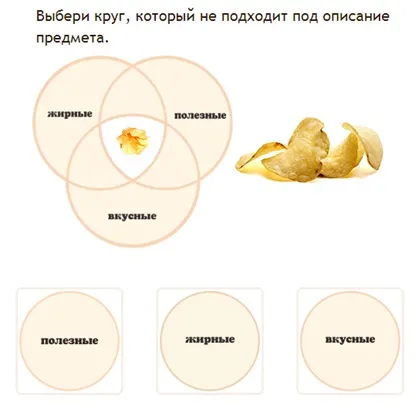
Правильное решение заключается в следующем.
Задания для школьников
Следующие логические вопросы с ответами, в которых основу решения составляют эйлеровы круги, актуальны для студентов младших курсов. Такие задания учат детей классифицировать логические перекрестки в соответствии с определенной функцией.
Задание №1
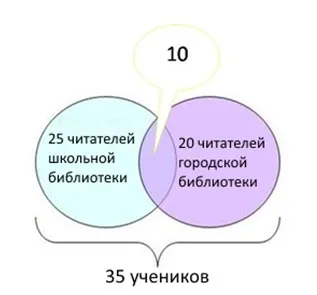
35 учеников записаны в школьную библиотеку или библиотеку начальной школы. Из них 25 регулярно посещают школьную библиотеку и 20 муниципальных библиотек.
- Посещают обе библиотеки?
- Не посещают городскую библиотеку?
- Не посещают школьную библиотеку?
- Ходят только в городскую библиотеку?
- Ходят только в школьную библиотеку?
35-20 = 15 — это левая часть синей зоны.
35-25 = 10 — правая часть фиолетовой зоны.
35-25 = 10 — также соответствующий сектор фиолетовой зоны.
35-20 = 15 — также левый синий сектор.
Задание №2 – также предназначено для младших классов, но является более сложным.
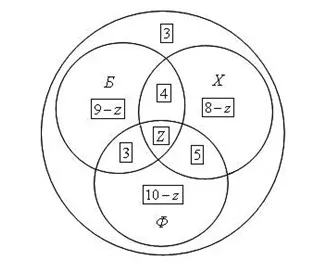
В 7-А 38 студентов. Студенты занимаются различными спортивными играми: 16 — баскетбол, 17 — хоккей, 18 — футбол. 4 студента любят баскетбол и хоккей, 3 — баскетбол и футбол, 5 — хоккей и футбол, 3 не интересуются спортом.
- Есть ли ученики, увлекающиеся всеми спортивными играми?
- Какое количество школьников интересуется только одной из спортивных игр?
Применяйте технику, реально используя форму и принимая ее за принцип, ваше мышление будет тренироваться, вы будете лучше понимать этот мир и найдете свое предназначение.
Принцип кругов Эйлера
Вспомните эмблему CHARMED. Она нужна для визуализации.

Эйлеровский мир в реальной жизни.
На самом деле все настолько просто, что лучший и самый простой из эйлеровых методов называется «три круга». Чтобы использовать эту простую технику, вам понадобятся три разных цветных карандаша и бумага. Честность, а не обман, интеллект ума! Вы научитесь мыслить еще более рационально, чем когда-либо прежде!
Помните об инструменте «Круг А». Например, «Что я хочу делать?»., «Что я делаю хорошо?»., «Как я могу получить прибыль или доход от этого?». .
Именно здесь необходима удачная серия эмблем. Нарисуйте три круга (каждый круг — другого цвета) так, чтобы круги пересекались и образовывали внутри себя клевер.
Назовите круги на носителе, дав каждому кругу свое имя. Полностью объясните важность каждого инструмента. Что вам в нем нравится? Напишите, почему вам это нравится. Напишите, сколько вы хотите выиграть, и укажите причину — поставьте цель. Напишите, почему вы делаете что-то лучше, чем другие, отдайте себе должное.
Очень важно разрабатывать круг до тех пор, пока не сформируется клевер. Да, круги могут не пересекаться. Затем вам нужно подумать о том, как их наложить друг на друга. Возможно, потребуется замена инструментов. Круги могут иметь разные размеры. Внутренние числа не обязательно должны иметь равные части. Самое главное — иметь эти детали.
Спроектировав круг и распределив работу, в центре появляется фигура, напоминающая треугольник. Эта форма является основным отношением «подмножества» и дает конечный результат. Получившаяся листовка — это путь к конечному результату.
Техника «капля в луже»
Этот метод подходит, когда вы не можете распознать объект недвижимости.

Представьте себя каплей, которая падает в воду и делает много кругов.
Идентифицируйте себя с основным кругом. Затем нарисуйте вокруг себя круги, как будто вы капаете в лужу, делая их больше. Нарисуйте не менее пяти кругов, спросите себя и отметьте их свойствами. Первый цикл определит вас, остальные помогут вам ожить.
Пройдя эти круги, вы откроете в себе качества, о которых даже не подозревали, и которые помогут вам раскрыть свой потенциал. Если вам что-то не нравится в себе, теперь вы можете проделать работу и избавиться от того, что вам не нравится. Основная цель этой техники — понять, какие качества в вас есть.
Возражаешь? Проработай!
Вы возражаете против циклов? Работайте над ними!
Ничто не покинет вас само по себе. Не позволяйте им лишить вас жизни. Предпочтительнее посмотреть на текущий образ мира по кругу, принять себя и работать с ним. Но только вы можете создать комфорт!
Если вы обнаружите, что думаете о вещах, о которых «жалеете», соберите их, пропишите и противопоставьте их работе. Во-первых, если вы ценный сотрудник, вам могут платить больше! Используйте систему Эйлера, чтобы найти рекламные инструменты и попробовать все приемы.
Плохие люди никогда не признают, что они плохие. Техника «упасть в лужу» очень подходит вам для борьбы с неуверенностью в себе и обретения отличных черт характера. У тебя они точно есть!
Эйлер не был глупым человеком. Он доказал всему миру, как легко можно решать проблемы, визуализируя их в геометрической форме. У каждого человека есть рациональный ум, и диаграммы Эйлера могут помочь вам развить его. Все равно попробуйте!
План решения включает жеребьевку для всех 54 студентов в соответствии с требованиями задачи. Известно, что клуб ВВС насчитывает 34 студента. Если добавить количество студентов-музыкантов, то их станет 32. Здесь это означает соединение ансамбля, 34 + 32 … Она состоит из студентов.
Пример решения задачи с помощью кругов Эйлера
Условия вопроса следующие. В этой таблице показано количество страниц, найденных в Интернете по определенному вопросу.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос в вопросе: сколько страниц (тысяч) выдают поисковые системы с вопросом ‘Крейсеры и линкоры’? Обратите внимание, что все вопросы выполняются практически одновременно. Поэтому все страницы со словами не изменились с момента запуска вопроса.
Для решения задачи: Используйте эйлеров круг для представления условий задачи и числа ‘1’, ‘2’ и ‘3’ для объявления полученного сечения.
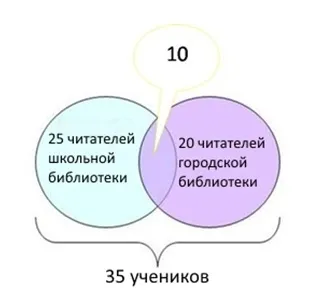
Учитывая условия задачи, составьте уравнение.
Чтобы определить количество запросов «крейсеров и военных кораблей», замените уравнение 2 в уравнении 1, чтобы получить.
4 800 + 3 = 7 000, т.е. 3 = 2 200 (7 000-4 800 = 2 200 и далее).
Затем этот результат подставляется в уравнение 3 и получается.
2 + 2 200 = 4 500, т.е. 2 = 2 300 (далее 4 500-2 200 = 2 300).
ОТВЕТ: вопрос «крейсера и линкоры» содержит 2 300 страниц.
Этот пример наглядно показывает, что сложные задачи могут быть решены очень быстро и легко с помощью круга Эйлера.
Метод Эйлера используется для упрощения задач во многих областях, от математики до управления. Он помогает находить ответы, создавая четкие логические цепочки.
Симметричная разность множеств
Симметричная разность A ∈ B — это множество, содержащее все элементы первого множества, не входящие во второе множество, и все элементы второго множества, не входящие в первое множество.
Разница между множествами записывается следующим образом.
\A \B большой треугольник над B = (A \обратный тире B)ߋ Кубок (B \обратный тире A)ߋ.
Графически разница выглядит следующим образом.
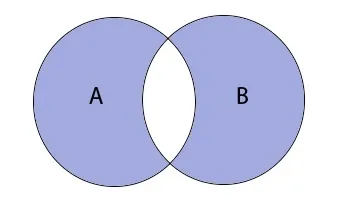
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как доказать логическое уравнение с помощью диаграммы Эйлера-Венна.
Предположим, что перед нами объединение множеств ⌘(A ⌘;\ клин ⌘;B ⌘).

Сначала рассмотрим левую часть равенства. Нарисуйте диаграмму множеств A и B. Заштрихуйте обе окружности и нанесите на график точки пересечения.

Затем заштрихуйте область за пределами набора и нарисуйте инверсию.

Обратите внимание на правую часть уравнения. Сначала нарисуйте инверсию A и изобразите область вне круга на множестве A.

Выполним ту же операцию над множеством B.
Теперь зарисуйте все пересекающиеся области черным цветом, чтобы показать обратное объединение множеств A и B.
Сравнивая области для отображения левой и правой секций, становится ясно, что они равны. Справедливость логического равенства доказывается с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Группа из 100 туристов находилась в городе N в течение трех дней. За это время 28 туристов ели в ресторане, 42 — в ресторане быстрого питания и 30 — в кафе. Десять человек посетили ресторан и ресторан быстрого питания, восемь человек посетили ресторан и кафе и пять человек посетили ресторан быстрого питания и кафе. Три человека посетили все три места. Сколько туристов ели в других местах, но так и не посетили ни одно из них?
Государство, о котором идет речь, содержит три набора P, F и K. Туристы, которые пробовали ресторан, фастфуд и кафе соответственно. Универсальное множество U — это сумма всех туристов в группе. Запишите условия задачи. где n(X) — количество элементов в множестве X.
\(n(P \; \ чашка \; F \; \ чашка \; K)}\; = \; n \; (U \; \ обратная косая черта ⌘; (P \; \ крышка \; F \; \ крышка \: K)}\)
График данных с использованием диаграммы Эйлера-Венна может помочь решить проблему. При его построении важно помнить, что в ǫ (Р \; \ кап \;°; \ кап \:К°) три элемента, а в общем ǫ (Р \; \ кап) десять элементов. \Lo_CPD2;°), три элемента уже учтены, а на пересечении множеств P и ° на диаграмме размещены семь элементов.
Теперь, когда все данные были подсчитаны один раз на графике, можно подсчитать количество туристов, посетивших хотя бы одно заведение.
Количество туристов, которые никогда не посещали ресторан, фаст-фуд или кафе, можно рассчитать следующим образом
ОТВЕТ: 20 туристов никогда не были ни в одном из этих заведений.
На олимпиаде по математике студентам предлагалось решить три задачи: одну по алгебре, одну по геометрии и одну по тригонометрии. В олимпиаде приняли участие 1 000 студентов. Результаты олимпиады были следующими: 800 участников решали задачи по алгебре, 700 — по геометрии и 600 — по тригонометрии. 600 студентов решали задачи по алгебре и геометрии; 500 — по алгебре и тригонометрии; 400 — по геометрии и тригонометрии. 300 студентов решали задачи по алгебре, геометрии и тригонометрии. Сколько студентов не решили задачу?
Начните с определения декораций и введения символики. В этом случае есть три
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используйте диаграмму Эйлера-Венна для графического представления информации, полученной в результате решения задачи.








