Квадратный корень из неотрицательного числа a — это число b, квадрат которого равен a. В этом примере числа 10 и-10 являются квадратными корнями из положительного числа 100, потому что и 10 2 = 100, и (-10) 2 = 100.
Квадратный корень: определение, примеры, свойства, график
В этой заметке мы рассмотрим, что такое квадратный корень, приведем примеры, перечислим его основные свойства и покажем, как выглядит график его функции.
Арифметическим квадратным корнем из a является число x, которое при возведении во вторую степень дает a.
Квадратный корень (иногда называемый корнем второй степени) обозначается специальным символом — √. Например, √4 означает «квадратный корень из четырех». .
Другой вид обозначения — 2. Однако число 2 обычно опускается и используется таким образом.
Подвыражение для приведенного выше примера равно 4. Однако оно может быть представлено не только числом, но и математическим выражением, содержащим как буквы, так и цифры. Например: .
Вычисление значения x называется извлечением квадратного корня из числа a (что является обратным действием возведения в квадрат):
Квадратный корень можно извлечь только из положительного числа. Кроме того, ответ ( x ) всегда будет больше нуля.
Примечание:
Для простоты можно выучить или всегда иметь под рукой таблицу квадратных чисел, хотя бы до 10-20.
График квадратного корня
В координатной плоскости функция имеет следующий вид:
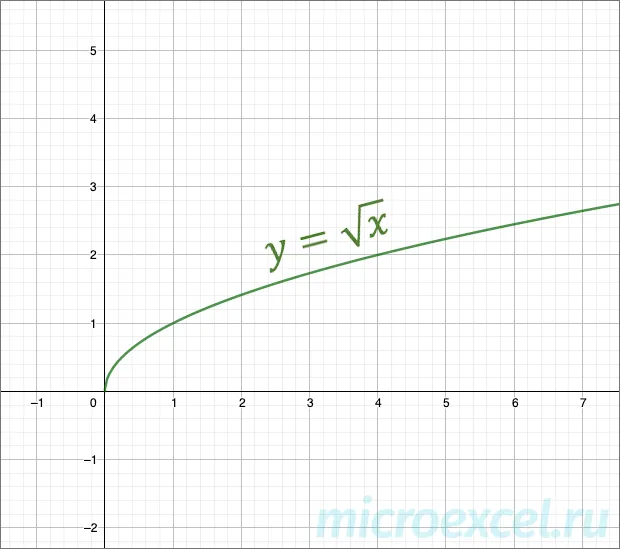
График начинается в точке, монотонно возрастает и находится исключительно в первой четверти координатной плоскости, так как он определен только для, в которой он принимает положительные значения y.
Публикации по теме:
- Показатель степени: определение и свойства
- Таблица логарифмов
- Определение логарифма, его свойства и график
- Натуральный логарифм числа
- Теорема Виета: для квадратного/кубического уравнения, обратная
- Степени натуральных чисел
- Факториалы натуральных чисел
- Арифметическая прогрессия: определение, формулы, свойства
- Геометрическая прогрессия: определение, формулы, свойства
- Нахождение производной степенной функции
- Десятичный логарифм числа
- Основное логарифмическое тождество
- Логарифм произведения (сумма логарифмов)
- Логарифм деления (частного) или разность логарифмов
- Решение логарифмических неравенств
- Квадрат суммы: формула и примеры
- Квадрат разности: формула и примеры
- Разность квадратов: формула и примеры
- Куб суммы: формула и примеры
- Великая теорема Ферма
- Малая теорема Ферма
- Правильные, неправильные и смешанные дроби
- Правила сравнения обыкновенных дробей
- Приведение дробей к общему знаменателю
- Нахождение наименьшего общего кратного
- Нахождение наибольшего общего делителя
- Вычитание обыкновенных дробей
- Умножение обыкновенных дробей
- Деление обыкновенных дробей
- Деление числа на обыкновенную дробь
- Нахождение дроби от числа и наоборот
- Умножение десятичных дробей: правила, примеры
- Деление десятичных дробей: правила, примеры
- Деление десятичной дроби на обыкновенную и наоборот
- Деление натурального числа на десятичную дробь
- Умножение обыкновенной дроби на десятичную: правило, примеры
- Округление десятичных дробей: правила, примеры
- Бесконечные периодические десятичные дроби
- Что такое модуль действительного числа
- Основные свойства модуля действительного числа
- Сравнение модулей действительных чисел
- Что такое среднее арифметическое чисел: двух, трех, четырех и тд
- Признаки делимости чисел
- Правила раскрытия скобок с примерами
- Что такое арифметическое равенство
- Тождество и тождественные выражения
- Именные названия степеней тысячи
- Экспонента: определение, формула, свойства, график
- Показательная функция: определение, формула, свойства, график
- Степенная функция: определение, формула, виды графиков
Применение операции корня к числам
Квадратный корень из, т.е. решение уравнения. 1 2
Рациональные числа
Квадратный корень из рационального числа и
Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: » width=»» height=»» />где 3 4 .
Действительные числа
В случае с натуральными числами она не всегда разрешима в рациональных числах, что привело к появлению новых числовых полей. Самым старым из этих расширений является поле вещественных (действительных) чисел.
Теорема Для каждого положительного числа a существует ровно два вещественных корня, равных по модулю и противоположных по знаку. 5
Неотрицательный квадратный корень из положительного числа является числовым квадратным корнем и обозначается символом радикала
Комплексные числа
В области комплексных чисел всегда есть два решения, которые отличаются только знаком (за исключением квадратного корня из нуля). Квадратный корень из комплексного числа равен, но использовать эту нотацию следует с осторожностью. Распространенная ошибка:
=\sqrt=1 » width=»» height=»» />
Для получения квадратного корня из комплексного числа удобно использовать экспоненциальную форму представления комплексного числа: если
,
» width=»» height=»» />,
где модуль корня понимается в терминах числового значения, а k может принимать значения k=0 и k=1, так что ответ в конечном итоге дает два разных результата.
Квадратный корень как элементарная функция
Вещественный анализ

График функции
Квадратный корень также является функцией вещественной переменной, которая соответствует числовому значению корня. 7 Эта функция является частным случаем функции мощности. Это гладкая функция в.
Комплексный анализ
Квадратный корень в элементарной геометрии
Квадратные корни тесно связаны с элементарной геометрией: дан отрезок длиной 1, используйте компас и линейку для построения тех отрезков, длина которых задана целыми числами, точками четырех арифметических действий, квадратными корнями и ничем другим. 11
Во многих языках программирования на уровне функций (а также в языках разметки, таких как sqrt, от английского square root «квадратный корень».
Квадратные корни. Арифметический квадратный корень

В этом уроке мы разберемся, что такое квадратный корень. Мы введем понятие арифметического квадратного корня. И мы научимся новому действию под названием извлечение квадратного корня.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный кабинет.

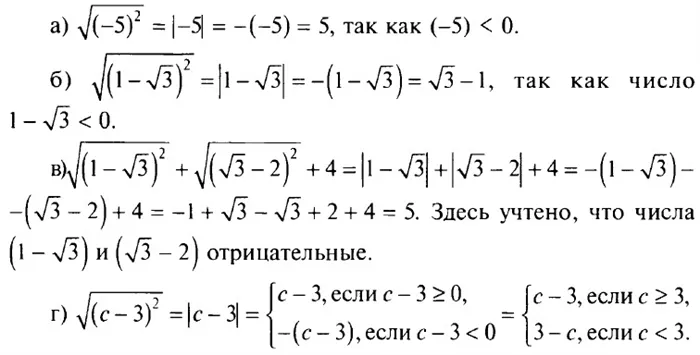
2. Распространите видеоуроки в своих личных кабинетах среди учеников.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Квадратные корни. Арифметический квадратный корень»
На этом уроке мы рассмотрим такие новые понятия, как квадратные корни и арифметические квадратные корни. Мы также научимся находить значения корней.
Проблема: Мама подарила Маше квадратный участок земли для клумбы. Площадь участка равна 100 м 2. Определите длину стороны участка.

Числа 10 и минус 10 называются квадратными корнями уравнения
Определение
Квадратный корень из a — это число, квадрат которого равен a.
Давайте вернемся к проблеме. Мы знаем, что длина — это положительная величина. Поэтому квадратный корень из второго уравнения, минус 10, не подходит. И тогда длина стороны партера Маши равна 10 метрам.
При решении этой проблемы мы столкнулись с двусмысленностью: У нас есть два корня, но только один подходит к проблеме. А чтобы избежать проблем при выборе корня, мы вводим понятиеАрифметикаКвадратный корень.
Определение:
Арифметический квадратный корень из a равеннеотрицательное значениеквадрат которого равен a.
Обратите внимание, что в определении фраза «неотрицательное число«. Почему ты не можешь просто сказать.» положительное число «?? …потому что квадрат нуля — это само число ноль. А это, как вы знаете, не является ни позитивным, ни негативным. По этой причине мы используем термин «неотрицательное число».
Арифметический квадратный корень из числа a называется следующим образом:
Символ радикала (от латинского слова «radix» — корень).
Выражение, расположенное ниже корня, называется подкорнем.
При чтении нотации слово «арифметический» не произносится, а просто читается как «квадратный корень из а».
Нахождение арифметического квадратного корня из числа называется извлечением квадратного корня.
Рассмотрим несколько примеров извлечения квадратного корня из числа. Поэтому мы хотим найти значения квадратного корня.

Помните, что извлечь квадратный корень можно только из неотрицательных чисел.
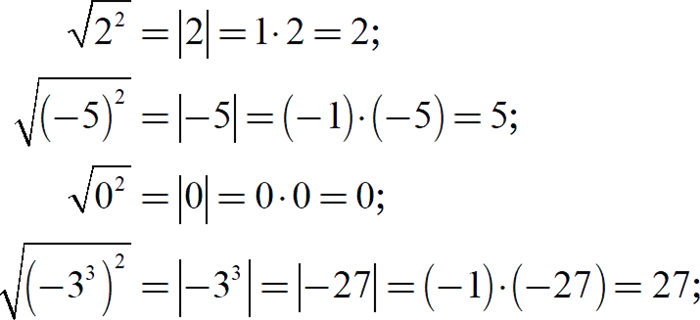
Не имеет смысла делать это с неотрицательным числом. Поскольку не существует числа, квадрат которогоотрицательныйНомер.
Из определения арифметического квадратного корня следует, что для любого a, в котором выражение .
Задача 1: Найдите число, арифметический квадратный корень которого равен: 1? 4; 0,3.
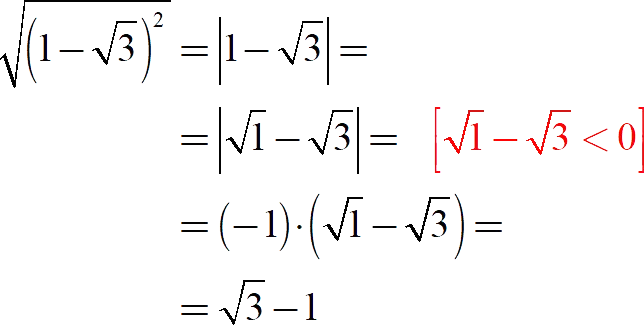
Задание 2: Найдите значение выражения.
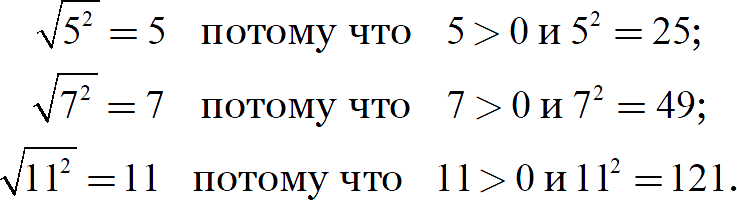
Квадратный корень из α — это число, квадрат которого равен α.
Квадратный корень
Для некоторых сил, которые используются чаще других, в математике существуют специальные названия, которые изначально пришли из геометрии. Это вторая и третья силы.
Вторая сила — это длина стороны квадрата, когда нужно вычислить его площадь. Если вы хотите определить объем куба, увеличьте длину его граней на третью степень. Поэтому вторая сила называется квадратом числа, а третья — кубом.
Следовательно, корень второй степени называется квадратом, а корень третьей степени — кубом. Квадратный корень — единственный корень, который не содержит экспоненту при записи над корнем:
Арифметический квадратный корень из данного числа — это положительное число, которое нужно возвести во вторую степень, чтобы получить данное число.
- Как вычислить квадратный корень
- Как находить квадратный корень
- Как вычислить квадратный корень числа
- Как извлечь квадратный корень
- Как вычислить корень
- Как вносить под знак корня
- Как извлечь корень
- Как написать корень квадратный
- Кто открыл квадратные корни
- Как определить корень
- Как ввести квадратный корень
- Как решать корни
- Как умножить корень на число
- Как внести число под корень
- Как возвести корень в квадрат
- Как найти корень квадрата
- Как найти квадратный корень из степени
- Как вычислить корень четвертой степени
- Как сложить корень и число
- Как перемножить корни
- Как возвести в корень число
- Как вычислить корень пятой степени
- Как вычитать квадратный корень
- Как внести множитель под корень