Поэтому легко понять, что стек хранит небольшие данные, к которым можно получить доступ как можно быстрее, а куча хранит сложные блоки с большим объемом данных.
Понятие и виды алгебраических выражений
В математическом языке мы используем специальные «слова», называемые математическими выражениями, а математические символы служат «буквами».
Десятичная система счисления с арабскими цифрами 0,1,2…9
Латинский a,b,…,z,A,B,…,Z Греческий a,b,…,ω,L,S,Ω Русский НОД, НОК,$ V_, S_ $
Числовые операции: +,-,*,/ Другие операции: 3500^3,, \Стрелка вправо, \&, ,<\int>, $
Символы сравнения: $ \lt, \gt, \le, \ge,
eq $ Другие символы: $\forall, \exists, \to, \bot$
Список математических символов становится все длиннее и длиннее. Наконец, каждый имеет право изобрести свой собственный иероглифический символ, объяснить его значение определением и предложить правила его использования при написании своих работ. Если символ окажется успешным и востребованным, то со временем он появится в других произведениях и проложит свой самостоятельный путь по миру.
Математическое выражение — это конечная смысловая комбинация математических символов, построенная по определенным правилам.
Предположим, что по правилам мы строим математические выражения, состоящие из различных чисел (образованных из цифр, дроби и десятичной точки), знаков для арифметических операций, возведения в соответствующую меру, корней и скобок:
Например: $(1+5^2):3\frac 14, \frac, \frac 12 — \frac 13 \cdot (-\sqrt 9) $.
Такие выражения называются числовыми терминами.
Например: $(1+5^2):3\frac 14 \gt 7, \frac \lt 0, \frac 12 — \frac 13 \cdot (-\sqrt 9) = 1\frac 12$.
Такие выражения называются арифметическими формулами.
п.2. Определение и понятие переменной
Формула имеет дополнительное значение по сравнению с термином: она может быть «истинной» или «ложной». Три приведенные выше формулы верны. Но 2+2=5 — это ложная числовая формула.
На практике очень часто бывает так, что в расчетах изменяется только одна величина, а остальные остаются постоянными. Например, нам нужно рассчитать площадь панелей с разной длиной 7 м, 10 м и 15 м, но одинаковой шириной 4 м. Тогда $S_1 = 4 \cdot 7 = 28 м^2, S_2 = 4 \cdot 10 = 40 м^2, S_3 = 4 \cdot 15 = 60 м^2 $. Эти расчеты можно обобщить, записав S=4a, где первый множитель — фиксированная ширина 4 м, а второй — переменная длина а м. Такое обобщение называется «переменной вставкой»; оно удобно тем, что дает универсальную формулу для расчетов.
Переменная — это литеральный символ в математическом выражении, который может принимать различные значения.
Математические выражения с переменными также могут быть терминами или формулами.
Формулы с переменными: $(1+a^2):3 \frac 14 — b>Переменные члены: $(1+a^2):3 \frac 14 — b, \frac, \frac 12 — \frac \cdot (-\sqrt 9) $<0, \frac 12 - \frac \cdot (-\sqrt 9) = f-3 $
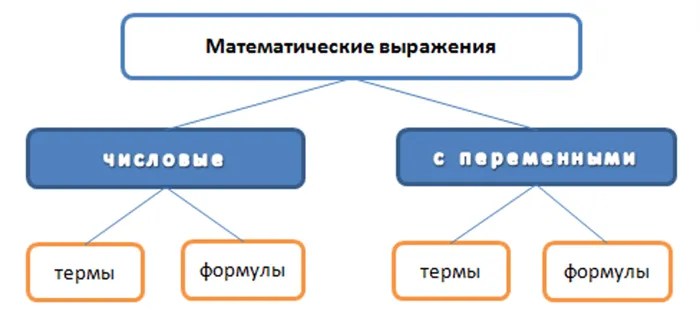
п.3. Алгебраические и трансцендентные выражения
b, \frac
Математические выражения делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраические выражения — это математические выражения, состоящие из различных чисел и переменных, символов арифметических операций, рациональных экспонент, корней, скобок и знаков соотношения.
Если алгебраическое выражение не предполагает деления на переменные и извлечения корней из переменных (или приведения к степени с дробным показателем), оно называется интегральным выражением.
$7, \frac +48, (\sqrt 7b-4c^3)^5$ — термы $b-\frac 32 = 8,28c^2>Примеры интегральных выражений:
\sqrt 2$ — формулы
Когда алгебраическое выражение содержит деление на переменные в дополнение к характеристикам целочисленного выражения, оно называется дробным выражением.
$\frac 7m, 3a^2 + \frac, (\sqrt 7b-\frac )^5$ — термы $b-\frac = 8,28c^2>Примеры дробных выражений:
\frac$ — формулы
Целочисленные и дробные выражения объединены в категорию логических выражений.
Если алгебраическое выражение содержит извлечение корня из переменных (или экспоненцию переменных с дробной экспонентой), оно называется иррациональным выражением.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Примеры иррациональных выражений:

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный кабинет.
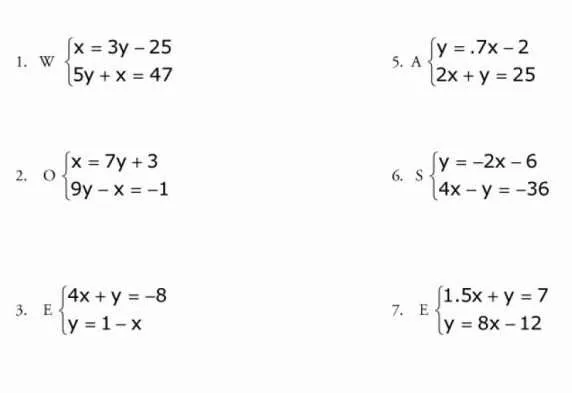
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Выражения с переменными»
2. Распространите видеоуроки в своих личных кабинетах среди учеников.
— Ввести понятие «выражение с переменными»,
— Ввести понятие «область определения выражения».
Помните, что в прошлом уроке мы говорили об арифметических выражениях и значениях арифметических выражений.
Арифметическое выражение — это набор данных, состоящий из чисел, символов для арифметических операций и скобок для указания порядка операций.
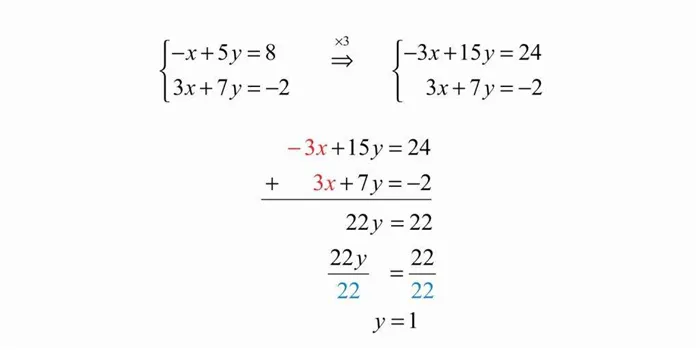
Значение арифметического выражения — это число, полученное при выполнении всех операций арифметического выражения.
Определение.
Буквенное выражение — это обозначение, состоящее из цифр, букв, числовых символов и круглых скобок, указывающих порядок выполнения операций.
Строчные буквы латинского алфавита чаще всего используются для написания буквенных выражений.
Вы также должны знать, что письмо — это выражение.
Давайте решим эту проблему.
Велосипедист движется со скоростью 15 км в час. Какое расстояние пройдено за время t?
Известно, что расстояние можно найти, умножив скорость на время. Тогда расстояние, пройденное велосипедистом, равно 15t.
Теперь, например, если мы хотим найти расстояние, пройденное велосипедистом за 3 часа, мы заменяем t на 15 ∙ t на число 3, то есть находим значение выражения при t = 3 и получаем 45 км.

В нашем случае буква t называется переменной, а само выражение — выражением с переменной.
То есть, переменная — это буква, содержащаяся в буквенном выражении, которая может принимать различные значения.

Если заменить переменную выражения числом, то получится числовое выражение.
Прежде чем перейти к решению задач, вернемся к выражению 15t, которое мы получили при решении первой задачи. В этом случае переменная t может принимать только положительные значения, поскольку время не может быть отрицательным, и этот набор значений называется областью применения выражения 15t.
Поэтому важно помнить, что область видимости выражения может включать только те значения переменных, которые приводят к числовому равенству, имеющему смысл.


Теперь давайте выполним несколько упражнений.
Последнее упражнение.

История вклада переменных начинается в семнадцатом веке с ученого Рене Декарта.
Известные величины он обозначал начальными буквами алфавита: a, b и т.д., а для неизвестных предлагал использовать последние буквы: x, y, z. Стоит отметить, что Декарт считал такие переменные неотрицательными числами, и когда ему встречались отрицательные параметры, он ставил перед переменной знак минус или, если знак числа был неизвестен, дефис. Но со временем имена переменных стали обозначать числа с произвольными знаками, и начало этому положил математик Йоханнес Худде.
С переменными легче решать вычисления в математике, например, как сегодня решаются диагональные уравнения? Мы вводим переменную. Например:
Вы принимаете k за x2, и уравнение выглядит просто:
Неравенства, примеры решения
В этом заключается преимущество введения переменных в математике.
Неравенство — это обозначение, в котором два математических выражения или два числа соединены символами сравнения:, ≤, ≥. Они могут быть строгими и обозначаться символами или нестрогими ≤, ≥.
Они могут быть как строгими, так и нестрогими, обозначаться знаками или символами или без них: Французские местоимения: типы и формы
Эти знаки были впервые введены Томасом Гэрриотом. После смерти Томаса была опубликована его книга с этими символами, они приглянулись математикам, и со временем стали повсеместно использоваться в математических расчетах.
При решении неравенств с одной переменной необходимо следовать некоторым правилам:
Решить неравенство — значит найти все допустимые значения переменной.
Пример с одной переменной:
Решите уравнение как обычное линейное уравнение — переместите члены с переменной влево, члены без переменной вправо и добавьте аналогичные члены:
Разделите обе части неравенства на 10 и получите:

В примере решения неравенства с одной переменной для наглядности проведем числовую линию и отметим точкой 20, так как неравенство строгое и это число не входит в набор решений.
Решением этого неравенства является (20; +∞).
Решение нестрогого неравенства — это то же самое, что и решение строгого неравенства:
Квадратные неравенства
Но есть и исключение. Форма x ≥ 5 обозначается так: x больше или равно пяти, поэтому число пять входит в множество всех решений неравенства; то есть, записывая ответ, мы ставим скобку перед числом пять.
Если взять квадратное уравнение вида ax2 + bx +c = 0 и поменять знак с равно на знак неравенства, то получится квадратное неравенство.
Чтобы решить квадратное неравенство, нужно знать, как решить квадратное уравнение.
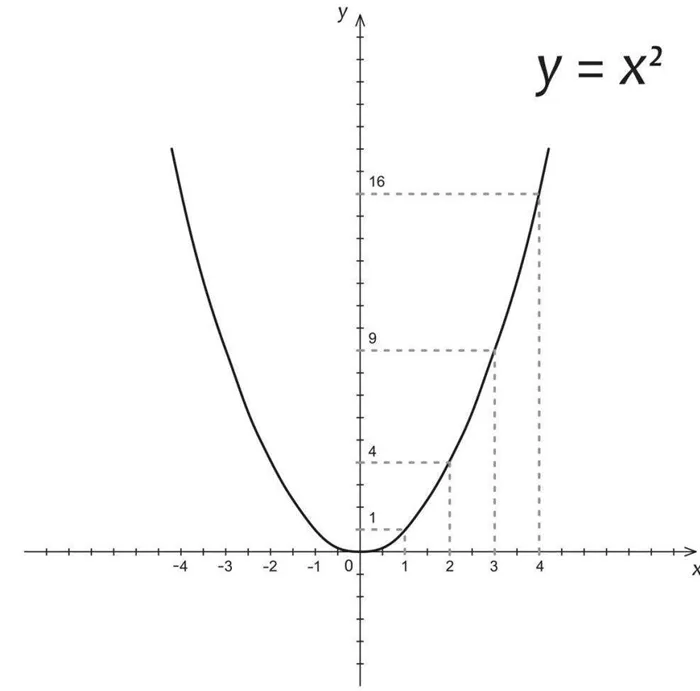
y = ax2 + bx + c — квадратичная функция. Мы можем решить ее с помощью дискриминанта или теоремы Виета. Вспомните, как решаются подобные уравнения:
1) y = x2 + 12x + 11 — функция является параболой. Ветви направлены вверх, так как знак коэффициента «a» положительный.
2) x2 + 12x + 11 = 0 — Приравняйте к нулю и решите с помощью дискриминанта.
D = b2 — 4ac= 144 — 44 = 100>a = 1, b = 12, c = 11
0, 2 корня
Использование формулы для корней квадратного уравнения дает следующее:
Вы также можете решить это уравнение с помощью теоремы Виета:
x1 + x2 = -b/a, x1 + x2 = -12
x1x2 = c/a, x1x2 = 11
Компьютерная грамотность с Надеждой

Используя метод подгонки, мы получаем одинаковые корни уравнения.
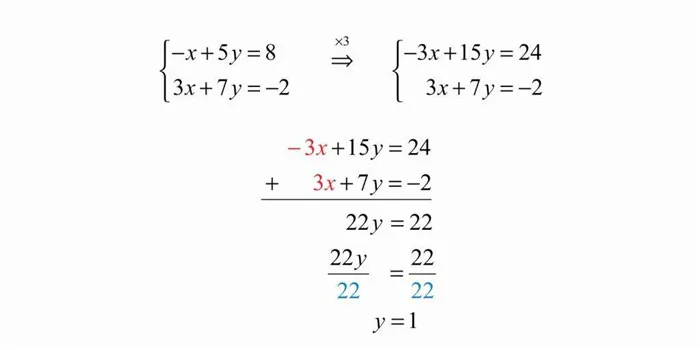
Прежде чем перейти к вопросу о том, что такое переменная в программировании, давайте попробуем понять, зачем нужны и константы, и переменные. Алгебра существенно отличается от арифметики тем, что имеет дело только с числами, тогда как алгебра вводит понятие переменных.
Согласитесь, что 2 + 3 = 5 — это нечто совершенно иное, чем выражение: a + b = c.
В чем разница? Не только потому, что в алгебре вместо цифр используются буквы латинского алфавита, но и на уровне вычитания.
Числовые выражения, что бы вы с ними ни делали, в конечном итоге дают только числовые результаты.
Но абстрактные буквенные выражения становятся формулами, законами и следствиями, а если выйти за рамки алгебры, то леммами и теоремами и в целом ведут к дифференциальному и интегральному исчислению, математическому анализу и так далее. Правда, латинских букв не хватает (в математическом анализе), но используются греческие буквы, всякие «дельта», «сигма» и тому подобное. Но это связано не столько с отсутствием букв, сколько с постоянным увеличением степени абстракции, которая (абстракция) требует новых средств выражения.
Почему? Потому что определенный, пусть и невысокий, дополнительный уровень абстракции позволяет мыслить иначе, действовать иначе, учиться иначе и достигать иных результатов, чем при более низком уровне абстракции.
Калькуляторы дружат с константами
То же самое относится и к компьютерной грамотности. Сначала мы можем говорить о самом низком уровне абстракции, например, об арифметике в программировании.
- Вводим на калькуляторе первое число, например, «2»,
- нажимаем на знак «плюс»,
- вводим второе число, скажем, «3» (см. рис. 1),
- и затем нажимаем знак «=».
Возьмем, к примеру, калькулятор. Что он может сделать? Довольно много: он может выполнять ряд арифметических и даже более сложных операций.
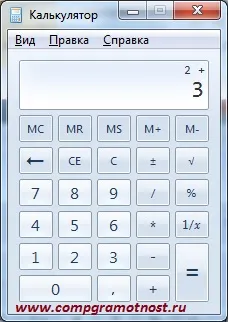
И что мы получаем? Очевидно, что значение «5». Арифметика. Но с помощью компьютерной технологии — калькулятора.
Рисунок 1. Сложение констант 2+3 на карманном калькуляторе (Windows 7).
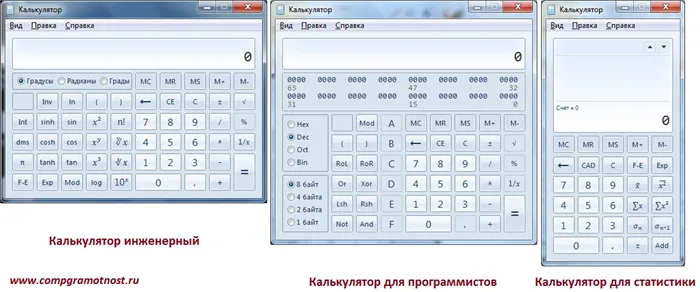
Мы не будем подробно останавливаться на возможностях карманных калькуляторов. Например, можно подумать о более продвинутых калькуляторах: для инженеров, для программистов, для обработки статистических данных и т.д. (см. рис. 2).
Рисунок 2. Некоторые типы калькуляторов, доступные в Windows 7.
Программы дружат с переменными величинами
Но продвинутые калькуляторы все равно останутся калькуляторами, то есть будут выполнять вычислительные операции различной сложности. Это потому, что это уровень абстракции, самый низкий, на уровне чисел. Калькуляторы не могут обрабатывать ничего, кроме числовых выражений.
И если бы следующий, новый уровень абстракции не вошел в компьютерную науку, программирование в том виде, в котором оно существует сегодня, не появилось бы. Программирование, позволяющее создавать программное обеспечение для всех слоев общества, с удобным интерфейсом, т.е. интерфейсом, который легко использовать в дальнейшем.
Как это работает? Давайте объясним с некоторыми упрощениями, чтобы не углубляться в сложную область программирования.
Во-первых, обратите внимание, что в программировании все выражения записываются наоборот, чем в алгебре. Если в алгебре вы сначала указываете операторы (переменные), с которыми хотите работать, а затем, после знака равенства, указываете результат, как в примере
В программировании все наоборот: сначала дается результат, а затем действие, т.е:
Не случайно я пишу строчными (заглавными) буквами, а не прописными (маленькими):
во-первых, чтобы отличить алгебру от программирования, и
Во-вторых, потому что изначально в программировании в нашей стране использовались в основном заглавные буквы латинского алфавита.
Вместо латинских заглавных букв мы заменили кириллицу строчными буквами, потому что где еще вы найдете коды для русских букв! Это связано с тем, что многие переводчики языков программирования в нашей стране только копировали западные аналоги, а не разрабатывали их с нуля. И там, где все это копировалось, русского языка по понятным причинам не было. Правда, там были примеры наших «родных» языков программирования.
И я пишу компьютерные выражения не в середине строки, как это принято в алгебре, а в начале строки, как это принято в программировании. Это вопрос синтаксиса языков программирования, правил написания выражений на этих языках. В алгебре существуют одни правила, а в программировании — другие, хотя буквы могут быть одинаковыми в обоих случаях.
Почему в программировании теперь пишут C = A + B в обратном порядке? Трудно сказать. Оказалось, что сначала нужно написать результат, а потом действие.
Что дает нам это «волшебное» выражение с буквами вместо цифр для программирования? Выяснилось, в чем разница между константами и переменными:
5 = 2 + 3 (записано в обратном порядке только для сравнения) и
Давайте разберемся. Что может получиться в результате сложения 2+3? Большинство людей, конечно же, ответят «5». И хотя это почти правильный ответ, я думаю, мы с вами согласимся.
Почему почти? Потому что это правильный ответ для десятичной системы. Для квадратичной системы, в которой используются только цифры от 0 до 3, ответ будет «11», да, да, одиннадцать, вы можете быть уверены в этом. А в пентатонической системе, где добавляется цифра 4, ответ будет «10».
Независимо от того, какая это система счисления, результат 2+3 всегда одно и то же число (константа). В десятичной системе (к которой я давно вернулся) это «5» и только «пять».
Но что такое A + B? Ответ очевиден: все зависит от того, чему равны A и B. Поэтому результат 2+3 всегда будет равен 5, а результат A+B будет разным в зависимости от того, каковы A и B.
Неравенства, примеры решения
Они могут быть как строгими, так и нестрогими, обозначаться знаками или символами или без них: Французские местоимения: типы и формы
Эти персонажи были впервые представлены Томасом Гэрриотом. После смерти Томаса появилась его книга с этими обозначениями, они понравились математикам, и со временем стали повсеместно использоваться в математических расчетах.
Эти знаки были впервые введены Томасом Гэрриотом. После смерти Томаса была опубликована его книга с этими символами, они приглянулись математикам, и со временем стали повсеместно использоваться в математических расчетах.
Решить неравенство — значит найти все допустимые значения переменной.
Решите уравнение как обычное линейное уравнение — переместите члены с переменной влево, члены без переменной вправо и добавьте аналогичные члены:
Разделите обе части неравенства на 10 и получите:

В примере решения неравенства с одной переменной для наглядности проведем числовую линию и отметим точкой 20, так как неравенство строгое и это число не входит в набор решений.
Решением этого неравенства является (20; +∞).
Решение нестрогого неравенства — это то же самое, что и решение строгого неравенства:
Квадратные неравенства
Но есть и исключение. Форма x ≥ 5 обозначается так: x больше или равно пяти, поэтому число пять входит в множество всех решений неравенства; то есть, записывая ответ, мы ставим скобку перед числом пять.
Если взять квадратное уравнение вида ax2 + bx +c = 0 и поменять знак с равно на знак неравенства, то получится квадратное неравенство.
0, 2 корня
Использование формулы для корней квадратного уравнения дает следующее:
x1x2 = c/a, x1x2 = 11
Парабола

Используя метод подгонки, мы получаем одинаковые корни уравнения.
1 Определите, куда направлены ножки параболы.
2 Приравняйте функцию к нулю и найдите корни уравнения.
3. построить прямую линию, положив корни на эту линию, и построить параболу, чтобы найти необходимый интервал, который зависит от знака неравенства.
Запишите его в виде функции:
Установите его равным нулю.








