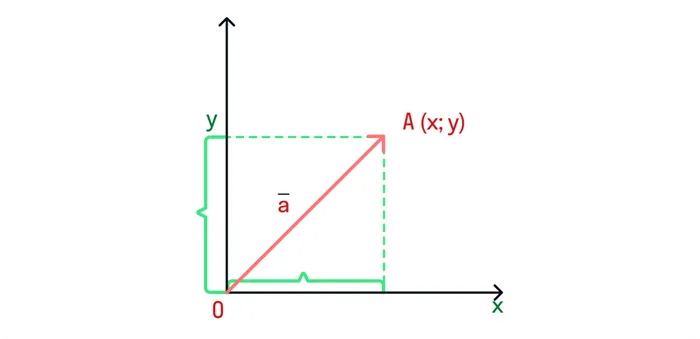
Каждый вектор имеет свою длину, которая равна расстоянию между его началом и концом. То есть, если его начало находится в точке A, а конец — в точке B, то длина вектора равна длине отрезка AB. Обозначьте длину вертикальными скобками:
Операции с векторами
Мы постепенно показываем вам математику, которая выходит за рамки школьной программы. Мы начали с введения в векторы, теперь давайте сделаем следующий шаг.
Давайте еще раз вспомним основные идеи:
- Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
- В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
- Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
- Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.
С векторами можно выполнять определенные математические операции. Давайте поговорим о них.
Правильно — векторы
Математики часто говорят «векторы» во множественном числе, но словарь правильно говорит «векторы». Это технические термины, такие как «контракты», «бухгалтеры» и «серверы». Мы используем «векторы», но если вы находитесь в баре с математикой почтовых индексов, лучше сказать «векторы».
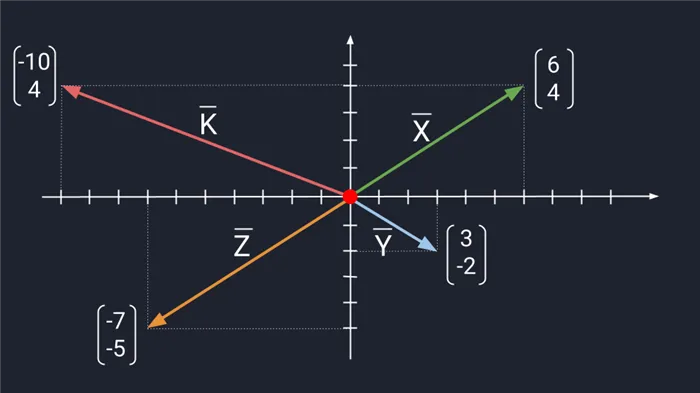
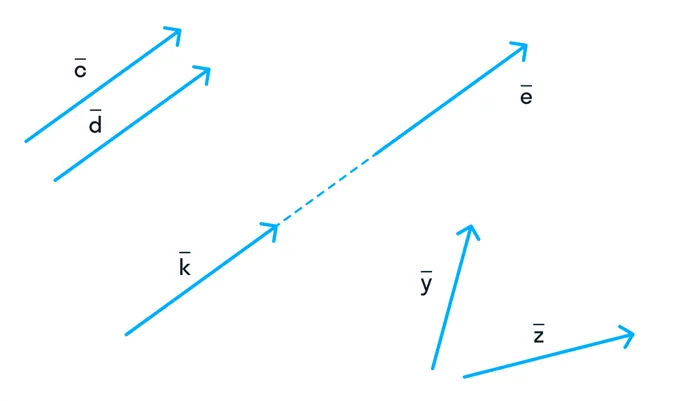
Давайте представим четыре вектора, которые находятся в двумерном пространстве и пока не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.
Поскольку векторы находятся в одном и том же пространстве, координаты каждого вектора состоят из одинакового количества чисел. У нас есть пример с двумерным пространством и двумя числами. Это будет выглядеть следующим образом: X = (6, 4); Y = (3, -2); Z = (-7, -5); K = (-10, 4).
Если у нас есть несколько векторов с одинаковым количеством чисел, мы можем складывать эти числа элемент за элементом. Для этого мы берем первое число одного вектора и прибавляем его к первому числу другого вектора, и так далее.
Предположим, мы хотим сложить векторы X и Y.
X = (6, 4) Y = (3, -2) X + Y = (9, 2)
Кажется, все просто: добавьте все координаты по одной и добавьте результаты к исходным изображениям. Вы можете сделать это с любым количеством координат. Помните, что вектор — это не обязательно стрелка в двумерном пространстве. Она может находиться и в десятимерном пространстве — с математической точки зрения это не имеет значения.
Примером может служить сложение векторов с пятью координатами:
X = (6, 4, 11, 14, 99) Y = (3, -2, 10, -10, 1) X + Y = (9, 2, 21, 4, 100).
Интуитивное изображение сложения
Для интуитивного восприятия удобно использовать векторы с двумя координатами. Удобно рисовать их в координатной плоскости и изучать геометрию таким образом.
Например, можно показать на плоскости, как происходит сложение двух векторов. Для этого существует два метода: метод треугольника и метод параллелограмма.
Метод треугольника: Положите векторы X и Y на прямую линию между ними. Для этого мы берем вектор X, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается с конца вектора X и заканчивается стрелкой вектора Y. Этот вектор является результатом сложения. Представьте, что он является дочерним по отношению к двум векторам.
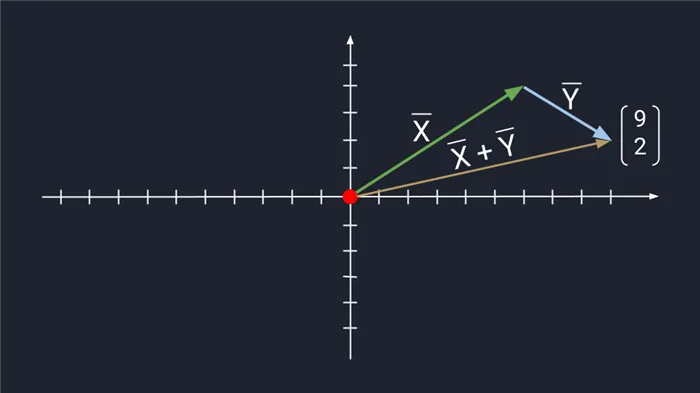
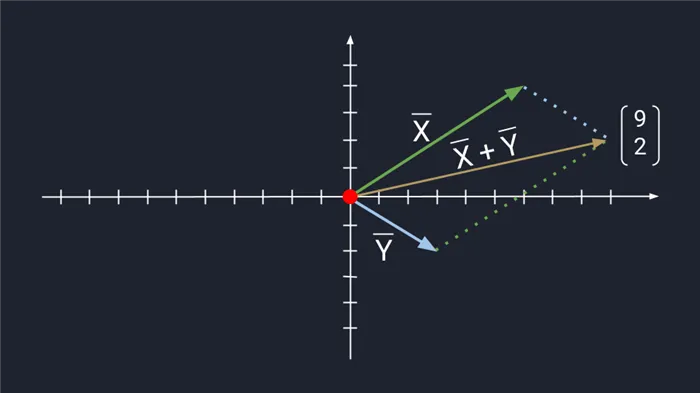
Чтобы использовать метод параллелограмма, векторы X и Y должны иметь одну и ту же начальную точку. Затем мы удваиваем векторы X и Y, формируем параллелограмм и получаем новый вектор. В новом векторе мы соединяем начальную точку с начальной точкой удвоенных векторов — стрелка проходит через середину параллелограмма. Длина нового вектора равна сумме векторов X и Y.
Сложение по методу параллелограмма и треугольника дает тот же результат. Поэтому выбирайте тот вариант, который лучше всего подходит для решения проблемы.
Геометрическая и алгебраическая интерпретация умножения
Геометрическая интерпретация: Произведение ненулевого вектора на число — это вектор, который приклеен к данному вектору, то есть лежит в направлении данного вектора, если число больше нуля, или в противоположном направлении, если число отрицательное, и его нормаль равна единице данного вектора, умноженной на модуль числа.
Алгебраическая интерпретация: Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам вектора, умноженного на число.
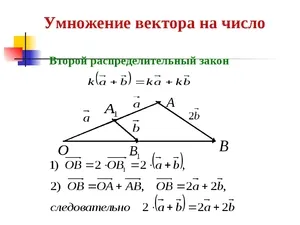
Типичным примером умножения вектора на число является второй закон Ньютона, который часто применяется для решения задач в физике. Умножение обеих частей закона Ньютона на массу тела дает следующую формулу:
Эта формула записана в векторной форме:
В данном случае речь идет не просто о модулях, т.е. длинах векторов. С помощью векторной формы можно определить направление вектора. Согласно ранее рассмотренному определению для произведения вектора и числа, результат такой операции не влияет на направление вектора. Его нельзя повернуть на любой угол путем умножения на число. Результат произведения отличается только длиной вектора. Таким образом, векторы \(\vec\) и \(\vec\) имеют одинаковое направление, но разную длину. В этом случае длина векторов отличается на коэффициент m.
Понятие, основные свойства
Если вектор \(\vec\) равен произведению ненулевого числа k и ненулевого вектора \(\vec\), т.е. \(\vec=k*\vec\), то верно следующее утверждение:
Вектор может быть умножен на число как скалярная величина. Результатом также будет вектор. После умножения длина данного вектора изменяется:
- длина вектора будет увеличена при умножении на число, модуль которого больше 1;
- длина вектора уменьшится в том случае, когда модуль числа меньше 1.
Если вектор умножить на положительное число, то полученный вектор будет иметь то же направление, что и исходный вектор. Если вектор предполагается умножить на отрицательное число, то результирующий вектор идет в противоположном направлении.
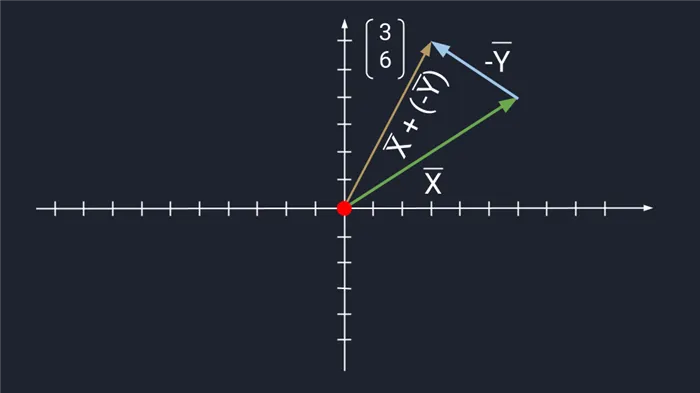
Когда вектор создается из числа, его нельзя повернуть на любой угол относительно исходной позиции. Таким образом, заданный вектор и принятый вектор параллельны друг другу.
Когда есть информация о координатах вектора, если вы умножаете каждую координату этого вектора на заданное число, вы умножаете его на число.
Эта нотация представляет координаты вектора \(\vec.\)
Формулы применяющиеся при перемножении вектора и числа
В случае умножения вектора на число удобно использовать формулу умножения, предназначенную для решения плоских задач. При этом произведение вектора \(\vec=\left\;a_ \right\>\) и число k, рассчитанное по формуле:
Примеры проблем с решением
В этом случае рекомендуется использовать формулу для решения задач на площадь:
В случае пространственной задачи следует использовать следующую формулу:
Подставляя численные значения, получаем:
Умножение данного вектора на число \(\lambda =2\) по определению требует, чтобы каждая координата вектора \(\bar\) была умножена на это число. Таким образом:
Если вы хотите найти искомое произведение, умножьте каждую координату данного вектора \(\bar\) на число \(\lambda=-3\). Результатом умножения вектора на число является:
Согласно анализу рассмотренных закономерностей, действия с векторами похожи на действия с алгебраическими выражениями. В соответствии с этим принципом необходимо упростить следующие обозначения:
Сначала нам нужно раскрыть круглые скобки:
Тогда мы должны действовать аналогичным образом:
Существует сегмент AB. Точка C — центр отрезка, точка O — любая точка плоскости. Также \(\vec=\vec.\) и \(\vec=\vec.\) Вы должны это доказать:
Используя правило треугольника, вы можете выразить вектор \(\vec\) как сумму двух векторов:
Также обратите внимание на то, что:
В результате получается система из двух уравнений:
Затем нужно сложить уравнения системы:
Из того, что C — центр AB, следует, что молекулы этих векторов равны, но имеют разные направления. Поэтому сумма векторов является нулевым вектором. В результате:
Разделив обе части уравнения на 2, получим:
Мы должны распутать скобки и дать аналогичные скобки:
Докажите, что средняя линия трапеции и ее основания параллельны друг другу и что средняя линия трапеции равна половине суммы оснований.
Известно, что средняя линия трапеции соединена с ее боковыми сторонами. Основания трапеции параллельны друг другу. Согласно правилу многоугольника, мы можем выразить вектор \vec как сумму векторов:
С другой стороны:
В результате получается система уравнений:
Уравнения системы должны быть дополнены:
Векторы \(\vec\) и \(\vec\) имеют противоположные направления и вместе дают нулевой вектор, так как M — среднее AB, то есть единицы этих векторов равны, кроме того, они имеют противоположные направления. Аналогично, векторы \(\vec\) и \(\vec\) складываются в нулевой вектор. Так что у нас есть:
Затем мы можем разделить обе части уравнения на 2:
Результат доказывает, что средняя линия равна половине суммы оснований. Кроме того, прямая MN параллельна основаниям трапеции.
Насколько полезной для вас была эта статья?
Правила умножения вектора на число
Подумайте, как умножить вектор на число:

- Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
- Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
- Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
- Для умножения (АВ) (x; y; z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x; С*y; С*z).
Алгебраический и геометрический смысл действия

Каждая математическая операция имеет значение, которое варьируется от науки к науке. Давайте посмотрим, что дает нам такое умножение:
- Геометрический смысл : (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.
- Алгебраический смысл : (АВ) (x; y; z)*С — это новый (А1В1) с координатами равными (С*x; С*y; С*z).
- Физический смысл : уменьшение или увеличение в С раз силы действующей на тело или материальную точку.
Формулы умножения
При умножении проще использовать формулы, которые вы запомнили заранее и которые можно буквально автоматически применить к детали:
Начнем с физической задачи о силе, действующей на материальную точку. Рассмотрим силу, описываемую (AB) (57;63;28). Как изменяются координаты этой силы при ее десятикратном увеличении?
Прежде всего, обратите внимание, что направление силы не меняется, но сама сила увеличивается в десять раз. Если выразить это в координатах, то получится следующее:
10*(AV) (57;63;28) = (A1V1) (10*57;10*63;10*28) = (A1V1) (570;630;280).
Рассмотрим вторую задачу аналогичным образом: Как изменится сила, действующая на материальное тело, описываемое формулой (AB) (46;59;-43), если ее увеличить в-0,5 раз?
Прежде всего, обратите внимание, что знак константы отрицательный, так что направление самой силы меняется на противоположное. Если применить пункт 2 правил умножения, приведенных выше, то сразу станет ясно, что численное выражение силы уменьшится вдвое. Давайте произведем расчеты, используя шаблон:
-0,5*(AV) (46;59;-43) = (A1V1) (-0,5*46;-0,5*59;-0,5*(-43)) = (A1V1) (-23;-29,5;21,5).
Обратите внимание, что приведенные выше задачи решались для векторов в пространстве и с тремя координатами. В случае планарного размещения количество координат сокращается до двух, а в случае линейного размещения — до одной. Теперь рассмотрим математические примеры для этих случаев:
- 33*(CD) (11;10) = (C1D1) (33*11;33*10) = (C1D1) (363;330).
- -0,2*(АВ) (-0,3;25) = (А1В1) (-0,2*(-0,3); -0,2*25) = (А1В1) (0,06; -5).
- 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
- 0*(АВ) (65;-87) = (0).
Сложение векторов
Предположим, что объект первоначально находился в точке A, а затем был перемещен в точку B. Тогда удобно обозначить его перемещение вектором AB. Затем этот объект нужно переместить из точки B в другую точку C. Удобно использовать символ для обозначения объекта.
Из одной точки объект одновременно совершает два перемещения — из A в B и из B в C, которые можно представить в виде векторов:
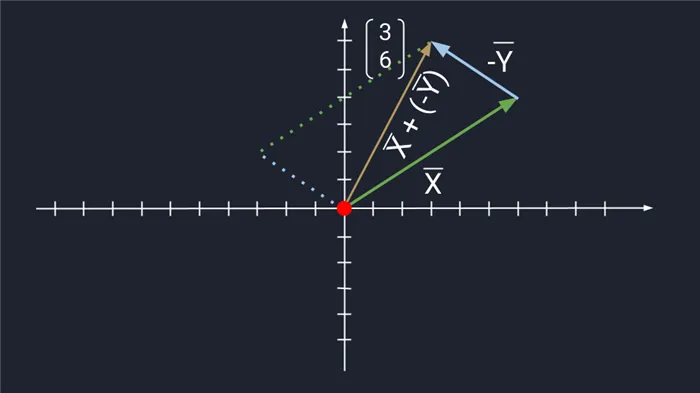
Этот пример показывает нам универсальное правило, по которому можно складывать векторы. Оно называется правилом треугольника.
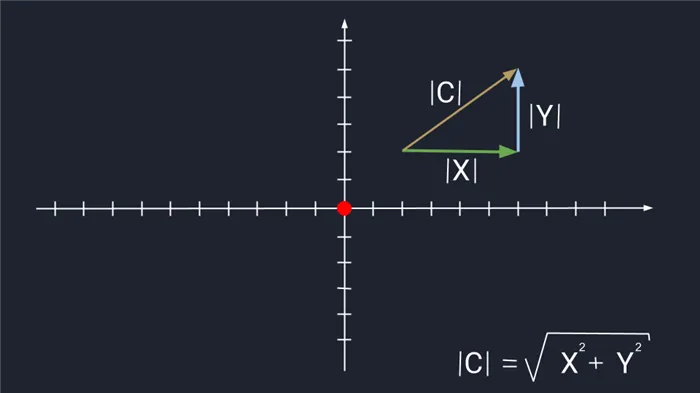
Согласно правилу треугольника, векторы можно складывать, если конец одного вектора совпадает с началом другого. Но что, если это не так? В этом случае достаточно взять вектор из конца одного вектора, который соответствует второму вектору:
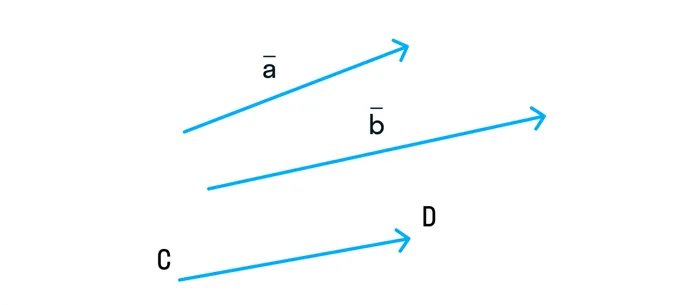
Задание. На рисунке вы видите два вектора. Запишите их сумму в тетрадь и найдите длину полученного вектора.
Решение. Переместите вектор b в конец вектора a. Затем найдите сумму двух векторов, используя правило треугольника (обозначьте этот вектор c):
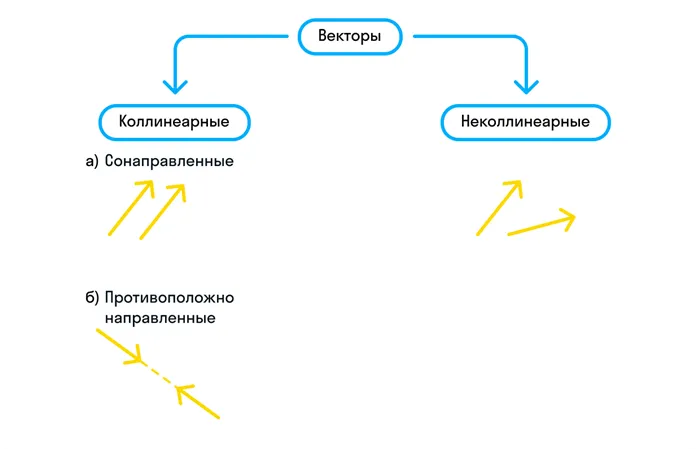
Теперь найдите длину результирующего вектора. Это гипотенуза правильного треугольника, а длины перпендикуляров в этом треугольнике можно определить по рисунку, они равны 4 и 6. Тогда длину гипотенузы можно найти по теореме Пифагора:
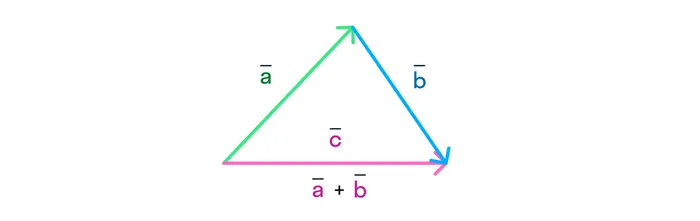
Рассмотрим отдельно случаи, когда добавляются коллинеарные векторы. В этом случае результирующая сумма будет слипаться с каждым сумматором. Если векторы имеют одинаковое направление, то длина конечного вектора будет равна сумме длин добавленных векторов:

Когда векторы складываются в противоположных направлениях, длина их суммы равна разности длин сложенных векторов.
По этой причине при решении простейших задач, связанных с движением судна в реке, скорость судна и скорость течения либо складываются, либо вычитаются. Дело в том, что в этих задачах векторы скорости корабля и текущей скорости складываются. Когда корабль идет по течению, эти векторы направлены в одну сторону, но когда он идет против течения, векторы направлены в противоположную сторону.
Задача. Корабль развивает скорость 12 км/ч в спокойной воде. Он движется по реке со скоростью 5 км/ч. Найдите скорость корабля. Найдите скорость корабля относительно берега, если:
(a) Корабль движется вниз по течению,
(b) Корабль плывет против течения,
(c) судно движется перпендикулярно течению.
Решение. Во всех случаях полная скорость судна является векторной суммой собственной скорости судна и течения реки:
Однако направления этих векторов различны. Найдем решение графически путем построения. В первом случае векторы являются однородными по условию:
Свойства сложения
Энергии с векторами во многом похожи на энергии с обычными числами. Помните, что в алгебре число не меняется, когда вы добавляете к нему ноль:
Даже добавление векторного нуля к вектору не меняет его:
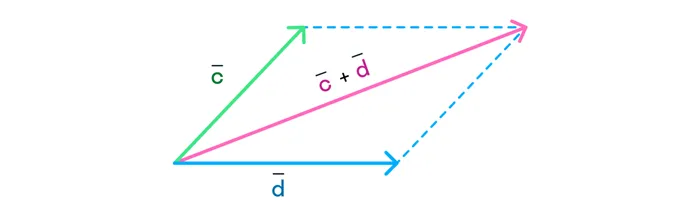
Применимо ли это правило к векторам? Оказалось, что да. Мы можем проверить это, построив параллелограмм, стороны которого являются сложенными векторами:
Мы видим, что диагональ параллелограмма является суммой векторов, соответствующих нижней и правой сторонам. Они называются векторами a и b, и в этом случае b прибавляется к a. Но в то же время, эта же диагональ является суммой векторов, соответствующих ее левой и верхней сторонам. Помните, что противоположные стороны параллелограмма равны и параллельны, поэтому они обозначаются вектором. В этом случае a уже было добавлено к b. Результат тот же, поэтому мы можем написать
На этом примере мы увидели, как работает другое правило сложения векторов, называемое правилом параллелограмма. Если есть два вектора, которые нужно сложить, мы можем удалить их из точки, а затем сложить полученную фигуру в параллелограмм.
Задача. Сложите векторы, показанные на рисунке, используя правило параллелограмма:

Решение. Нам нужно построить только параллелограмм, как показано на рисунке. Диагональ диагонали является искомым вектором:
Другой закон, используемый в алгебре, называется законом комбинаторики и заключается в следующем:
Оказывается, что это работает и для действий с векторами, т.е. аналогия сохраняется:
Здесь оранжевый вектор — это сумма красного (a) и синего (b) векторов. Если вы добавите зеленый вектор ( c ) к оранжевому вектору, вы получите фиолетовый вектор, который является суммой
Желтый вектор — это сумма синего и зеленого векторов. Мы видим, что фиолетовый вектор является суммой красного и желтого векторов, т.е. он является суммой

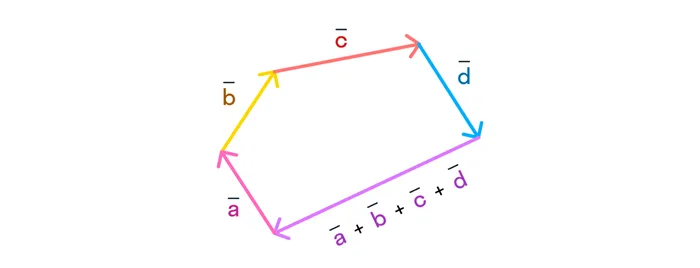
Можно добавить любое количество векторов. В этом случае необходимо добавить эти векторы один за другим, создавая «цепочку» векторов. Например, сложение 4 векторов, как показано на рисунке, выполняется следующим образом:

Этот способ сложения векторов называется правилом многоугольника. В силу закона взаимодействия векторы можно, конечно, прикладывать друг к другу в другом порядке, и результат будет тот же.
Задача. Добавьте векторы, показанные на рисунке, используя правило многоугольника. Выполните сложение двумя разными способами:
Вычитание векторов
Помните, что в алгебре вычитание представляется как обратная часть сложения. То есть, если для трех чисел отношение равно отношению трех чисел.
тогда разность между c и a равна b :
Аналогично вычитание понимается в векторной алгебре. Предположим, мы построим векторы a, b и c такие, что.

Этот пример показывает, как образуется разность двух векторов. На рисунке векторы c и a начинаются из одной точки, а вектор b, который является их разностью, проведен от конца вычитаемого вектора до конца вычитающего вектора.

Уменьшающий вектор — это вектор перед знаком минус в разности, а вычитающий вектор — это вектор после этого знака. Например, в обозначении
Вектор a — убывающий вектор, а вектор b — вычитающий вектор.
Задача. Нарисуйте в тетради разность между векторами, изображенными на рисунке:
Решение. Обратите внимание, что в условии не указан вектор, из которого нужно вычесть единицу. Это позволяет одновременно построить два ответа:

Легко видеть, что две получившиеся разности представляют собой противоположные векторы одинаковой длины. Такие векторы называются противоположными векторами.

Если мы сложим два противоположных вектора, то, естественно, получим нулевой вектор:
Противоположные векторы играют в векторной алгебре ту же роль, что и противоположные числа. Их удобно использовать для вычитания векторов. Напомним, что это соотношение справедливо для простых чисел:

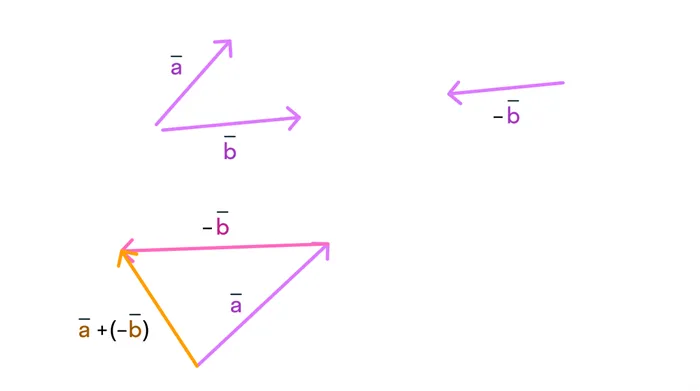
Поэтому операцию вычитания можно заменить операцией сложения, взяв вместо вычитаемого вектора противоположный ему вектор. Давайте рассмотрим этот метод на примере. Предположим, мы вычтем b из a :

На первом этапе постройте вектор, противоположный b :

Теперь нам остается только сложить a и (- b):

Наконец, нам удалось сформировать разность векторов a и b.
Уроки математики и физики для школьников и родителей

Для операции умножения вектора на число действуют следующие законы.





Умножение вектора на число с использованием координат вектора.
Когда вектор умножается на число, его координаты умножаются на это число, т.е. если



равны произведению числа k и соответствующих координат вектора.

Векторы часто помогают в изучении геометрических фактов: Для этого нам нужно научиться переводить геометрические факты на векторный язык, и наоборот, мы должны уметь переводить векторное выражение на геометрический язык. Предположим, нам нужно доказать, что прямые a и b параллельны.

которые принадлежат линиям a и b соответственно.


также могут иметь противоположные направления. Можно показать, что если векторы
параллельны, то из определения параллельности векторов следует, что прямые a и b параллельны. Вектор



Два вектора, исходящие из одной точки, лежат на одной прямой тогда и только тогда, когда один из векторов получается умножением на число из другого. Другими словами, точка X лежит на прямой AB тогда и только тогда, когда.

Уроки математики и физики (RU + UA)
- I. НАТУРАЛЬНЫЕ ЧИСЛА И ДРОБИ (RU + UA + EN)
- II. ПРОПОРЦИИ ПРОЦЕНТЫ МАСШТАБ (RU + UA)
- III. РАЦИОНАЛЬНЫЕ ЧИСЛА (RU + UA)
- IV. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ (RU + UA)
- V. КОРНИ (RU + UA)
- VI. ФУНКЦИИ И ГРАФИКИ (RU + UA + EN)
- VII. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ (RU + UA)
- VIII. ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
- IX. НЕРАВЕНСТВА (RU + UA)
- X. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (RU + UA)
- XI. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА (RU + UA)
- XII. ПЛАНИМЕТРИЯ (1) (RU + UA)
- XIII. ПЛАНИМЕТРИЯ (площади фигур) (RU + UA)
- XIV. СТЕРЕОМЕТРИЯ (1) (RU + UA)
- XV. СТЕРЕОМЕТРИЯ (2) (RU + UA)
- XVI. КОМБИНАТОРИКА (RU + UA)
- XVII. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ (RU + UA)
- XVIII. ВЕКТОРЫ (RU + UA)
- XIX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ (RU + UA)
- XX. ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ (RU + UA)
- КИНЕМАТИКА
- ДИНАМИКА
- WATCH YOUR MONEY!
Сайт содержит минимум информации о математике, поэтому любой ученик может пройти тесты с проходным баллом, если, конечно, решит все предложенные уроки. Этот сайт также поможет студентам, которые начинают изучать математику, и бабушкам, которые хотят помочь своим внукам изучать математику.
Каждый урок содержит краткую информацию о теоретической части и три практических упражнения с 12 примерами или задачами в каждом задании. Если хотите, вы можете представить свои ответы на упражнения в разделе комментариев для ознакомления. Сайт находится в постоянном развитии. Возможны методологические и математические ошибки.
Автор блога
Евгений Красавцев
- Урок 16. Абсолютная и относительная погрешность
- Урок 4. Первісна функція
- Урок 5. Периодичность тригонометрических функций
- Урок 12. Зростання і спадання функції
- Урок 27. Уравнение окружности
- Урок 10. Зрізана піраміда
- Урок 27. Піднесення до степеня алгебраїчних дробив
- Урок 21. Взаимное расположение графиков линейных функций
- Завдання 1. Зрізаний конус
- Урок 15. Приближённые вычисления








