Иногда ph-линии используются не для вычисления значений тригонометрических выражений, а для упрощения выражений. Из тождества sin 2 α + cos 2 α = 1 легко получить
Задача C1: тригонометрические уравнения и формула двойного угла
Очень часто в задачах GCSE Mathematics C1 учеников просят решить тригонометрическое уравнение, содержащее формулу двойного угла.
Сегодня мы снова разберем задачу C1, используя довольно нетрадиционный пример, который содержит и формулу двойного угла, и однородное уравнение. Например:
Решите уравнение. Найдите корни этого уравнения, принадлежащие интервалу:
sinx+ sin 2 x 2 — cos 2 x 2 ,x∈ -2 π ;- π 2
\sin x+\frac^>x>-\frac^>x>, x\in \lef t-2\text<>\!\!\!\pi\\!\!\!\text<>;-\frac\!\!\pi\!\!\text<>>\Okay.
Полезные формулы для решения
Прежде всего, напомню, что все задания C1 выполняются по одной и той же схеме. Сначала исходная конструкция должна быть преобразована в выражение, содержащее синус, косинус или тангенс:
sinx=a
\sin x=a
cosx=a
\cos x=a
tg x=a
tgx=a
В этом заключается основная трудность задачи С1. Дело в том, что каждое отдельное выражение требует своего вывода, который можно использовать, чтобы добраться от источника до таких простых конструкций. В нашем случае это формула двойного угла. Позвольте мне записать это:
cos2x= cos2x- sin2x
\cos 2x=^>x-^>x
Однако в нашем задании нет cos 2 x ^>x или sin 2 x ^>x, но есть sin 2 x 2 \frac<^>x>и cos 2 x 2 \frac.<^>x>.
Что теперь делать с этими расчетами? Давайте немного схитрим и введем новую переменную в нашу формулу для синуса и косинуса двойного угла:
x= t 2
x=\frac.
Мы записываем эту конструкцию с помощью синуса и косинуса:
cos2⋅ t 2 = cos 2 t 2 — sin 2 t 2
\cos 2\cdot \frac=\frac^>t>-\frac^>t>
Или другими словами:
Стоимость = cos 2 t 2 — sin 2 t 2
\cos t=\frac^>t>-\frac^>t>
Возвращаемся к нашему исходному заданию. Давайте sin 2 x 2 \frac^>x>мы двигаемся вправо:
sinx = cos 2 x 2 — sin 2 x 2
\sin x=\frac^>x>-\frac^>x>
Справа — точно такое же вычитание, которое мы только что написали. Нам нужно переставить его:
sinx=cosx
\sin x=\cos x
Теперь обратите внимание: Перед нами однородное тригонометрическое уравнение первой степени. У нас нет терминов, состоящих только из чисел и только из x x, у нас есть только синус и косинус. Более того, у нас нет квадратичных тригонометрических функций, но все функции возводятся в первую степень. Как решаются такие конструкции? Сначала предположим, что cosx=0 \cos x=0.
Подставим это значение в основное тригонометрическое тождество:
sin 2 x+ cos 2 x=1
^>x+^>x=1
sin 2 x+0=1
^>x+0=1
sinx=±1
\sin x=\pm 1
Если мы подставим эти числа, 0 и ±1, в исходную конструкцию, то получим следующее:
±1 = 0
\pm 1\text<>=\text.<>0
У нас полная ерунда. Поэтому предположение, что cosx = 0 \cos x = 0 ложно, cosx \cos x не может быть 0 в этом выражении. А если cosx \cos x не равен 0, то делим обе стороны на cosx \cos x:
sinx cosx = 1
\frac=1
sinx cosx =tg x
\frac=tgx
tg x=1
tgx=1
И вот мы имеем долгожданное элементарное выражение вида tg x=a tgx=a. Давайте хоть раз решим эту проблему. Это значение матрицы:
x= π 4 + π n,n ˜ ∈ Z
x=\frac\!\!\pi\!\!\text<>>>+\text<>\!\!\!\pi\\!\!\!\text<>n,n˜ в Z
Мы нашли корень, решили первую часть проблемы, то есть честно выиграли один из двух основных пунктов.
Теперь вторая часть: найдите корни этого уравнения, принадлежащие интервалу, точнее, интервалу
\ссылк и-2\текст<>\!\!\!\pi\\!\!\!\text<>;-\frac\!\!\pi\!\!\text<>>
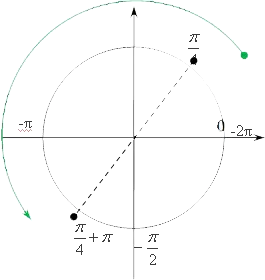
ight\. Предлагаю, как и в прошлый раз, решить это выражение графически, т.е. начертить окружность, отметить начало, т.е. 0, и концы отрезка:<>\!\!\!\pi\\!\!\!\text<>\!\!\!\!\pi\!\!\!\!\text<\pi>;-\frac
мы должны найти все значения, которые принадлежат к<>>>+\text<>\!\!\!\pi\\!\!\!\text<>\!\!\!\!\!\!\!\!\!\!\!\!\!<>>n.
Что нужно помнить для правильного решения
!
мы должны найти все значения, которые принадлежат к<>>>+\text<>\!\!\!\pi\\!\!\!\text<>\!\!\!\!\!\!\!\!\!\!\!\!\!
\ссылк и-2\текст<>\!\!\!\pi\\!\!\!\text<>;-\frac\!\!\pi\!\!\text<>>;-\frac\!\!\pi\!\!\text<>>\Okay.<>>+\text<>\!\!\!\pi\\!\!\!\text<>\!\!\!\!\!\!\!\!\!\!\!\!\!<>><\text>+\text<>\!\!\!\pi\\!\!\!\text<>\!\!\!\!\!\!\!\!\!\!\!\!
n. После некоторых простых измерений мы получили два определенных корня, т.е,<>>-\frac\!\!\pi\!\!\text
Доказательство формул двойного угла
что является ответом на вторую часть задачи, т.е. корни, ведущие к части
Все формулы двойного угла выводятся из формул для угловой суммы и разности тригонометрических функций.
Возьмем две формулы для суммы синуса и косинуса углов:
sin(\alpha+\beta)=« sin \alpha cos \beta+cos \alpha+ sin \beta` и `cos(\alpha+\beta)=«cos \alpha cos \beta-sin \alpha/ sin \beta`. Предположим, что `бета=\alpha`, тогда `sin(\alpha+\alpha)=« `sin \alpha\ cos \alpha+cos \alpha+cos \alpha\ sin \alpha=2 \ sin \alpha \ cos \alpha`, Аналогично, cos(\alpha+\alpha)=`cos \alpha-cos \alpha-sin \alpha-sin \alpha=cos^2 \alpha-sin^2 \alpha`, что доказывает формулу двойного угла для синуса и косинуса.
Два других уравнения для косинуса `cos \2\alpha=1-2 \sin^2 \alpha` и `cos \2\alpha=2 \cos^2 \alpha-1` сводятся к уже доказанному уравнению, если заменить в них 1 на `sin^2 \alpha+cos^2 \alpha=1`. Поэтому `1-2 \ sin^2 \alpha=«sin^2 \alpha+cos^2 \alpha-2 \ sin^2 \alpha=«cos^2 \alpha-sin^2 \alpha` и `2 \ cos^2 \alpha-1=«2 \ cos^2 \alpha-(sin^2 \alpha+cos^2 \alpha)=«`sos^2 \alpha-sin^2 \alpha`.
Чтобы доказать формулы для тангенса двойного угла и когерента, воспользуемся определением этих функций. Запишите `tg \2\alpha` и `ctg \2\alpha` как `tg \2\alpha=\frac` и `ctg \2\alpha=\frac`. Используя уже доказанные формулы двойного угла для синуса и косинуса, получаем `tg \2\alpha=\frac` и `ctg \2\alpha=\frac`.
Для тангенса разделите числитель и знаменатель последней дроби на `sin^2 \alpha`; для котангенса снова разделите на `sin^2 \alpha`.
Примеры использования формул при решении задач
Мы также рекомендуем посмотреть видео для закрепления теоретического материала:
Формулы двойного угла используются в большинстве случаев для преобразования тригонометрических выражений. Давайте рассмотрим некоторые практические применения этих формул для решения конкретных задач.
Пример 1. Проверьте правильность тождества двойного угла для «alpha=30^\circ».
Решение. В наших формулах используются два угла «альфа» и «2 альфа». Значение первого угла дано в предпосылке, второго угла соответственно `2\alpha=60^\circ`. Мы также знаем числовые значения всех тригонометрических функций этих углов. Давайте запишем их:
`sin 30^\\\circ=\frac 1 2`, `cos 30^\circ=\frac 2`, `tg 30^\circ=\frac 3`, `ctg 30^\circ=\sqrt 3` и
`sin 60^\circ=\frac 2`, `cos 60^\circ=\frac 1 2`, `tg 60^\circ=\sqrt 3`, `ctg 60^\circ=\frac 3`.
Тогда мы имеем
`sin 60^\circ=2 sin 30^\circ cos 30^\circ=2 \cdot \frac 1 2 \cdot \frac 2=\frac 2`,
cos 60^\circ=cos^2 30^\circ-sin^2 30^\circ=«`(\frac 2)^2 \cdot (\frac 1 2)^2=\frac 1 2«,
Это доказывает справедливость уравнений для угла, приведенных в условии.
Пример 2. Выразите `sin \frac 3` с помощью тригонометрических функций угла `\frac 6`.
Решение. Запишите угол синуса в виде `\frac 3=4 \cdot \frac 6`. Если мы дважды применим формулу для двойного угла, то сможем решить нашу задачу.
Сначала мы используем равенство синуса двойного угла: ` sin\frac 3=2 \cdot sin\frac 3 \cdot cos\frac 3`, теперь снова применим наши формулы для синуса или косинуса. В результате:
sin\frac 3=2 \cdot sin\frac 3 \cdot cos\frac 3=2 \cdot (2 \cdot sin\frac 6 \cdot cos\frac 6) \cdot (cos^2\frac 6- sin^2\frac 6)=« «4 \cdot sin\frac 6 \cdot cos^3 \frac 6-4 \cdot sin^3\frac 6 \cdot cos \frac 6«.
Формулы тройного угла
Ответ. sin\frac 3=««` «4 \cdot sin\frac 6 \cdot cos^3 \frac 6-4 \cdot sin^3\frac 6 \cdot cos \frac 6«.
Эти формулы, как и предыдущие, позволяют выразить угловые функции `3\alpha` через те же угловые функции `\alpha`.
Они могут быть доказаны с помощью уравнений угловой суммы и разности углов и хорошо известных формул двойного угла.
`sin \3\alpha= sin (2\alpha+ \alpha)=« `sin 2\alpha cos \alpha+cos 2\alpha sin \alpha=«`2 sin \alpha cos \alpha cos \alpha+(cos^2 \alpha-sin^2 \alpha) sin \alpha=«3 sin \alpha cos^2 \alpha-sin^3 \alpha«.
Замените `sin \3\alpha=3 sin \alpha cos^2 \alpha-sin^3 \alpha` `cos^2\alpha` на `1-sin^2\alpha` и получите \in \3\alpha=3 \ sin \alpha-4sin^3 \alpha`.
Также для косинуса тройного угла:
«cos \3\alpha= cos (2\alpha+ \alpha)= «cos 2\alpha cos \alpha-sin 2\alpha sin \alpha= «(cos^2 \alpha-sin^2 \alpha) cos \alpha-2 sin \alpha cos \alpha sin \alpha+= «cos^3 \alpha-3 sin^2 \alpha cos \alpha`.
Подстановка `cos \3\alpha=cos^3 \alpha-3 sin^2 \alpha cos \alpha` в `1-cos^2\alpha` дает `cos \3\alpha=4cos^3 \alpha-3 \ cos \alpha`.
Используя тождества, доказанные для синуса и косинуса, можно доказать тождества для тангенса и котангенса:
Чтобы доказать формулу для угла `4\alpha`, мы можем представить его как `2 \cdot 2\alpha` и попробовать формулу для двойного угла дважды.
Чтобы получить аналогичные уравнения для угла `5\alpha`, мы можем записать его как `3\alpha + 2\alpha` и применить тождества суммы и разности углов, а также двойного и тройного углов.
Доказательство формул двойного угла
Все формулы для других кратных углов выводятся аналогичным образом, но на практике они нужны редко.
Чтобы доказать формулы для двойных углов, вернемся к началу, к формулам сложения. Сначала рассмотрим формулу для синуса суммы, которая выглядит следующим образом:
Если мы предположим, что a = b, то получим:
(a + a)=\sin a * \cos a +\cos a * \cos a * \sin a = 2 * \cos a * \sin a
А также для косинуса:<2>\ \cos (a+a)=\cos a *\cos a *\cos a-\cos a-\sin a *\sin a =\cos ^<2>\альфа-\син ^
\альфа \
Таким образом, мы доказали формулы для синуса и косинуса двойного угла.
Остальные формулы: cos 2a = 1 — 2 * sin 2 a, cos 2a = 2 * cos 2 a-1, были выражены таким образом из-за тождества суммы квадратов, cos 2 a +sin 2 a = 1 вместо единицы. В результате получается следующее:
Формулы для двойного угла: 1 — 2 * sin 2 α = cos 2 α +sin 2 α — 2 * sin 2 α = cos2α — sin2α.
А также для третьих примеров формулы двойного угла. 2 * cos 2 α-1 = 2 * cos 2 α -( cos 2 α +sin 2 α ) = cos 2 α — sin 2 α.
Для доказательства формул для тангенса и котангенса двойного угла необходимо, чтобы выполнялось следующее равенство:
\operatorname 2 \alpha=\frac. \
Подставляя эти уравнения, получаем следующие выражения:
Разделим приведенные выше выражения на cos 2 α, где cos 2 α ≠ 0, а α имеет любое значение при определении тангенса угла α. Для второго показанного выражения мы также делим только на sin 2 α, и оно также ненулевое, а альфа имеет произвольное значение, при котором коинтегратор имеет смысл.

Получаем следующие формулы:
У вас нет времени на самостоятельное решение проблемы?
Как использовать формулы двойного угла
Наши эксперты могут помочь вам!
Рассмотрим, как применяются формулы для двойного угла при решении на примерах. Эти примеры помогут закрепить и понять ранее пройденный материал.
Чтобы проверить, применима ли формула двойного угла к значению тридцатиградусного угла альфа, необходимо применить тригонометрические функции для этих углов. Если α = 30°, то 2a = 60°.
Проверьте: sin60° = 2 * sin30° * cos30°cos60° = cos230° — sin230°.
Для доказательства формул для тангенса и котангенса двойного угла необходимо, чтобы выполнялось следующее равенство:
\оператор 60^=\frac
Поскольку мы знаем, что синус тридцати градусов равен одной секунде, косинус этого угла равен квадратному корню из трех, деленному на два, тангенс этого угла равен квадратному корню из трех, деленному на три, а котангенс равен квадратному корню из трех.
Так, синус двойного угла, то есть шестидесяти градусов, является корнем из трех, деленным на два; косинус равен одной второй; тангенс является корнем из трех; а котангенс — корнем из трех, деленным на три.
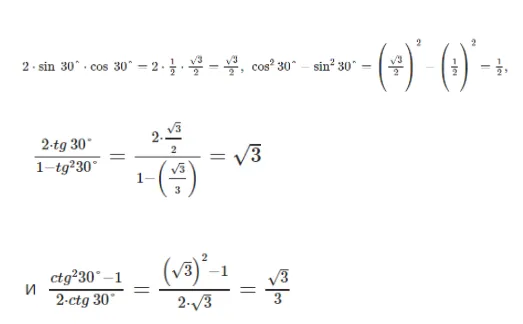
Получаем следующие выражения:
Проведя все расчеты, мы видим, что обоснованность угла альфа в тридцать градусов подтверждается.
Теперь мы понимаем, что применение формул тригонометрии двойного угла является модификацией тригонометрических выражений. Также стоит рассмотреть пример применения формул для двойных углов к случаю, когда угол не равен 2a. Например, возьмем значение \\\frac\. Поскольку у нас есть это значение, нам нужно преобразовать его для решения задачи, чтобы получить следующее.
\a=\frac: 2=\frac\, применяя это выражение, формула для косинуса двойного угла принимает следующий вид:
Пример:<при>Мы должны использовать тригонометрические функции, чтобы представить \a=\frac.
\frac\.

Формулы тройного угла и более углов
Решение:
\a=\frac: 2=\frac\, применяя это выражение, формула для косинуса двойного угла принимает следующий вид:
Пример:
sin 3α = sin ( 2 α + α ) = sin 2α * cos α + cos 2 α * sin α = 2 * sin α ⋅ cos α * cos α + ( cos 2 α — sin 2 α ) * sin α =.
=3 * sin α * cos 2 α — sin 3 α
Замените cos 2 α выражением 1 — sin 2 α, и формула, полученная ранее для тройного угла sin 3α = 3 * sin α * cos 2 α — sin 3 α, примет следующий вид: sin 3α = 3 * sin α * cos 2 α — sin 3 α = 3 * sin α — 4 * sin 3 α.
Проделаем то же самое с формулами для cos тройного угла:
cos 3α = cos ( 2 α + α ) = cos 2α * cos α — sin 2α *sin α = ( cos 2 α — sin 2 α ) * cos α — 2* sin α * cos α * sin α =
= cos 3 α — 3* sin 2 α * cos α
Замена sin 2 α на выражение для разности между единицей и косинусом, 1 — cos 2 α, дает следующую формулу: cos 3 α =
= -3 * cos α + 4 * cos 3 α
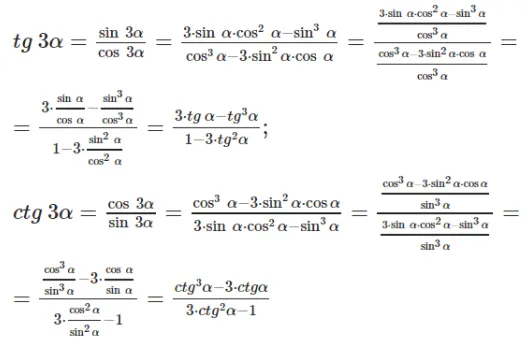
Теперь, когда мы знаем формулы синуса и косинуса для угла треугольника, мы можем вывести формулы тангенса и котангенса, подставив полученные выражения в формулы простых чисел:
Например, чтобы вывести формулу для угла 4a, для простоты предпочтительнее представить 4a как 2 * 2a, так что для выведения формулы для 4a нам придется использовать две формулы для двойного угла.
Чтобы вывести формулу для угла пятой степени, 5a, нужно представить 5a как сумму тройного и двойного угла, то есть 2a+3a.
Формулы двойного угла
В результате мы получаем выражение из суммы двух формул для двойного и тройного углов. Стоит отметить, что это же правило действует, когда нам нужно вывести формулу для половинного угла.
Что произойдет, если в формуле для синуса суммы заменить не два разных угла a и b, а два равных угла a и a? Вы получите формулу для синуса двойного угла:
Аналогично можно получить закон f для косинуса двойного угла:

Поэтому применяются следующие уравнения:

Задание. Вычислите sin 120° и s 120°.
Задание. Упростить
cos 2 t — cos 2 t = cos 2 t — (cos 2 t — sin 2 t) = cos 2 t — cos 2 t + sin 2 t = sin 2 t
Задание. Докажите, что функция
является периодическим и имеет период, равный π.
Решение. Мы используем квадрат суммы:
Таким образом, исходная функция может быть переписана следующим образом.
По определению, функция является периодической с периодом T, если выполняется условие y(x + T) = y(x). Поэтому подставьте x + π в нашу функцию:
Получаем, что y(x + π) = y(x), т.е. функция имеет период, равный π.
Задача. Выведите формулы для синуса и косинуса тройки.

Решение. Вам нужно использовать формулу для синуса суммы углов и заменить b на 2a:

Формулы понижения степени
Аналогично, вы получите значение f для косинуса угла тройки:
Если нам нужно узнать косинус угла, вдвое большего угла матрицы, мы используем значение f:
cos 2a = cos 2 a — sin 2 a — sin 2 a
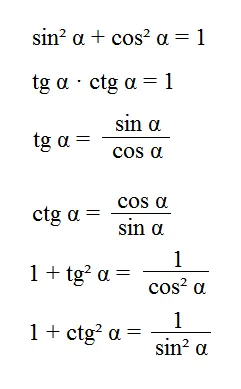
Но что, если нам нужно вычислить косинус угла, который в два раза меньше известного угла? Теперь попробуем преобразовать косинус двойного угла:
Это дает нам тождество, позволяющее определить косинус самого угла по косинусу двойного угла! В тригонометрии, однако, это тождество гораздо чаще записывается в обратном порядке:
и называется значением f с убывающей степенью. Действительно, левая часть — это косинус в квадрате, а правая — косинус без квадрата, но он вычисляется из угла 2a, а не из α.

Попробуем найти аналогичную формулу для синуса. Для этого мы используем основное треугольное тождество:
Мы можем использовать эти f-линии для вычисления треугольных функций для некоторых малых углов. Итак, ранее мы вычислили формулу для разности синусов и обнаружили, что

Мы представили угол 15° как 45° — 30°. Но как вычислить 7,5°? Этот угол нельзя представить как разность или сумму известных табличных углов (0°, 30°, 45°, 60° и 90°), но полезно использовать убывающую степень ф-лы. Фактически, 2-7,5° = 15°. Тогда мы можем написать:
Мы нашли cos 2 7,5°. Чтобы найти 7,5°, нужно взять квадратный корень:

Поскольку угол 7,5° принадлежит первой четверти, его косинус должен быть положительным, поэтому мы можем написать:
Мы видим, что это довольно неудобное выражение. Используя уравнение сокращения, мы также можем определить косинус половины угла, то есть 3,75°, но результат будет еще более неудобным.
Задача. Вычислите sinπ/8.

Решение. Угол π/4 является столовым углом (его градусная мера равна 45°), поэтому мы можем написать:
Формулы приведения
Эти примеры показывают, что тригонометрические функции многих нестандартных углов могут быть выражены через квадратные корни. Возникает вопрос, каждую ли тригонометрическую функцию можно выразить таким образом. Оказалось, что нет. Например, sin 10° нельзя найти ни в одной тригонометрической таблице, какой бы подробной она ни была. Мы не будем это доказывать, но значение не может быть выражено арифметическими операциями и корнями. Однако существуют методы аппроксимации, которые можно использовать для вычисления значения тригонометрических функций с произвольной точностью.
Вы могли заметить, что синус и косинус имеют одинаковое значение для углов, сумма которых равна 90°. Например: sin30° = cos60° = 1/2 и поэтому 30° + 60° = 90°. Мы также знаем, что sin 45° = cos 45° (45° + 45° = 90°) и sin60° = cos30° (60° + 30°). В чем причина такой закономерности и применима ли она к нестандартным углам?
Используя уравнение синусоидальной разности, мы можем написать
Полученная формула sin (90° — a) = cosα называется формулой приведения. Чтобы вывести ее, мы использовали тот факт, что sin 90° = 1 и cos 90° = 0, поэтому формула очень проста. Синусы и косинусы других углов, кратных 90° (или кратных π/2, если вы измеряете углы в радианах), также равны 0, 1 или — 1, поэтому для них также можно вывести аналогичные простые линии f, например:
Можно написать многие десятки подобных пхп! Не обязательно учить их все наизусть, так как существует специальная мнемоника, позволяющая написать нужную ф-лу.
Предположим, что существует тригонометрическое выражение вида
где f — тригонометрическая функция (sin; cos; tg; ctg)
k- угловое кратное π/2 (π/2, π, 3π/2, 2π).
Мы хотим заменить ее другой функцией f, только с углом a. На первом этапе мы рассматриваем сумму k. Если она кратна π (- π, π, 2π), то функция f остается неизменной. Если сумма k является числом π/2 или 3π/2, то функция f должна быть преобразована в так называемую кофункцию (преобразование синуса в косинус, тангенса в котангенс и наоборот).
Затем нужно определить знак перед новой функцией f. Для этого предположим, что a — острый угол, т.е. принадлежит первой четверти. Исходя из этого предположения, мы исследуем, на какую четверть приходится угол k ± α и какое значение принимает там исходная тригонометрическая функция. Если оно отрицательное, поставьте знак минус перед новой тригонометрической функцией. В противном случае вам не нужно ничего вводить.
Лучше всего изучать алгоритм на примерах.
Задача. Упростите выражение на s ( π/2 + a).
Решение. Первым шагом является рассмотрение суммы под символом косинуса. Это число равно π/2. Оно НЕ кратно π, поэтому нам нужно преобразовать косинус в синус:
Второй шаг — решить, ставить ли перед синусом знак минус. Если α — острый угол, то угол (π/2 + α) попадает во вторую четверть:
Во второй четверти косинус отрицательный, поэтому перед синусом нужно поставить знак минус:
cos (π/2 + α) = — sinα<α<90°. Предположение об остроте угла – это лишь часть мнемонического правила для составления формул приведения, позволяющая быстро определить, надо ли в ней перед тригонометрической функцией ставить знак минус или не надо.
Важные замечания. В этом примере мы «предположили», что угол α острый, чтобы вывести формулу уменьшения. В результате мы смогли получить формулу cos (π/2 + α) = — sinα. Заметим, однако, что полученная нами формула применима к любому значению угла α, а не только к 0°.
Это мнемоническое правило работает с абсолютной точностью, но должно быть ясно, что для строгого вывода формул сокращения следует использовать формулу суммы косинусов.
cos (π/2 + α) = cosπ/2 cos α — sin π/2 sin α = 0-cos α — 1-sin α = — sin α
Тождества при других значениях
Используя формулу уменьшения, мы получили тот же результат. В этом случае предположение об остроте угла α не является необходимым, т.е. формула справедлива для любого α. На практике, однако, оказывается, что люди просто не могут запомнить формулу для суммы косинусов. Поэтому, чтобы «упростить жизнь», студентам объясняется относительно простая мнемоника.
На практике студенты-математики вузов сталкиваются с задачами, для решения которых используются формулы для тройного, четверного и других углов. Они основаны на тригонометрических функциях. Для их выведения используются формулы сложения двойных углов: sin3a = sin (2a+a) = 3-sinα-cos2a — sin3a.

Замена cos2α на 1-sin2α дает формулу в новом виде: sin3α = 3-sinα-4-sin3α. Формула для косинуса угла триплета имеет аналогичную форму: Косинус3a = Косинус (2a+a) = Косинус3a — 3-sin2a-syn2a-synitonea.
Замена sin2a на 1-cos2a дает формулу вида cos3a = -3-cosa+4-cos3a. С помощью этих уравнений формула угла треугольника для тангенса и котангенса преобразуется: tg3α = sin3αcos3α = ctg3α — 3-ctgα3-ctg2α — 1.
Формулы для четвертой степени выводятся по той же методике. Значение 4a должно быть представлено как 2-2a. Равенство достигается за счет двойного использования FDU. Значение угла 5a представляется как 3a+2a для получения равенства пятой степени.
Область применения
Эта сумма позволяет использовать формулы для двойных и тройных углов для преобразования в конечный результат. Различные степени тригонометрических функций преобразуются по аналогичной схеме, но редко используются в тригонометрии.

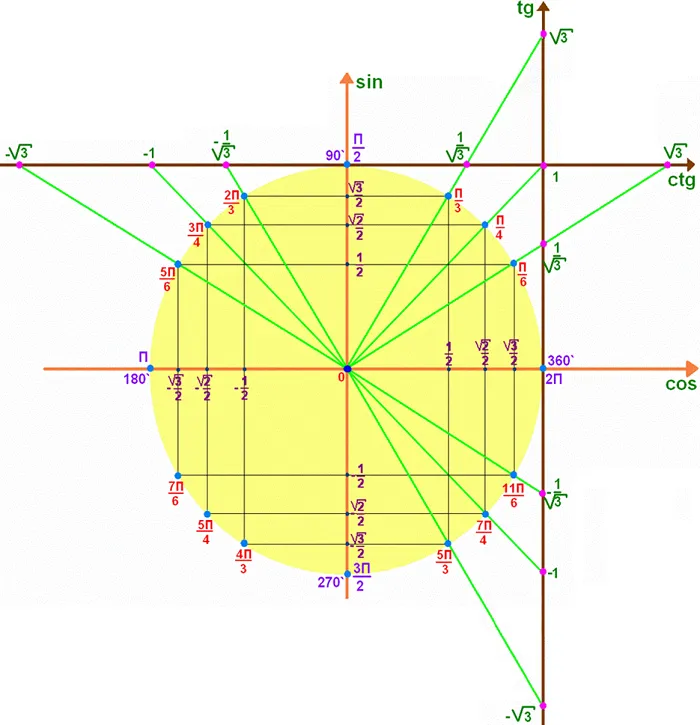
Для определения значения тригонометрической функции (TF) рассматривается круг радиусом 1 с диаметрами, перпендикулярными друг другу. Для расчета необходимы дуги любой длины из точки, принадлежащей окружности. Они положительны, если установлены против часовой стрелки.
Отрицательные значения берутся из тех, которые установлены по часовой стрелке. Если конец дуги имеет длину f, то проекция радиуса на любой диаметр принимает значение косинуса дуги. Термин аргумент относится к числу, которое геометрически считается f или радиальной мерой угла. Если аргументом TF является угол, то его значение также выражается в градусах.
Оказывается, что величина острых углов больше нуля, но меньше p/2. Для таких значений TF принимается как отношение перпендикуляра к гипотенузе. Эти элементы принадлежат прямому треугольнику. Название связано с углом в 90 градусов. Теорема Пифагора также используется для решения задач с тригонометрическими функциями, основанными на свойстве правильного треугольника: квадрат гипотенузы равен сумме квадратов перпендикуляров.
Дуга делит круг на несколько частей. Углы в первой четверти больше нуля, во второй четверти косинус меньше, а синус больше, в третьей четверти TF меньше 0, а в четвертой четверти взяты значения, противоположные второй четверти. Вам понадобится компас, чтобы начертить окружность, и транспортир, чтобы измерить углы.
Как успешно подготовиться к ЦТ по физике и математике?
Чтобы получить точный чертеж, рекомендуется записать данные на графической бумаге или в блокноте.
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Для успешной подготовки к КТ по предметам физика и математика необходимо выполнить, в частности, три основных требования:
Нашли ошибку?
Успешное, тщательное и ответственное выполнение этих трех заданий, а также ответственное выполнение заключительных практических тестов позволит вам получить на экзамене CT отличную оценку — наивысший балл, который вы можете получить.
Если вы считаете, что нашли ошибку в учебном материале, пожалуйста, отправьте нам электронное письмо (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название или номер предмета или экзамена, номер задания или отрывок текста (страницу), в котором вы подозреваете ошибку. Также объясните, в чем, по вашему мнению, заключается ошибка. Ваше письмо не останется незамеченным, и ошибка будет либо исправлена, либо мы сообщим вам, почему это не ошибка.
Материалы данного сайта или любая их часть не могут быть использованы в коммерческих целях, а также скопированы, перепечатаны, переизданы или воспроизведены в любой форме. Нарушения прав владельцев авторских прав будут преследоваться по закону. Читать далее.








