Теперь рассмотрим треугольники ACD и CBD. Широко используется латеральный CD. AC = BD и AD = CB из того, что было доказано ранее. Таким образом, треугольники ACD и CBD равны с третьим знаком.
Третий признак равенства треугольников
Третий знак — последний из основных знаков равенства треугольников. Он считается самым простым, поскольку основан на равенстве трех сторон. То есть, если три стороны треугольника равны трем сторонам другого треугольника, то эти треугольники равны. В этой формулировке нет углов, поэтому перепутать их гораздо сложнее, чем в предыдущих двух пунктах.
Давайте вернемся к рисунку. KLM и K1L1M1 являются треугольниками. По условию, KL = K1L1, LM = L1M1, MK = M1K1. Соответственно, эти треугольники равны по трем сторонам или по третьему признаку.
Теорема о третьем признаке равенства треугольников
Теперь докажем теорему. В этом случае доказательство опирается не на метод суперпозиции, а на основные геометрические законы и свойства треугольника. Сначала возьмите любые две равные стороны (например, KL и K1L1) этих треугольников и совместите их так, чтобы точки M и M1 лежали на противоположных сторонах KL. Начертите отрезок MM1. Есть три возможных варианта:
Первый случай
KMLM1 — выпуклый четырехугольник. Отрезок MM1 лежит внутри четырехугольника KMLM1.
Рассмотрим треугольник MLM1: ML = M1L1 или LMM1 и LM1M, по условию, равны углам при основании равнобедренного треугольника. Далее рассмотрим треугольник KMM1. KM = KM1 по условию KMM1 и KM1M равны как углы при основании равнобедренного треугольника.
Теперь обратимся к треугольникам KML и KM1L. Угол KML = KMM1 + M1ML и угол KM1L = KM1M + MM1L. Мы знаем, что KMM1 = KM1M и M1ML = MM1L; следовательно, углы KML и KM1L равны. Тогда треугольники KML и KM1L равны друг другу по двум сторонам и углам. Доказан первый случай теоремы.
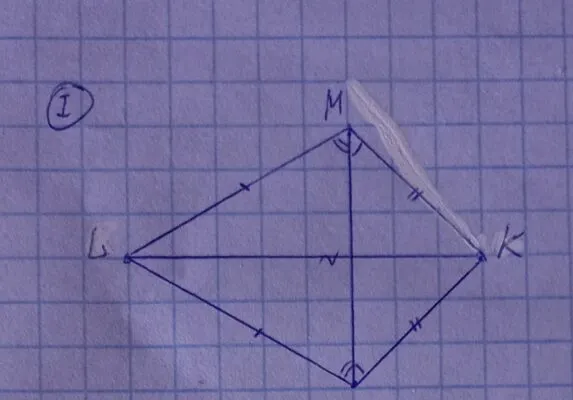
Второй случай
KMLM1 — невыпуклый четырехугольник. Отрезок MM1 лежит вне четырехугольника KMLM1.
Рассмотрим треугольник MM1L. ML = M1L, поэтому углы LMM1 и MM1L равны, так как лежат на основании равнобедренного треугольника. Затем рассмотрим треугольник MM1K. MK = KM1, поэтому KMM1 = KM1M, так как углы лежат на основании равнобедренного треугольника.
Теперь рассмотрим треугольники LMK и LM1K: угол LMK = LMM1 — KMM1 и угол LM1K = LM1M — KM1M. Поскольку LMM1 = MM1L и KMM1 = KM1M, углы LMK и LM1K также равны. Кроме того, треугольники KML и KM1L равны в соответствии с первым условием равенства треугольников, то есть ML = M1L и KM = KM1.
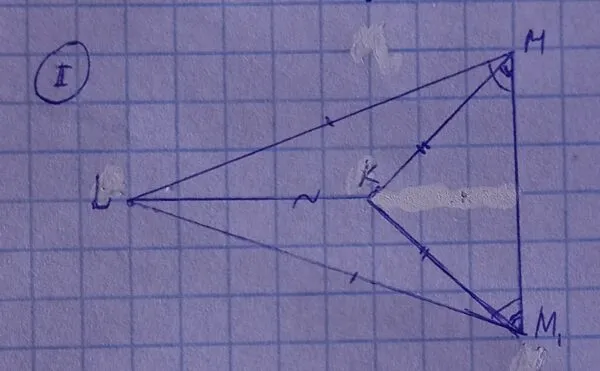
Третий случай
Отрезок MM1 совпадает со сторонами KM и KM1, т.е. MM1L — треугольник.
Этот случай является самым простым и легко доказуемым. Итак, рассмотрим треугольник MLM1: ML = M1L, а углы LMM1 и LM1M равны углам при основании равнобедренного треугольника.
Рассмотрим треугольники KLM и KLM1: KM = KM1 и ML = M1L в соответствии с конвенцией, LMM1 = LM1M в соответствии с тем, что было доказано ранее. Таким образом, треугольники KML и KM1L равны в соответствии с первым символом равенства треугольников.
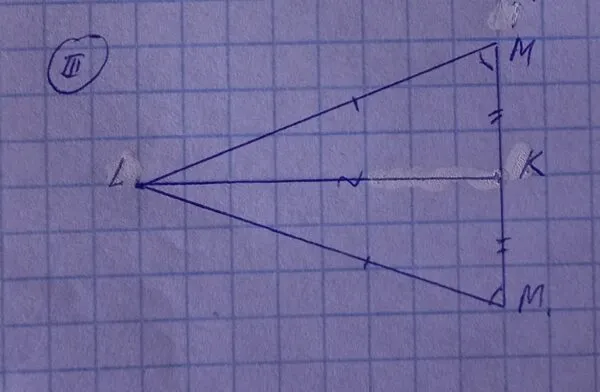
Решение задач
Чтобы углубить тему, стоит перейти к практической части — решению проблем.
Задание 1
Используя диаграмму, определите количество пар равных треугольников на чертеже.
Сначала рассмотрим треугольники AOB и COD; AB = CD, OB = OC, OA = OD. Следовательно, эти треугольники равны по трем сторонам.
Теперь рассмотрим треугольники ABC и BCD. BC — общая сторона, AB = CD по условию. AC = AO + OC и BD = OB + OD. Известно, что OB = OC и OA = OD. Поэтому BD = AC. Следовательно, треугольники ABC и BCD равны в соответствии с третьим принципом равенства треугольников.
Наконец, давайте рассмотрим треугольники ABD и ACD. AD — общая сторона, AB = CD — условная. В предыдущем элементе мы доказали равенство сторон AC и BD. Это означает, что треугольники ZCD и ABD равны по трем сторонам.
Это были все пары равных треугольников, показанные на этой диаграмме.
Ответ: Три пары: AOB и COD, ABC и BCD, ABD и ACD.
Задание 2
Найдите пары равных треугольников, используя данные на диаграмме.
Рассмотрим треугольники ABD и BEC. AD = EC, AB = BC и BD = BE — это условные обозначения. Следовательно, эти треугольники равны по трем сторонам.
Затем рассмотрим треугольники ABE и DEC: BD = BE по условию, AB = BC по тому же условию. AE = AD + DE, и DC = DE + EC. Поскольку AD = EC (по условию), AE = DC. Тогда треугольники ABE и DBC равны в соответствии с третьим символом равенства треугольников.
Ответ: две пары равных треугольников: ABD и BEC, ABE и DEC.
Задание 3
Используйте данные на следующем рисунке для определения угла альфа. В дополнение к данным на рисунке известно, что BC = FD.
Рассмотрим треугольники ABC и FDE; AB = DE, также BC = FD по условию. AC = FC + AF и FE = FC + CE. Поскольку AF = CE, AC = FE. Таким образом, эти треугольники равны по третьему символу равенства треугольников. Угол DFE = 180 — 115 (так как сумма смежных углов равна 180 градусов) = 65. Углы DFC и BCA равны как соответствующие элементы равных треугольников. Тогда угол BCA = 65 градусов, а угол BCE (или угол альфа) = 180 — 65 = 115 градусов.
Ответ: Угол альфа равен 115 градусам.
Задание 4
Используя данные рисунка, докажите, что BD — биссектриса угла B.
Рассмотрим треугольники ABD и BDC. BD — общая сторона, а AB = BC и AD = DC — условные знаки. Тогда треугольники ABD и BDC равны по трем сторонам.
В данном случае углы ABD и DBC равны как соответствующие элементы в равных треугольниках. Поскольку угол B равен сумме углов ABD и DBC, а они равны, BD — биссектриса угла B.
Задание 5
Даны треугольники ABC и A1B1C1, которые являются равносторонними по соглашению. Докажите, что эти треугольники равны.
Эту проблему можно решить и без рисунка.
Поэтому обозначим сторону треугольника ABC как a, а сторону треугольника A1B1C1 как a1. Тогда Pabc = 3 * a, а Pa1b1c1 = 3 * a1. Поскольку по условию Pabc = Pa1b1c1, следует, что a = a1.
Поскольку, согласно определению равностороннего треугольника, все стороны треугольника ABC равны сторонам треугольника A1B1C1. Тогда эти треугольники равны по трем сторонам.
Задание 6
Даны треугольники ABC и A1B1C1. BD — медиана треугольника ABC, а B1D1 — медиана треугольника A1B1C1. AB = A1B1, BC = B1C1 и BD = B1D1. Нам нужно доказать равенство этих треугольников.
Во-первых, расширьте сегмент BD. Отметьте точку E так, чтобы DE = BD. Постройте отрезок EC. Аналогично для треугольника A1B1C1: Развернем отрезок B1D1. Отметьте точку E1 так, чтобы D1E1 = B1D1. Постройте отрезок E1C1.
Первый признак равенства треугольников
Теорема 1. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1C1(Рисунок 3). Пусть AB = A1B1AC = A1С1и &angle? A = &угол? A1. Мы хотим доказать, что
Поскольку ∠ A = ∠ A1тогда треугольник ABC можно положить на треугольник A1B1C1так, чтобы вершины A и A1совпадают, а AB и AC совпадают с A1B1и А1C1.
Так как по теореме AB = A1B1AC = A1С1тогда сторона AB сопряжена со стороной A1B1а сторона AC конгруэнтна стороне A1С1Тогда Б и В являются1, C и C .1. Следовательно, сторона BC выровнена со стороной B.1C1. То есть, треугольники ABC и A1B1C1полностью конгруэнтны. Теорема доказана.
Второй признак равенства треугольников
Теорема 2: Если сторона и два смежных угла одного треугольника равны стороне и двум смежным углам другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1С1(рисунок 4), где AB = A1B1, &angle? A = &угол? A1, &angle? B =&&&угол? B1. Мы хотим доказать, что
Поместите треугольник ABC на треугольник A1B1С1так, чтобы вершина A была конгруэнтна вершине A.1Сторона AB совпадает со стороной A.1B1(по теореме AB = A1B1), а вершины C и C1лежат по одну сторону от линии A1B1.
Поскольку ∠ A = ∠ A1и &angle? B =& угол? B1то сторона AC подключается к линии A1C1а сторона BC пересекается с B1С1. Тогда вершина C лежит на прямой A1C1и на B1C1. То есть, она расположена на пересечении этих лучей, а вершина C задана общей точкой лучей A1C1и Б1C1т.е. вершина C1. Поэтому стороны AC и A1C1, BC и B1C1. То есть, треугольники ABC и A1B1С1полностью конгруэнтны, т.е. равны. Теорема доказана.
Третий признак равенства треугольников
Теорема 3. Если три стороны одного треугольника равны трем сторонам другого треугольника, то эти треугольники равны.
Доказательство. Рассмотрим треугольники ABC и A1B1С1. Пусть AB = A1B1AC = A1C1и BC = B1C1. Докажите, что ABC в треугольнике A1B1С1так, чтобы вершина A была конгруэнтна вершине A.1Вершина B совпадает с вершиной B.1и вершины C и C1лежат по разные стороны от линии A1B1.
Возможны три варианта: CC1проходит через угол ACB (рис. 6); радиус CC1совпадает с одной из сторон угла ACB (рис. 7); луч CC1проходит вне угла ACB (рис. 8). Давайте рассмотрим эти три случая по отдельности.
Случай 1 (Рисунок 6): Так как по теореме AC = A1C1и BC = B1C1тогда треугольники A CC1и B CC1являются равнобедренными. Тогда &угол;1=&угол;2 и &угол;3=&угол;4 и, таким образом:
| . |
AC = A1C1, BC = B1C1∠ ACB = ∠ A1C1B1и в соответствии с первым принципом равенства треугольников.
Вариант 2 (рис. 7): Так как по теореме AC = A1C1и BC = B1C1тогда треугольник BC1является равнобедренным. Тогда &угол;1=&угол;2: AC = A1C1, BC = B1C1&угол;1=&угол;2 и согласно первому принципу равенства треугольников
Вариант 3 (рис. 8). Так как по теореме AC = A1C1и BC = B1C1тогда треугольники A CC1и B CC1являются равнобедренными. Тогда &угол;1=&угол;2 и
| . |
AC = A1C1, BC = B1C1. Теорема доказана.








