Точка пересечения высот треугольника называется ортоцентром и традиционно обозначается латинской буквой H. «Ортос» в переводе с греческого означает «прямой», «правильный». Ортоцентр может находиться внутри или снаружи фигуры. Его положение зависит только от самой фигуры и не зависит от порядка расположения сторон и вершин.
Определение и свойства высоты треугольника
В этом посте мы рассмотрим определение высоты треугольника, покажем, как она выглядит в зависимости от типа треугольника, и перечислим ее основные свойства.
- Определение высоты треугольника
- Высота в разных видах треугольников
- Свойства высоты треугольника
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
Определение высоты треугольника
Высота треугольника — это перпендикулярная линия, которая опускается из вершины фигуры на противоположную сторону.
Основание высотомера — это точка на противоположной стороне треугольника, которая пересекает высотомер (или точка, где пересекаются их продолжения).
Обычно высота обозначается буквой h (иногда также как ha— что означает, что он соединен со стороной a ).
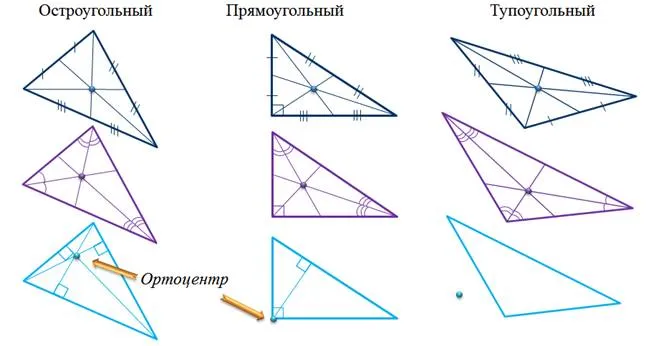
Высота в разных видах треугольников
В зависимости от типа формы, высота может быть разной:
- проходить внутри треугольника (в остроугольном △);
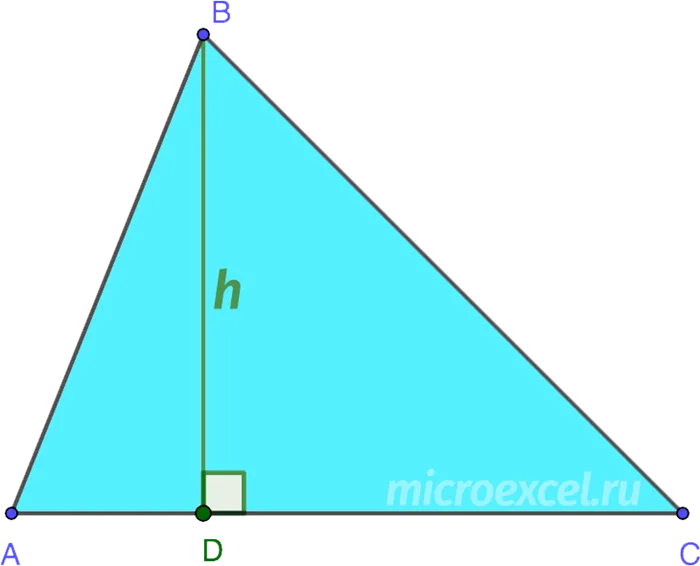
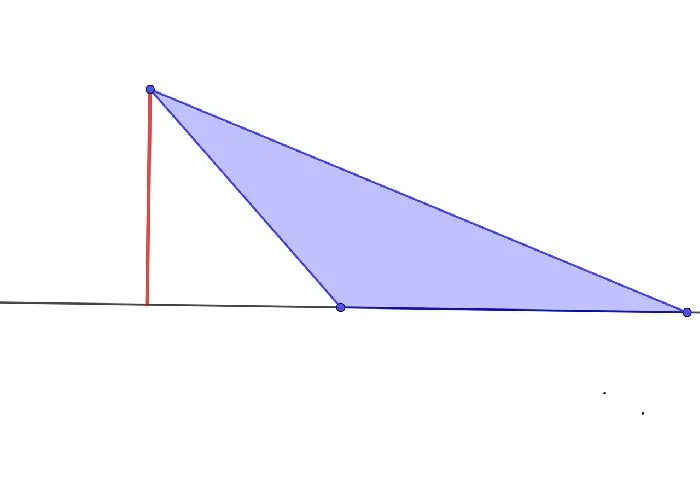
- проходить за рамками треугольника (в тупоугольном △);

- являться одним из катетов (в прямоугольном △), за исключением высоты, проведенной к гипотенузе.
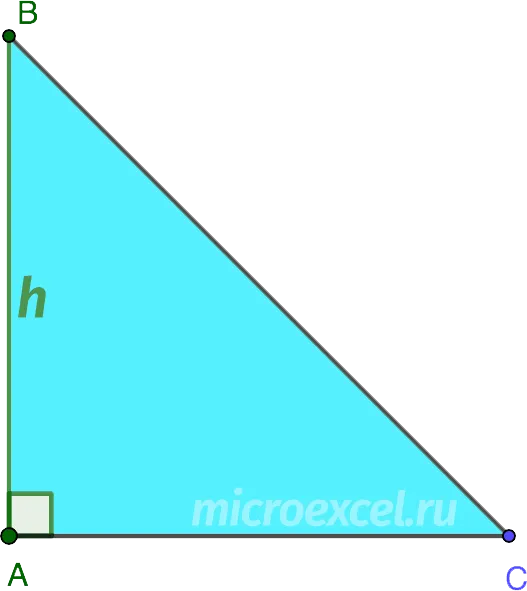
Высота
Что такое высота? Высота — это перпендикуляр, проведенный из вершины треугольника к линии, содержащей противоположную сторону треугольника (может случиться так, что высота попадает на продолжение стороны, как в тупоугольных треугольниках).
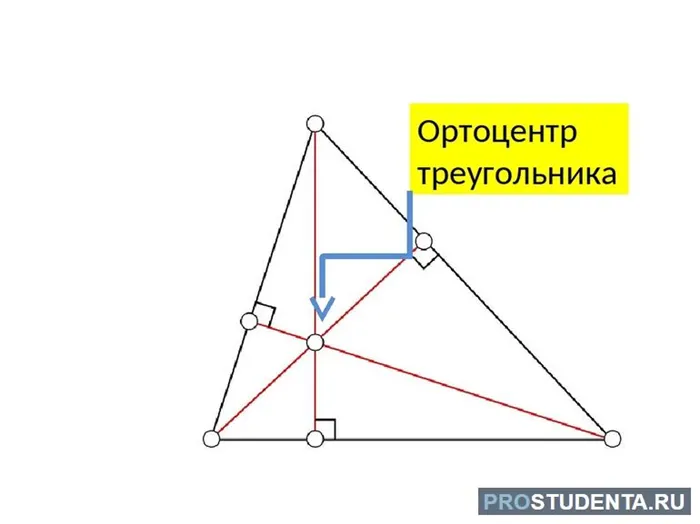
Точка пересечения высот
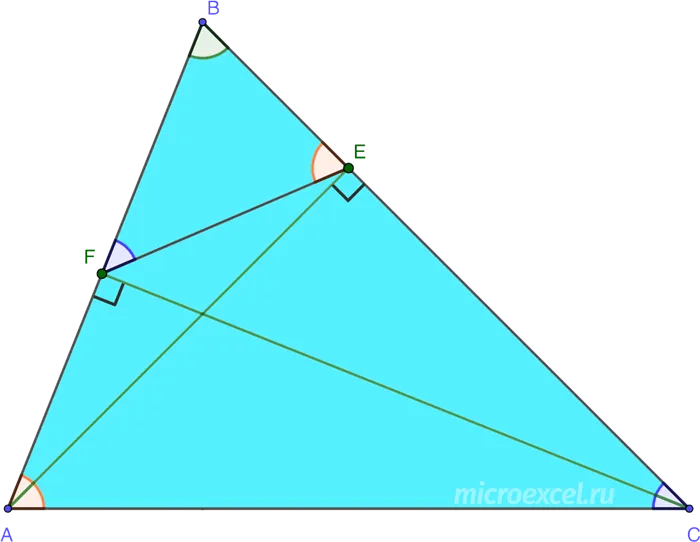
Каждый треугольник имеет три высоты, которые всегда пересекаются в одной точке. Эта точка является одним из трех центров треугольника и называется ортогональным центром.
С древнегреческих времен приставка «орто» использовалась для обозначения вертикальной линии. Вертикальные линии были названы ортогональными.
В зависимости от типа треугольника существует три варианта ортоцентра:
- Внутри фигуры. В остроугольных треугольниках точка пересечения высот всегда находится внутри фигуры. Это обусловлено тем, что все высоты в таком треугольнике внутренние.
- Совпадает с вершиной. Этот случай характерен для прямоугольных треугольников. В таких треугольниках две из трех высот будут совпадать со сторонами. Если быть точнее, то совпадающие стороны это катеты. Остается одна высота, которая будет опускаться из вершины при остром угле. Именно эта вершина и будет ортоцентром треугольника.
- Вне фигуры. Внешнее расположение ортоцентра возможно только в тупоугольном треугольнике. Для того, чтобы получить ортоцентр такого треугольника, иногда потребуется продлить высоты до пересечения с внешней высотой. Почему?
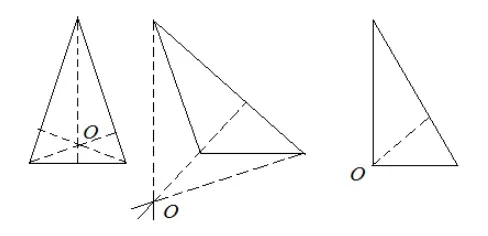
Поскольку внешняя высота находится вне треугольника, а затем одна из сторон опускается, две внутренние стороны всегда ограничены треугольником. Поэтому найти правильный центр тупоугольного треугольника без дополнительных построений невозможно.
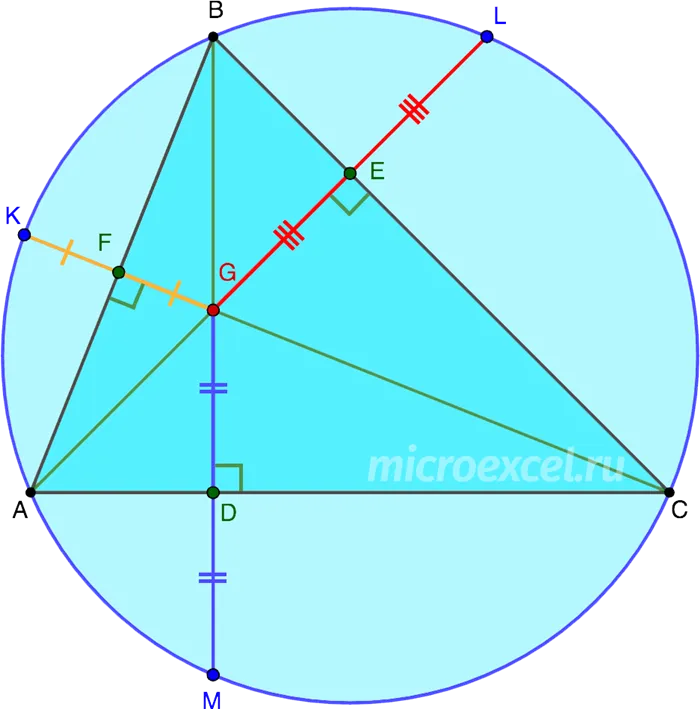
Золотое сечение треугольника
Золотое сечение треугольника — это маленький треугольник внутри фигуры, который определяется как пересечение трех центров треугольника.
Тремя центрами треугольника являются:
- Точка пересечения биссектрис
- Точка пересечения высот
- Точка пересечения медиан.
Золотое сечение иногда может вырождаться в прямую линию или даже точку. В равнобедренном треугольнике точки пересечения высот и медиан совпадают, поэтому для построения золотого сечения требуется всего 2 точки, и золотое сечение вырождается в отрезок.
Существует целая онлайн-энциклопедия о центрах треугольника. Список треугольных центров и их свойств был начат Карлом Камберлингом в 1994 году. Онлайн-ресурс пополняется все новыми и новыми данными по мере их обнаружения в высшей математике. В школьном курсе рассматриваются только 3 центра треугольника.
В правильном треугольнике каждая высота совпадает с соответствующей средней линией, биссектрисой и высотой. Таким образом, все три центра треугольника совпадают, а золотое сечение треугольника является точкой.
Обратите внимание, что уравнение пересечения высот треугольника не может быть составлено. Вы можете составить уравнение только прямой линии. Например, задайте два уравнения для высот, установите их равенство и найдите координату точки пересечения.
Информация об ортоцентре
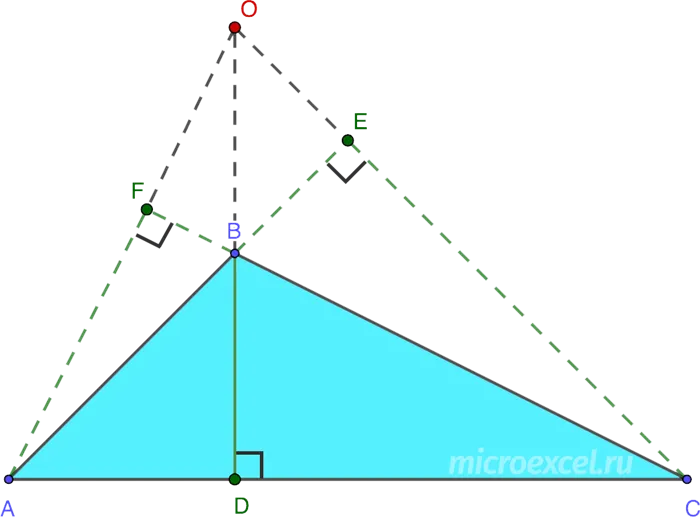
Теорема об ортоцентрической средней точке может быть использована для получения важных свойств высот треугольника, пересекающихся в одной точке. Она формулируется следующим образом: Высоты, нанесенные на любую точку D, пересекаются в точке. Доказательство требует построения произвольного ΔKLM, который не может содержать ни прямого, ни тупого угла. Затем следуйте этому алгоритму:
- Из двух вершин следует провести высоты, которые пересекают противоположную сторону под прямым углом, то есть из вершины L опустить LN на сторону КМ. Аналогичную операцию нужно выполнить для вершины К (KU к LM).
- Высоты пересекутся в некоторой точке — будущем ортоцентре треугольника. Ее следует обозначить W.
- Предположим, что высоты не пересекаются. Следовательно, они параллельны. Это записывается таким образом: LN || KU. Сторона KL является секущей по определению.
- Исходя из третьего пункта, алгебраическая сумма значений углов (∠К/2 и ∠L/2) эквивалентна 180. Из равенства получается, что ∠К + ∠L = 360. Если ∠К и ∠L — внутренние углы ΔKLM, то их сумма не может составлять 360 градусов. Следовательно, предположение ошибочно.
- На основании доказанного в четвертом пункте утверждения можно сделать вывод, что высоты пересекаются в точке W.
- Аналогичным образом доказывается, что высота MV, опущенная из вершины M, проходит через ортоцентр. Для этого нужно повторить 1—5 пункты алгоритма, но вместо KU провести MV.
- Утверждение доказано.
Однако теоремы о высоте недостаточно для решения задач по геометрии. Для этого случая математики вывели полезные свойства и соотношения, которые облегчают нахождение неизвестной величины или доказательство нового утверждения.
Полезные свойства и формулы
При решении задач могут потребоваться определенные свойства ортоцентра, которые были доказаны математиками. К ним относятся следующие:

- Расположение ортоцентра: остроугольный — в центре, прямоугольный — совпадает с образующей прямой угол вершиной, тупоугольный — внешний (находится за пределами треугольника).
- Ортоцентр остроугольного Δ — центр окружности, вписанной в него.
- Алгебраическая сумма квадратов расстояний от вершин до ортоцентра (KW, LW и MW) с учетом квадратов сторон (KL, LM и KM) эквивалентна двенадцати квадратам радиуса окружности R, которая описана вокруг треугольника: KW 2 + LW 2 + MW 2 + KL 2 + LM 2 + KM 2 = 12 * R 2 .
- Расстояние (К) от ортоцентра до середины стороны KL: К = KL / (2 * tg (∠K)). Для других величин (К и К): К = LM / (2 * tg (∠L)) и К = MK / (2 * tg (∠M)) соответственно.
- Величина расстояний от W до вершин (KW, LW и MW): KW = KL / tg (∠K), LW = LM / tg (∠L) и MW = KM / tg (∠M).
- Площадь S: S = KL 2 * sin (∠K) / 2 = LM 2 * sin (∠L) / 2 = KM 2 * sin (∠M) / 2.
Существует определенный класс задач, в которых необходимо определить координаты ортоцентра. В этом случае необходимо нарисовать декартову систему координат и отметить на ней вершины, а затем соединить их отрезками. Затем нужно провести высоты, чтобы найти ортогональный центр треугольника, а затем построить проекции из этой точки на координатные линии.
Поэтому расположение ортоцентра треугольника зависит от его формы и является важным параметром для построения конечной окружности и периметра.
Теорема о пересечении высот треугольника
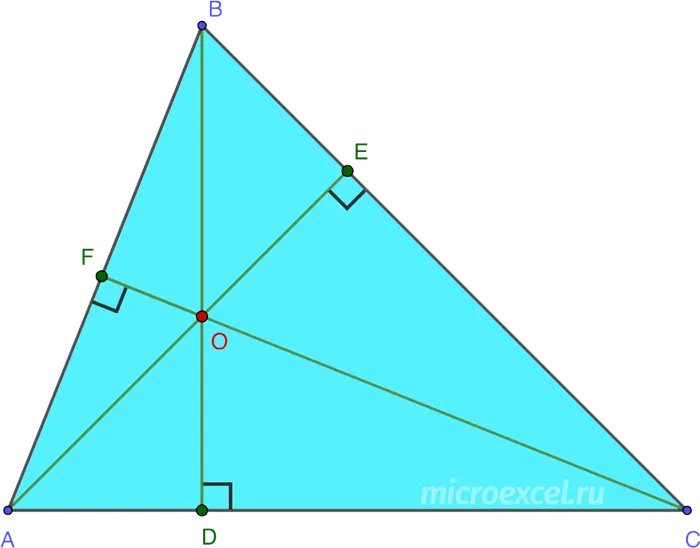
В этом уроке мы узнаем, что высоты (или их продолжения) треугольника пересекаются в точке. Эта точка называется ортоцентром и является еще одной основной точкой треугольника.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам, вам необходимо добавить их в свой личный кабинет.
2. Распространите видеоуроки в своих личных кабинетах среди учеников.
3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Теорема о пересечении высот треугольника»
На сегодняшнем уроке мы продолжим изучать тему диссонирующих точек треугольника и выучим теорему о пересечении высот треугольника.
На предыдущих уроках мы доказали, что биссектрисы треугольника пересекаются в одной точке и что середины перпендикуляров на сторонах треугольника также пересекаются в одной точке. Ранее мы также доказали, что медианы треугольника пересекаются в одной точке. Оказывается, что высоты треугольника обладают тем же свойством.
Теорема. Высоты (или их продолжения) треугольника пересекаются в одной точке.
Доказательство.
Уведомление.
Тогда четырехугольник
Тогда четырехугольник
Средняя точка — это перпендикуляр.
Средняя точка — это перпендикуляр.
Средняя точка — это перпендикуляр.
Поэтому высота составляет .
Что нужно было доказать.
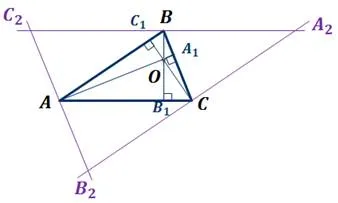
В любом треугольнике медианы и биссектрисы принадлежат самому треугольнику. Что нельзя сказать о высотах треугольника. Три высоты треугольника всегда пересекаются в одной точке. Точка их пересечения называется ортогональным центром треугольника. В остроугольных и правильных треугольниках высоты принадлежат треугольнику. Их точка пересечения, ортоцентр, лежит внутри треугольника в правильном треугольнике и под прямым углом в прямоугольном треугольнике. Однако в тупоугольном треугольнике точка пересечения высот, которая является ортоцентром, лежит вне треугольника.
Рассмотрим тупой угол — obtuse, — основание высоты .
Доказательство.
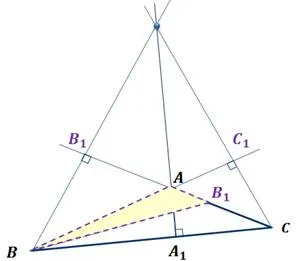
Пусть точка
То, чего не может быть.
Точка пересечения тупоугольного треугольника лежит вне треугольника.
Таким образом, в каждом треугольнике есть четыре точки: пересечение медиан, пересечение биссектрис углов, пересечение срединных перпендикуляров на сторонах треугольника и пересечение высот (или их продолжений). Эти четыре точки называются точками интереса треугольника.
Из истории основных точек треугольника. В четвертой книге «Элементов» Евклид решает задачу: «Вставьте окружность в заданный треугольник». Из решения следует, что три биссектрисы внутренних углов треугольника пересекаются в точке — центре окружности.
Из решения другой евклидовой задачи следует, что перпендикуляры к сторонам треугольника также пересекаются своими серединами в точке, являющейся центром окружности. В «Элементах» не сказано, что три высоты треугольника пересекаются в точке, называемой ортоцентром.
Четвертая точка треугольника является точкой пересечения центров. Архимед доказал, что это центр тяжести треугольника (центроид). Особое внимание было уделено четырем вышеуказанным точкам, и с XVIII века их стали называть «замечательными» или «особыми» точками треугольника.
Изучение свойств треугольника, связанных с этими и другими точками, привело к возникновению новой ветви элементарной математики, «геометрии треугольника» или «новой геометрии треугольника». Леонгард Эйлер был одним из его основателей.








