А именно, отметьте любую точку K на m. Затем проведите через K плоскость β такую, что a||β. Поскольку точки β равноудалены от α, достаточно показать, что m полностью принадлежит β:
Теорема о трех перпендикулярах
Что означает теорема о трех вертикалях в простых терминах?
Как использовать его при проблемах
Использование в ЕГЭ
Давайте начнем с некоторых вводных понятий, разве вы не хотите жить с понятиями?
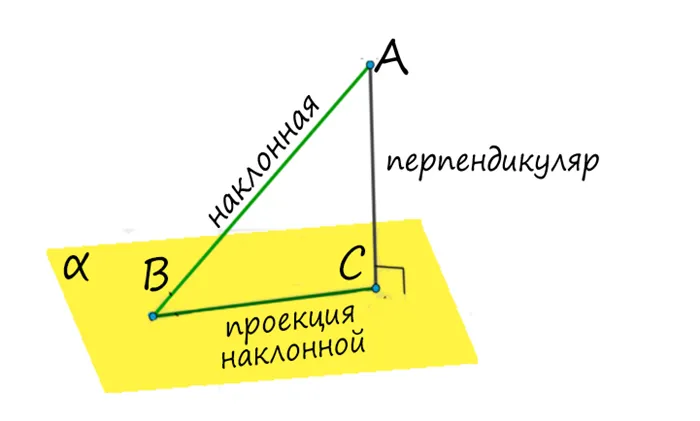
Если через точку B в плоскости альфа провести прямую KL так, чтобы KL ⊥ BC, то по теореме о трех вертикалях (и т.д.) KL ⊥ BA.
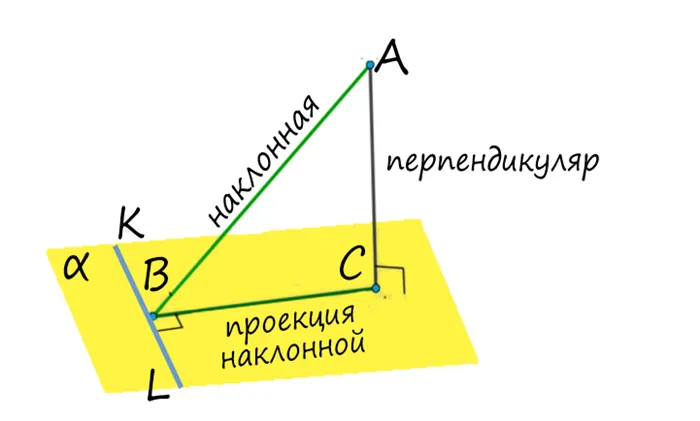
Другими словами, прямая, лежащая в плоскости, перпендикулярна наклону только в том случае, если она перпендикулярна проекции этого наклона на плоскость (обратное также верно).
Давайте рассмотрим самый распространенный пример:
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.
Тетраэдр имеет три пары пересекающихся граней. Мы доказываем перпендикуляр одной пары, остальные делаем по аналогии, например, AD ⊥ BC.
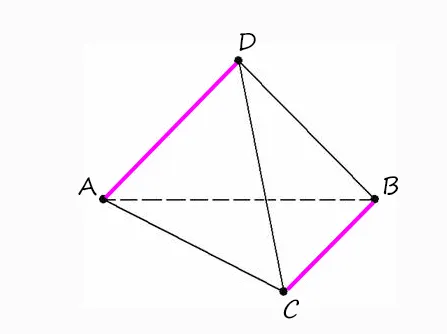
Теперь у нас есть только наклон AD и плоскость (ABC), поэтому нам не хватает проекции наклона и перпендикуляра:
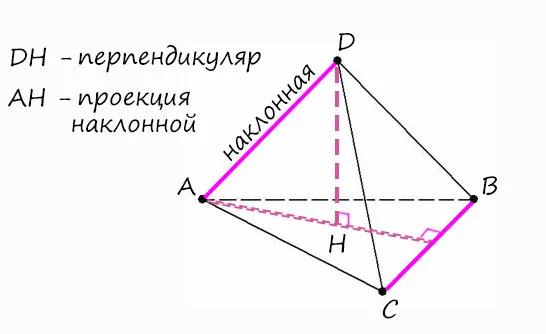
Тогда, чтобы доказать, что AD ⊥ BC: 1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике. 2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) =>DH ⊥ BC.
Доказав это, мы можем с уверенностью сказать, что AD ⊥ BC (всегда должно быть доказательство из двух пунктов и только потом заключение).
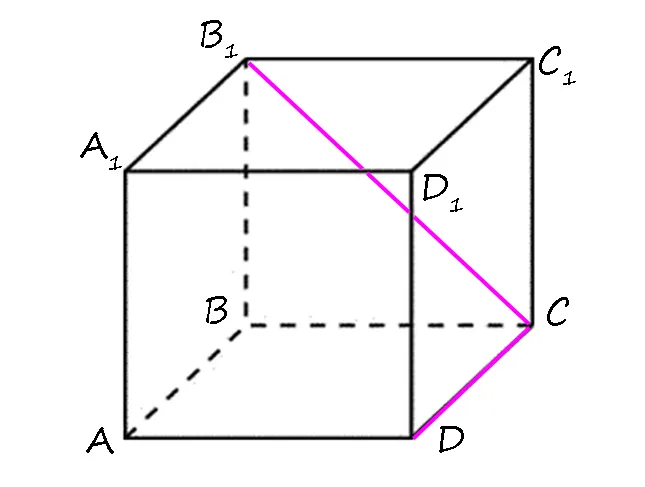
2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.
Если принять B₁C за наклонную плоскость (ABCD), то перпендикуляр равен BB₁, а проекция наклонной плоскости на эту плоскость — BC.
1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) =>BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то она также перпендикулярна всем прямым в этой плоскости). 2) BC ⊥ CD, так как ABCD — прямоугольник. 3) После с.т.: B₁C ⊥ CD.
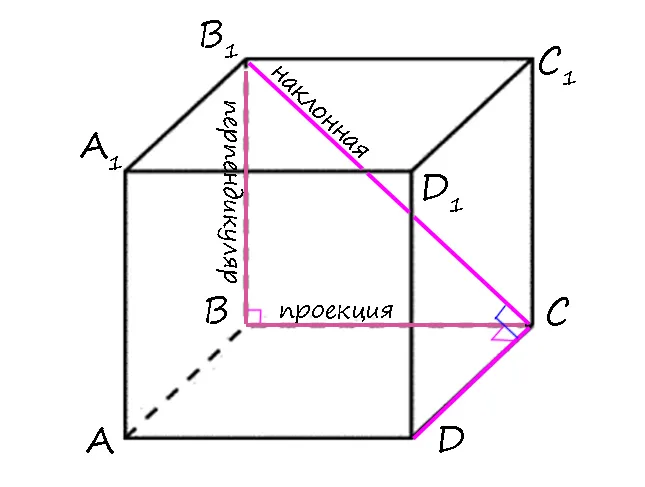
Две точки доказательства, третья точка заключения.
Теорема о трех перпендикулярах
В этой статье мы рассмотрим одну из фундаментальных теорем геометрии, изучаемых в 10-11 классах, — три перпендикуляра. Мы также рассмотрим пример решения задачи для закрепления представленного материала.
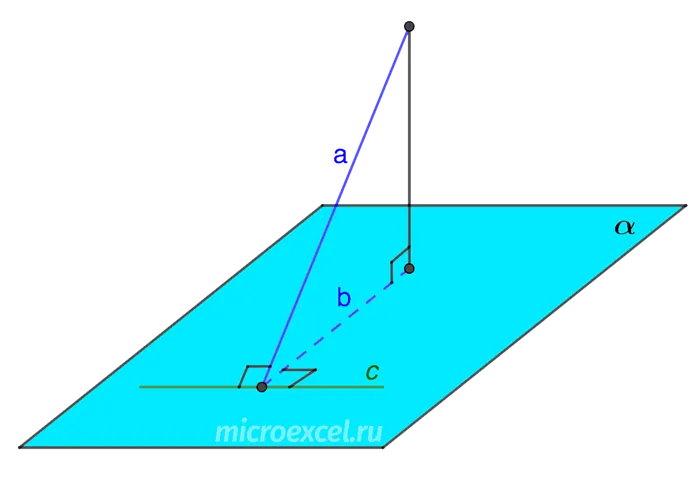
Если провести линию, перпендикулярную проекции склона на плоскость через основание склона, то эта линия также перпендикулярна склону.
- α – плоскость;
- a – наклонная;
- b – проекция наклонной (a) на плоскости ( α );
- с – прямая на плоскости ( α ), перпендикулярная проекции наклонной (b).
Обратная теорема
Если провести перпендикулярную прямую, проходящую через основание склона на плоскости, то эта прямая также перпендикулярна проекции склона на плоскость.
Пример задачи
Длина наклонной, направленной из точки A к плоскости a, равна 10 см, а ее проекция — 6 см. Определите расстояние точки A от плоскости.
Решение Нарисуйте решение задачи в виде следующей диаграммы.
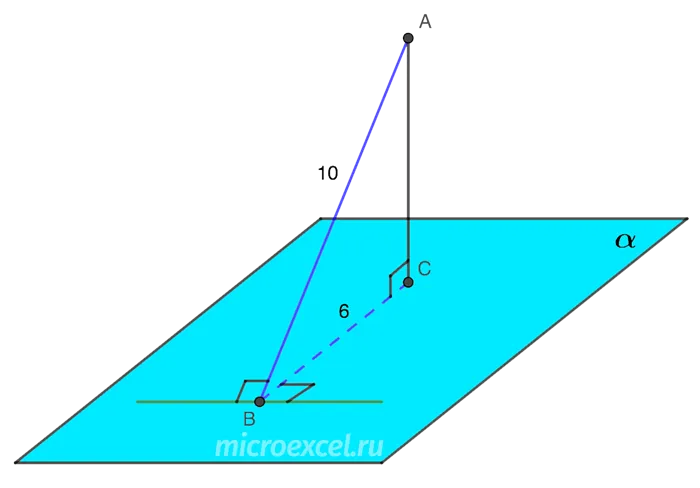
Расстояние A от плоскости α — это длина отрезка AC, который также является образцом правильного треугольника ABC.
Используя теорему Пифагора, получаем:
AC 2 = AB 2 — BC 2 = 10 2 — 6 2 = 64. Следовательно, AC = √ 64 = 8 см.
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра квадрата: формула и задачи
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Теорема косинусов для треугольника: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение площади правильного шестиугольника: формула и примеры
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение площади поверхности цилиндра: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Нахождение радиуса круга: формула и примеры
- Нахождение радиуса цилиндра: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Нахождение площади правильной призмы: формула и задачи
- Нахождение площади правильной пирамиды: формулы
- Формула Герона для треугольника
- Теорема о внешнем угле треугольника: формулировка и задачи
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема Фалеса: формулировка и пример решения задачи
- Геометрическая фигура: треугольник
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Свойства прямоугольного треугольника
- Свойства равнобедренного треугольника: теория и задача
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
Теорема, обратная теореме о трёх перпендикулярах
Если мы заменим термины проекция и наклон, то получим обратное утверждение:
Если линия, проведенная на плоскости через основание склона, перпендикулярна склону, то она также перпендикулярна его проекции.
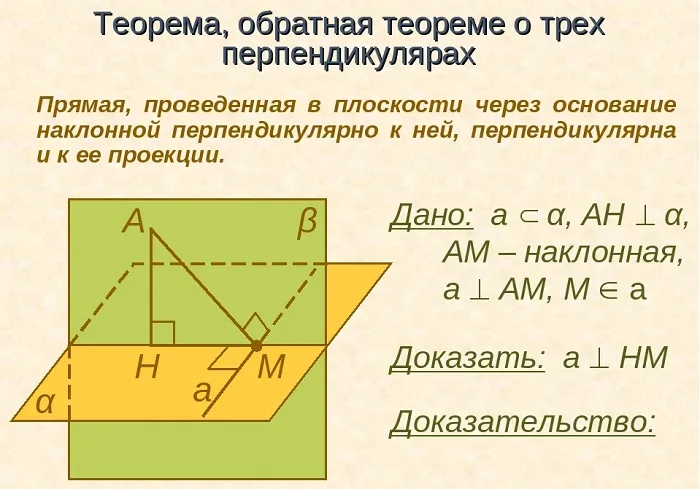
Доказательства аналогичны приведенным ранее.
Решение задач на применение теоремы
Класс задач, в которых используется этот материал, довольно обширен. Многие стереометрические задачи сводятся к поиску прямых углов в изучаемом объекте, так что вопрос о существовании и нахождении неизвестных компонентов переходит в область простых вычислений.
Нет необходимости говорить об уникальности подхода, поскольку любые формулы, правила, свойства могут быть выведены из различных базовых данных и условий.
Задача №1
Докажите, что каждая точка перпендикуляра к плоскости треугольника, проходящего через центр эндоцикла, равноудалена от его сторон.
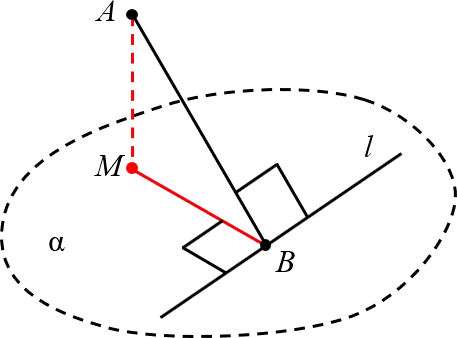
Ситуация со всеми дополнительными конструкциями показана на рисунке.
Каждый из лучей OA, OB, OC образует угол 90º, так как контур касается сторон. Отрезки SA, SB, SC образуют прямые углы со сторонами, а их длины равны требуемым расстояниям.
ΔAOS = ΔBOS = ΔCOS с двумя перпендикулярами (SO — общий, OA = OB = OC = r), поэтому SA = SB = SC.
Задача №2
Основание пирамиды MABCD — прямоугольник со сторонами 6 и 8. Высота MB равна 2. MB перпендикулярна плоскости прямоугольника ABCD.
Найдите расстояние точки M от диагонали CA и длину ребра MD.
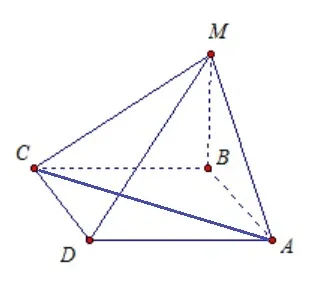
Ответ на первый вопрос требует знания определения расстояния. Это длина перпендикуляра, проведенного из данной точки к прямой.
Пусть MH — требуемое расстояние. Тогда MH ⊥ AC.
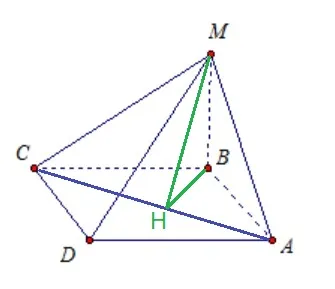
Согласно второму утверждению, BH ⊥ AC.
Поскольку ΔABC прямоугольный, BH можно вычислить как высоту по формуле:
Рассчитать переменный ток несложно:
![]()
![]()
Так как диагонали прямоугольника имеют одинаковую длину, найдите MD:








