Теорема Менелая. Теорема менелая для треугольника.

Содержание

Если на сторонах AB и BG треугольника ABC точки C₁и А₁и точка B₁лежит на продолжении стороны AB за точку C, тогда точки C₁, А₁и Б₁находятся на одной прямой тогда и только тогда, когда выполнено равенство: $\frac>B>\times \frac>C>\times \frac>A>=1$

Теорема Менелая

Теорема Менелая показывает соотношение сторон треугольника, которое получается, когда линия пересекает две стороны треугольника и продолжение третьей.

Используя эту теорему, можно найти соотношение сторон треугольника и доказать прилипание точек в данном треугольнике (на двух сторонах и продолжении третьей стороны).

Концентрические точки — это три или более точек на одной прямой.

Теорема Менелая гласит:

BD/DC * CE/EA * AF/FB = 1

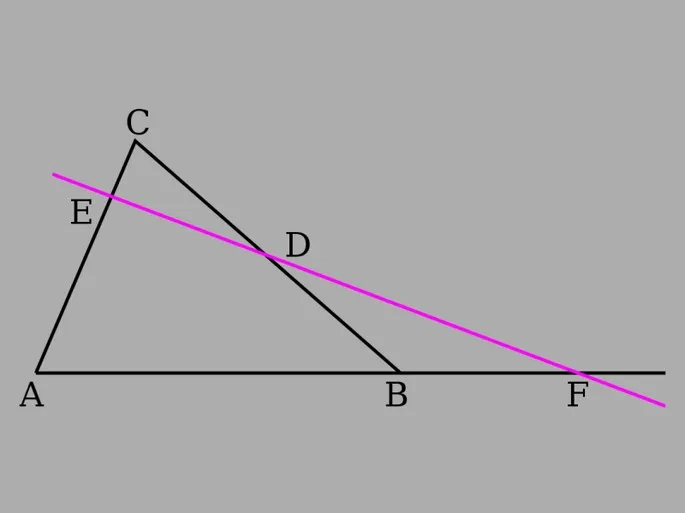
Шаг 1 Дан треугольник ABC. Линия пересекает две стороны треугольника таким образом, что не проходит через вершину треугольника (на нашем рисунке это розовая линия). Таким образом, есть два пересечения прямой с двумя сторонами треугольника (точки E и D). Третья сторона (AB) должна достичь точки пересечения (точка F).

Шаг 2. Возьмите вершину треугольника и перейдите в другую точку треугольника, пройдя точку пересечения (затем разделите одно на другое): BD/DC.

Обратите внимание, что в этой нотации пересечение находится в середине («DD»), а B и C (стороны треугольника, по которым мы идем) — по бокам. То есть, мы идем от B к C через D. Мы можем написать точки на стороне, по которой мы идем («BC»), с небольшим пробелом между ними, а затем вставить пересечение между ними дважды со знаком дроби («D/D»).

При входе во фракцию точка, через которую мы проходим, повторяется по диагонали.

Отметьте на рисунке карандашными стрелками, какую сторону мы уже прошли, а какую нам еще предстоит пройти, чтобы не запутаться.

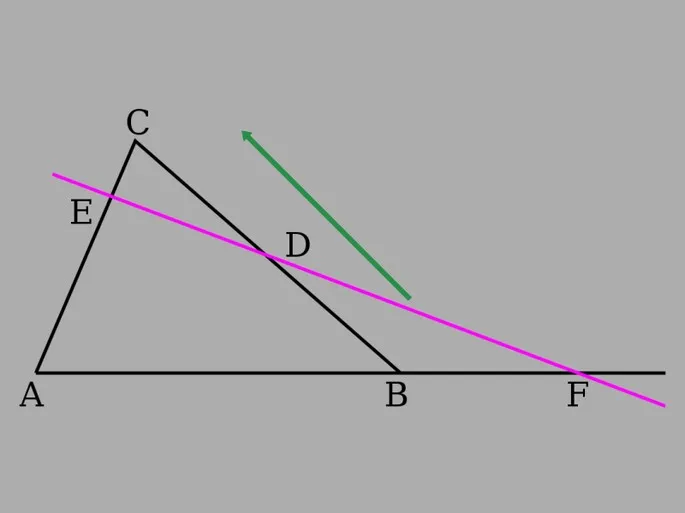
Шаг 3. Продолжите движение вдоль треугольника и сделайте сторону CA — это похоже на движение от C к E к A, что получается CE/EA.

Перемножьте эти две стороны и запишите их вместе в тетрадь:

Шаг 4. Теперь проведем сторону AB через точку F — от A пройдем сначала к F, а затем обратно к B, получится вот так: АФ/ФБ.

Шаг 5. Перемножьте все вместе:

BD/DC * CE/EA * AF/FB

Теорема Менелая гласит:

BD/DC * CE/EA * AF/FB = 1

Доказательство теоремы Менелая

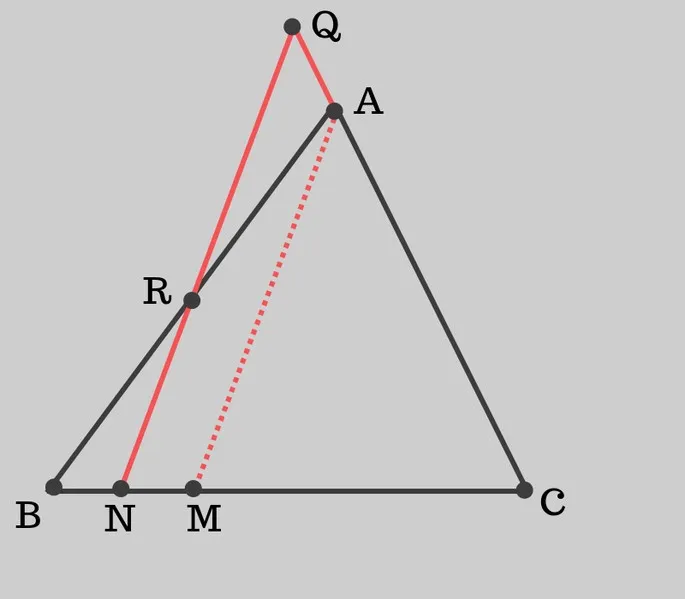
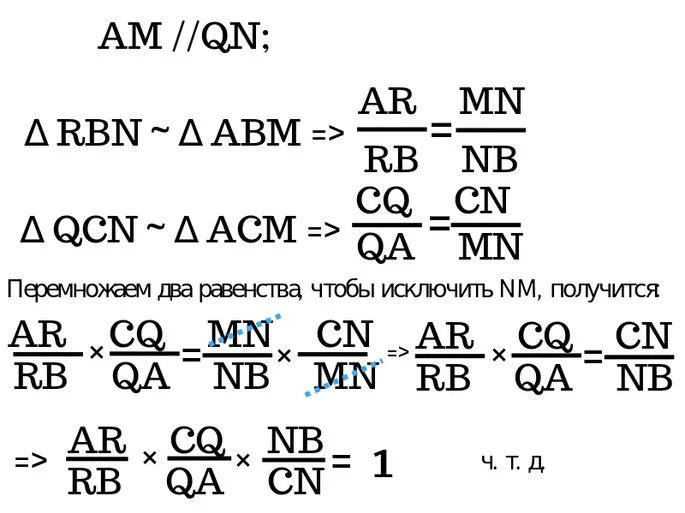
Существует много способов доказать эту теорему, этот способ называется «доказательство с помощью подобных треугольников»:

Проведите прямую, параллельную QN через точку A и пересекающую сторону BC в точке M.

Теорема Менелая пример (задача с решением)

Существует треугольник ABC. На стороне BC существует точка L такая, что LC = 3BL. Точка A соединяется с продолжением стороны AC, на которой лежит точка M, так что MA = AC. Прямая ML пересекает AB в точке F.

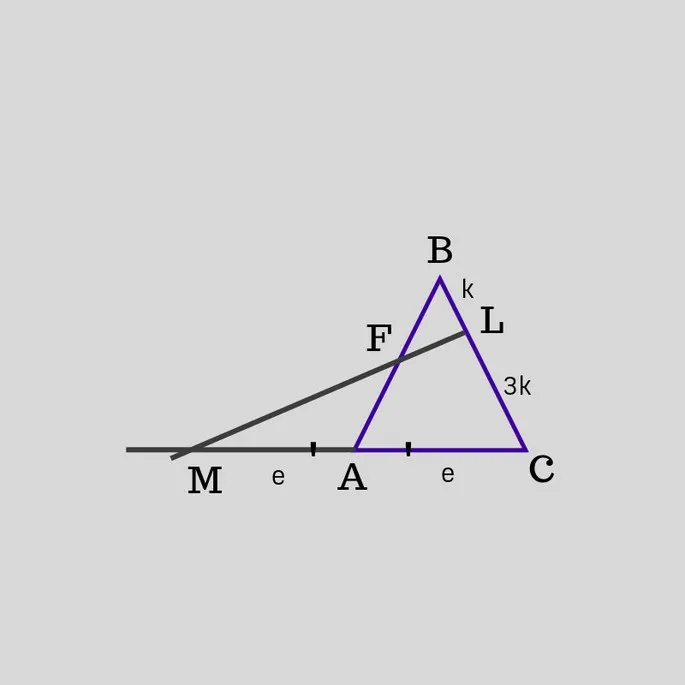
Найдите отношение BF/FA:

1. мы знаем, что MA = AC, LC = 3BL.

2. прямая ML пересекает две стороны треугольника ABC и является продолжением третьей стороны, т.е. по теореме Менелая:

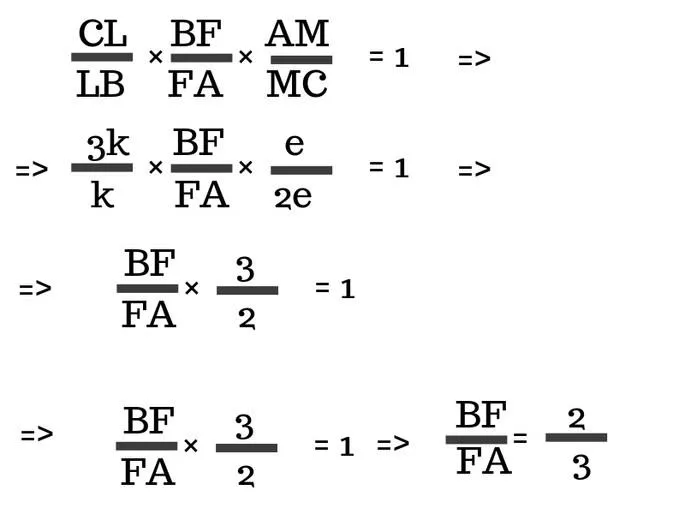
1 Формулировка теоремы Менелая

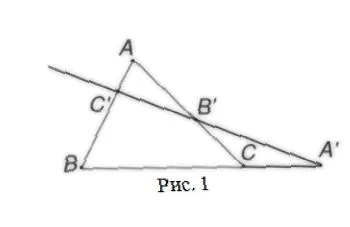
Линия пересекает треугольник $ABC$, при этом $C’$ пересекается со стороной $AB$, $B’$ пересекается со стороной $AC$, а $A’$ пересекается с продолжением стороны $BC$ (рисунок 1). Тогда отношения таковы:

$ \bigg (\frac \bigg ) \cdot \bigg ( \frac \bigg ) \cdot \bigg ( \frac \bigg ) = 1$

Доказательство теоремы Менелая очень простое. Например, один из обычных способов доказательства требует лишь одного дополнительного построения. Проведите прямую, параллельную $AB$, через вершину $C$ и используйте две получившиеся пары подобных треугольников. Недавно я записал видео с доказательством:

Обратная теорема Менелая также верна.

2 Как запоминать теорему Менелая

Возьмите любой угол треугольника и, начиная с него, обведите стороны треугольника. Каждый раз после вершины вы должны достичь точки разделения (точка, промежуточная точка). То есть, если направление и порядок пересечения таковы, что вы попадаете из вершины $A$ в вершину $C$, то из точки $C$ вы сначала попадаете в точку $A’$, а из точки $A’$ — в точку $B$. Напишите на каждой стороне отношение, которое учитывает выбранное вами направление. Произведение трех результирующих коэффициентов равно единице.

В 1678 году итальянский инженер Джованни Чева доказал следующую теорему.

Определение. Отрезки, соединяющие вершины треугольника с точками на противоположных сторонах (или их продолжения), называются шевронами, если они пересекаются в одной точке.

Возможны два варианта расположения цевиантов: в одном варианте точка пересечения находится внутри, а концы цевиантов — на сторонах треугольника. Во втором варианте точка пересечения находится снаружи, конец одного цевиана лежит на одной стороне, а концы двух других цевианов лежат на продолжениях сторон (см. рисунки).

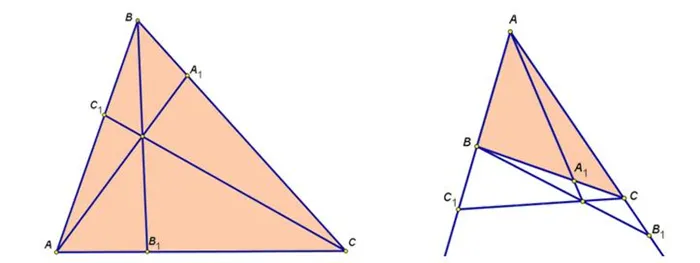
Прямая теорема Чевы.

Если в любом треугольнике $ABC$, $CA$, $AB$ или их продолжениях взять точки $A_$, $B_$ и $C_$ соответственно так, чтобы прямые $AA_$, $BB_$, $CC_$ пересекались в общей точке, то

$ \bigg (\frac>\bigg ) \cdot \bigg ( \frac\bigg ) \cdot \bigg ( \frac{) = 1$

Я не привожу доказательство, оно основано на двойном применении теоремы Менелауста.

Также применима обратная теорема Чевы.

4 Как запоминать теорему Чевы

Внимательно запомните теорему Менелая — выберите вершину в качестве начальной точки и направления пересечения. Дальше мы делаем все точно так же, как в формулировке теоремы Менелая.

Теоремы Менелая и Чевы не нужно запоминать, но вы должны запомнить принцип и ситуации, к которым они применимы. Заучивание самих отношений с точной символикой — занятие не только неблагодарное, но и вредное. В моей статье с видео о соотношениях разрезов вы найдете примеры задач с теоремой Менелая — некоторые из них решены, другие предназначены для упражнений.

Теорема Менелая: формулировка и пример с решением

В этом посте мы рассмотрим одну из классических теорем общей геометрии — теорему Менелая, названную в честь древнегреческого математика и астронома Менелая Александрийского. Мы также рассмотрим пример решения задачи для закрепления представленного материала.

Даны треугольник ABC и прямая, проходящая через треугольник следующим образом:

B’ – точка пересечения со стороной AC ;

C’ – точка пересечения со стороной AB ;

A’ – точка пересечения прямой и продолжения стороны ВC;

Важно: A’, B’ и С’ лежат на одной прямой, т.е. являются коллинеарными.

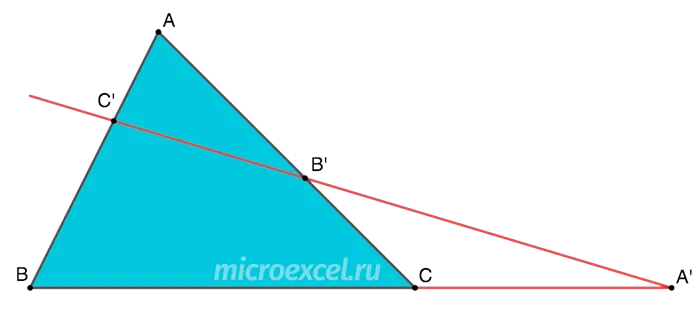
Если все вышеперечисленные условия выполнены, то соотношение длин отрезков верно:

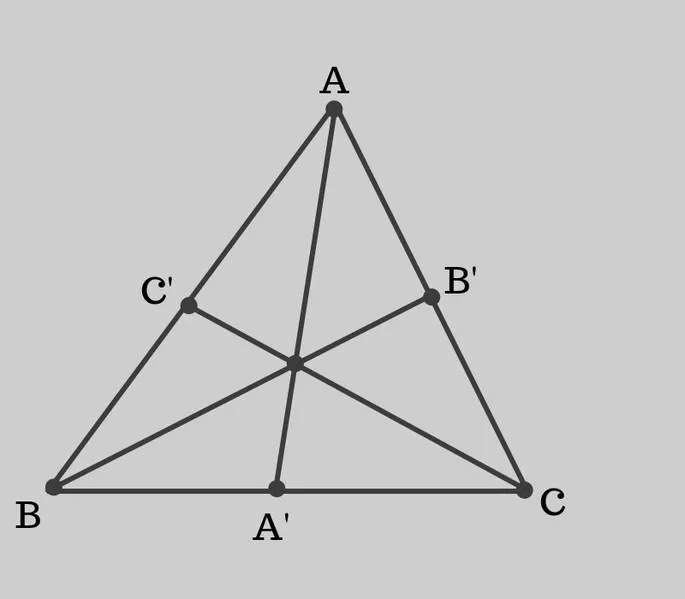
Следствия из теоремы

1. тригонометрический эквивалент.

Примечание: Все углы выровнены.

2.

Пример задачи

3. вид теоремы в геометрии Лобачевского

Дан треугольник ABC с точками X на стороне AB и Y на стороне AC. Точка Z возникает на пересечении прямых, проходящих через эти точки, и продолжения BC. BC вдвое длиннее CZ, а отрезки AY и YC имеют одинаковую длину. Найдите отношение BX к XA.

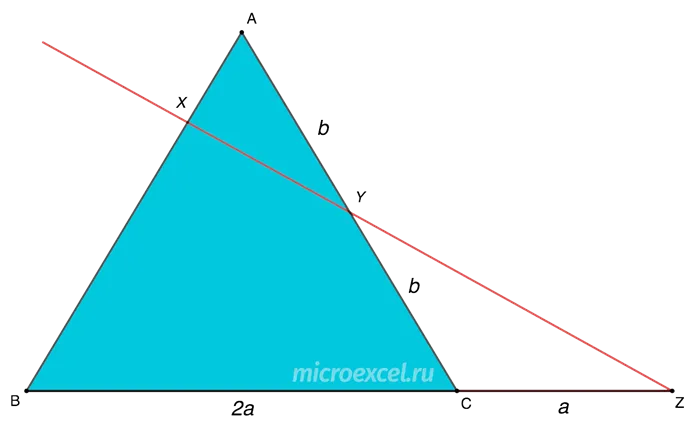
Представим условия задачи в виде диаграммы. Для простоты обозначим отрезок CZ через a (т.е. BC = 2a ), а AY=YC через b .

Теперь определите отношение отрезков, используя теорему Менелая:

Замените заданные отрезки нашими обозначениями:

После сокращения дробей получаем:

Публикации по теме:

Нахождение площади квадрата: формула и примеры

Нахождение площади прямоугольника: формула и пример

Нахождение площади круга: формула и примеры

Нахождение площади ромба: формула и примеры

Нахождение площади трапеции: формула и примеры

Нахождение площади параллелограмма: формула и примеры

Нахождение площади эллипса: формула и пример

Нахождение площади выпуклого четырехугольника: формула и пример

Нахождение периметра треугольника: формула и задачи

Нахождение периметра прямоугольника: формула и задачи

Нахождение периметра ромба: формула и задачи

Нахождение периметра трапеции: формула и задачи

Нахождение периметра параллелограмма: формула и задачи

Нахождение длины окружности: формула и задачи

Теорема Пифагора для прямоугольного треугольника: формула и задачи

Теорема синусов для треугольника: формула и задачи

Теорема о сумме углов треугольника: формула и задачи

Тригонометрические функции острого угла в прямоугольном треугольнике

Нахождение объема конуса: формула и задачи

Нахождение объема цилиндра: формула и задачи

Нахождение объема куба: формула и задачи

Нахождение объема шара: формула и задачи

Нахождение объема пирамиды: формула и задачи

Нахождение площади правильного шестиугольника: формула и примеры

Нахождение объема тетраэдра: формула и задачи

Нахождение объема призмы: формула и задачи

Нахождение объема параллелепипеда: формула и задачи

Нахождение площади поверхности куба: формула и задачи

Нахождение площади поверхности цилиндра: формула и задачи

Нахождение площади поверхности конуса: формула и задачи

Нахождение площади поверхности шара (сферы): формула и задачи

Нахождение радиуса шара: формула и примеры

Нахождение радиуса круга: формула и примеры

Нахождение радиуса цилиндра: формула и примеры

Нахождение площади прямоугольного параллелепипеда: формула и пример

Нахождение площади правильной призмы: формула и задачи

Нахождение площади правильной пирамиды: формулы

Формула Герона для треугольника

Теорема о внешнем угле треугольника: формулировка и задачи

Теорема Чевы: формулировка и пример с решением

Теорема Стюарта: формулировка и пример с решением

Теорема о трех перпендикулярах

Теорема Фалеса: формулировка и пример решения задачи

Геометрическая фигура: треугольник

Признаки равенства треугольников

Признаки подобия треугольников

Свойства равнобедренного треугольника: теория и задача

Свойства равностороннего треугольника: теория и пример задачи

Определение и свойства медианы треугольника

Определение и свойства медианы прямоугольного треугольника

Применение теорем Чевы и Менелая при решении задач ЕГЭ

Следовательно, BX = 3XA .

Задача 1

Теорема Менелая (как и обратная ей) применима к первой части теста и к задаче 16. Рассмотрим пару таких задач.

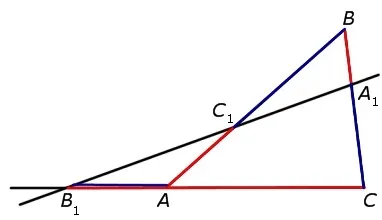
Пусть дан треугольник ABC (см. рисунок ниже) с продолжением стороны CA. Существуют также диаметры BM и AN, пересечение которых мы обозначим через O.

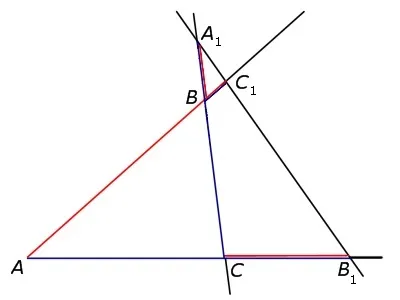
Постройте точку K на стороне AB так, чтобы AK составляла 1/3 от AB. AC = 4 см, AM = 2 см. Начертите OK в точке пересечения с AC. Обозначим точку пересечения с P. Обозначим AP через y. Найти: Каково расстояние AP. Решение.

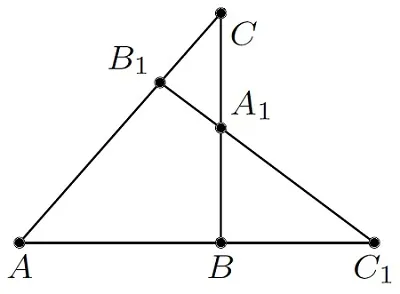
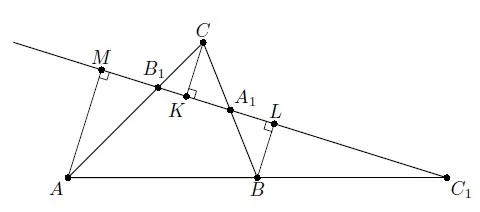
Рассмотрим треугольник ABM. Для этого треугольника возьмем линию OP. Таким образом, мы находим искомые точки P, A, M, O, K и B. Запишем теорему Менелая для этого рисунка.

Задача 2

Из этого следует, что y = 4. Ответ: отрезок AP = 4 см.

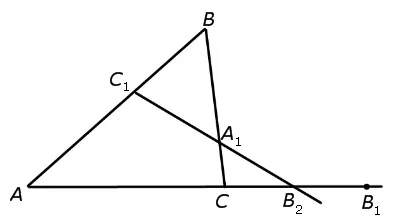
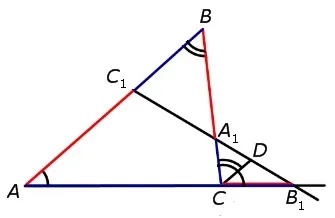
Проблема, связанная со свойствами теоремы Чевы. Рассмотрим рисунок:

Найдите: отношение BO и OB1.

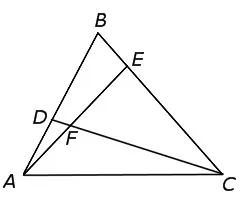
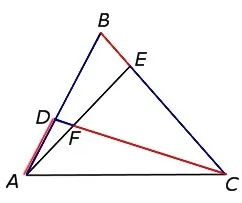
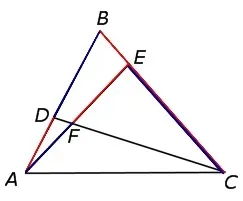
Поэтому давайте запишем отношение: