γ 2 — α 2 = β ( β + 2 α из-за ( π — γ ) ) = b ( b — 2 a из-за γ ), c ^ -a ^ &<>= b (b + 2acos (p i-gamma)) &<>= b (b-2acos gamma), конец>>
Теорема косинусов для треугольника: формула и задачи
В этой статье мы рассмотрим одну из фундаментальных теорем евклидовой геометрии, теорему косинусов, которая определяет отношение сторон треугольника, а также научимся применять ее на практике для решения задач.
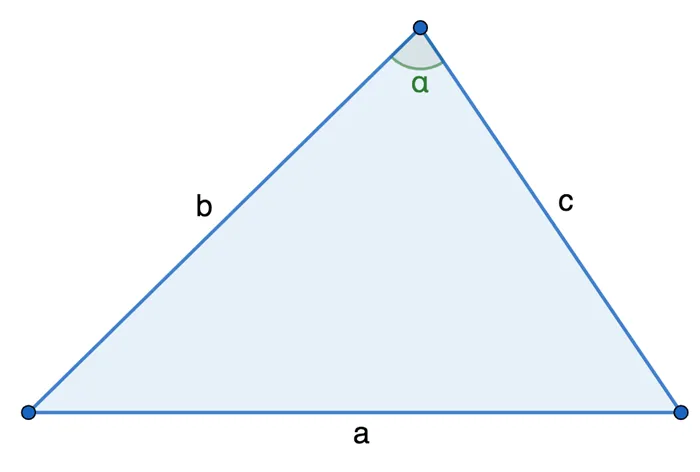
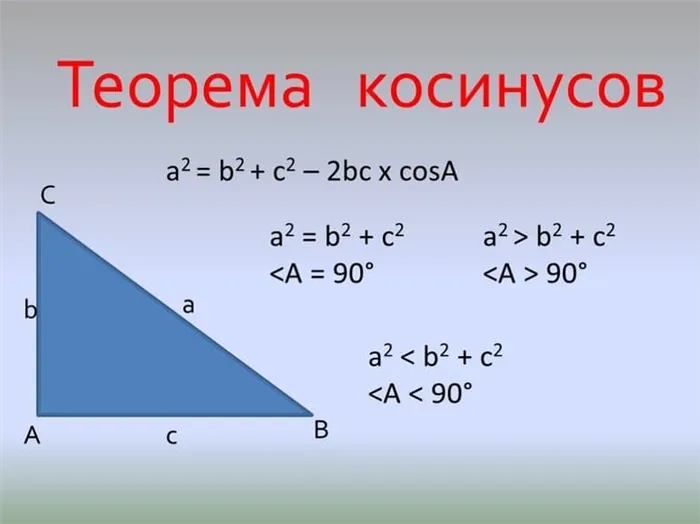
В плоском треугольнике квадрат одной стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла между ними.
a 2 = b 2 + c 2 — 2 ⋅ b ⋅ c ⋅ cos a
Следствие из теоремы
Формулу теоремы можно применить для нахождения косинуса угла в треугольнике:
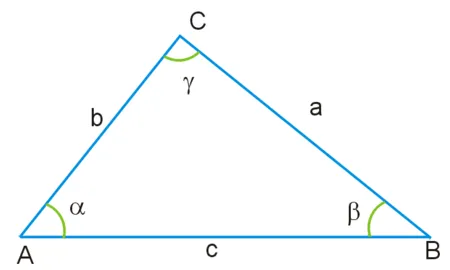
В данном случае:
- если b 2 + c 2 – a 2>0, значит угол α – острый;
- если b 2 + c 2 – a 2 = 0, значит угол α равен 90 градусам (терема косинусов принимает вид Теоремы Пифагора);
- если b 2 + c 2 – a 2<0, значит угол α – тупой.
Примеры задач
Задача 1 В треугольнике известны длины двух сторон, 5 и 9 см, а угол между ними равен 60°. Найдите длину третьей стороны.
Решение: применим формулу теоремы, обозначив известные стороны как b и c, а неизвестную сторону как a: a 2 = 5 2 + 9 2 — 2 ⋅ 5 ⋅ 9 ⋅ cos 60° = 25 + 81 — 45 = 61 см2 .
Задача 2 Самая длинная сторона треугольника равна 26 см, а две другие стороны — 16 и 18 см. Найдите угол между меньшими сторонами.
Решение: Примем большую сторону за. Чтобы найти угол между b и c, воспользуйтесь следствием теоремы:

Следовательно, угол a = arccos (-1/6) ≈ 99,59°.
Публикации по теме:
- Нахождение площади квадрата: формула и примеры
- Нахождение площади прямоугольника: формула и пример
- Нахождение площади треугольника: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение площади выпуклого четырехугольника: формула и пример
- Нахождение периметра параллелограмма: формула и задачи
- Нахождение длины окружности: формула и задачи
- Теорема Пифагора для прямоугольного треугольника: формула и задачи
- Тригонометрические функции острого угла в прямоугольном треугольнике
- Нахождение объема конуса: формула и задачи
- Нахождение объема тетраэдра: формула и задачи
- Нахождение объема призмы: формула и задачи
- Нахождение площади поверхности конуса: формула и задачи
- Нахождение площади поверхности шара (сферы): формула и задачи
- Нахождение площади поверхности вписанного в цилиндр шара
- Теорема Чевы: формулировка и пример с решением
- Теорема Стюарта: формулировка и пример с решением
- Теорема о трех перпендикулярах
- Признаки равенства треугольников
- Признаки подобия треугольников
- Признаки равенства прямоугольных треугольников
- Определение и свойства медианы треугольника
- Определение и свойства медианы прямоугольного треугольника
- Определение и свойства медианы в равнобедренном треугольнике
- Свойства биссектрисы равностороннего треугольника
- Нахождение радиуса вписанной в треугольник окружности
- Что такое квадрат: определение и свойства
- Нахождение радиуса вписанной в квадрат окружности
- Что такое прямоугольник: определение, свойства, признаки, формулы
- Нахождение площади сектора круга
- Нахождение длины дуги сектора круга
- Нахождение высоты трапеции: формулы и примеры задач
- Нахождение высоты равнобедренной (равнобокой) трапеции
- Нахождение высоты прямоугольной трапеции
- Что такое средняя линия четырехугольника
- Нахождение радиуса описанной вокруг куба сферы (шара)
- Нахождение радиуса вписанного в куб шара
- Нахождение площади шарового сектора
- Нахождение объема шарового сектора
- Нахождение площади шарового слоя
- Нахождение объема усеченного конуса
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Что такое пирамида: определение, элементы, виды, варианты сечения
- Что такое призма: определение, элементы, виды, варианты сечения
- Основные свойства призмы
- Нахождение радиуса вписанного в цилиндр шара (сферы)
- Нахождение радиуса шара (сферы), вписанного в правильную пирамиду
- Нахождение радиуса сферы (шара), описанной около правильной пирамиды
- Что такое правильный многоугольник: определение, признаки, элементы, виды
- Что такое ломанная: определение, обозначение, элементы, виды, пример задачи
Доказательство теоремы косинусов
Таким образом, теорема косинусов применима к любому треугольнику (с острыми и тупыми углами, даже к прямому треугольнику!).
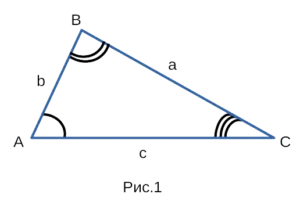
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
Рассмотрим три случая:
- угол С острый,
- угол С тупой,
- угол С прямой.
И убедитесь, что теорема косинусов применима ко всем трем случаям!
Угол С острый
Проведите высоту \( \displaystyle AH\) из точки \( \displaystyle A\) и рассмотрите треугольник \( \displaystyle AHB\).
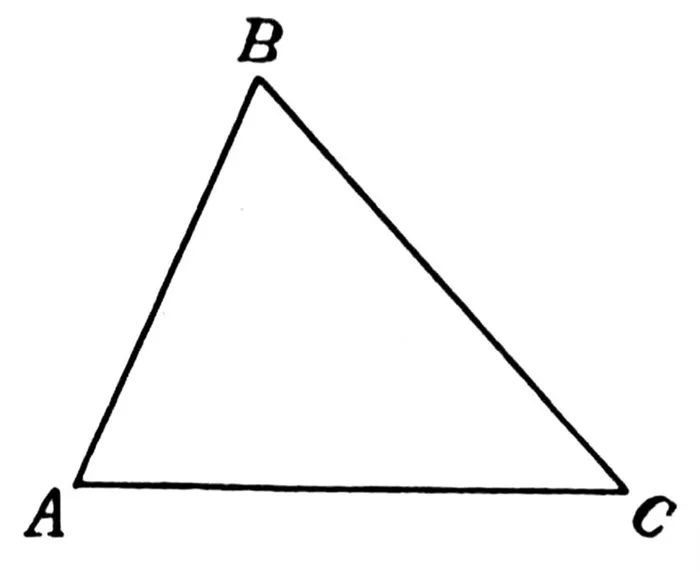
Она прямоугольная, можно применить теорему Пифагора:
Что такое \( \displaystyle AH\) и \( \displaystyle HB\)?
\( \displaystyle AH\) может быть выражен треугольником (прямоугольником!) \( \displaystyle AHC\).
\( \displaystyle AH=b\sin \gamma\).
А вот \( \displaystyle BH=a-CH=a-b\cos \gamma\) (снова из \( \displaystyle \Delta AHC\) ).
Открыть ответы…
Чтобы открыть все задачи учебника с синей полосой (как эта), вам нужно один раз зарегистрироваться:
Угол С тупой
Начните таким же образом: Опустите высоту от точки \displaystyle A\.

Теперь обратите внимание на разницу!
\( \displaystyle AH=b\sin \left( ^>-\гамма \права)\) происходит от \( \displaystyle \Delta AHC\), которая теперь находится вне \( \displaystyle \Delta ABC\), и
\( \displaystyle BH=a+b\cos \left( ^>-\{\gamma
Открыть ответы…
ight)\).
Угол С прямой
Мы постоянно работаем над улучшением этого учебника, и вы можете нам помочь. Доступ и неограниченное использование пособия «Юклава» (100+ статей по всем темам ЕГЭ и ОГЭ, 2000+ решенных заданий, 20+ вебинаров — практических занятий).
В каких же задачах бывает полезна теорема косинусов?
Но тогда \( \displaystyle \cos \gamma =0\) и теорема косинусов просто превращается в теорему Пифагора:
Например, если у вас есть две стороны треугольника и угол между ними, вы можете сразу же найти третью сторону.
Если у вас есть все три стороны, вы можете определить косинус любого угла по формуле:
И даже если у вас есть две стороны и угол НЕ между ними, вы можете найти третью сторону, решив квадратное уравнение. В этом случае, однако, вы иногда получаете два ответа и должны решить, какой из них выбрать или оставить оба.
Попробуйте и не бойтесь — теорема косинусов почти так же проста в применении, как теорема Пифагора.
Бонус: Вебинар на решение задач по теореме косинусов и синусов
И присоединяйтесь к бесплатным вебинарам и курсам (см. ниже).
Теорема косинусов (и теорема синусов) является универсальным инструментом для решения треугольников — это теорема косинусов и теорема синусов.
А как мы уже знаем, почти все задачи по планетометрии связаны с треугольниками.
Данный вебинар является частью курса подготовки к ЕГЭ по математике (см. ниже). Вы изучите сами теоремы и узнаете, как применять их при решении задач части 1.
История
Возьмите ручку и бумагу и решайте их вместе с Алексеем Шевчуком.
Теоремы, обобщающие теорему Пифагора и соответствующие теореме косинусов, были сформулированы отдельно для острых и тупых углов во второй книге Евклида в теоремах 12 и 13.
В работах среднеазиатских математиков утверждения, соответствующие теореме косинуса, были применены к сферическому треугольнику. Теорема косинусов для сферического треугольника в ее обычной форме была сформулирована Региомоданом, который назвал ее «теоремой Альматегни» (в честь аль-Баттани).
Вариации и обобщения
- Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трехгранного угла.
- Теоремы косинусов (геометрия Лобачевского)
Четырёхугольник
Возводя в квадрат тождество +\overline+\overline» width=»» height=»» />В Европе теорема косинусов стала известна благодаря Франсуа Вье в XVI веке. В начале 19 века его стали записывать в алгебраической нотации, которая используется и по сей день.
Можно сделать утверждение, которое иногда называют теоремой косинусов для четырехугольников:
Симплекс
((n-1)!)^2>\begin 0 & 1 & 1 & 1 & \dots & 1 \\ 1 & 0 & d_^2 & d_^2 & \dots & d_^2 \\ 1 & d_^2 & 0 & d_^2 & \dots & d_^2 \\ 1 & d_^2 & d_^2 & 0 & \dots & d_^2 \\ \vdots&\vdots&\vdots & \vdots & \ddots& \vdots \\ 1 & d_^2 & d_^2 & d_^2 & \dots & 0 \\ \end» width=»» height=»» />
— Угол между прямыми AB и CD .
A — угол между гранями, » width=»» height=»» />В этом случае мы должны удалить строку и столбец, где или .
См. также
- Решение треугольников
- Скалярное произведение
- Соотношение Бретшнайдера
- Теорема косинусов для трехгранного угла
- Сферическая теорема косинусов
- Теорема котангенсов
- Теорема синусов
- Теорема тангенсов
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М .: МЦНМО, 2004. — С. 84-85. — ISBN 5-94057-170-0
- Теоремы
- Геометрия треугольника
- Тригонометрия
Пример решения задачи
— расстояние между вершинами i и j.

Мы знаем, что длина сторон треугольника равна 6 см, 8 см и 10 см. Необходимо определить площадь этой фигуры.
Для решения задачи можно воспользоваться ресурсами Интернета, где есть множество сайтов, на которых с помощью онлайн-калькуляторов можно найти нужное значение по известным данным. Однако интересно решить эту задачу с помощью теоремы косинусов.
Площадь любого треугольника можно вычислить следующим образом:
Где h — высота, построенная в точке a. Известные стороны a = 6 см, b = 8 см, c = 10 см. Чтобы найти высоту h, сначала вычислите угол между a и c. Для этого можно использовать косинус. Для этой цели можно использовать закон косинуса:
b = arccos ((a 2 + c 2 — b 2 )/(2*a*c)) = arccos ((6 2 + 10 2 — 8 2 )/(2*6*10)) = 53,13°.
Если мы теперь посмотрим на треугольник, образованный высотой h, стороной c и частью стороны a, то увидим, что это правильный треугольник (c — гипотенуза). В этом случае h можно найти по синусу угла b:
h = c*sin (β) = 10* sin (53,13°) = 8 см.
Длина высоты h равна длине стороны b. Это означает, что исходный треугольник был правильным (вы можете проверить это с помощью теоремы Пифагора). Его площадь составляет:
S = ½*a*e = ½*a*b = ½*6*8 = 24 см 2 .
Аналог для тетраэдров
Аналогичное утверждение начинается с того, что α, β, γ, δ быть площадями четырех граней тетраэдр. Обозначим двугранные углы к β γ ^>>Таким образом, теорема косинусов является универсальным инструментом для решения геометрических задач с треугольниками. С его помощью можно найти все остальные характеристики фигуры, включая ее площадь, используя три известных параметра.
α 2 = β 2 + γ 2 + δ 2 − 2 β γ потому что ( β γ ^ ) + γ δ потому что ( γ δ ^ ) + δ β потому что ( δ β ^ ). = eta ^ + gamma ^ + delta ^ -2left eta gamma cos left (>ight) + gamma delta cos left (>ight) + delta eta cos left (>ight) ight.>
Версия для малых углов
и т.д. Затем 6
c 2 = ( а − б ) 2 + 4 а б грех 2 ( γ 2 ) = ( а − б ) 2 + 4 а б Хаверсин ( γ ). c ^ & = (ab) ^ + 4absin ^ left (>ight) & = (ab) ^ + 4aboperatorname (гамма) .end>>
Когда угол γ меньше, а смежные стороны α и β имеют одинаковую длину, правая часть стандартной формы закона косинуса может потерять большую часть своей численной точности. В случаях, когда это важно, может оказаться полезной математически эквивалентная версия закона косинуса, например, формула Хаверсина:
В сферической и гиперболической геометрии
В предельном случае бесконечно малого угла закон косинуса вырождается в длину дуги круговой формулы γ = a γ .
Сферический треугольник решается по закону косинуса.
потому что а = потому что б потому что c + грех б грех c потому что А потому что А = − потому что B потому что C + грех B грех C потому что а. cos a & = cos bcos c + sin bsin ccos A cos A & = — cos Bcos C + sin Bsin Ccos a.end>>
Аналоги закона косинуса для евклидовой плоскости также применимы к единичной сфере и гиперболической плоскости. В сферической геометрии треугольник определяется тремя точками you, v и w на единичной сфере и дугами большой окружности, соединяющими эти точки. Если эти большие окружности образуют углы A, B и C с противоположными сторонами a, b и c, то закон сферического косинуса утверждает, что оба следующих соотношения выполняются:
шиш a = шиш b шиш c — sin b sin c потому что A
где син и ши — гиперболические синус и косинус, а второй — гиперболические синус и косинус
потому что A = — потому что B потому что C + sin B sin C шиш а .








