Теорема Фалеса: формулировка и пример решения задачи. Теорема фалеса 8 класс.

Содержание

Фалес из Милета был когда-то главным основателем ионийской школы. Бесценным капиталом этого человека стало создание многофункциональной научной геометрии. Великий ученый, владевший специфически египетским искусством измерения, смог собственными усилиями создать индуктивную геометрию, полезную для человечества.

Теорема Фалеса: формулировка и пример решения задачи

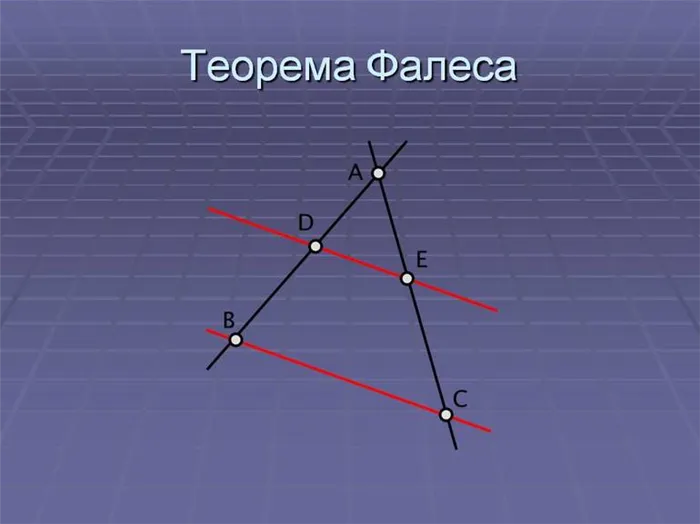
В этой статье мы рассмотрим одну из фундаментальных теорем геометрии 8-го порядка — теорему Фалеса, названную в честь греческого математика и философа Фалеса Милетского. Мы также рассмотрим пример решения задачи для закрепления представленного материала.

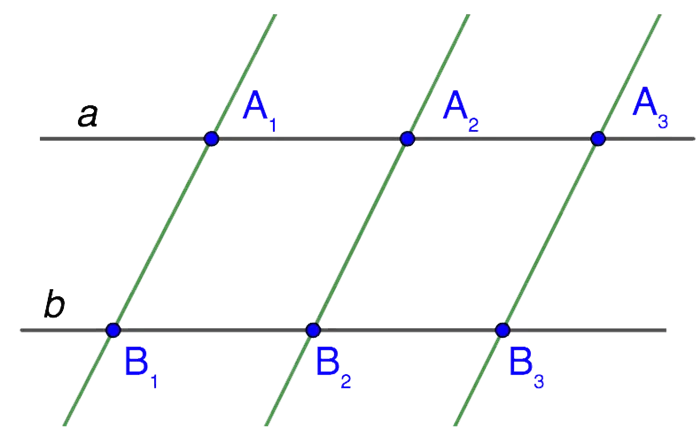
Если отложить равные отрезки на одной из двух прямых и провести от их концов параллельные прямые, то они пересекут вторую прямую и пересекут равные отрезки на ней.

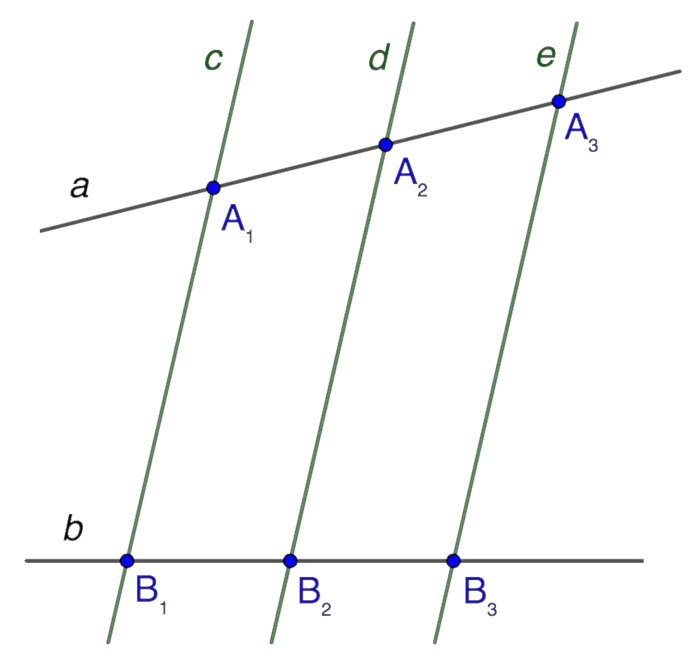
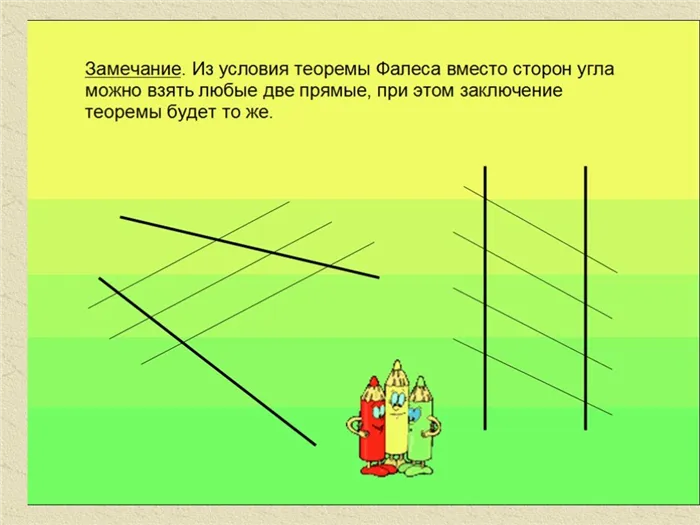
Примечание: Взаимное пересечение вторых прямых не имеет значения, то есть теорема применима как к пересекающимся, так и к параллельным прямым. Положение сегментов на отрезках прямой также не имеет значения.

Обобщенная формулировка

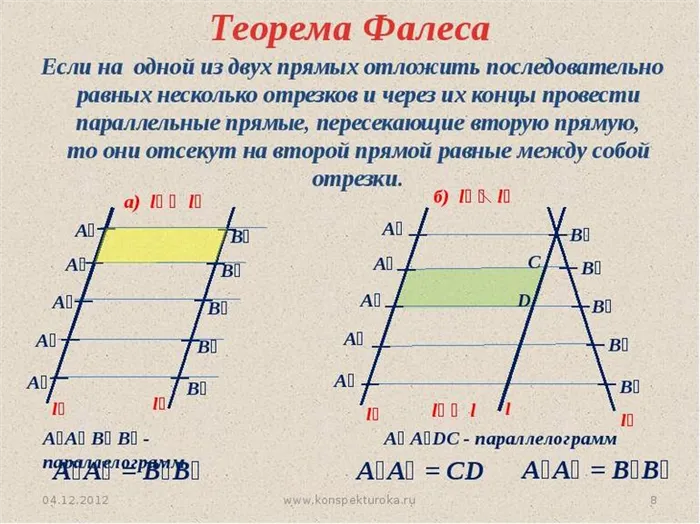
Теорема Фалеса является частным случаем теоремы пропорциональности*: Параллельные линии разрезают пропорциональные отрезки на второстепенные.

Следовательно, для нашего рисунка выше имеет место следующее равенство:

*, поскольку отрезки равны, т.е. являются аналогами с коэффициентом пропорциональности, равным единице.

Обратная теорема Фалеса

1. для пересечения сегментов

Если прямые пересекают две другие прямые (параллельные или нет) и делят их на равные или пропорциональные отрезки, начиная от вершины, то эти прямые параллельны.

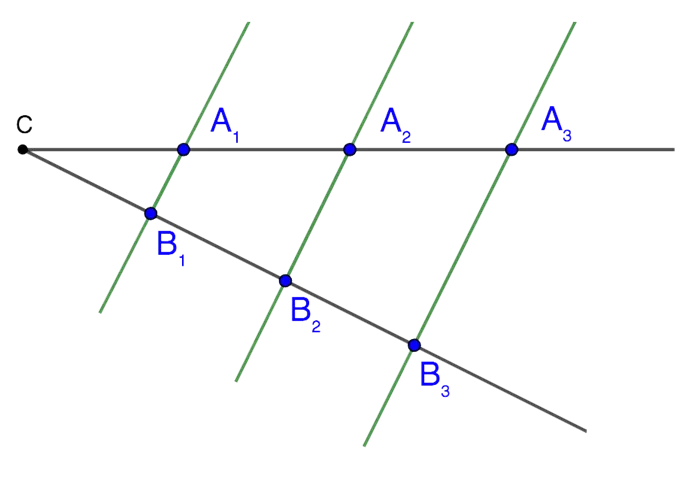
Это следует из теоремы об обратном:

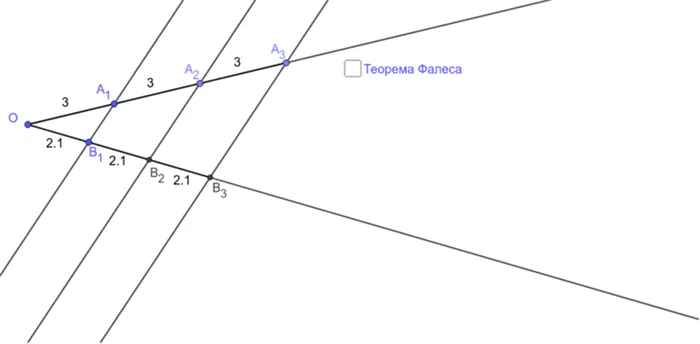
Обязательное условие: равные отрезки должны начинаться из вершины.

2. для параллельных вторичных линий

Отрезки двух вторичных линий должны быть равны. Только в этом случае теорема применима.

Пример задачи

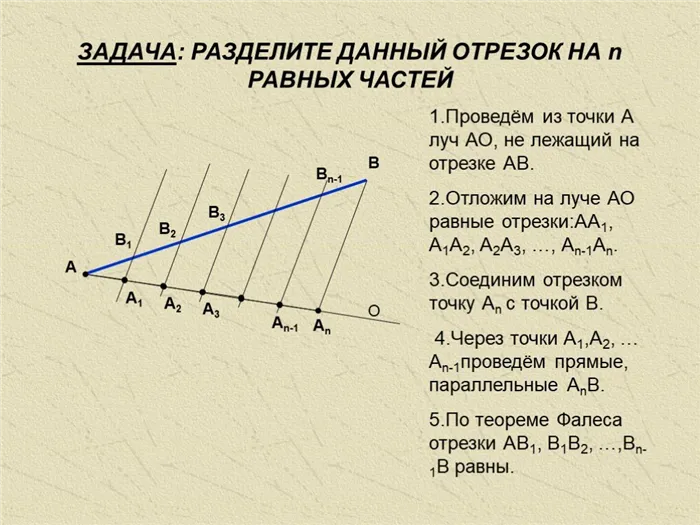
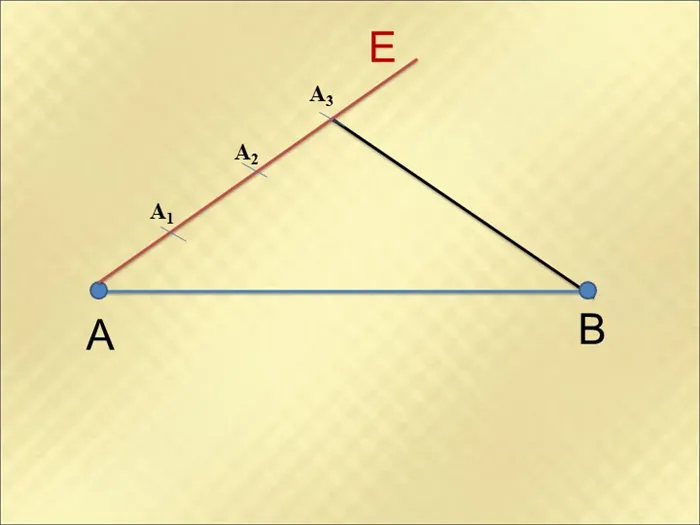
Пусть дан отрезок AB на плоскости. Разделите его на 3 равные части.

Решение

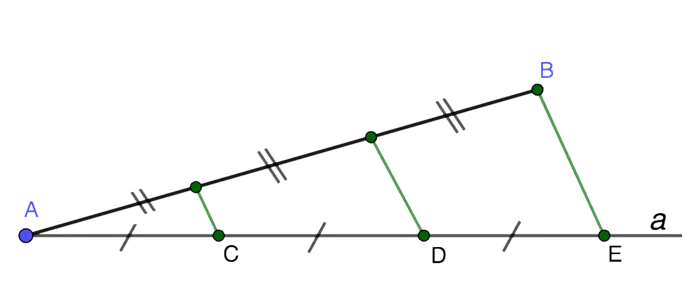
Проведите прямую a из точки A и отметьте на ней три последовательные равные части AC, CD и DE.

Соедините конечную точку E прямой a с точкой B отрезка. Затем через оставшиеся точки C и D проведите две прямые, которые параллельны BE и пересекают отрезок AB.

Пересечения, образованные таким образом в отрезке AB, делят его на три равные части (по теореме Фалеса).

Публикации по теме:

Нахождение площади квадрата: формула и примеры
Нахождение площади прямоугольника: формула и пример
Нахождение площади треугольника: формула и примеры
Нахождение площади круга: формула и примеры
Нахождение площади ромба: формула и примеры
Нахождение площади параллелограмма: формула и примеры
Нахождение площади эллипса: формула и пример
Нахождение площади выпуклого четырехугольника: формула и пример
Нахождение периметра квадрата: формула и задачи
Нахождение периметра треугольника: формула и задачи
Нахождение периметра прямоугольника: формула и задачи
Нахождение периметра трапеции: формула и задачи
Нахождение периметра параллелограмма: формула и задачи
Нахождение длины окружности: формула и задачи
Теорема Пифагора для прямоугольного треугольника: формула и задачи
Теорема косинусов для треугольника: формула и задачи
Теорема синусов для треугольника: формула и задачи
Теорема о сумме углов треугольника: формула и задачи
Тригонометрические функции острого угла в прямоугольном треугольнике
Нахождение объема конуса: формула и задачи
Нахождение объема цилиндра: формула и задачи
Нахождение объема куба: формула и задачи
Нахождение объема пирамиды: формула и задачи
Нахождение площади правильного шестиугольника: формула и примеры
Нахождение объема тетраэдра: формула и задачи
Нахождение объема призмы: формула и задачи
Нахождение объема параллелепипеда: формула и задачи
Нахождение площади поверхности куба: формула и задачи
Нахождение площади поверхности цилиндра: формула и задачи
Нахождение площади поверхности конуса: формула и задачи
Нахождение площади поверхности шара (сферы): формула и задачи
Нахождение площади поверхности вписанного в цилиндр шара
Нахождение радиуса круга: формула и примеры
Нахождение радиуса цилиндра: формула и примеры
Нахождение площади прямоугольного параллелепипеда: формула и пример
Нахождение площади правильной призмы: формула и задачи
Нахождение площади правильной пирамиды: формулы
Формула Герона для треугольника
Теорема о внешнем угле треугольника: формулировка и задачи
Теорема Чевы: формулировка и пример с решением
Теорема Стюарта: формулировка и пример с решением
Теорема о трех перпендикулярах
Геометрическая фигура: треугольник
Признаки равенства треугольников
Признаки подобия треугольников
Признаки равенства прямоугольных треугольников
Свойства прямоугольного треугольника
Свойства равнобедренного треугольника: теория и задача
Определение и свойства медианы треугольника
Определение и свойства медианы прямоугольного треугольника

Краткое описание

Фалес известен в истории как одаренный геометр. Этому человеку многие ученые приписывают открытие и доказательство многих теорий. Фалесу удалось разработать очень интересный метод определения точного расстояния между берегом и плавучим средством, видимым невооруженным глазом. Некоторые историки склонны считать, что ученый использовал для этой цели точку определенного подобия правильных треугольников. Современные последователи великого математика ценят в нем то, что он смог вывести и доказать множество теорем и законов.

Именно греки дали наиболее логичное доказательство правильности гипотез, основанных на единых теоремах, которые считаются установленными истинами. Сегодня историкам трудно сказать, что именно принадлежит Фалесу в научном каталоге. Благодаря этому талантливому человеку Греция приобрела не только философа и математика, но и естествоиспытателя.

Перед изучением теоремы важно понять, что параллелограмм — это правильный четырехугольник, у которого все противоположные стороны попарно параллельны. Однако трапеция — это особый четырехугольник, у которого две стороны параллельны, а две другие стороны имеют противоположные свойства. Изучение этого предмета состоит из нескольких частей, так как сначала необходимо ознакомиться с теорией и только потом можно приступать к решению задач.

Основные понятия

Фалес доказал, что две прямые RF и NS называются параллельными, только если они лежат в одной плоскости и не пересекают друг друга, независимо от их длины. Это правило всегда обозначается как RF || NS.

В любом случае, все существующие точки данной линии располагаются на неизменном расстоянии от второй линии. Это означает, что все прямые, параллельные одной прямой, также параллельны друг другу. Математики считают, что суммарный угол между параллельными прямыми равен 0. Однако это утверждение верно только в том случае, если отрезки имеют одинаковое направление и смещены на 180 градусов.

В качестве наглядного примера можно рассмотреть случай, когда перпендикуляры RF, NS, EF принадлежат одной прямой PE и параллельны друг другу. Линия PE перпендикулярна всем остальным линиям. Общая длина вертикального отрезка, образованного между двумя параллельными прямыми, равна расстоянию между средними линиями. При рассмотрении пространственной теоремы необходимо понимать, что восемь углов образуются в результате пересечения двух параллельных прямых с третьей прямой.

Приведенная специалистами формулировка теоремы Фалеса содержит множество нюансов, которые обязательно должен знать любой человек, желающий решать различные математические задачи. Иначе было бы трудно избежать наиболее распространенных ошибок. Даже кратко изложенная теория позволяет понять наиболее важные математические тонкости. Чтобы ученику было понятно, как именно применять теорему, можно использовать специальные таблицы, расширяющие итоговые математические навыки ученика.

Научное пояснение значений

Если по очереди попытаться разместить несколько равных отрезков только на одной из двух линий, а затем провести прямые линии через конечные точки, которые могут пересечь вторую линию, то равные отрезки можно отсечь на второй линии. Расширенной формулировкой этой теоремы в геометрии является теорема о пропорциональном геометрическом сечении. В качестве наглядного примера ознакомьтесь с формулой: S 1S2/N 1V2 = S 2S3/N 2N3 = S 1S3/N 1N3 .

Важные нюансы:

Востребованная теорема греческого математика является частным случаем закона о пропорциональных отрезках, так как идентичные отрезки можно считать пропорциональными с элементарным коэффициентом ровности, который равняется единице.
В изучаемой теореме нет каких-либо ограничений и требований на взаимное расположение всех секущих. Это связано с тем, что она верна как для пересекающихся прямых, так и для параллельных линий. На итоговый результат совершенно не влияет то, где находятся отрезки на секущих.

Для того чтобы изучить все нюансы этой темы, необходимо рассмотреть вариант, демонстрирующий ситуацию с несоединенными парами сегментов. Например: существующий угол пересекает прямые LL1 || BB1 || CC1 || KK1 и LB = CK. Через L и C проводится прямая, параллельная другой стороне образованного угла LB2B1L1 и CK2K1C1. Свойства параллелограмма также имеют свои особенности:

Треугольники? JSS2 и ? CCC2 равны. Они построены на основе второго принципа равенства геометрических фигур. Если целью задачи является безусловное доказательство параллельности прямых, то нам необходимо выполнить несколько простых действий. Необходимо провести линию SC. Углы SCK и JSC равны как внутренние пересечения под прямыми SC и JS и под вторичной SC. Однако углы JCS и CSK равны как внутренние пересечения параллельных прямых JC и SK, вторичных по отношению к SC. Согласно второму признаку равенства треугольников, геометрические фигуры JSC и KCS, следовательно, равны. Отсюда следует, что JC = SK и JS = SC.

Теорема Фалеса

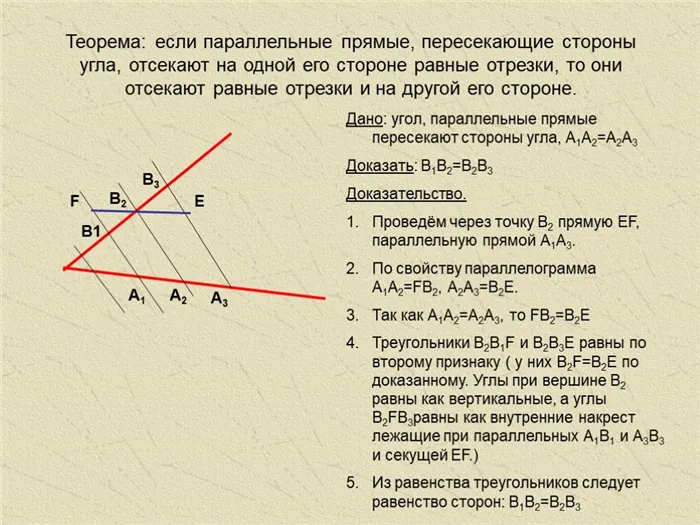
Теорема Фалеса — это теорема о пропорциональных отрезках: Если параллельные прямые отсекают равные отрезки от одной стороны угла, то они также отсекают равные отрезки от другой стороны угла.

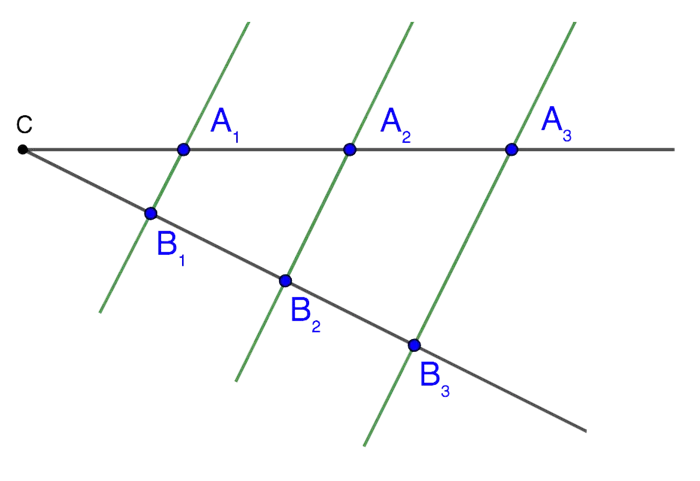
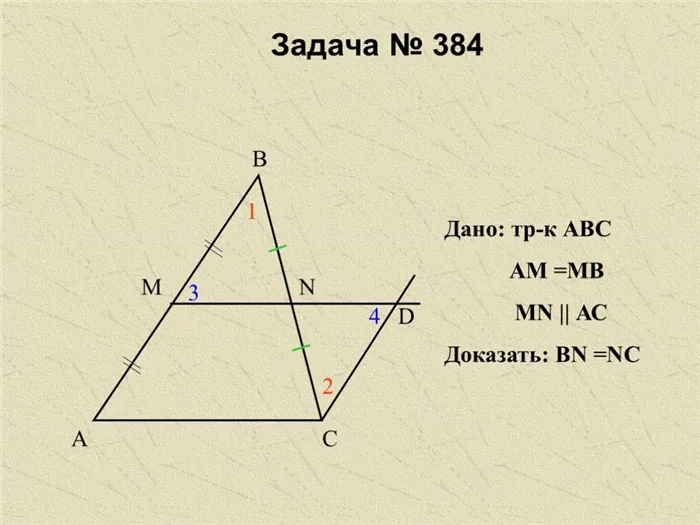
Рассмотрите угол ABC и докажите, что три прямые A₁C₁, A₂C₂, A₃C₃которые параллельны друг другу, одновременно отрезают равные части от своих сторон BA и BC. Предположим, что A₁C₁, A₂C₂, A₃C₃пересекают стороны данного угла. Тогда отрезки A₁A₂и А₂A₃равны друг другу. Докажите, что отрезки C₁С₂и C₂С₃которые получаются в результате пересечения BC, также равны.

Итак, проведем две линии C₁М и С₂N параллельно стороне BA. Линия C₁M пересекает прямую A₂C₂в точке L. После построения прямых получаем два четырехугольника, A₁A₂LC₁и А₂A₃NC₂. Очевидно, что они являются параллелограммами, так что сторона C₁L равно A .₁A₂, С₂N равно A .₂A₃. Из этого следует, что C₁L равно C .₂N.

Кроме того, углы C₁LC₂, LMN и C₂NC₃также согласуются с параллельными линиями. Аналогично, равенство углов LC₁C₂и NC₂C₃. Поэтому треугольник C₁LC₂равен треугольнику C₂NC₃на стороне BC и на двух смежных углах LC₁C₂и NC₂C₃. Таким образом, отрезки C₁C₂и C₂С₃равны как стороны равных треугольников. Это должно быть доказано.

Следствие из теоремы Фалеса

Наиболее важным следствием теоремы Фалеса является теорема о пропорциональных отрезках: Две параллельные прямые, пересекающие одну сторону угла, пересекают пропорциональные отрезки его сторон.

Рассмотрим угол ABC и две параллельные прямые A₁C₁и А₂C₂которые пересекают стороны BA и BC. Утверждение верно, если мы докажем, что B A₁/ BA₂= BC₁/ BC₂. Предположим, что это равенство не выполняется и что BA₁/BA₁меньше, чем BC₁/BC₂. Это означает, что BC₁меньше, чем (BA₁∙ BC₂)/BA₂. В Британской Колумбии₂BE = (BA₁∙ BC₂)/BA₂. E находится между B и C₁потому что BE меньше, чем BC.₁.

Для натурального числа n разделите часть BC₂на n равных частей. Предположим, что длина отрезка равна y, так что BC₂= ny. Постройте прямые, параллельные A₂C₂проведите линии через концы этих отрезков. Согласно теореме Фалеса, эти линии рассекают отрезок BA₂на n равных отрезков. Примите x за длину каждого отрезка. Поэтому BA₂= nx.

Если в пределах сегмента EC₁является большим числом n, то существуют точки, составляющие отрезок BC₂. Если в качестве одной из этих точек взять M, то BM = my. Прямая, принадлежащая этой точке, пересекает точку BA₂в L. Тогда BL = mx.

Отсюда следует, что BM / BC₂= my / ny = m / n = mx / nx = BL / BA .₂. Однако БЭ1тогда BE/BC₂2= BL/BC₂1/BA₂. Поэтому BE<( BA₁∙ BC₂)/ BA₂что противоположно BE = ( BA₁∙ BC₂)/ BA₂. Поэтому полученное противоречие является доказательством теоремы о пропорциональной части.

Применение теоремы Фалеса

В качестве примера применения теоремы Фалеса рассмотрим задачу. По договоренности предоставляется участок MN. Его необходимо разделить на три равные части. Сначала проведите прямую m из точки M. Отметьте на этой линии три последовательных отрезка ME, EC и CD. Затем соедините точку D с точкой N, проведите прямые, параллельные DN, через точки E и C, аналогичные этим точкам. Они пересекаются с отрезком MN. Таким образом, пересечение, образованное MN, делит отрезок MN на три равные части.

В следующей задаче дан параллелограмм ABCD. Необходимо доказать, что AE = EO = OC. Согласно свойству параллелограмма, стороны AB и CD равны и параллельны друг другу. Проведите диагональ AC и две параллельные прямые из вершин B и D к серединам противоположных сторон. BN пересекает AC в точке O, а DM пересекает AC в точке E. Две точки обозначены как BN и DM.

Согласно свойству параллелограмма, стороны AB и CD равны и параллельны друг другу. Тогда MB = ½ AB = ½ CD = ND. Это означает, что MB и ND параллельны друг другу. Благодаря этому признаку, MBND является параллелограммом, а согласно свойству параллелограмма, DM параллелен BN.

Рассмотрим AB и AO, вторичные ME и BO. Поскольку AM = MB, то по теореме Фалеса AE = EO. Затем рассмотрим AC и CD, вторичные NO и DE, согласно теореме Фалеса, CN = ND, EO = OC. Исходя из уже доказанных уравнений, AE = EO = OC. Это должно быть доказано.

Научное пояснение значений

Важные нюансы:

Востребованная теорема греческого математика является частным случаем закона о пропорциональных отрезках, так как идентичные отрезки можно считать пропорциональными с элементарным коэффициентом ровности, который равняется единице.
В изучаемой теореме нет каких-либо ограничений и требований на взаимное расположение всех секущих. Это связано с тем, что она верна как для пересекающихся прямых, так и для параллельных линий. На итоговый результат совершенно не влияет то, где находятся отрезки на секущих.

Ключевые особенности теоремы

Если ученик попытается начертить различные отрезки на одной из двух прямых, а затем провести параллельные прямые от их концов, пересекающие вторую прямую, то в итоге он получит одинаковые отрезки на второй прямой. Даже в школьной математике часто используется обобщенная теорема Фалеса: Линии, образованные только параллельными прямыми на одной прямой, пропорциональны другой прямой.

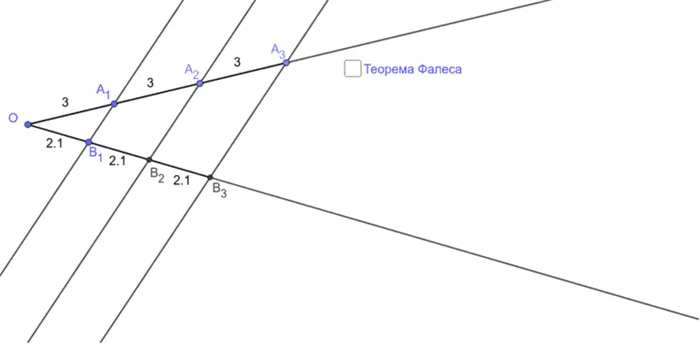
Записи об идеях Фалеса не сохранились до наших дней, поэтому историкам приходится восстанавливать информацию из различных источников. Специалисты доказали, что греческий математик установил 7 теорем по геометрии. Основное правило гласит, что если параллельные прямые, по которым пересекаются стороны угла, пересекают равные части только на одной стороне угла, то аналогичная ситуация возникает и на другой стороне угла.

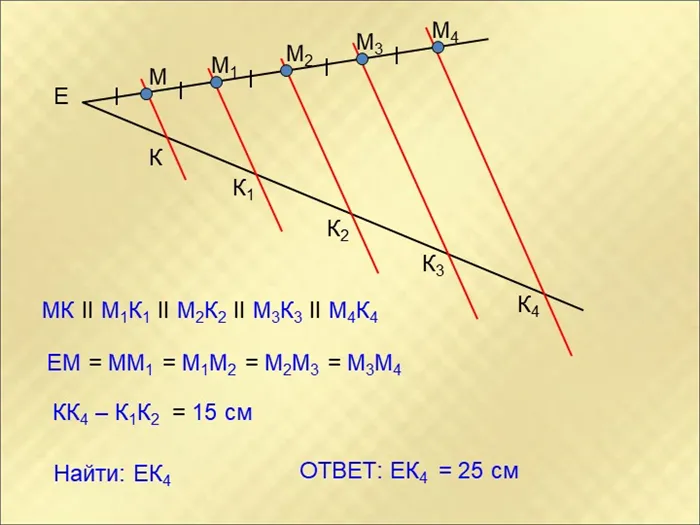
Наглядное доказательство

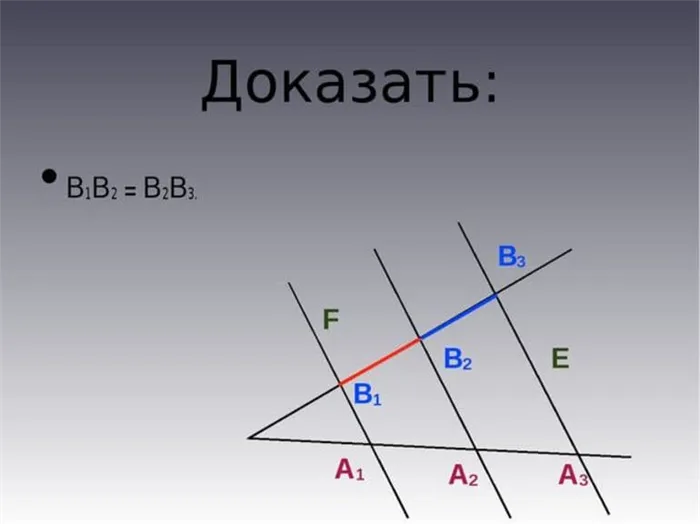
В качестве примера можно взять точки H1, H2 и H3, которые служат для отображения пересечения параллельных отрезков, используемых только на одной стороне угла. Однако пересечения этих линий на другой стороне угла — это K1, K2 и K3. Если провести короткие прямые T1 и T2 через K2 и параллельно H1 и H2, то получится параллелограмм: H1T1KH2 и H2K2T2H3. Из этого результата получаем, что H1H2 = T1K2 и H2H3 = K2T2. Этот результат был получен потому, что H1H2 = H2H3 и T1K1 = K2T2.

Интересные нюансы из истории

Обобщение теоремы позволило современным математикам понять пропорциональность данной части. Действующее правило гласит, что параллельные прямые, пересекающие стороны угла, пересекают соответствующие отрезки. Формула выглядит следующим образом: AA1 || VV1 || TT1 → AV OS = A1V1/ V1T1 .

Применение обобщенной теоремы имеет несколько интересных исторических фактов:

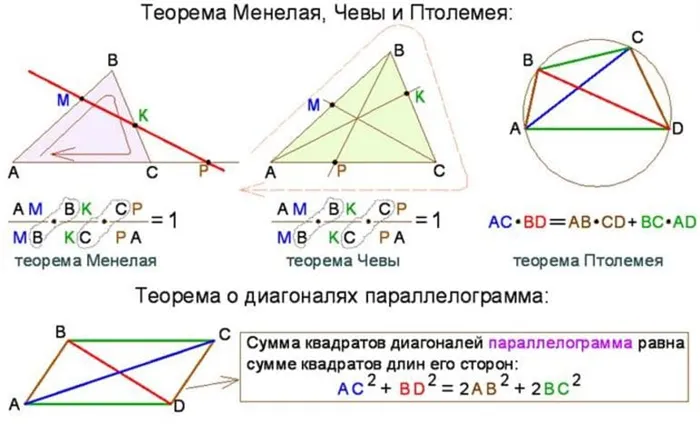
Теорема талантливого греческого ученого активно рассматривается на уроках геометрии в 8 классе.

Вариации и обобщения

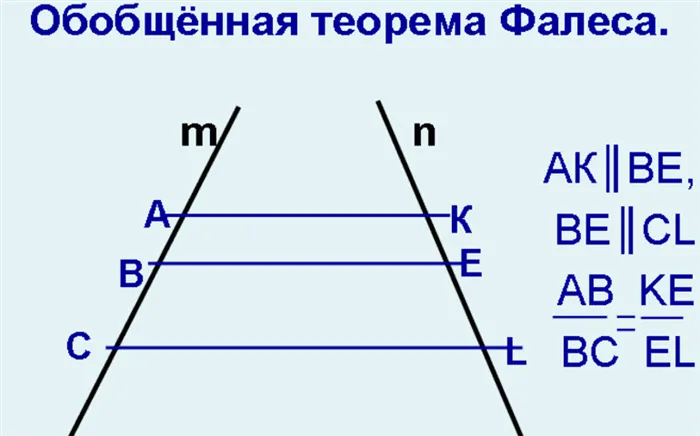
Теорема Фалеса с доказательством, используемая в геометрии, имеет множество нюансов, которые следует учитывать тем, кто решил изучать этот предмет. Если совершенно подобные отрезки начинаются в вершине треугольника, то обратная форма теоремы также применима. Для пересекающихся прямых применяется следующая формулировка: если две прямые пересекают ближайшие прямые, сохраняя равные расстояния между ними, начиная от вершины, то эти прямые считаются параллельными. Эти нюансы часто не учитываются студентами, что приводит к серьезным ошибкам.

Максимальное сходство сегментов в обеих вторичных линиях должно быть обязательным, если вторичные линии параллельны. В противном случае утверждение становится неактуальным. Студентам полезно знать следующий закон: L — это математическое соответствие между двумя точками прямых w и q. Тогда элементарное множество прямых D L (D) — это множество касательных к коническому пересечению. В теореме, установленной Фалесом, коническое пересечение — это удаленная точка, соответствующая максимуму в направлении параллельных прямых.

Знаете ли вы, что Фалес Милетский был одним из семи самых известных мудрецов Греции того времени? Он основал ионийскую школу. Идея, которую отстаивал Фалес в этой школе, заключалась в единстве всего сущего. Мудрец верил, что существует единое начало, из которого проистекает все сущее.

Большой заслугой Фалеса Милетского является создание научной геометрии. Этот великий ученый смог создать индуктивную геометрию из египетского искусства измерения, основой которой является общее основание.

Помимо больших познаний в геометрии, Фалес также хорошо разбирался в астрономии. Он был первым, кто предсказал полное солнечное затмение. И произошло это не в современном мире, а еще в 585 году до нашей эры.

Фалес Милетский был человеком, который понял, что север можно точно определить по созвездию Малой Урсы. Но и это не было его последним открытием, поскольку он смог точно определить продолжительность года, разделить его на триста шестьдесят пять дней и определить время равноденствий.

Фалес действительно был способным и мудрым человеком. Он был не только превосходным математиком, физиком и астрономом, но и настоящим метеорологом и мог с большой точностью предсказать урожай оливок.

Но самое примечательное, что Фалес никогда не ограничивал свои знания научно-теоретической сферой, а всегда пытался доказать свои теории на практике. И самое интересное, что великий мудрец не концентрировался только на одной области своих знаний, но его интерес шел в нескольких направлениях.

Уже тогда мудрецу стало знакомо имя Фалес. Его значение для Греции было столь же велико, как имя Ломоносова для России. Конечно, его мудрость можно интерпретировать по-разному. Но можно с уверенностью сказать, что он обладал и изобретательностью, и практическими способностями, и в какой-то степени определенной отстраненностью.

Фалес Милетский был превосходным математиком, философом, астрономом, любил путешествовать, был купцом и бизнесменом, занимался торговлей, был также хорошим инженером, дипломатом, провидцем и принимал активное участие в политической жизни.

Ему даже удалось определить высоту пирамиды с помощью своей волшебной палочки и своей тени. Все происходило следующим образом. В солнечный день Фалес положил свою палочку на границу, где заканчивалась тень от пирамиды. Затем он подождал, пока длина тени от его палки сравняется с его ростом, и измерил длину тени от пирамиды. Таким образом, Фалес мог легко определить высоту пирамиды и доказать, что длина одной тени связана с длиной другой тени, так же как высота пирамиды связана с высотой палки. Этим он удивил даже фараона Амасиса.

Благодаря Фалесу все известные в то время знания были переведены в сферу научного интереса. Он смог довести результаты до уровня, пригодного для научного использования, подчеркнув определенный набор понятий. И, возможно, с помощью Фалеса началось последующее развитие античной философии.

Теорема Фалеса играет важную роль в математике. Она была известна не только в Древнем Египте и Вавилоне, но и в других странах, и послужила основой для развития математики. И в повседневной жизни, при строительстве зданий, дорог и т.д., без теоремы Фалеса не обойтись.

Теорема Фалеса в культуре

Теорема Фалеса известна не только в математике, но и в культуре. Однажды аргентинская музыкальная группа Les Luthiers исполнила песню, посвященную знаменитой теореме. В видеоклипе участники группы Les Luthiers специально для этой песни выполняют доказательство прямой теоремы о пропорциональных частях.

Какие прямые называются параллельными?
Где практически применяется теорема Фалеса?
О чем гласит теорема Фалеса?

Презентация ««Теорема Фалеса»» (8 класс) по математике – проект, доклад

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

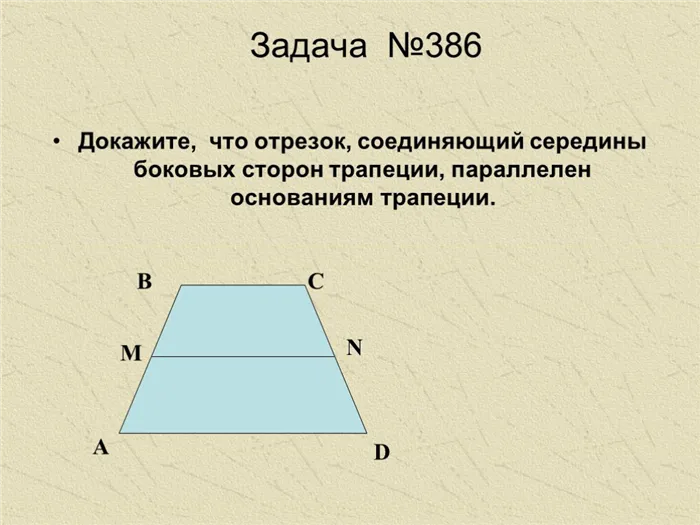
Слайд 19

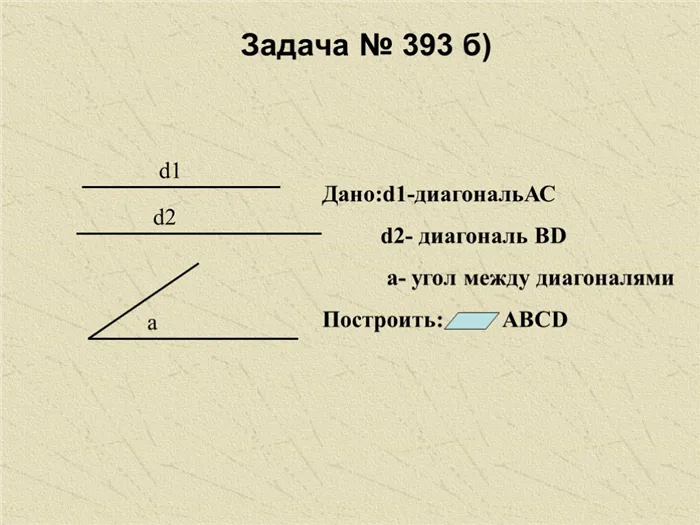
Слайд 20

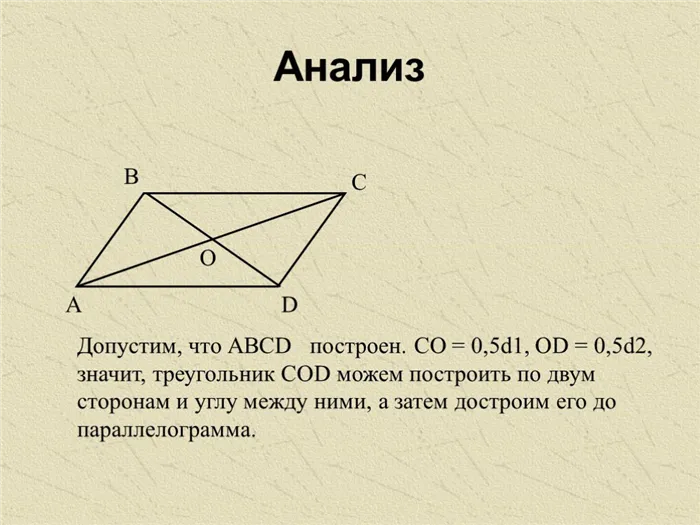
Слайд 21

Слайд 22

Слайд 23

Слайд 24

Презентацию на тему «Теорема Фалеса» (8 класс) можно скачать совершенно бесплатно с нашего сайта. Тема: Математика. Красочные слайды и иллюстрации помогут вам вдохновить своих одноклассников или слушателей. Используйте плеер для просмотра содержания или нажмите на соответствующий текст под плеером, если вы хотите скачать презентацию. Презентация содержит 24 слайда.

Слайды презентации

Урок 9 по геометрии, 8 класс Учитель: Федорова Т.Ф. Учебный год 2009-2010.

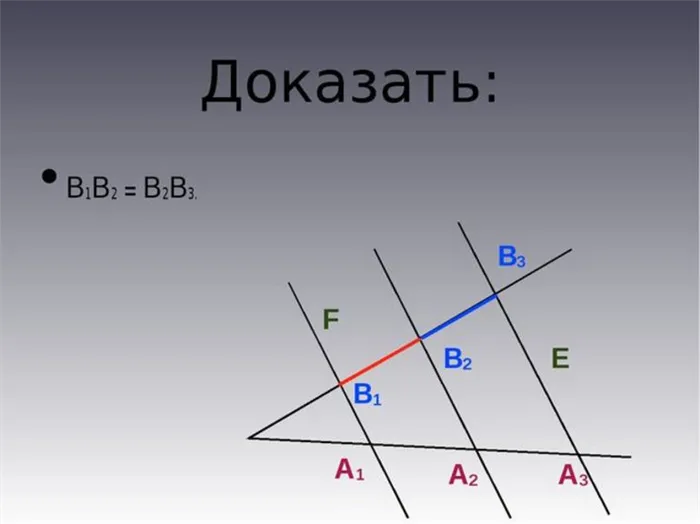
Изучите теорему Фалеса и подкрепите ее решением задач. Совершенствовать навыки решения задач, используя свойства равнобедренной трапеции и ее признаки, и применять знания о трапеции.

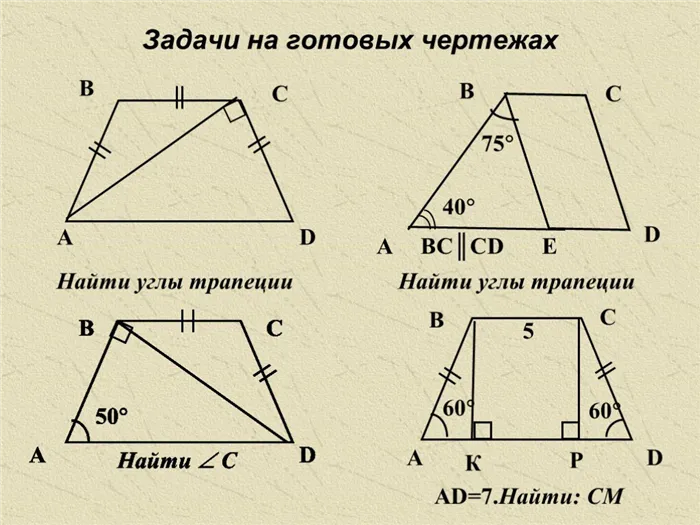
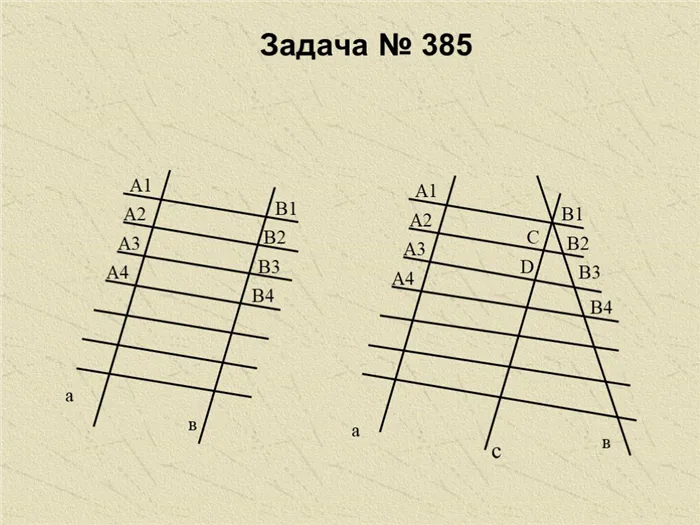
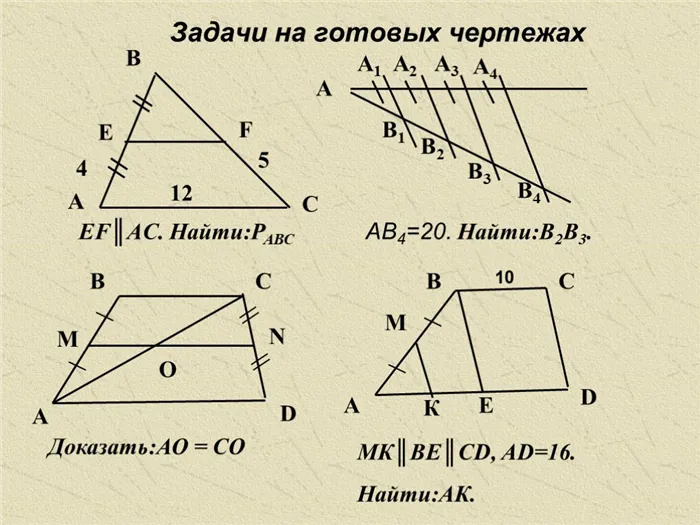
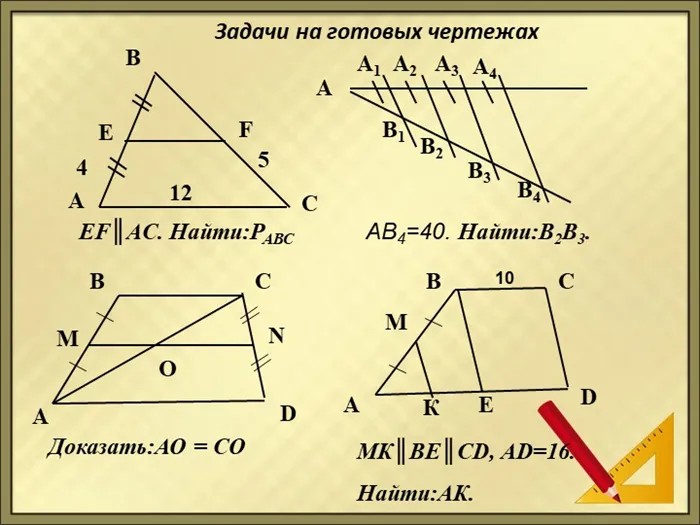
Проблемы с подготовленными чертежами

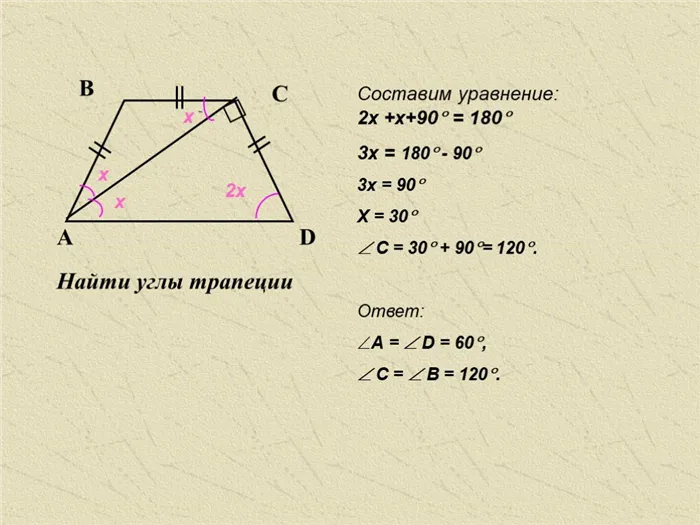
Найдите углы трапеции

75 40 A B C D E BC║CD 60 5 K P AD=7.Найти: CM

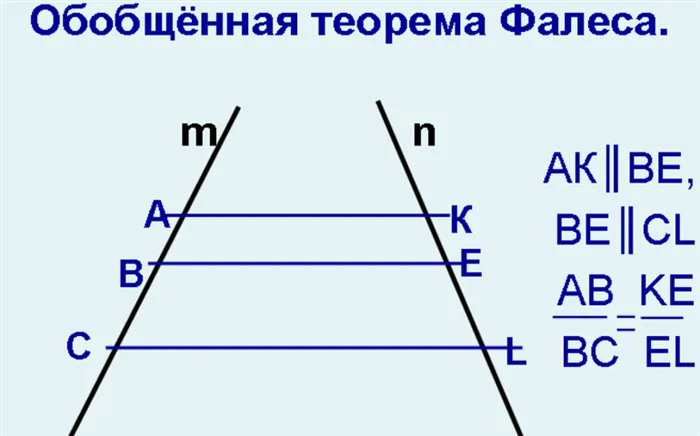
2x + x + 90 = 180 3x = 180 — 90 3x = 90 3x = 90 X = 30 C = 30 + 90 = 120.Ответ: Α = Δ = 60, Γ = Β = 120.

Ответы на проблемы

1. A = D = 60, B = C = 120. 2. A = 40, D = 65, C = 115, B = 140. 3. C = 100. 4. CM =2.

Великий ученый Фалес из Милета основал одну из самых прекрасных наук — геометрию. Хорошо известно, что Фалес Милетский носил титул одного из семи мудрецов Греции, что он действительно был первым философом, первым математиком, астрономом и вообще первым во всех науках в Греции. Короче говоря, он был для Греции тем же, чем Ломоносов был для России.

Он начал свою карьеру в качестве торговца и в молодости отправился в Египет. В Египте Фалес пробыл много лет и изучал науки в Фивах и Мемфисе. Считается, что он принес в Грецию геометрию и астрономию.

Фалес был математиком. Он измерил высоту пирамиды с помощью тени; обнаружил, что если круг с диаметром разделить посередине, то углы при основании равнобедренного треугольника равны. Часть теоремы заключается в том, что вписанный угол, который задается диаметром окружности, является правильным.

Некоторые изречения Фалеса сохранились до наших дней, например, следующее:

Список похожих презентаций

Урок по теме: «Теорема Пифагора»

Исторический обзор. Пифагор был греческим ученым, жившим в 6 веке до нашей эры. В целом можно утверждать, что о жизни и творчестве Пифагора, …

«Теорема Пифагора»

ПИТХАГОРАС. Помните, что сказал всем Гаусс: «Наука математика — царица всех наук», не зря он ее оставил — Творить в огне трудов и мучений. Так что работа науки и работа науки.

Начертательная геометрия

Начертательная геометрия изучает способ представления пространственных форм на плоскости. ГАСПАР МОНЖ. В 1795 году была опубликована работа под названием «Начертательная геометрия».

Что такое геометрия

Геометрия — одна из древнейших наук. Первые геометрические факты были найдены…. В вавилонских клинописных табличках и в египетских свитках (III .

«Ломаная» геометрия

Найдите соответствие. Ответы. Ломаная фигура Тема урока: какие из фигур являются ломаными? A B C D D. Ответ A C D. Возьмите кусок проволоки и согните его.

Пчелы и геометрия

Внеклассное мероприятие «Пчелы и геометрия». В природе все продумано и идеально. Индийская пчела Украинская пчела. Австралийская пчела. Пчела — .

Фракталы – геометрия природы

Цели:. узнать, что такое «фракталы»; изучить историю появления и развития фрактальной геометрии; познакомиться с биографией создателя фракталов.

Перпендикулярность в пространстве геометрия

Цель: Знакомство с вертикалью в пространстве. Анализировать различные источники информации по теме. Определите основные подходы, которые необходимо рассмотреть.

Построение сечений многогранников геометрия

Цель обучения: Развить навыки и умения по сборке деталей. Цель развития: формирование и развитие пространственного воображения учащихся. …

Векторы геометрия

Агентства. Действия с векторами. a b. Сумма векторов. Векторный коэффициент AC AN AM CB CM. Произведение векторов. Выразите вектор OM. M является пересечением .