Прямоугольник широты и долготы не следует путать с телесным углом прямоугольной пирамиды. Все четыре стороны прямоугольной пирамиды пересекают поверхность сферы по дугам большого круга. В прямоугольнике широты и долготы только долготы являются дугами большого круга; широты отсутствуют.
Телесный угол

Телесный угол — это участок пространства, который является объединением всех лучей, исходящих из определенной точки (вершины угла) и пересекающих поверхность (так называется поверхность, сжимающая телесный угол). Особыми случаями телесных углов являются тетраэдральные и полиэдральные углы. Граница телесного угла представляет собой конусообразную поверхность.
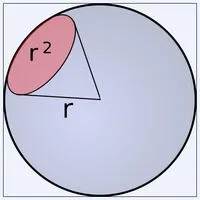
Телесный угол измеряется отношением площади части сферы с центром в вершине угла, пересекаемого телесным углом, к квадрату радиуса сферы:
Очевидно, что телесные углы измеряются абстрактными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, который соответствует телесному углу, вырезанному сферой с радиусом. Телесный угол сферы равен полному телесному углу ) для вершины, расположенной внутри сферы, особенно для центра сферы; он же — телесный угол, под которым любая замкнутая поверхность видна из точки, полностью окруженной, но не принадлежащей этой поверхности. Помимо стерадиана, телесные углы могут измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях от общего телесного угла.
Телесный угол имеет физическое измерение, равное нулю.
Обычно он обозначается буквой
Двойной телесный угол при заданном телесном угле определяется как угол, составленный из лучей, образующих неострый угол с любым радиусом угла.
Коэффициенты пересчета для единиц измерения телесных углов.
| Steradian | Градусы кв. | kv. Минута | Kv. второй | Общий угол | |
|---|---|---|---|---|---|
| 1 Стерадиан = | 1 | (180/π)² ≈ ≈ 3282,806 квадратных градусов | (180×60/π)² ≈ 1.1818103-10 7 квадратных минут | (180×60×60/π)² ≈ 4.254517-10 10 квадратных секунд | 1/4π ≈ 0,07957747 от общего угла |
| 1 квадратный градус = | (π/180)² ≈ 3,0461742-1 0-4 стерадиана | 1 | 60² = = 3600 квадратных минут | (60×60)² = 12,960,000 квадратных секунд | π/(2×180)²²² ≈ 2.424068-1 0-5 полный угол |
| 1 квадратная минута = | (π/(180×60))² ≈ ≈ 8.461595-1 0-8 стерадиан | 1/60² ≈ 2,7777778-1 0-4 квадратных градуса | 1 | 60² = = 3600 квадратных секунд | p/(2×180×60)² ≈ ≈ 6,73352335-1 0-9 полный угол |
| 1 квадратная секунда = | (π/(180×60×60)²² ≈ ≈ 2.35044305-1 0-11 стерадиан | 1/(60×60)² ≈ 7.71604938-1 0-8 Квадратный градус | 1/60² ≈ 2,7777778-1 0-4 квадратных минуты | 1 | p/(2×180×60×60)² ≈ ≈ 1.87042315-1 0-12 Общий угол |
| Общий угол = | 4π ≈ 12.5663706 Стерадиан | (2×180)²/π ≈ 41252,96125 квадратных градусов | (2×180×60)²/π ≈ 1,48511066-10 8 квадратных минут | (2×180×60×60)²/π ≈ ≈ 5,34638378-10 11 квадратных секунд | 1 |
- Полный телесный угол (полная сфера) равен
- Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.
- Треугольник с координатами вершин, , виден из начала координат под телесным углом
_1\mathbf_2\mathbf_3)>
где _2\mathbf_3)» width=»» height=»» />— смешанное произведение данных векторов, _j)» width=»» height=»» />- являются скалярными произведениями соответствующих векторов, жирными буквами обозначены векторы, обычными буквами — их длина. С помощью этой формулы можно вычислить телесные углы, ограниченные любым многоугольником с известными координатами вершин (просто разделите многоугольник на непересекающиеся треугольники).
- Телесный угол при вершине прямого кругового конуса с углом раствора α равен )» width=»» height=»» />. Если известны радиус основания конуса, то>)» width=»» height=»» />. Когда угол раствора конуса мал, » width=»» height=»» />( (
- Телесный угол двугранного угла в стерадианах равен удвоенному значению двугранного угла в радианах:
- Телесный угол трёхгранного угла выражается по теореме Люилье через его плоские углы
\left( \frac\right) \operatorname \left( \frac\right) \operatorname \left( \frac\right) \operatorname \left( \frac\right)>» width=»» height=»» />, где » width=»» height=»» />— полупериметр. Через двугранные углы
- Телесный угол при вершине куба (или любого другого прямоугольного параллелепипеда) равен » width=»» height=»» />полного телесного угла, или » width=»» height=»» />стерадиан.
- Телесный угол, под которым видна грань правильного N-гранника из его центра, равна » width=»» height=»» />полного телесного угла, или » width=»» height=»» />стерадиан.
См. также
| Твердые углы в Wikimedia Commons ? |
- Угол
- Двугранный угол
- Трехгранный угол
- Многогранный угол
- Стереометрия
- Геометрические фигуры
- Физические величины
Фонд Викимедиа. 2010 .
Телесный угол
Твердый угол
Телесный угол — это пространственный отрезок, который является объединением всех лучей, исходящих из определенной точки (вершины угла) и пересекающих поверхность (поверхность, которая сужает определенный телесный угол). Особыми случаями телесных углов являются тетраэдральные и полиэдральные углы. Граница телесного угла представляет собой конусообразную поверхность. Обычно телесный угол обозначается буквой Ω. Телесный угол измеряется отношением площади сферы, центр которой лежит в вершине угла, к квадрату радиуса сферы:
Серидиан
Телесные углы измеряются отвлечёнными (безразмерными) величинами. Единицей измерения телесного угла в системе СИ является стерадиан, равный телесному углу, вырезающему из сферы радиуса r поверхность с площадью r 2. Полная сфера образует телесный угол, равный 4 π стерадиан ( полный телесный угол ), для вершины, расположенной внутри сферы, в частности, для центра сферы; таким же является телесный угол, под которым видна любая замкнутая поверхность из точки, полностью охватываемой этой поверхностью, но не принадлежащей ей. Кроме стерадианов, телесный угол может измеряться в квадратных градусах, квадратных минутах и квадратных секундах, а также в долях полного телесного угла. Телесный угол имеет нулевую физическую размерность. Двойственный телесный угол к данному телесному углу Ω определяется как угол, состоящий из лучей, образующих с любым лучом угла Ω неострый угол. Коэффициенты пересчёта единиц телесного угла.
| Steradian | Градусы кв. | kv. Минута | Kv. второй | Общий угол | |
|---|---|---|---|---|---|
| 1 Стерадиан = | 1 | (180/π)² ≈ ≈ 3282,806 квадратных градусов | (180×60/π)² ≈ 1.1818103-10 7 квадратных минут | (180×60×60/π)² ≈ 4.254517-10 10 квадратных секунд | 1/4π ≈ 0,07957747 полного угла |
| 1 квадратный градус = | (π/180)² ≈ 3,0461742-1 0-4 стерадиана | 1 | 60² = = 3600 квадратных минут | (60×60)² = 12,960,000 квадратных секунд | π/(2×180)²²² ≈ 2.424068-1 0-5 полный угол |
| 1 квадратная минута = | (π/(180×60))² ≈ ≈ 8.461595-1 0-8 стерадиан | 1/60² ≈ 2,7777778-1 0-4 квадратных градуса | 1 | 60² = = 3600 квадратных секунд | p/(2×180×60)² ≈ ≈ 6,73352335-1 0-9 полный угол |
| 1 квадратная секунда = | (π/(180×60×60)²² ≈ ≈ 2.35044305-1 0-11 стерадиан | 1/(60×60)² ≈ 7.71604938-1 0-8 Квадратный градус | 1/60² ≈ 2,7777778-1 0-4 квадратных минуты | 1 | p/(2×180×60×60)² ≈ ≈ 1.87042315-1 0-12 Общий угол |
| Общий угол = | 4π ≈ 12.5663706 Стерадиан | (2×180)²/π ≈ 41252,96125 квадратных градусов | (2×180×60)²/π ≈ 1,48511066-10 8 квадратных минут | (2×180×60×60)²/π ≈ ≈ 5,34638378-10 11 квадратных секунд | 1 |
Вычисление телесных углов
Для любой граничной поверхности S телесный угол Ω, под которым она видна из начала координат, равен — сферическим координатам элемента поверхности — его радиус-вектору, — единичному вектору, перпендикулярному к
Свойства телесных углов
- Полный телесный угол (полная сфера) равен 4 π стерадиан.
- Сумма всех телесных углов, двойственных к внутренним телесным углам выпуклого многогранника, равна полному углу.
- Треугольник с координатами вершин, , виден из начала координат под телесным углом
где — смешанное произведение данных векторов, — скалярное произведение соответствующих векторов, векторы выделены жирным шрифтом и их длины в обычной системе счисления. Эта формула может быть использована для вычисления телесных углов любого многоугольника с известными координатами вершин (достаточно разбить многоугольник на непересекающиеся треугольники).
- Телесный угол при вершине прямого кругового конуса с углом раствора α равен. Если известны радиус основания и высота конуса, то. Когда угол раствора конуса мал, ( выражено в радианах), или ( выражено в градусах). Так, телесный угол, под которым с Земли видны Луна и Солнце (их угловой диаметр примерно равен 0,5°), составляет около 6·10 −5 стерадиан, или ≈0,0005 % площади небесной сферы (то есть полного телесного угла).
- Телесный угол двугранного угла в стерадианах равен удвоенному значению двугранного угла в радианах.
- Телесный угол трёхгранного угла выражается по теореме Люилье через его плоские углы при вершине, как:
- Телесный угол при вершине куба (или любого другого прямоугольного параллелепипеда) равен полного телесного угла, или стерадиан.
- Телесный угол, под которым видна грань правильного N -гранника из его центра, равна полного телесного угла, или стерадиан.
Практическое применение править
- Определение силы света и яркости, а также соответствующих радиометрических величин силы излучения и яркости
- Расчет сферического избытка Е в виде сферического треугольника
- Расчет потенциалов с использованием метода граничных элементов (БЭМ)
- Оценка размера лигандов в металлических комплексах, см. Угол конуса лиганда
- Расчет электрического поля и напряженности магнитного поля вокруг распределения заряда
- Вывод закона Гаусса
- Расчет мощности излучения и излучения при теплопередаче
- Расчет сечений резерфордского рассеяния
- Расчет сечений комбинационного рассеяния света
- Телесный угол приема конуса из оптического волокна
Конус, сферическая крышка, полусфера
Поперечное сечение конуса (1) и сферического колпака (2) внутри сферы. На этом рисунке θ = A/2 и r = 1.
Телесный угол конуса с вершиной при вершине телесного угла и углом при вершине 2 θ — это площадь сферической шапки в единичной сфере.
Для малых & thetas ; ≈ 1 — & thetas ; 2 /2, это сводится к площади круга P & thetas ; 2 .
Приведенный выше результат получается путем вычисления следующего двойного интеграла с использованием элемента единичной площади в сферических координатах:
∫ 0 2 π ∫ 0 2 π ∫ 0 θ sin θ ′ d θ ′ d ϕ = ∫ 0 2 π d ϕ ∫ 0 θ sin θ ′ d θ ′ = 2 π ∫ 0 θ sin θ ′ d θ ′ = 2 π — cos θ ′ 0 θ = 2 π ( 1 — cos θ ) ^.<2\pi>\int _^\sin \theta ‘\,d\theta ‘\,d\phi =\int _^<2\pi>d\phi \int _^\sin \theta ‘\,d\theta ‘\,=2\pi \int _^\sin \theta ‘\,d\theta ‘\ =2\pi \left-\cos \theta ‘\right_^\ =2\pi \left(1-\cos \theta \right)\>
Эта формула также может быть выведена без использования арифметических операций. Более 2200 лет назад Архимед доказал, что площадь сферической шапки всегда равна площади круга, радиус которого равен расстоянию между краем сферической шапки и точкой пересечения оси симметрии шапки. 1 Этот радиус указан, как на диаграмме:
Поэтому для единичной сферы телесный угол купола определяется следующим образом:
При θ = π / 2 сферическая шапка становится полусферой с телесным углом 2 π.
Телесный угол увеличенного конуса такой же:
Это также телесный угол той части небесной сферы, которую астрономический наблюдатель может видеть на широте θ при вращении Земли. На экваторе видна вся небесная сфера, на полюсах — только ее половина.
Телесный угол, образованный частью сферического конуса, пересекаемой плоскостью, образующей угол c с осью конуса и проходящей через вершину конуса, можно вычислить по формуле 2
Например, если γ = — θ, то формула сводится к формуле, приведенной выше для сферического колпака: первый член становится π, а второй — π cos θ .
Тетраэдр
Пусть OABC — вершины тетраэдра с началом O, соединенного с треугольной гранью ABC, где векторные позиции вершин — A, B и C. Определите угол при вершине θaкак угол BOC, и мы определяем θb, θ.cсоответственно. Пусть будет двугранным углом между плоскостями, которые содержат тетраэдрическое лицо ОБПА и ОВС и определяют, соответственно. Телесный угол Ω, образуемый треугольной поверхностью ABC, равен a →, b →, c → \ ,\,>\ ,\,>>ϕ a b>ϕ a c>ϕ b c>
Это следует из теории сферической избыточности и приводит к аналогичной теореме о том, что «сумма внутренних углов плоского треугольника равна π» для суммы четырех телесных углов тетраэдра следующим образом:
Телесные углы произвольных размеров править
Телесный угол, образованный общей ( d — 1 ) -мерной сферической поверхностью единичной сферы в d-мерном евклидовом пространстве, может быть определен в произвольном числе измерений d. Этот коэффициент телесного угла часто необходим в расчетах со сферической симметрией. Он описывается следующей формулой
где Γ — гамма-функция. Если d — целое число, то гамма-функция может быть вычислена явно. 9 Из этого следует, что
Это дает ожидаемые результаты 4 π стерадиан для трехмерной сферы, ограниченной областью 4π r 2 и 2 π радиан для двумерного круга, ограниченного окружностью длиной 2π r. Это также дает несколько менее очевидное значение 2 для одномерного случая, когда одномерная «сфера» с центром в начале координат является интервалом — r, r, и ограничена двумя крайними точками.
Аналог векторной формулы для произвольной размерности был получен Аомото 10 11 и независимо Рибандо. 12 Он выражает его в виде бесконечного многомерного ряда Тейлора:
Для заданных d единичных векторов, определяющих угол, пусть V обозначает матрицу, образованную их объединением, так что i- й столбец равен, и. Переменные образуют многовариантную. Для «конгруэнтной» целой мультиэкспоненты мы определяем. Обозначение для означает переменную, аналогично для показателей степени. Следовательно, термин означает сумму по всем членам, в которых l появляется либо как первый, либо как второй индекс. Там, где этот ряд сходится, он сходится к телесному углу, определяемому векторами. v i →>>>v i →>>>α i j = v i → ⋅ v j → = α j i, α i i = 1 =>>\cdot>>=\alpha _,\alpha _=1>a i j, 1 ≤ i
Ссылки править
- ^ «Архимед на сферах и цилиндрах». Математические страницы. 2015 г.
- ^ a b Мазонка, Олег (2012). «Телесный угол конических поверхностей, многогранных конусов и пересекающихся сферических крышек». arXiv : 1205.1396 math.MG .
- ^ Хопф, Хайнц (1940). «Избранные главы геометрии» (PDF). ETH Zurich : 1–2.
- ^ Ван Остером, А; Strackee, J (1983). «Твердый угол плоского треугольника». IEEE Trans. Биомед. Англ. БМЕ-30 (2): 125–126. DOI : 10.1109 / TBME.1983.325207 .
- ^ Eriksson, Folke (1990). «О мере телесных углов». Математика. Mag. 63 (3): 184–187. DOI : 10.2307 / 2691141. JSTOR 2691141 .
- ^ «Теорема L’Huilier — от Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Проверено 19 октября 2015 .
- ^ «Сферический избыток — от Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Проверено 19 октября 2015 .
- ^ «Площадь прямоугольника широты и долготы». Математический форум @ Drexel. 2003 г.
- ^ Джексон, FM (1993). «Многогранники в евклидовом n-пространстве». Вестник Института математики и его приложений. 29 (11/12): 172–174.
- ^ Aomoto, Кадзухико (1977). «Аналитическая структура функции Шлефли». Nagoya Math. Дж. 68 : 1–16. DOI : 10.1017 / s0027763000017839 .
- ^ Бек, М .; Робинс, С .; Сэм, SV (2010). «Теоремы положительности для телесных многочленов». Вклад в алгебру и геометрию. 51 (2): 493–507. arXiv : 0906.4031. Bibcode : 2009arXiv0906.4031B .
- ^ Ribando, Jason M. (2006). «Измерение телесных углов за пределами третьего измерения». Дискретная и вычислительная геометрия. 36 (3): 479–487. DOI : 10.1007 / s00454-006-1253-4 .
- Джеффи, AH (1954). «Телесный угол, образуемый круглой апертурой в точечных и рассеянных источниках: формулы и некоторые таблицы». Rev. Sci. Instrum. 25. С. 349–354. Bibcode : 1954RScI. 25..349J. DOI : 10.1063 / 1.1771061 .
- Маскет, А. Виктор (1957). «Контурные интегралы телесного угла, ряды и таблицы». Rev. Sci. Instrum. 28 (3). п. 191. Bibcode : 1957RScI. 28..191M. DOI : 10.1063 / 1.1746479 .
- Найто, Минору (1957). «Метод вычисления телесного угла, образуемого круглой апертурой». J. Phys. Soc. Jpn. 12 (10). С. 1122–1129. Bibcode : 1957JPSJ. 12.1122N. DOI : 10,1143 / JPSJ.12.1122 .
- Пакстон, Ф. (1959). «Расчет телесного угла круглого диска». Rev. Sci. Instrum. 30 (4). п. 254. Bibcode : 1959RScI. 30..254P. DOI : 10.1063 / 1.1716590 .
- Гарднер, Р.П .; Карнесейл, А. (1969). «Телесный угол, ограниченный в точке круглым диском». Nucl. Instrum. Методы. 73 (2). С. 228–230. Bibcode : 1969NucIM..73..228G. DOI : 10.1016 / 0029-554X (69) 90214-6 .
- Гарднер, Р.П .; Verghese, К. (1971). «О телесном угле, образованном круговым диском». Nucl. Instrum. Методы. 93 (1). С. 163–167. Bibcode : 1971NucIM..93..163G. DOI : 10.1016 / 0029-554X (71) 90155-8 .
- Асвестас, Джон С.; Инглунд, Дэвид С. (1994). «Вычисление телесного угла, представленного плоской фигурой». Опт. Англ. 33 (12). С. 4055–4059. Bibcode : 1994OptEn..33.4055A. DOI : 10.1117 / 12.183402 .
- Трика, Станислав (1997). «Угловое распределение телесного угла в точке, охватываемой круговым диском». Опт. Commun. 137 (4–6). С. 317–333. Bibcode : 1997OptCo.137..317T. DOI : 10.1016 / S0030-4018 (96) 00789-4 .
- Прата, MJ (2004). «Аналитический расчет телесного угла, полученного дисковым детектором с точечным косинусом». Nucl. Instrum. Методы Phys. Res.. 521. п. 576. arXiv : math-ph / 0305034. Bibcode : 2004NIMPA.521..576P. DOI : 10.1016 / j.nima.2003.10.098 .
- Тимус, DM; Прата, MJ; Калла, SL; Аббас, Мичиган; Oner, F .; Галиано, Э. (2007). «Некоторые дальнейшие аналитические результаты о телесном угле, образованном в точке круглым диском, с использованием эллиптических интегралов». Nucl. Instrum. Методы Phys. Res.. 580. С. 149–152. Bibcode : 2007NIMPA.580..149T. DOI : 10.1016 / j.nima.2007.05.055 .
Телесные углы произвольных размеров править
- ^ «Архимед на сферах и цилиндрах». Математические страницы. 2015 г.
- ^ a b Мазонка, Олег (2012). «Твердый угол конических поверхностей, многогранных конусов и пересекающихся сферических крышек». arXiv : 1205.1396 math.MG .
- ^ Хопф, Хайнц (1940). «Избранные главы геометрии» (PDF). ETH Zurich : 1–2.
- ^ «Теорема L’Huilier — от Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Проверено 19 октября 2015 .
- ^ «Сферический избыток — от Wolfram MathWorld». Mathworld.wolfram.com. 2015-10-19. Проверено 19 октября 2015 .
- ^ Eriksson, Folke (1990). «О мере телесных углов». Математика. Mag. 63 (3): 184–187. DOI : 10.2307 / 2691141. JSTOR2691141 .
- ^ Ван Остером, А; Strackee, J (1983). «Твердый угол плоского треугольника». IEEE Trans. Биомед. Англ. БМЕ-30 (2): 125–126. DOI : 10.1109 / TBME.1983.325207 .
- ^ «Площадь прямоугольника широты и долготы». Математический форум @ Drexel. 2003 г.
- ^ Джексон, FM (1993). «Многогранники в евклидовом n-пространстве». Вестник Института математики и его приложений. 29 (11/12): 172–174.
- ^ Aomoto, Кадзухико (1977). «Аналитическая структура функции Шлефли». Nagoya Math. Дж. 68 : 1–16. DOI : 10.1017 / s0027763000017839 .
- ^ Бек, М .; Робинс, С .; Сэм, SV (2010). «Теоремы положительности для полиномов телесного угла». Вклад в алгебру и геометрию. 51 (2): 493–507. arXiv : 0906.4031. Bibcode : 2009arXiv0906.4031B .
- ^ Рибандо, Джейсон М. (2006). «Измерение телесных углов за пределами третьего измерения». Дискретная и вычислительная геометрия. 36 (3): 479–487. DOI : 10.1007 / s00454-006-1253-4 .
- Джеффи, AH (1954). «Телесный угол, образуемый круглой апертурой в точечных и рассеянных источниках: формулы и некоторые таблицы». Rev. Sci. Instrum. 25. С. 349–354. Bibcode : 1954RScI. 25..349J. DOI : 10.1063 / 1.1771061 .
- Маскет, А. Виктор (1957). «Контурные интегралы телесного угла, ряды и таблицы». Rev. Sci. Instrum. 28 (3). п. 191. Bibcode : 1957RScI. 28..191M. DOI : 10.1063 / 1.1746479 .
- Найто, Минору (1957). «Метод вычисления телесного угла, образуемого круглой апертурой». J. Phys. Soc. Jpn. 12 (10). С. 1122–1129. Bibcode : 1957JPSJ. 12.1122N. DOI : 10,1143 / JPSJ.12.1122 .
- Пакстон, Ф. (1959). «Расчет телесного угла круглого диска». Rev. Sci. Instrum. 30 (4). п. 254. Bibcode : 1959RScI. 30..254P. DOI : 10.1063 / 1.1716590 .
- Гарднер, Р.П .; Карнесейл, А. (1969). «Телесный угол, ограниченный в точке круглым диском». Nucl. Instrum. Методы. 73 (2). С. 228–230. Bibcode : 1969NucIM..73..228G. DOI : 10.1016 / 0029-554X (69) 90214-6 .
- Гарднер, Р.П .; Verghese, К. (1971). «О телесном угле, образованном круговым диском». Nucl. Instrum. Методы. 93 (1). С. 163–167. Bibcode : 1971NucIM..93..163G. DOI : 10.1016 / 0029-554X (71) 90155-8 .
- Асвестас, Джон С.; Инглунд, Дэвид К. (1994). «Вычисление телесного угла, представленного плоской фигурой». Опт. Англ. 33 (12). С. 4055–4059. Bibcode : 1994OptEn..33.4055A. DOI : 10.1117 / 12.183402 .
- Трика, Станислав (1997). «Угловое распределение телесного угла в точке, охватываемой круговым диском». Опт. Commun. 137 (4–6). С. 317–333. Bibcode : 1997OptCo.137..317T. DOI : 10.1016 / S0030-4018 (96) 00789-4 .
- Прата, MJ (2004). «Аналитический расчет телесного угла, полученного дисковым детектором с точечным косинусом». Nucl. Instrum. Методы Phys. Res.. 521. п. 576. arXiv : math-ph / 0305034. Bibcode : 2004NIMPA.521..576P. DOI : 10.1016 / j.nima.2003.10.098 .
- Тимус, DM; Прата, MJ; Калла, SL; Аббас, Мичиган; Oner, F .; Галиано, Э. (2007). «Некоторые дальнейшие аналитические результаты о телесном угле, образованном в точке круглым диском с использованием эллиптических интегралов». Nucl. Instrum. Методы Phys. Res.. 580. С. 149–152. Bibcode : 2007NIMPA.580..149T. DOI : 10.1016 / j.nima.2007.05.055 .
Внешние ссылки править
- Теория многоугольника HCR (телесный угол, образуемый любым многоугольником) от Academia.edu
- Артур П. Нортон, Звездный Атлас, Галл и Инглис, Эдинбург, 1969.
- М.Г. Кендалл, Курс геометрии N измерений, № 8 Статистических монографий и курсов Гриффина, изд. М.Г. Кендалл, Charles Griffin & Co. Ltd, Лондон, 1961 г.
- Вайсштейн, Эрик В.«Твердый угол». MathWorld .
| Линейные/трансляционные переменные | Угловые/вращательные переменные | ||||||
| Линейные/поперечные переменные Угловые/вращательные переменные | 1 | L | L 2 | Линейные/поперечные переменные Угловые/вращательные переменные | 1 | 1 | 1 |
|---|---|---|---|---|---|---|---|
| Т | Время : t s | Спуск : A m s | Т | Время : t s | |||
| 1 | Расстояние: d, Положение: r, s, x, Перемещение m | Площадь : A м 2 | 1 | Угол : θ, угловое смещение : θ рад | Твердый угол : Ω рад 2, ср | ||
| Т −1 | Частота: f s-1, Гц | скорость : v, скорость : v m s-1 | кинематическая вязкость : n, удельный угловой момент : h m 2 s-1 | Т −1 | Частота: f s-1, Гц | угловая скорость : ω, угловая скорость : ω рад с-1 | |
| Т −2 | Ускорение : а м с-2 | Т −2 | Угловое ускорение : a рад с-2 | ||||
| Т −3 | Нарушение: J m s-3 | Т −3 | Угловое давление : Дж рад с-3 | ||||
| M | Масса : м кг | Стационарное положение: M ⟨x⟩ = ∑ mx | ML 2 | Момент инерции : I кг м 2 | |||
| M T-1 | Момент : p, Импульс : Дж кг м с-1, Н с | Действие: 𝒮, Сила: ℵ кг м 2 с-1, Дж с | ML 2 T l-1 | Угловой момент: L, угловой момент: Δ L кг м 2 с-1 | Действие: 𝒮, Сила: ℵ кг м 2 с-1, Дж с | ||
| M T-2 | Сила : F, Вес : FGМасса: м с-2, Н | Энергия: E, Работа: W, Лагранж: L кг м 2 с-2, J | ML 2 T-2 | Крутящий момент : t, Крутящий момент : М кг м 2 с-2, Н | Энергия: E, Работа: W, Лагранж: L кг м 2 с-2, J | ||
| М Т-3 | Травма : Y кг м с-3, N с-1 | Инерция: P кг м 2 с-3, W | ML 2 T-3 | Мощность: P кг м 2 с-3, Н м с-1 | Инерция: P кг м 2 с-3, W | ||








