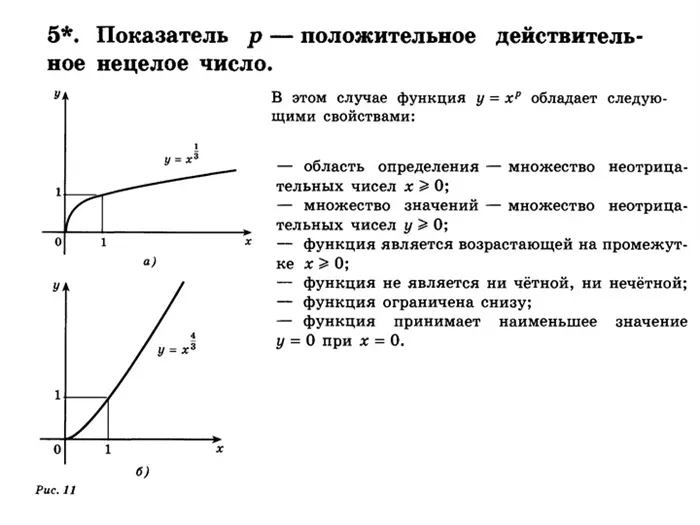
Область данной функции включает все действительные числа. Сначала постройте график функции y=x 4, затем переместите график вдоль оси крайнего положения на 1 единицу влево, а затем вдоль оси ортогонального положения на 1 единицу вниз. График показан на рисунке 11.
Свойства степенных функций, построение графиков
Теоретические функции мощности включают следующие формулы:
- линейная функция \(y = kx + b\) ;
- квадратичная парабола \(y = x^\) (в общем виде: \(y = ax^ + bx + c)\) ;
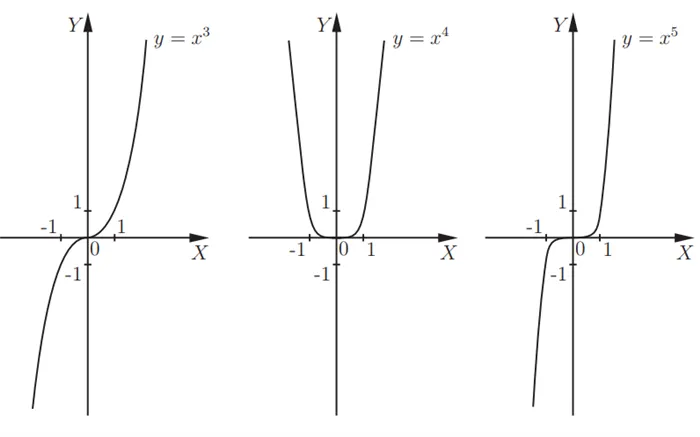
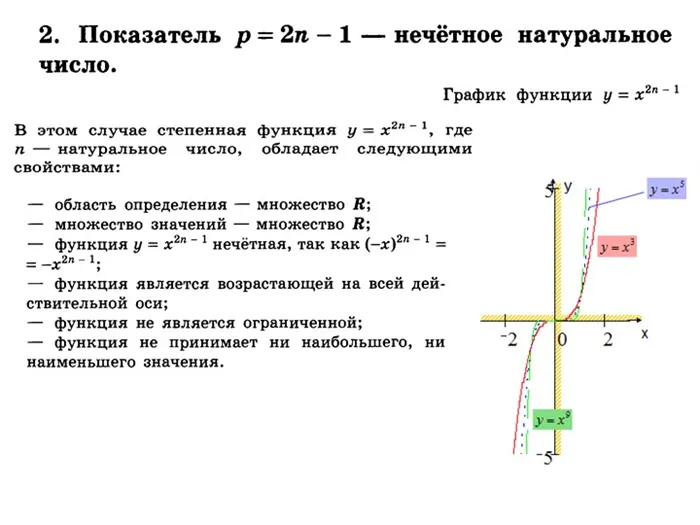
- кубическая парабола \(y = x^\) ;
- гипербола \(y = \frac\), которую можно представить в виде \( y = x^;\)
- функция \(y =\sqrt\), так как \(\sqrt = x^<\frac>.\)
В качестве примера можно рассмотреть описание функции: \(y=x^>\). В первую очередь следует проанализировать функции с показателем степени \(\frac>1\). Например, учитывая определенную функцию:
Внимание! Если профессор обнаружит плагиат в вашей работе, вам не избежать значительных проблем (вплоть до отчисления). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Из обозначений ясно, что областью определения этой функции при x≥0 является радиус 0;+∞).
Затем напишите таблицу значений:
Затем вы можете сравнить различные функции мощности следующим образом:
Число 2,5 лежит между 2 и 3, поэтому можно предположить, что график этой функции также лежит между соответствующими графиками. Различные характеристики x могут быть построены для сравнения значений функций, зависящих от x:
Рекомендуется отображать все графики на одном рисунке. В первом случае \(0\(0)) все графики должны быть построены одинаково.
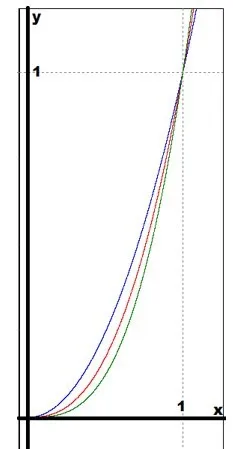
В данном случае синий цвет соответствует функции \(y=x^2\), красный: \(y=x^\); Зеленый: \(y=x^3\). Следующий шаг — построение графиков на всем диапазоне функции \(y=x^\) по порядку. Цвет графиков остается таким же, как и на предыдущем рисунке:
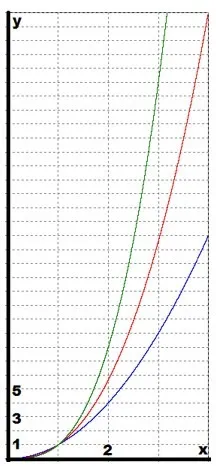
График функции \(y=x^>\), \((m>(n)\) — кривая, проходящая через точки (0,0) и (1,1) и напоминающая ветвь параболы. По мере увеличения экспоненты график функции становится круче к вершине.
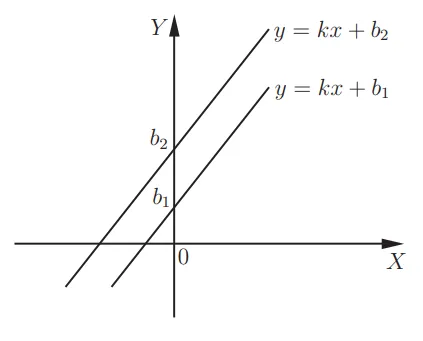
Линейная функция y = kx + b. Графиком данной функции является прямая линия. Для того, чтобы ее построить, требуется пара точек. При k>0, линейная функция будет возрастать. С увеличением k график становится более крутым. Значение k представляет собой угловой коэффициент прямой линии и равно тангенсу наклона этой прямой в положительном направлении оси x:
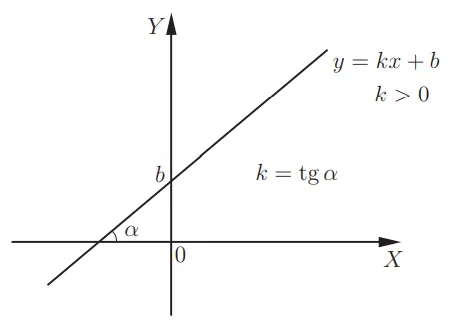
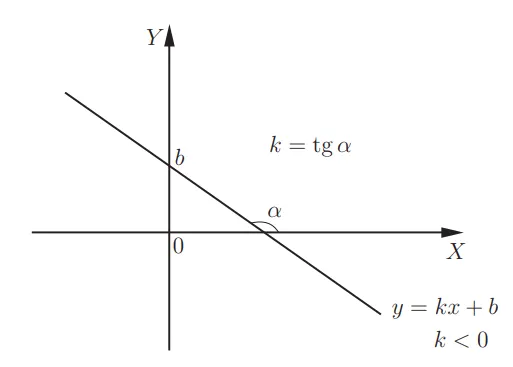
Когда k = 0, на графике изображена прямая y = b, которая параллельна оси x. Если угловые коэффициенты прямых равны, то прямые параллельны друг другу.
Квадратичная функция \(y = ax2 + bx + c\) является параболой. Он имеет некоторые особенности:
Виды и их свойства, область определения
Силовые функции обладают определенными особыми свойствами, которые могут отличаться в зависимости от типа. Давайте рассмотрим самые важные из них.
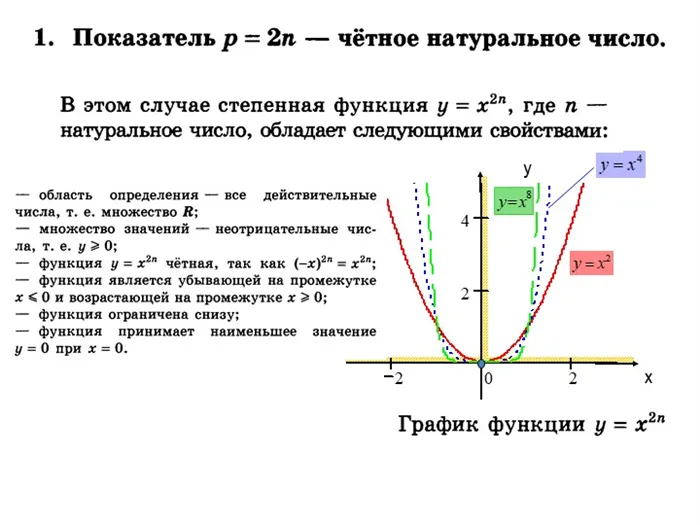
- D(y)=0;+∞);
- функцию нельзя отнести ни к четной, ни к нечетной;
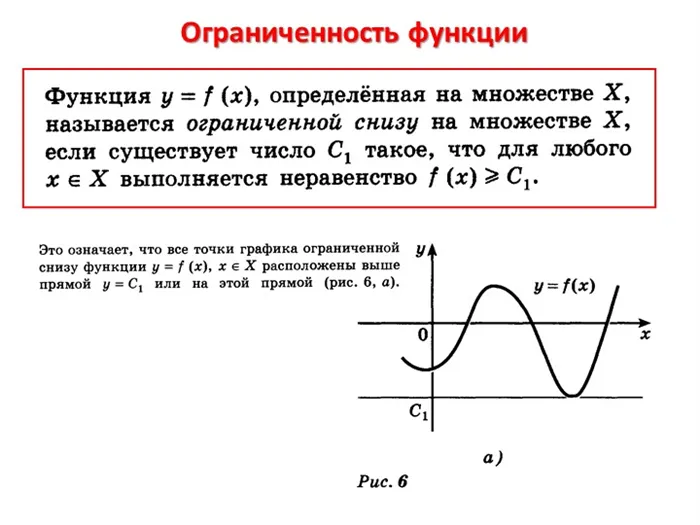
- возрастает на 0;+∞);
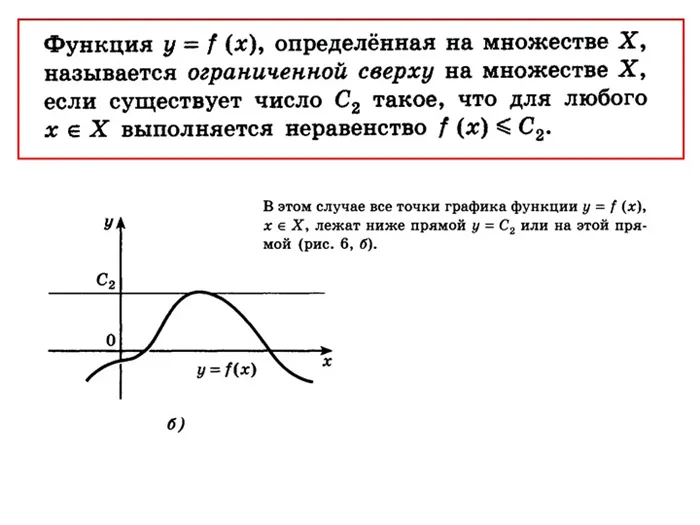
- не имеет ограничений в верхней части, но ограничена в нижней;
- отсутствует максимальное значение, минимальное значение равно нулю;
- непрерывность;
- E(f)=0; +∞);
- выпукла вниз.
В качестве примера можно рассмотреть случай, когда показатель степени является правильной дробью, у которой значение числителя меньше, чем знаменателя. График функции \( y=x^>\), \((m>n)\) выглядит как график функции \(y=\sqrtn\) :
- D(y)=0;+∞);
- нельзя отнести ни к четной, ни к нечетной;
- возрастает на 0;+∞);
- не имеет ограничений сверху, ограничена снизу;
- максимальное значение отсутствует, наименьшее значение равно нулю;
- непрерывность;
- E(f)=0; +∞);
- выпукла вверх.
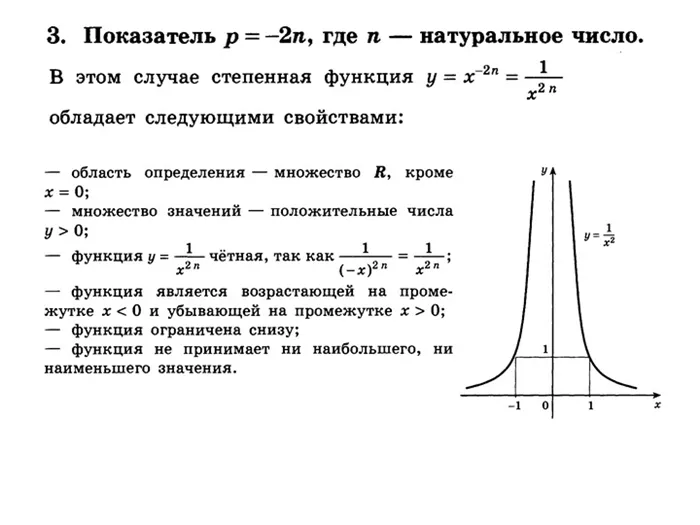
Далее следует ознакомиться с графиком функции \(y=x^>\). Вы заметите, что это выглядит как преувеличение. График имеет две асимптотические точки:
График имеет следующий вид:
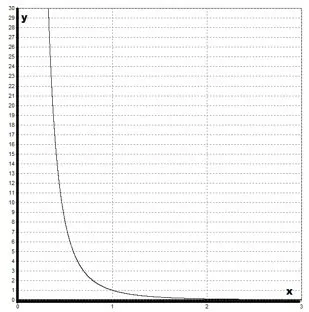
- D(y)=(0;+∞);
- не является ни четной, ни нечетной;
- убывает на (0;+∞);
- не ограничена в верхней части, обладает ограничением в нижней;
- максимальное значение отсутствует, минимальное – ноль;
- непрерывность;
- E(f)=(0; +∞);
- выпукла вниз.
В том случае, когда x>0 и r — рациональное число, производная степенной функции \(y=x^r\) определяется по формуле:
Степенная функция с рациональным и иррациональным показателем
Мощность действительного числа a с рациональной экспонентой n вычисляется по следующему уравнению:
Функция \( f(x)=x^(r\in Q)\) является степенной функцией с рациональной экспонентой.
Степенью числа a, которое является положительным, c иррациональным показателем \(\alpha\) называется выражение вида \(a^\) со значением, равным пределу последовательности \(a^>\), \(a^>, a^>\), …, где \(\альфа_, \альфа_, \альфа_\) — последовательные десятичные приближения иррационального числа \(\альфа\).
Функция \(f(x)=x^(r\in J)\) является степенной функцией с иррациональной экспонентой.
Презентация к уроку алгебры в 10 классе «Степенная функция, её свойства и график» (учебник Алимова и др.)

В настоящее время в общей сложности 54 257 учебных заведений предлагают накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.
Курсы повышения квалификации
Актуальные вопросы педагогики и методологии общего образования
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег участвовали в курсах «Инфорурок»)
В настоящее время в общей сложности 54 257 учебных заведений предлагают накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.
Курсы повышения квалификации
Профилактика синдрома «профессионального выгорания» у педагогов
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег участвовали в курсах «Инфорурок»)
В настоящее время в общей сложности 54 257 учебных заведений предлагают накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Инфорурок.


«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»
Описание презентации по отдельным слайдам:

1 слайд Класс 10 Силовая функция y=x p, ее свойства и график.



Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 990 311 Статья
Материал подходит для УМК
«Алгебра и зарождение математического анализа». Продвинутый и базовый уровни», А.Ш. Алимов, Ю.М. Колягин и др.
Тема
Другие материалы
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: § 5. Степень с рациональным и действительным показателями
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Учебник: «Алгебра», Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др.
- Учебник: «Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
- Тема: § 5. Правила раскрытия скобок
- Учебник: «Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
- Тема: § 7. Решение неравенств
- Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
- Тема: § 10. Числовые неравенства и их свойства
- Учебник: «Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
- Тема: § 28. Решение квадратных уравнений
- Учебник: «Алгебра», Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др.
Вам будут интересны эти курсы:
- Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
- Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
- Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
- Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
- Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
- Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
- Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
- Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
- Курс профессиональной переподготовки «Разработка эффективной стратегии развития современного вуза»
- Курс профессиональной переподготовки «Управление информационной средой на основе инноваций»
- Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
- Курс профессиональной переподготовки «Гражданско-правовые дисциплины: Теория и методика преподавания в образовательной организации»
Оставьте свой комментарий
Войдите в систему, чтобы задать свои вопросы.
- 01.10.2021 5849
- PPTX 2.1 мбайт
- 994 скачивания
- Рейтинг: 5 из 5
- Оцените материал:
Если вы считаете, что материал нарушает авторские права или должен быть удален с сайта по любой другой причине, вы можете подать жалобу на материал. Удаление материала








