Решение: Используйте переходные и комбинаторные свойства сложения и поменяйте местами суммы. Он подходит, если мы прибавим 38 к 12, 23 к 37, 46 к 54 и 15 к 40. Давайте сгруппируем суммы. Тогда сумма в первой скобке равна 50, сумма во второй скобке равна 60, сумма в третьей скобке равна 100 и сумма в последней скобке равна 55. Давайте посчитаем. Мы придумали 265.
Сложение натуральных чисел
Мы видим, что когда мы прибавляем 1 к натуральному числу, то получаем следующее натуральное число, то есть следующее число на единицу больше предыдущего. Теперь прибавьте 3 к 4: 4+3: Мы прибавляем 3 к 1, чтобы получить 4. Поскольку прибавление 1 к числу дает следующее число, мы имеем:
Но мы пишем для краткости: 4+3=7.
Числа, которые складываются, называютсясуммыа число, которое получается в результате сложения, называетсяСумма.
Сложение чисел на координатном луче
Мы хотим нарисовать линию координат. Отметьте на нем принцип координат, единичную часть и некоторые числа, которые следуют друг за другом:
Возьмем наш пример: 4+3. Чтобы добавить 3 к 4 на резонансном луче, мы добавим 3 единичных отрезка вправо от точки 4:
И мы приходим к точке 7, поэтому 4+3=7.
Теперь попробуем переместить 6 единичных отрезков на луче из точки 3 и 3 единичных отрезка из точки 6. Другими словами, мы добавим 6 к 3 и 3 к 6:
Мы видим, что и в первом, и во втором случае получается одна и та же точка: 9, поэтому сумма 3 и 6 и 6 и 3 одинакова и дает 9. Это можно записать равенством:
В этом случае мы поменяем местами суммы и получимпервое свойство сложения— транспонированное свойство :
Используя координатный радиус, рассмотрим следующие слагаемые: Из точки 3 сначала добавляем (6+7) единичных отрезков, затем из точки 3 сначала добавляем 6 единичных отрезков, затем из полученной точки добавляем еще 7 единичных отрезков:

Обратите внимание, что и в первом, и во втором случае мы приходим к одной и той же точке: 16. Это можно записать в терминах равенства:
Мы получиливторое свойство сложения— Второе комбинаторное свойство можно сформулировать следующим образом:
- Чтобы сложить сумму двух чисел с числом, мы можем сначала сложить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое
К положительному числу можно прибавить не только целое положительное число, но и ноль. Давайте воспользуемся радиусом, чтобы представить сложение нуля с 7:
Поскольку мы должны удалить единичные части из точки 0, мы вернемся в ту же точку, т.е. значение числа не изменилось от добавления нуля: 7+0=7. Используя свойство коммутативности, получаем: 7+0=0+7=7, т.е.третье свойство сложения— Свойство нуля:
- Если мы прибавим любое число к нулю, то получим добавленное число
Сравнение сумм натуральных чисел
Сравним (15+81) и (15+77), для этого рассмотрим слагаемые этих двух сумм: Мы видим, что первые слагаемые у них одинаковые, поэтому переходим к сравнению вторых слагаемых: 81>77, поэтому (15+81)>(15+77).
Теперь сравним (21+15) и (34+54), для этого снова посмотрим на суммы, в данном случае у нас нет одинаковых сумм, но мы видим, что сумма первого слагаемого меньше суммы второго слагаемого, поэтому мы можем написать: (21+15)
Бывают случаи, когда невозможно однозначно сказать, какая сумма больше. Например, если мы сравним суммы (26+33) и (18+43), то обнаружим, что первое слагаемое первой суммы больше первого слагаемого второй суммы, но второе слагаемое первой суммы меньше второго слагаемого второй суммы. В этом случае необходимо свести наши суммы к виду первого примера, т.е. 26=18+8, значит 26+33=(18+8)+33=18+8+33=18+41, теперь сравните (18+41) и (18+43), первые суммы равны, а 41
Из вышесказанного следует:Когда слагаемые увеличиваются, сумма увеличивается, а когда слагаемые уменьшаются, сумма уменьшается.
Что такое сложение?
Во-первых, что такое дополнение вообще? Сложение — одна из первых операций, изучаемых в школе, а иногда даже в детском саду. Обычно сложение объясняют на примере фруктов.
Если вы положите в корзину 3 груши и 2 яблока, то груши — это первое слагаемое, яблоки — второе, а общее количество фруктов в корзине — это сумма. Нельзя сказать, что это определение неверно, но количество студентов увеличивается с количеством используемых слов. Трудно представить себе, что к ним добавятся сотни тысяч фруктов.
Поэтому в математике используется другое определение, которое гласит, что сложение означает перемещение точки на числовой прямой вправо.
Большая часть знаний со временем усложняется. Например, если ученикам начальной школы говорят, что отрицательный результат сложения неверен, то к пятому классу они знают, что такой ответ возможен. То же самое относится и к определению дополнительных свойств. Обычных фруктов просто недостаточно для представления больших чисел. По этой причине теоретические определения преподаются в школе.
Свойства сложения
Они различают переходные и комбинаторные свойства. Свойство транспонирования гласит, что сумма не меняется от того, что меняются позиции слагаемых.
Комбинаторное свойство гласит, что в примерах, где есть два или более множителей, сложение может быть выполнено в любом порядке. В этом случае важно правильно сгруппировать суммы, чтобы ускорить вычисления и не усложнять их. Самый простой способ — посмотреть на количество единиц в числе. Первый способ заключается в сложении чисел, сумма которых равна 10, например, числа 29 и 31 составляют 60.
Затем вы складываете целые десятки, а затем остаток. Это самый простой и быстрый способ решения задач на сложение.
Разница между использованием комбинаторного свойства и переходного свойства непонятна даже учителю. Они очень похожи, и некоторые математики даже считают, что комбинаторное свойство является продолжением свойства преобразования. По этой же причине учителей редко просят отличать применение одного свойства от другого. Они просто должны уметь использовать и то, и другое.
Пример
Примеры комбинаторного свойства сложения найти несложно. Почти в каждом примере используется это свойство.
15*3+5-13-13-17-2-16-2 — начните с умножения.
45+5-13-13-17-2-16-2 — теперь сгруппируйте условия так, чтобы вы могли вычислить результат как можно быстрее. Помните, что разность можно представить как сумму отрицательных чисел. В нашем случае минус просто заключен в скобки.
45+5-13-17-2-16-2=(45+5)-(13+17)-(2+2+16) — теперь вычисляем в скобках и находим окончательный результат
Это ответ на довольно длинный пример. Не бойтесь простых ответов типа 0 или 1. Иногда составители примеров делают это, чтобы запутать студентов.
Сочетательный закон сложения.
Чтобы добавить третье число к сумме двух чисел, сумму второго и третьего чисел можно прибавить к первому числу.
( a+ b)+ c= a+( b+ c)
Закон сочетания применим к любому количеству слагаемых. Этот закон мы применяем при сложении чисел в любом порядке. Например, сложите три числа — 12, 6, 8 и 4. Удобнее сначала сложить 12 и 8, а затем прибавить сумму 6 и 4. (12+8)+(6+4)=30
Свойство сложения с нулем.
Если к нулю прибавить число, то в сумме получится то же самое число.
В алфавитном выражении добавление к нулю выглядит следующим образом:
a+0= a 0+ a= a
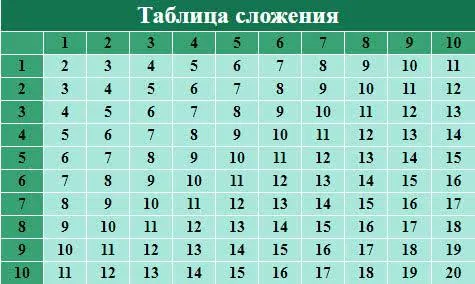
Вопросы по теме сложения натуральных чисел: Таблица сложения, сделайте и посмотрите, как работает свойство закона сложения? Таблица сложения от 1 до 10 может выглядеть следующим образом:
Вторая версия таблицы сложения.
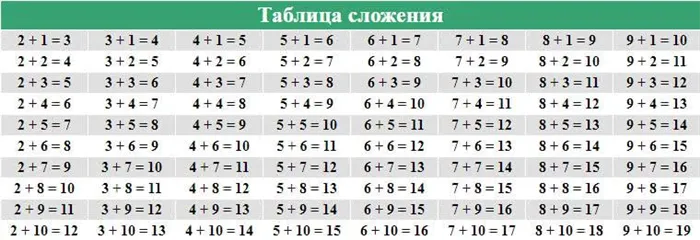
Рассматривая таблицы сложения, мы можем увидеть, как работает закон сложения.
Чему равна сумма выражения a+b=c? Ответ: Сумма — это результат сложения слагаемых a+b и c.
Что является суммой в выражении a+b=c? Ответ. Суммы — это числа, которые мы складываем вместе.
Что произойдет с числом, если добавить 0? Ответ: ничего, число не меняется. Если мы прибавляем к нулю, число остается неизменным, потому что ноль — это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы действовал комбинаторный закон сложения? Ответ: Три или более суммы.
Запишите комбинаторный закон сложения в буквенном выражении? Ответ: a+b=b+a
Примеры проблем. Пример №1: Напишите ответ следующих выражений: a) 15+7 b) 7+15 Ответ: a) 22 b) 22
Пример №2: Напишите закон комбинаторики для сумм: 1+3+5+2+9 1+3+5+2+9 1+3+5+2+9 1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20 Ответ: 20.
Пример 3: Решите выражение: а) 5921+0 б) 0+5921 Решение: а) 5921+0 =5921 б) 0+5921=5921
You may also like:

Десятичные дроби. Разряды и классы десятичных дробей.

Нужен репетитор по математике (алгебре) или геометрии?

Сравнение неправильных дробей правила и примеры.
Деление дробей. Правила. Примеры.
Добавить комментарийОтменить ответ
Прибавить одно число к другому довольно просто. Возьмем пример 6+3=9. Это выражение означает, что к шести единицам прибавили три единицы, и в результате получилось девять единиц. Или возьмем в качестве примера ряд чисел: сначала ряд был сдвинут на 6, затем на 3 и, наконец, на 9. Числа 6 и 3, которые мы сложили, называются слагаемыми. Сумма этих чисел называется суммой 9. В алфавитном порядке этот пример будет выглядеть так: a+b=c, где a — сумма, b — сумма и c — сумма. Если к трем единицам прибавить 6, то в сумме получится тот же результат — 9. Из этого примера можно сделать вывод, что даже если изменить слагаемые, ответ останется тем же: 6+3=3+6=9.
Свойства сложения. Законы сложения

Это свойство называется законом сложения.
Сумма не меняется, если поменять местами слагаемые.
Переместительный (коммуникативный) закон сложения: a + b = b + a.
55 + 21 = 21 + 55 = 76 108 + 2 = 2 + 108 = 110
Если сложить три суммы, скажем 1, 2 и 6, и выполнить сложение в таком порядке, сначала добавив к сумме 1 + 2, а затем 6, мы получим сумму: (1 + 2)+6 = 9 Мы добавляем 2 + 6, а затем добавляем к сумме 1. Ответ тот же, что и выше: 1+(2+6)=9. В обеих формулах сложения одного и того же примера ответ один и тот же. Schlussfolgerung: (1+2)+6=1+(2+6)
Это свойство сложения называется комбинаторным законом сложения.
Сумма не изменяется, когда группа соседних слагаемых заменяется своей суммой.
Сочетательный (ассоциативный) закон сложения: a + b + c = a + (b + c).
197 + 23 + 77 = 197 + (23 + 77) = 197 + 100 = 297.
Примечание от Учителя 7: Оба закона применимы к любому количеству слагаемых. Переходный и комбинаторный законы сложения применимы ко всем неотрицательным числам.
Постпозитивный и комбинаторный законы используются дополнительно для удобства и упрощения расчетов.
Сложение 23 + 9 + 7 Используя свойство коммутативности, поменяем местами суммы 9 и 7, получим 23 + 7 + 9. Теперь сложим 23 и 7 вместе, так как они составляют круглое число: (23 + 7) + 9, Сначала сложим 23 и 7, их сумма равна 30. Затем сложим девять: 30 + 9 = 39. Итак: 23 + 9 + 7 = (23 + 7) + 9 = 36








