Путем параллельного переноса соедините конец вектора a с началом вектора b. Затем соедините начальную точку вектора a с конечной точкой вектора b. Результат \(\vec c\). Длина отрезка, представляющего это направление, равна сумме \(\vec a\) и \(\vec b\) .
Сложение векторов: длина суммы векторов и теорема косинусов
Сложение векторов по правилу треугольника (векторная сумма и — это вектор, начало которого совпадает с началом вектора и конец которого совпадает с концом вектора, при условии, что начало вектора соединено с концом вектора) позволяет упростить выражение перед вычислением произведений векторов.
Сложение векторов, заданных координатами (сложение тех же координат, которые складываются), позволяет найти способ, которым вектор, являющийся суммой сложенных векторов, связан с началом координат. Эти две операции были подробно рассмотрены в уроке «Векторы и операции с векторами».

Теперь мы узнаем, как найти длину вектора, который получается в результате сложения векторов. Для этого мы воспользуемся теоремой косинусов. Такая проблема возникает, например, когда дорога из точки A в точку C не является прямой линией, а отклоняется от прямой и проходит через другую точку B, и нам нужно найти длину предполагаемой прямой линии. Кстати, геодезия — одна из областей, в которой тригонометрические функции применяются в полном объеме.
При сложении векторов теорема косинусов используется для нахождения длины суммы векторов. Пусть и векторы, — углы между ними, и — сумма векторов в результате сложения векторов по правилу треугольника. Тогда имеет место следующее соотношение:
Где — угол, прилежащий к углу. Смежные углы имеют общую сторону, а другие стороны лежат на одной прямой (см. рисунок выше).
Поэтому, чтобы сложить векторы и найти длину суммы векторов, нужно взять квадратный корень из каждой части равенства, а затем получить формулу длины:
При векторном вычитании () вектор прибавляется к вектору, противоположному вектору, то есть имеющему ту же длину, но противоположное направление. Углы между и и являются смежными, они имеют, как уже говорилось, общую сторону, а другие стороны лежат на одной прямой. Чтобы найти длину разности векторов при векторном вычитании, нужно знать следующее свойство косинусов смежных углов:
Значения косинусов смежных углов равны по абсолютной величине (величина по модулю), но имеют противоположные знаки.
Давайте продолжим с примерами.
Сложение векторов — решение примеров
Пример 1. Векторы и образуют угол. Сложите векторы и найдите их сумму. Вычтите векторы и найдите их разность.
Решение. Из элементарной тригонометрии мы знаем, что .
Шаг 1: Выполните сложение векторов. Найдите длину суммы векторов, указав в формуле длины косинус угла, смежного с углом между векторами:
Шаг 2. Выполните вычитание вектора. Найдите длину разности векторов, подставив в формулу косинус «исходного» угла:
Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение
Пример 2. Векторы и образуют угол. Их длина составляет: и. Сложите векторы и найдите их сумму. Вычтите векторы и найдите их разность.
Пример 3. Дайте длины векторов, длину их суммы и найдите длину их разности.
Шаг 1: Используя теорему косинусов, составьте уравнение для нахождения косинуса угла, касательного к углу между векторами и найдите :
Помните, что косинус прилежащего угла имеет знак минус. Это означает, что косинус «исходного» угла имеет знак плюс.
Шаг 2. Выполните вычитание вектора. Найдите длину разности векторов, подставив в формулу косинус «исходного» угла:
Пример 4. Найдите длину векторов, длину их разности и длину их суммы.
Шаг 1: Используя теорему косинусов, составьте уравнение для нахождения косинуса «исходного» угла (задача является обратной к примеру 1) и найдите его:
Шаг 2. Измените знак косинуса и получите косинус смежного угла между и :
Шаг 3: Выполните сложение векторов. Найдите длину суммы векторов, подставив в формулу косинус прилежащего угла:
Пример 5. Векторы и и перпендикулярны друг другу и их длины равны. Определите длину их суммы и длину их разности.
Как легко догадаться из определения, приведенного в начале урока, два смежных угла вместе дают 180 градусов. Поэтому угол, примыкающий к прямому углу (90 градусов), также является прямым углом (также 90 градусов). Косинус такого угла равен нулю, как и косинус соседнего угла. Поэтому если подставить это значение в выражения под корнем в формуле для длин суммы и разности векторов, то в качестве последних выражений — произведений под знаком корня — получатся нули. То есть длины суммы и разности данных векторов равны, вычислите их:
Пример 6. Какой формуле должны удовлетворять векторы и, чтобы выполнялись следующие соотношения.
1) длина суммы векторов равна длине разности векторов, т.е. ,
2) длина суммы векторов больше длины разности векторов. ,
3) длина суммы векторов меньше длины разности векторов, т.е. ?
Найдем условие для первого соотношения. Для этого решаем следующее уравнение:
То есть, чтобы длина суммы векторов была равна длине их разности, косинус угла между ними и косинус угла, касательного к ним, должны быть равны. Это условие выполняется, если углы образуют прямой угол.
Найдите условие для второй зависимости. Решите уравнение:
Найденное условие выполняется, если косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, углы должны образовывать острый угол (пример 1).
Мы находим условие для третьего отношения. Решите уравнение:
Найденное нами условие выполняется, если косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовывали тупой угол.
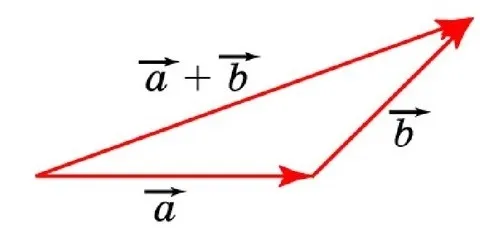
Как происходит сложение по правилу треугольника
Чтобы найти сумму векторов x и y, нужно провести первый из любой точки, а второй — через ее край. Следующий шаг — построение направленного отрезка, соединяющего начало \vec x с концом \vec y. Результирующая сторона треугольника является результатом сложения двух векторов. Теорема считается доказанной.
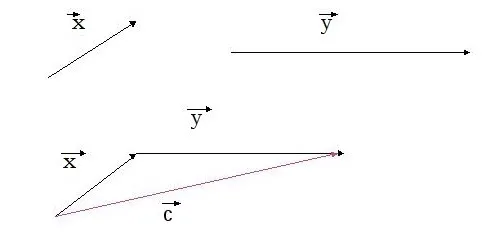
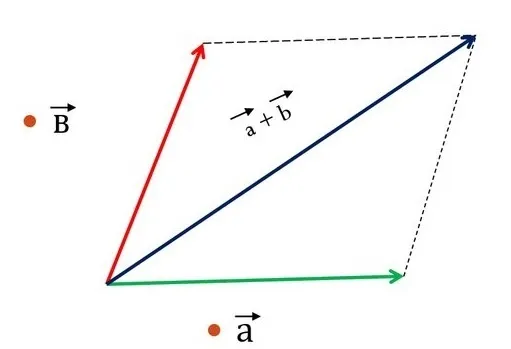
Сложение по правилу параллелограмма
Можно найти сумму векторов без построения треугольника. Для этого второй вектор должен быть проведен из начала координат первого вектора. Расширим полученный чертеж до параллелограмма. У нас уже есть две стороны. Метод параллельного переноса поможет при построении остальных. Диагональ конечной формы, начиная с начальной точки векторов, рассматривается как их сумма. Теорема доказана.
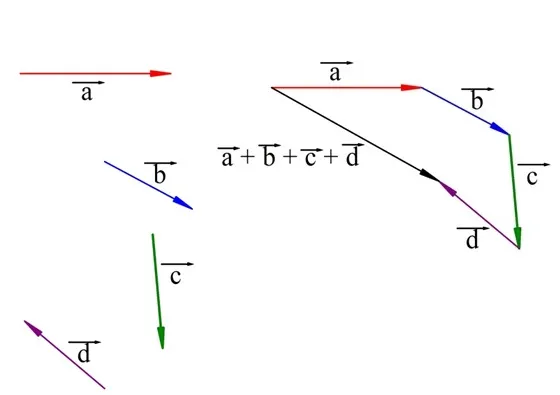
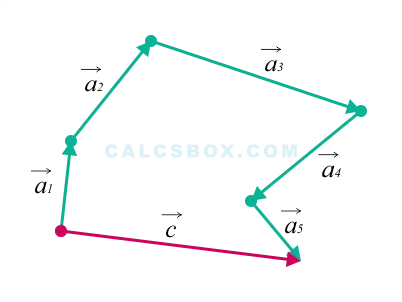
Как и когда применяется правило многоугольника
Этот метод необходим для сложения более двух векторов.
Принцип работы в этом случае аналогичен последовательности шагов для треугольника. Постройте первый вектор из любой точки. С его конца — второй, со второго — третий и так далее. Затем соедините конец последнего вектора с началом первого вектора — это будет результат сложения всех векторов. Доказательство теоремы выполнено.
Сложение векторов, Сумма векторов

Сумма векторов a и b является третьим вектором c, который получается следующим построением: Из любого начала координат O постройте вектор OL, равный a; из точки L, как из начала координат, постройте вектор LM, равный b. Вектор c = OM является суммой векторов a и b («правило треугольника»).
Следующие неравенства применимы к сложению векторов.
Эти неравенства показывают, что сторона OM треугольника OML меньше суммы и больше разности двух других сторон.
В формуле (1) символ равенства применяется только к векторам одного направления, в формуле (2) — только к векторам противоположного направления.

Если суммы a и b не являются смежными, то сумму a + b можно определить с помощью следующей конструкции.
Из любого начала координат O постройте векторы OA = a и OB = b; на отрезках OA, OB постройте параллелограмм OASB. Вектор диагонали OS = c является суммой векторов a и b (так как AC = OB = b и OS = OA + AC).
Эта конструкция не применяется к липким векторам.
Определение сложения векторов основано на физических законах сложения векторных величин (например, сил, действующих на материальную точку).








