Решение логарифмических неравенств. Как решать неравенства с логарифмами.

Если \(a\gt 1\), то логарифмическое неравенство \(\log_a f(x)\gt\log_a g(x)\) равносильно системе: \bginning \log_a f(x)\lt\log_a g(x)\left стрелка \beginning f(x)\gt g(x)\\\\\ f(x)\gt 0\\\\ g(x)\gt 0 \end \end \end Знак неравенства между \(f(x)\) и \(g(x)\) сохраняется.

Логарифмические неравенства

Кратко разберем общий алгоритм решения неравенств с логарифмами. Если хочешь разобраться подробно, изучив все детали, листай ниже. В общем виде логарифмическое неравенство можно записать в виде: $\log_f(x)>\log_g(x);$ где \(a>0, \quad a\neq1\) — основание логарифма; \(f(x)>0 \, ,g(x)>0\) — это определенные выражения, которые зависят от \(x\).

Важно, чтобы логарифмы слева и справа от знака неравенства были с одинаковым основанием! Только в этом случаем можно избавиться от логарифмов и сравнить подлогарифмические функции. Так и поступим — просто вычеркнем логарифмы и получим неравенство при \(a>1\): $f(x)>g(x);$

Но есть один момент, за которым важно внимательно следить. Дело в том, что мы рассмотрели случай только при основании логарифма \(a>1\), но что произойдет, если \(0 \lt a \lt 1? \) Оказывается, что и в этом случае мы избавляемся от логарифмов, но избавляемся от знака неравенства в обратном направлении!

При \(0 \lt a \lt 1\) неравенство будет выглядеть так: $f(x) \lt g(x);$

Как решать логарифмические неравенства?

Решение логарифмических неравенств аналогично решению обычных логарифмических уравнений. Однако есть несколько моментов, о которых следует помнить.

Если у вас возникли проблемы с вычислением логарифмов, я рекомендую сначала прочитать что-нибудь о логарифмах и их свойствах.

При этом нужно помнить про ограничения, которые накладываются на логарифм \(\log_b\): $ \begin b>0, \\ a>0, \a

Начнем изучение неравенств с небольшого примера: $\log_x>\log_4;$ Сравниваются два логарифма с ОДИНАКОВЫМ основанием, значит вполне логично предположить, что \(\log_x\) будет больше \(\log_4\), при условии, что \(x>eq 1. \end$

Действительно, согласно определению логарифма, чем больше \(х\), тем в бОльшую степень нужно возвести \(2-ку\) в основании логарифма, а значит, и тем больше будет сам логарифм. Подставим в неравенство \(х=16\) — число большее \(4\): $\log_16>\log_4;$ Посчитаем получившиеся логарифмы: $4>4\). Это решение простого неравенства.

И подставляя любые числа большие \(4\), вы всегда будете получать верное неравенство. Некоторые логарифмы мы не можем посчитать, как например \(\log_15\), но логика сохраняется, если подставлять \(x>4\), неравенство будет верным. Кстати, калькулятор вам любезно подскажет, что \(\log_15=3,907>\log_4\), что нас устраивает. Ответ: \(x>4\).

Теперь рассмотрим другой пример: $\log_>(x)>\log_>(4);$ Обратите внимание, я поменял основания на \(\frac\). Интересно, изменится ли логика рассуждений? Подставим \(х=16>4\): $\log_>(16)>\log_>(4);$ $\log_>(2^4)>\log_>(2^2);$ $\log_>((\frac)^)>\log_>((\frac)^);$ Посчитаем логарифмы слева и справа: $-4>2;$ Мы имеем верное неравенство.

-2;$ Упс, неверное неравенство! \(-4\), конечно, не больше \(-2\). Мы заменили левый логарифм на большее число, чем правый логарифм, но получили, что логарифм меньше. Другими словами: Если основание логарифма меньше единицы, то чем больше аргумент, который мы подставляем, тем меньше логарифм.

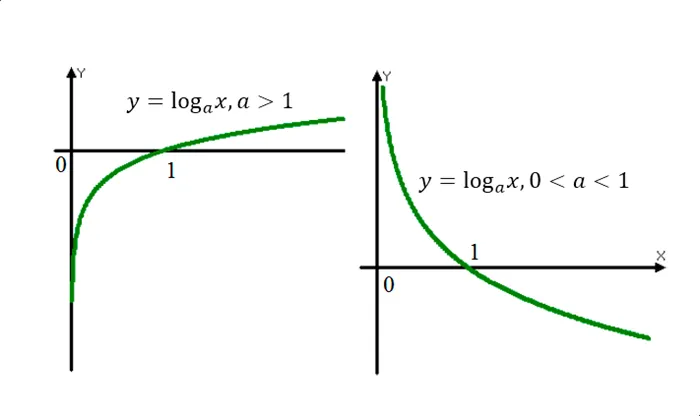
Для примера на рисунке показан график логарифмов \(\log_(x)\) с основанием 2 (красным цветом) — возрастающая функция. И \(log_>Оказывается, логарифм является возрастающей функцией, если основание логарифма больше единицы: чем больше аргумент, тем больше сам логарифм. Если основание логарифма меньше единицы, то логарифм является возрастающей функцией: чем больше значение аргумента, тем меньше значение самого логарифма.

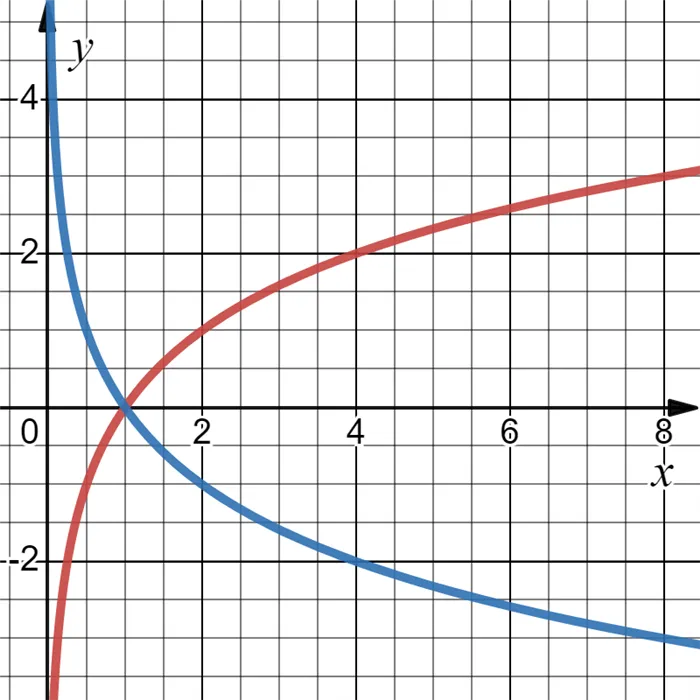
(x)\) на основе 0,5 показана синим цветом (убывающая функция).

Тогда наш пример \(\log_>(x)>\log_>График логарифма, основанного на 2, показан красным цветом. Синий — логарифм на основе 0,5

1. Необходимо привести логарифмы слева и справа к одинаковому основанию
2. Вычеркнуть логарифмы
3. Сохраняем знак неравенства, если основание больше единицы
4. Меняем знак неравенства на противоположный, если основание меньше 1
5. Внимательно следим за ОДЗ.

(4)\) решается правильно следующим образом: $ x 0\). Реакция: \(x\in(0;4)\).

Пример 1 $\log_(x)>3;$

Первым делом всегда записываем ОДЗ. Здесь оно достаточно простое: $x>0;$ Следующий шаг — сделать так, чтобы слева и справа стояли логарифмы с одинаковым основанием. Для этого представим число \(3\) в виде логарифма с основанием \(2\) по формуле, позволяющей представить любое число \(a\) в виде логарифма с нужным нам основанием \(b\): $a=\log_(b^a);$ $3=\log_(2^3);$ Подставим преобразования в исходное уравнение вместо тройки: $\log_(x)>\log_(2^3);$ Теперь у нас логарифмы с одинаковым основанием. Смотрим на это основание \(2>1\), значит просто избавляемся от логарифмов, оставляя знак неравенства прежним: $x>2^3;$ $x>8;$ Вспоминаем про найденный в начале примера ОДЗ и проверяем, чтобы все корни подходили. Это удобно сделать, отметив на оси \(х\) решение уравнения \(x>8\) и ОДЗ \(x>0\):

Метод замены переменной в неравенствах с логарифмом

Рассмотрим несколько примеров основных типов логарифмических неравенств.

Пример 5 $\log_^(x)+2>3\log_(x);$ Сперва найдем ОДЗ, здесь оно крайне простое: $x>0.$ Очень легкий пример, который решается при помощи замены. Действительно, обратите внимание, что логарифмы в неравенстве абсолютно одинаковые. Заменим их на какую-нибудь переменную \(t\): $Пусть \ t=\log_(x)$ Тогда неравенство примет вид: $t^2+2>3t;$ $t^2-3t+2>0;$ Получили обыкновенное квадратное неравенство, только относительно переменной не \(х\), а \(t\). Находим корни \(t\), раскладываем на множители и решаем методом интервалов: $(t-1)(t-2)>Еще один очень популярный тип неравенств — это неравенства, которые решаются путем замены переменной. Как всегда, проще объяснить это на примерах:

0;$ $t\in(-\infty;1)\cup(2;+\infty);$ То же самое можно переписать как набор неравенств, смысл останется тем же: $\left \begin t \lt 1, \t \gt 2. \end

ight.$ Не путайте набор с системой! Знак системы используется, когда вы хотите найти значения \(x\), которые ТОЧНО удовлетворяют всем неравенствам системы.

Знак кумуляты используется, когда необходимо объединить решения отдельных неравенств, т.е. решение кумулятивного неравенства является совокупностью корней каждого отдельного неравенства.

Итак, у нас совокупность из двух неравенств относительно переменной \(t\). Время сделать обратную замену — вместо \(t\) подставляем выражение, на которое мы его заменяли. Напоминаю \(t=\log_(x)\): $\left \begin \log_(x) \lt 1, \\ \log_(x) \gt 2. \\ \end \right.$ Ну вот, перед нами два простеньких логарифмических неравенства, которые мы уже научились решать выше: $\log_(x) $\log_(x)>2;$ $\log_(x)>\log_(3^2);$ $x>9.$ С учетом ОДЗ \((x>В данном примере мы используем совокупность, потому что нас устраивают оба \(t 2\). И то, и другое — решение проблемы неравенства.

Понимание разницы между агрегатом и системой является основополагающим для решения логарифмических и экспоненциальных неравенств. В данном примере мы знакомы с набором, а если используется система, то мы поговорим о ней чуть позже.<\log_<4>(64x)><\log_<4>(x)-3>0)\), и, не забывая о количестве, имеем: Ответ.<\log_<4>(x)-3><\log_<4>(64x)>Пример 6 $\frac<\log_<4>(x^4)+16><\log_<4>^(x)-9>+\frac

Запишем ОДЗ: $ \begin x>0, \\ \log_(x)-3\neq 0, \\ \log_(64x)\neq 0, \\ \log_^(x)-9 \neq 0. \end$ $ \begin x>0, \\ \log_(x)\neq \log_(4^3), \\ \log_(64x)\neq \log_(4^0), \\ (\log_(x)-3)(\log_(x)+3) \neq 0. \end$ $ \begin x>\geq\frac

.$ Неравенство на первый взгляд кажется немного пугающим. Но именно такой пример мы имели в США в 2017 году, и это совсем не страшно.

0, \\\\ \log_(x)

Сделаем обратную замену \(t=\log_(x)\): $\left \begin \log_(x) 3. \\ \end \right.$ Решаем получившиеся простенькие логарифмические неравенства и, неожиданно, одно уравнение. Обратите внимание, что мы решаем опять не систему, а совокупность. Нас устраивают все решения, полученные в каждом уравнении\неравенстве по отдельности. $\log_(x) $\log_(x)=1;$ $\log_(x)=\log_(4^1);$ $x=4.$ $\log_(x)>3;$ $\log_(x)>\log_(4^3);$ $x>eq \log_(4^3), \\\\ \log_(64x)

Основные положения и примеры решения простейших логарифмических неравенств.

eq \log_(4^0), \\\\ \log_(x)

К простейшим относятся логарифмические неравенства, которые содержат неизвестную переменную в составе аргумента логарифмической функции с фиксированным основанием, т.е. это неравенства вида \(log_a>\log_a\), где \(a>eq \log_(^).\end$ Отсюда следует, что ODE имеет вид.

Обратите внимание на точку \(t=1\), потому что при этом значении \(t\) все выражение равно нулю. В США очень часто встречаются отдельные моменты, о которых мы не должны забывать.

\left \begin t \l t-3, \left t=1, \ t \gt 3.\\\\ \endight.$числа \(x\) по основанию \(a\), где \(a>64.$

Обратите внимание логарифм определен только для положительных чисел. Соответственно, область определения логарифмической функции \(x \in (0;+\infty)\) или проще \(x>Этот раздел также открыт для студентов, желающих сдать экзамен по математике базового уровня. В тесте на пригодность есть и более сложные неравенства, но даже они так или иначе должны быть сведены к более простым.

0,\;a

Как уже упоминалось, логарифмическая функция монотонна. Посмотрите на её графики.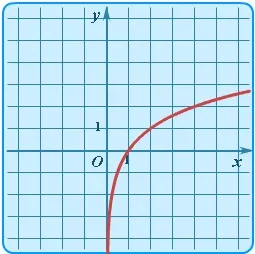

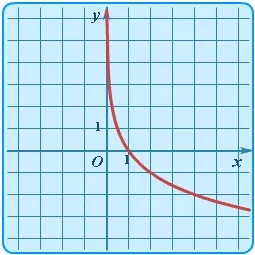
e1\) и неравенства, приведенные к этой форме. В более общих случаях неизвестная величина может также появляться в основании логарифма.

Чтобы решать как логарифмические неравенства, так и логарифмические уравнения, нам необходимо вспомнить определение и свойства логарифмической функции как таковой. 1) Логарифм — это трансцендентная функция, т.е. аналитическая функция, которая не может быть задана алгебраическим уравнением. Таким образом, чтобы получить решение простейшего логарифмического неравенства, мы должны сначала прибегнуть к алгебраическим соотношениям, то есть «вычесть» логарифм. 2) Логарифм является монотонной и монотонной функцией, что означает, что каждому значению аргумента из области определения соответствует только одно значение функции. Поэтому его можно сравнить с самим собой и «опустить» логарифм. Как и в каких случаях, мы объясним ниже на примерах. 3) Наиболее важным моментом является то, что логарифмическая функция имеет ограниченную область определения. Это означает, что при решении задач с логарифмами, содержащими переменные, нельзя забывать о ВЗП (диапазоне допустимых значений) этих переменных.

Логарифм

Область допустимых значений (ОДЗ) выражения \(2x+7>0.\)

Введение вспомогательной переменной

положительного

0,\- a

Логарифм

0.\)<2^>=\frac\log_2 = -\log_2\ Теперь неравенство имеет следующий вид \\log_2^2 — 7\log_2 +10>Область значений функции E = R — это множество действительных чисел. Это означает, что сам логарифм, в отличие от его аргумента и основания, может принимать любое значение в диапазоне \((-\infty; +\infty)\).

Поэтому для решения простейших логарифмических неравенств достаточно преобразовать обе части неравенства в логарифм с одинаковым основанием, а затем сравнить подлогарифмические выражения. Таким образом, мы сравниваем функцию с самой собой при разных значениях ее аргумента, то есть как будто «удаляем» логарифм с обеих сторон неравенства. Когда основание степени больше 1, знак неравенства без «log» совпадает со знаком исходного неравенства, что характерно для возрастающих функций — большему значению аргумента соответствует большее значение функции; когда основание степени меньше 1, знак неравенства противоположен знаку исходного неравенства, что характерно для убывающих функций — большему значению аргумента соответствует меньшее значение функции.

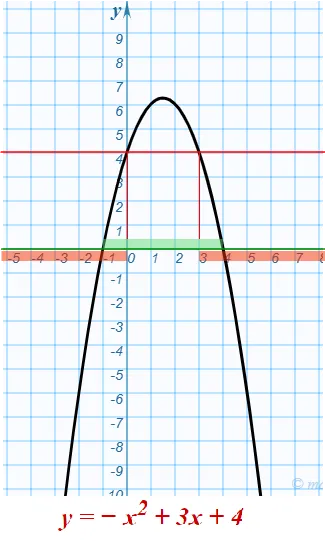
Пусть \(y = \log_2\), тогда логарифмическое неравенство преобразуется в обычное квадратное неравенство \y^2 — 7y +10>0,\ которое решается графически (через параболу) или методом интервалов. Сделайте это самостоятельно. Ответ получится такой \(y \in (-\infty;2)\cup(5;+\infty)\) или, что то же самое \\left \end>\right. \ Последняя запись удобнее для возврата от вспомогательной переменной к логарифму \\left \log_2 5. \end>\right.\ Имеем два простейших неравенства для логарифмов с основанием \(2>1\), решаем их \\log_2 5 \\ \log_2>\log_2 \\ 4+3x-x^2>Пример 1.<\left 4+3x-x^2>0,\\ 4+3x-x^2 0 ; \end>\right. \\ 4+3x-x^2>0,\\ 4+3x-x^2>32. \end>\left| x^2 -3x-4 3; \end>\right.>\end>\\ \end>\right.>Решение.<"), делаем окончательный вывод \(x \in (-1;0) \cup (3;4).\)

Для применения этого метода желательно обеспечить одинаковый вид логарифмических функций во всем неравенстве, поэтому при выполнении преобразований мы должны стремиться к одинаковым основаниям и логарифмическим аргументам. Давайте рассмотрим примеры.

Пример 4.

Решение.

Логарифм

Выпишем ОДЗ неравенства. Условие положительности всех аргументов логарифмической функции \\begin 64x>0;\\ x>0;\\ x^4>0 \end\ сводится к одному требованию \(x>

О разложении на множители

В последнем неравенстве неизвестная величина появляется в обеих суммах в совершенно одинаковой форме, поэтому мы можем продолжить решение, введя вспомогательную переменную.

\( \log_3\cdot\log_4 — \log_3 — \log_4 +1 0.\)\ \log_3\cdot\log_4 — \log_3 — \log_4 +1 0; \end>\\<\begin\log_4 - 1>0,\\ \log_3 — 1 1; \end>32. \ Два квадратичных неравенства, которые входят в уравнение (не забудьте!), образуют набор из двух наборов неравенств, которые при решении дают окончательный ответ. \<\log_4\log_3;>\end>\ Соединение множеств решений систем неравенств (обозначается скобками «») и пересечение множеств решений систем неравенств (обозначается скобками «»).<\begin\log_4>1,\\ \log_3 \log_4,\\ \log_3 3; \end>\; |\; \\<\beginx>Наблюдение 1. Чтобы не писать комбинации систем и системы множеств, особенно если вы запутались в этих скобках, можно изобразить все шаги решения с помощью диаграмм на числовой оси.

Наблюдение 2. Обратите внимание, что в какой-то момент решение задачи сводится к анализу неравенств, сравнивающих одну и ту же квадратичную тройку \(4+3x-x^2\) с числовыми значениями. Поэтому мы можем ограничиться построением одной параболы — эскиза графика функции \(y = 4+3x-x^2\) — и посмотреть, как она связана с горизонтальными линиями \(y = 0, \- y = 4\- и \- y = 32. \(Вспомните аналогичное задание в части 2 ЕГЭ 9 класса.) Это не займет много времени, потому что коэффициенты тринома — целые числа, корни легко вычисляются по теореме Виета, а параболу нужно построить только из характерных точек. Как быстро построить параболу, показано в обучающем видео на Youtube-канале Mathematichka.

ОДЗ: \(x>Ответ.<\log_3><\log_3<4>>Решение.

0\). Условие, что знаменатели всех дробей \begin \log_4-3

ОДЗ: \(x>e 0;\\\\ \log_4

e 0;\\\\ \log^2_4-9<\sqrt>e 0;\end\ записано пока формально, оно будет проанализировано в решении.<\sqrt>Метод разложения может быть применен ко всем типам неравенств, когда произведение этих коэффициентов сравнивается с нулем. Однако он не пользуется большим спросом для решения логарифмических неравенств из-за громоздких вычислений. Более того, те же неравенства обычно могут быть решены более компактно другими методами. Разложение на множители для выражений, содержащих логарифмы, чаще всего используется при решении уравнений. Поэтому метод факторизации можно сочетать с методом решения неравенств с помощью уравнений. Это возможно благодаря монотонности логарифмической функции. Давайте рассмотрим пример.<\sqrt>\; \left|||,<\sqrt>\Okay.<\sqrt>4,\\\\\ x 0\), мы можем записать ответ.<\sqrt>Решение II является вспомогательной переменной.<\sqrt>0. Приведем логарифмы к одному основанию, например, к основанию 3. \log_4 = \frac<\sqrt>)>.\ \\\\\log_3\cdot\log_4 — \log_3 — \log_4 +1 1.\) У нас \ 1 0\), поэтому это окончательный ответ.<\sqrt>1,\) то \(\log_4 3^1\; и\; 3>1,\) то \(\log_3>1.\) 3) пусть \(x = 9; \;x \in (4;+\infty)\) \\log_3\cdot\log_4 — \log_3 — \log_4 +1 = \\ = \log_3\cdot\log_4 — \log_3 — \log_4 +1 = \\ = 2\log_4 — 2 — \log_4 + 1 = \\ = \log_4 — 1>0, \ так как \(9>4^1\; и\; 4>1,\) то \(\log_4>Решение III дается уравнением.

0.\) Замените символ «

1) Пусть \(x = \sqrt \ca. 1.73? \;x \в (0;3)\), тогда \log_3\cdot\log_4 — \log_3 — \log_4 +1 = \log_3

\cdot\log_4

— \log_3

— \log_4

+1 = \\\\\\ = 0,5\log_4

Что такое ОДЗ? ОДЗ для логарифмических неравенств

— 0.5 — \log_4

+1 = \0.5 — 0.5\log_4

= 0,5(1 — \log_4

0,\ поскольку \(\sqrt 1,\) тогда \(\log_4

1.\)

Сформулируйте ответ, используя диаграмму.

Сравните все три решения этого не очень сложного неравенства и решите, какое из них подходит вам больше.

Внимание: Если вы обнаружили ошибку, пожалуйста, сообщите нам об этом по электронной почте.

Алгоритм решения логарифмического неравенства

Нравится ли вам материал на сайте? Узнайте, как вы можете поддержать сайт и помочь нам в его развитии.

• метод замены множителей;
• декомпозиции;
• метод рационализации.

Есть вопросы? Предложения? Контакт [email protected].

Предупреждение © mathematichka Прямое копирование материалов с других сайтов запрещено.

Аббревиатура обозначает диапазон допустимых значений. Нередко вопросы в США содержат такую формулировку. ODE полезен не только в логарифмических неравенствах.

Рекомендуется: Виды и примеры производной логарифма

Посмотрите еще раз на приведенный выше пример. Дальше мы рассмотрим ODE, чтобы вы поняли принцип и решение логарифмических неравенств не было лишним. Из определения логарифма следует, что 2x+4 должно быть больше нуля. В нашем случае это означает следующее.

По определению, это число должно быть положительным. Решите приведенное выше неравенство. Это можно сделать даже устно, здесь очевидно, что X не может быть меньше 2. Решением неравенства будет определение диапазона допустимых значений. Перейдем к решению более простого логарифмического неравенства.

Мы отбрасываем сами логарифмы из обеих частей неравенства. Что мы имеем в результате? Простое неравенство.

Решение проблемы не является сложным. X должно быть больше, че м-0,5. Теперь объедините эти два значения в систему. Например, вот так,

Это диапазон допустимых значений для данного логарифмического неравенства.

Зачем нам нужен ODE? Это возможность исключить неправильные и невозможные ответы. Если ответ не находится в диапазоне возможных значений, то ответ просто не имеет смысла. Это нужно запомнить надолго, потому что на ЕГЭ часто требуется найти EIR, и не только для логарифмических неравенств.

Решение состоит из нескольких шагов. Во-первых, необходимо определить диапазон допустимых значений. В УДЕ будет два значения, мы рассмотрели это выше. Затем нужно решить само неравенство. Методы решения могут быть следующими:

В зависимости от ситуации, возможно, стоит использовать один из вышеперечисленных методов. Давайте перейдем непосредственно к решению. Мы покажем вам наиболее распространенный метод, который подходит для решения задач ЕГЭ практически во всех случаях. Затем мы рассмотрим метод декомпозиции. Это может помочь вам, когда вы найдете особенно «трудное» неравенство. Алгоритм решения логарифмических неравенств.

Логарифмические неравенства с переменным основанием

Примеры решений :

Это неравенство досталось нам не бесплатно! Обратите внимание на основание. Помните, что если он больше единицы, то при поиске допустимого диапазона значений знак остается прежним; в противном случае нам придется изменить знак неравенства.

В результате получается неравенство:

Теперь сведем левую часть к форме уравнения, которая равна нулю. Вместо символа «меньше чем» вставляем «равно» и решаем уравнение. Таким образом, мы находим ODE. Надеюсь, у вас не возникнет проблем с решением такого простого уравнения. Ответы: -4 и-2. Это еще не все. Нам нужно построить эти точки на графике и пометить их знаками «+» и «-«. Что вам нужно сделать для достижения этой цели? Подставьте числа из пробелов в выражение. Для положительных значений добавьте «+».

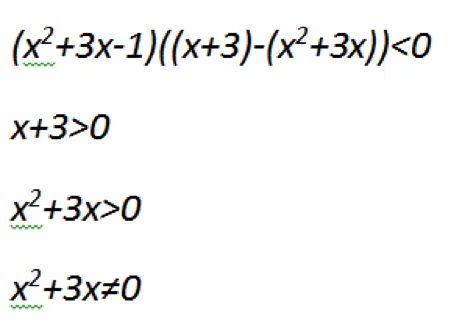
Ответ: x не может быть больш е-4 и меньш е-2.

Мы нашли диапазон допустимых значений только для левой стороны; теперь нам нужно найти диапазон допустимых значений для правой стороны. Это гораздо проще. Отве т-2. Мы пересекаем оба диапазона.

И только теперь мы начинаем решать само неравенство.

п.5. Примеры

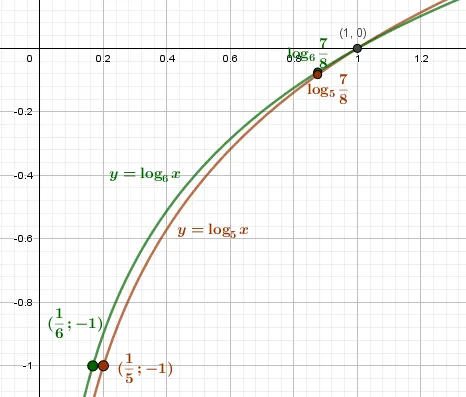
Максимально упростите задачу, чтобы ее было легче решить.<\lg\frac78><\lg 5>Снова применим метод интервалов к решению. Опустим расчеты, поскольку все уже ясно из предыдущего примера. Реакция.<\lg 7-\lg 8><\lg 5>Однако этот метод подходит, если логарифмическое неравенство имеет одинаковые основания.<\lg\frac78><\lg 6>Снова применим метод интервалов к решению. Опустим расчеты, поскольку все уже ясно из предыдущего примера. Реакция.<\lg 7-\lg 8><\lg 6>Как можно устранить это неравенство? Да, вы можете найти их в США. Решение неравенств следующим способом также окажет полезное влияние на ваше обучение. Давайте рассмотрим этот вопрос подробнее. Давайте оставим теорию в стороне и перейдем непосредственно к практике. Для решения логарифмических неравенств достаточно один раз ознакомиться с примером.<\lg 7-\lg 8><\lg 5>Рекомендуется: Определение и примеры неполных квадратных уравнений.<\lg 7\lg 8><\lg 6>Чтобы решить логарифмическое неравенство приведенного типа, необходимо правую часть привести к логарифму с тем же основанием. Принцип аналогичен принципу эквивалентных переходов. Следовательно, неравенство имеет следующий вид.<\lg 5>Рекомендуется: Определение и примеры неполных квадратных уравнений.<\lg 6>При использовании метода рационализации для решения неравенств необходимо помнить следующее: вычесть 1 из основания, вычесть x из обеих частей неравенства (справа налево) в соответствии с определением логарифма, перемножить два выражения и поставить их под первоначальным знаком относительно нуля.<\overbrace<(\lg 7-\lg8)>^<\lt 0>Дальнейшее решение осуществляется методом интервалов, который очень прост. Важно понимать различия в методах решения, тогда все будет работать легко.<(\lg 6-\lg 5)>^<\gt 0>><\underbrace<\lg 5\cdot\lg 6>_<\gt 0>>В логарифмических неравенствах есть много нюансов. Самые простые задачи решаются довольно легко. Как вы можете решить каждую из них без проблем? Вы уже получили все ответы в этой статье. Теперь у вас впереди много практики. Вы должны практиковаться в решении всех типов задач на экзамене, тогда вы получите наивысший балл. Удачи вам в вашем нелегком деле!

Пример 1: Сравнение чисел: a) \( a=\log_5\frac78,\ b=\log_6\frac78 \) Аналитический метод: \bgin a=\frac<\lg 11><\lg 5>=\frac<\lg 11><\lg 6>\lt 0,\ b=\frac<\lg 5>Рекомендуется: Определение и примеры неполных квадратных уравнений.<\lg 6>\{\lt 0\ a-b=\frac<\overbrace<\lg 11>^<\gt 0>Дальнейшее решение осуществляется методом интервалов, который очень прост. Важно понимать различия в методах решения, тогда все будет работать легко.<(\lg 6-\lg 5)>^<\gt 0>><\underbrace<\lg 5\cdot\lg 6>_<\gt 0>>=(\lg 7-\lg 8)\left(\frac

-\frac

\frac -\fright)\ a-b = \frac

\overbrace

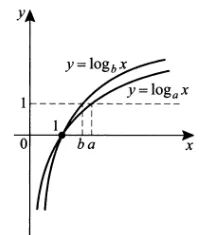
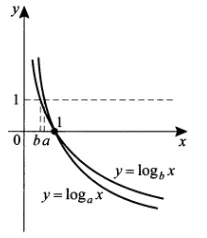
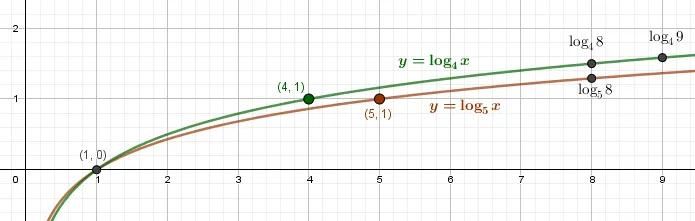
\lt 0\ a\lt b\end Графический метод: \(0\lt\frac78\lt 1\) С \(0\lt x\lt 1\) кривая \(\log_6x\gt\log_5x\) Таким образом, \(b\gt a\)<\log_7 x>б) \( a=\log_5 11,\ b=\log_6 11 \) Аналитическая процедура: \bgin a=\frac

{\frac,\ b=\frac<\log_4(4-9x)>\\\\\\{\a-b=\lg 11\left(\frac<\log_4(4-9x)>-\frac

ight)= \frac

Логарифмические уравнения и неравенства

\overbrace

\gt 0\a\gt b\end графический метод: \(11\gt 1\) С \(x\gt 1\) кривая \(\log_5x\gt\log_6x\) Так \(a\gt b\)

Логарифмическая функция

Определение

д*) \( a=\log_2 3,\ b=\log_5 8 \) Преобразование и графическое решение: $ a=\log_2 3=\log_4 9\gt\log_4 8\gt\log_5 8=b $ $ a\gt b

Основные свойства

Пример 2*. Решите неравенство: a) \( \log_(x^2-7x)\geq\log_(3x+11)\) \begin \begin x^2-7x\leq 3x+11\ x^2-7x\gt 0\\\\ 3x+11\gt 0\end_aightarrow 0\lt x^2-7x\leq 3x+11

	a>1	0
ightarrow \begin x^2-7x\leq 3x+11\ x^2- 7x\gt \end	ightarrow \begin x^2-… 10x-11\leq 0\leq 0\\\\ x(x-7)\gt 0 \end \стрелка вправо \begin (x+1)(x-11)\leq 0\leq 0\gt 0\end \end \end \end \(-1\leq x\leq 0\cup 7\lt x\leq 11\) ответ: \(x\in\left. \cup\left.\left(7;11	ightarrow \begin x^2-… 10x-11\leq 0\leq 0\\\\ x(x-7)\gt 0 \end \стрелка вправо \begin (x+1)(x-11)\leq 0\leq 0\gt 0\end \end \end \end \(-1\leq x\leq 0\cup 7\lt x\leq 11\) ответ: \(x\in\left. \cup\left.\left(7;11
ight\)	b) \( \log_3x+\log_3(x-8)\geq 2 \) \begin \log_3\left(x(x-8)	b) \( \log_3x+\log_3(x-8)\geq 2 \) \begin \log_3\left(x(x-8)
ight.	ight\)	c) \( \frac
\gt 0 \) Дробь положительна, если числитель и знаменатель имеют одинаковый знак. Мы получаем набор. \ стрелка вправо \ стрелка влево \топ \топ \топ x\gt-1.5\x1\gt-1\gt-1\gt-1\gt-1\gt-1\gt-0 \end \топ x\lt-1.5\gt-1\gt-1\gt-1\gt-1\gt-0 \end \end \end \end \end \end \end \end \end \end \end. Стрелка вправо x\gt 1 \ конец \ конец \ конец \ конец \ конец ответ: \(x\in(1;+\infty)\)	\lt 16 \) Конверсия: \(4^(4^(4^(4^))	\lt 16 \) Конверсия: \(4^(4^(4^(4^))
д) \( \lg^2x+\lg x\gt 2\) ODD: \(x\lt 0\) Заменить: \(t=\lg x\) \(t^2+t-2\gt 0\) Стрелка вправо (t+2)(t-1)\gt 0\) \(t\l t-2\cup t\gt 1\) Возврат к исходной переменной: \start \lg x\l t-2\cup\lg x\gt 1	ight arrow \start x\lt 10^\cup x\gt 10\\\\\ x\gt 0\end	ight arrow 0\lt x\lt 0.01\cup x\gt 10 \end Ответ: \(x\in(0;0.01)\cup(10;+\infty)\)

График логарифмической функции

Логарифмические уравнения и неравенства в вариантах математики GCSE рассматриваются в задании C3. Каждый ученик должен научиться решать задачи C3 на экзамене по математике GCSE, если он хочет сдать экзамен на «хорошо» или «отлично». В этой статье дается краткий обзор распространенных логарифмических уравнений и неравенств и основных методов их решения.

Свойства логарифмов

Поэтому сегодня мы рассмотрим некоторые примеры логарифмических уравнений и неравенств, которые задавались учащимся в тестах ЕГЭ по математике в предыдущие годы. Однако мы начнем с краткого описания основных теоретических положений, необходимых для их решения.

0,\, c>0,\, a\ne 1. \» width=»439″ height=»20″ />

называется логарифмической функцией.

0,\, c>0,\, a\ne 1. \» width=»435″ height=»41″ />

Основные свойства логарифмической функции y = log

0,\, a\ne 1. \» width=»322″ height=»20″ />

x :

0,\, c>0,\, a\ne 1,\, c\ne 1. \» width=»421″ height=»46″ />

Решение логарифмических уравнений и неравенств

Диапазон определения

D ( f ) = (0; +∞)

0 \end\Leftrightarrow \beginx^2>6, \\ x>-1,6. \end\Leftrightarrow \» width=»316″ height=»60″ />

D ( f ) = (0; +∞)

Диапазон значений

E ( f ) = (-∞; +∞)

E ( f ) = (-∞; +∞)

Монотонность

Увеличивается на (0; +∞)

Уменьшается на (0; +∞)

0 \end\Leftrightarrow \begin-1

Следующий

Непрерывный

Непрерывный

Выпуклый

Решение. Область допустимых значений уравнения определяется здесь легко: x>Изогнутый вверх

Изогнутые вниз

Логарифмирование уравнений

График логарифмической функции — это логарифмическая кривая:

— Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

— Логарифм произведения двух положительных чисел равен разности логарифмов этих чисел:

— Если a и b — положительные числа и a ≠ 1, то для каждого числа r верно равенство:

Переход от логарифмических неравенств к нелогарифмическим

— Если a, b, c — положительные числа и a и c отличны от единицы, то верно равенство (формула перехода к новому основанию логарифма):_ax при условии а>Пример 1. Решите уравнение:aРешение. Диапазон допустимых значений включает только те значения x, при которых выражение под логарифмом больше нуля. Эти значения определяются следующей системой неравенств:_aУчитывая, что_aполучаем интервал, определяющий диапазон допустимых значений логарифмического уравнения:_aНачиная с Теоремы 1, все условия которой здесь выполняются, мы получаем следующее эквивалентное квадратичное уравнение:_atas:

В диапазон допустимых значений входит только первый корень._ataОтвет: x = 7.

Пример 2. Решите уравнение:

Решение. Диапазон допустимых значений уравнения определяется системой неравенств:

Очевидно, что эти два условия противоречат друг другу. То есть не существует значения x, для которого оба неравенства выполняются одновременно. Область допустимых значений уравнения является пустым множеством, что означает, что логарифмическое уравнение не имеет решений.

Ответ: Корней нет.

Обратите внимание, что в этой задаче нам совсем не нужно было искать корни уравнения. Достаточно было определить, что допустимый диапазон значений не содержит ни одного действительного числа. Это одно из преимуществ данной последовательности при решении логарифмических уравнений и неравенств (мы начинаем с определения диапазона допустимых значений уравнения, а затем решаем его с помощью преобразований уравнений).<29 справедливо в любом случае:

Пример 3. Решите уравнение:0.Уравнение имеет вид:_aЕсли логарифмы получены из одинаковых значений по одному и тому же основанию, то они, очевидно, равны. Если подобный прием используется при решении уравнения, то выполняется логарифмирование уравнения. Иногда логарифмы используются для решения очень сложных примеров._at>Задача. Определите корни уравнения_as:

Переменная является одновременно основанием степени и ее экспонентой. Возьмите из левой и правой частей уравнения логарифм по основанию 5:t>Задача. Определите корни уравнения_aИсследуйте график логарифмической функции y = log

Это возрастающая функция. Если отложить на оси Ох два числа t и s так, чтобы t находилось слева от s (т.е. t

Ответ: Корней нет.

Ответ: Корней нет.

Неравенства вида log_ax

t меньше, чем log

Ответ: Корней нет.

Из рисунка можно сделать вывод, что неравенства log₄s и t 1). Однако это не совсем верно. Мы также должны учитывать, что под знаком логарифма может быть только одно положительное число. Оказывается, что простейшее логарифмическое неравенство имеет вид

Ответ: Корней нет.

Задача. Найдите решение логарифмического неравенства

Логарифмические неравенства

Ответ также может быть дан в этой форме, но обычно его записывают в виде бланка. Очевидно, что неравенство равно 0.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Проблема. Решите это неравенство.

Очевидно, что первую часть этого двойного неравенства можно просто отбросить, поскольку условие 0.

3. Смотрите статистику просмотра видеоуроков учениками.

Конспект урока «Логарифмические неравенства»

Условие немного меняется, когда логарифмическая основа меньше единицы, т.е. 0 a

x больше не увеличивается, а уменьшается. Если затем мы отметим точку на оси O x t, которая ta

t выше по оси O, чем log

s, т.е. log

журнал

Но опять же, мы должны помнить, что t может быть только положительным (тогда s, которое больше t, автоматически положительно). Видно, что при 0a

журнал

s, мы можем свести к двойному неэквиваленту 0.

Грубо говоря, при переходе от логарифмического уравнения к нелогарифмическому знак неравенства сохраняется, если отношение логарифма к основанию больше единицы. В противном случае знак неравенства меняется на противоположный.

Работа. Решите неравенство

Задание. Решите неравенство.

Если одна часть неравенства содержит логарифм, а другая — простое число, просто замените логарифм на число, чтобы свести его к известным неравенствам.

Задание. Решите неравенство
Представьте 0,5 в виде логарифма по основанию 4. Поскольку 0,5 = log

2, уравнение можно переписать следующим образом:

Задание. Решите неравенство.

Задание. Решите неравенство.

В этом видеоуроке мы вспомним, какая функция называется логарифмической и какими свойствами обладает логарифмическая функция. Мы научимся решать логарифмические неравенства.
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам необходимо добавить его в свой личный кабинет.
2. Распределите видеоуроки по личным кабинетам ваших учеников.

Помните: логарифмическая функция — это функция вида — заданное число, .

Задание. Решите неравенство
1. логарифмическая функция определяется множеством всех положительных чисел.

2: Множество значений логарифмической функции — это множество всех положительных чисел.

3. логарифмическая функция не ограничена.
4. он увеличивается в интервале, и уменьшается в интервале .

5. если, и ее значения в отрицательны, то, напротив, функция имеет положительные значения в, а ее отрицательные значения в
Теперь мы хотим научиться решать логарифмические неравенства.

Разве мы не знаем, как их решить? Когда мы рассматривали логарифмическую функцию, мы рассматривали неравенства вида: .

Например, неравенство, в виде логарифма имеет вид: .

Мы только что вспомнили свойства логарифмической функции и можем сказать, что функция и является возрастающей, так как она имеет вид .
Нарисуем множество решений на координатной прямой. Мы показываем точки как «нарисованные», потому что наши неравенства строгие.
Мы видим, что общий интервал является интервалом of, поэтому решением исходного неравенства является
Какие неравенства мы будем решать сегодня? На сегодняшнем уроке мы будем решать неравенства вида:

Решение логарифмических неравенств основано на свойстве возрастания и убывания логарифмических функций.