Определение. Функция надежности R(t) — это функция, определяющая вероятность того, что устройство выйдет из строя в момент времени t.
Основные законы распределения
Биномиальный закон распределения описывает вероятность того, что событие A произойдет m раз в n независимых испытаниях, при условии, что вероятность p того, что событие A произойдет в каждом испытании, постоянна.
Например, в отделе продаж магазина бытовой техники заказ на телевизор поступает в среднем каждые 10 звонков. Постройте закон распределения вероятностей для покупки m телевизоров. Постройте многоугольник распределения вероятности.
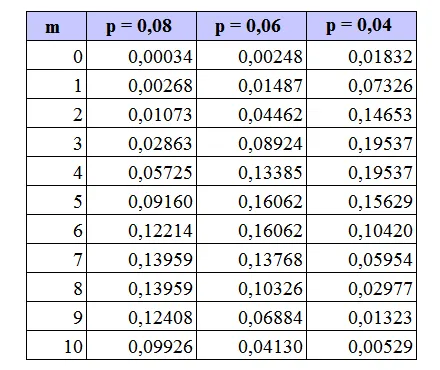
В таблице m — это количество заказов, полученных компанией на покупку телевизора. Сnm — число комбинаций из m телевизоров в n; p — вероятность события A, т.е. заказа телевизора; q — вероятность того, что событие A не произойдет, т.е. не будет заказан телевизор; P m,n — вероятность заказа m телевизоров из n. На рисунке 1 показан многоугольник распределения вероятностей.
Геометрическое распределение.
Геометрическое распределение случайной величины выглядит следующим образом:
P m — вероятность наступления события A в испытании с номером m. p — вероятность наступления события A в испытании. q = 1 — p
Пример. Компания по ремонту бытовой техники получила партию из 10 запасных частей для стиральных машин. Случается, что 1 изделие из партии оказывается бракованным. Перед тем как найти неисправный прибор, проводится проверка. Необходимо определить закон распределения для количества тестируемых единиц. Вероятность того, что прибор неисправен, равна 0,1. Постройте многоугольник для распределения вероятности.
Из таблицы видно, что с увеличением числа m вероятность найти дефектную единицу уменьшается. Последний ряд (m=10) связывает две вероятности: 1 — что десятый прибор оказался бракованным — 0,038742049, 2 — что все испытанные приборы исправны — 0,34867844. Поскольку вероятность того, что прибор бракованный, относительно мала (p=0,1), вероятность последнего события P m (10 испытанных приборов) относительно велика. Рисунок 2.
Гипергеометрическое распределение.
Гипергеометрическое распределение случайной величины выглядит следующим образом:
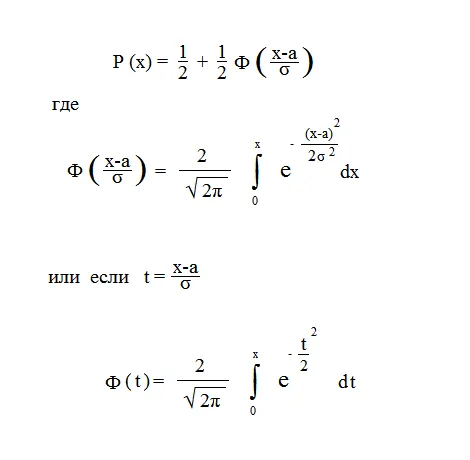
Например, постройте закон распределения 7 угаданных чисел из 49. В этом примере множество чисел N = 49, изъято n = 7 чисел, M — множество чисел, обладающих определенным свойством, т.е. правильно угаданных чисел, m — количество правильно угаданных чисел среди изъятых.
Из таблицы видно, что вероятность угадать число m = 1 выше, чем для m = 0. После этого, однако, вероятность быстро уменьшается. Таким образом, вероятность угадать 4 числа уже меньше 0,005, в то время как вероятность угадать 5 чисел ничтожно мала.
Равномерный и показательный законы распределения непрерывной случайной величины
Мы объясняем законы равномерного распределения и экспоненциального распределения, формулы вероятности и числовые характеристики этих функций.
Задача 1.
Автобусы ходят строго по расписанию. Интервал между ними составляет 7 минут. Найдите: (a) вероятность того, что пассажир, прибывший на остановку, будет ждать автобус менее двух минут. (b) вероятность того, что пассажир, прибывший на остановку, будет ждать автобус не менее трех минут. (c) ожидаемое значение и стандартное отклонение случайной величины X — времени ожидания пассажира.
Решение.1. согласно задаче, непрерывная случайная величина X= равномерно распределена между прибытиями двух автобусов. Длина интервала распределения случайной величины X равна b-a=7, где a=0, b=7.
2. время ожидания меньше двух минут, если случайная переменная X попадает в интервал (5;7). Вероятность того, что она попадает в интервал, можно рассчитать по следующей формуле: P(x12)=(х2-х1)/(b-a). Р(5<Х<7) = (7-5)/(7-0) = 2/7 ≈ 0,286.
3. время ожидания составляет не менее трех минут (т.е. от трех до семи минут), если случайная переменная X попадает в интервал (0;4). Вероятность того, что он попадает в интервал, мы определяем по следующей формуле: P(x12)=(х2-х1)/(b-a). Р(0<Х<4) = (4-0)/(7-0) = 4/7 ≈ 0,571.
4. математическое ожидаемое значение непрерывной равномерно распределенной случайной величины X — времени ожидания пассажира — определяется по следующей формуле: M(x)=(a+b)/2. M(X) = (0+7)/2 = 7/2 = 3,5.
5. среднеквадратичное отклонение непрерывной, равномерно распределенной случайной величины X, времени ожидания пассажира, рассчитывается по формуле: σ(X)=√D=(b-a)/2√3. σ(X)=(7-0)/2√3=7/2√3≈2,02.
Задача 2.
Экспоненциальное распределение задается плотностью f(x) = 5e — 5x для x ≥ 0. Вам необходимо: a) написать выражение для функции распределения; b) найти вероятность того, что x попадает в интервал (1;4); c) найти вероятность того, что x ≥ 2- d) оценить M(x), D(x), σ(x).
Решение.1. поскольку по условию дано экспоненциальное распределение, формула для плотности распределения вероятности случайной величины дает X λ = 5. тогда функция распределения будет иметь вид:
 |
2. вероятность того, что в результате испытания X попадет в интервал (1;4), находим по формуле P(a 4. мы находим его для экспоненциального распределения: Список использованных источников Определение. Нормальное распределение — это распределение вероятностей непрерывной случайной величины, заданное функцией плотности вероятности Закон нормального распределения также известен как закон Гаусса. Закон нормального распределения является центральным элементом теории вероятностей. Это происходит потому, что случайная величина всегда является результатом воздействия большого числа различных факторов. Все другие законы распределения являются приближением к нормальному закону. Можно легко показать, что параметры и, которые содержатся в плотности распределения, являются математическим ожиданием и стандартным отклонением случайной величины X, соответственно. Найдем функцию распределения F(x) . График плотности нормального распределения называется нормальной кривой или кривой Гаусса. 1 ) Функция определена на целочисленной оси. 2 ) Для всех x функция распределения имеет только положительные значения. 3 ) Ось OH является горизонтальной асимптотой графика функции плотности вероятности, поскольку если абсолютное значение x неограниченно возрастает, то значение функции стремится к нулю. 4 ) Мы хотим найти точку экстремума функции. Т.к. при y’>0 при x 5 ) Функция симметрична относительно прямой x = a, так как разность ( x — a ) является квадратичной функцией плотности. 6 ) Чтобы найти поворотные точки графика, необходимо определить вторую производную функции плотности. В точках x = m + s и x = m — s вторая производная равна нулю и меняет знак при прохождении через эти точки, т.е. функция имеет кривую в этих точках. В этих точках значение функции равно . 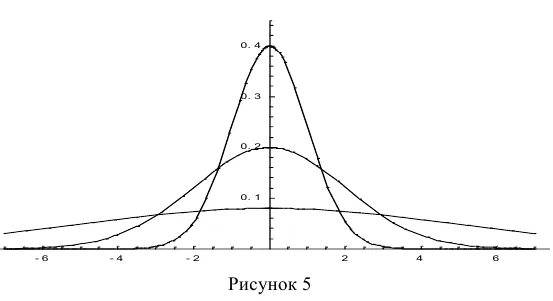Мы хотим построить график функции плотности. Мы построили графики для t = 0 и трех возможных значений стандартного отклонения s = 1, s = 2 и s = 7. Как видите, график становится более плоским по мере увеличения значения стандартного отклонения и уменьшения максимального значения. Если а>0, график смещается в положительном направлении, когда a<0 – в отрицательном. Когда a = 0 и s = 1, график считается нормализованным. 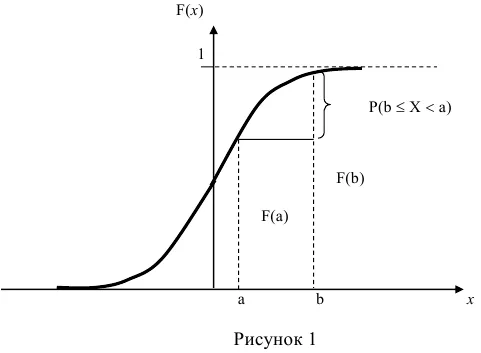Уравнение нормализованной кривой: Определим вероятность того, что случайная величина, распределенная по нормальному закону, попадает в определенный интервал. Поскольку интеграл не выражается в терминах элементарных функций, мы выполняем функцию которая называется функцией Лапласа или интегралом вероятности. Значения этой функции для различных значений x вычисляются и приводятся в специальных таблицах. Ниже показан график функции Лапласа. Функция Лапласа также называется функцией ошибки и обозначается erf x. Также используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением: График нормализованной функции Лапласа показан ниже. Рекомендуемое чтение: Влияние физико-климатических условий на архитектурно-дизайнерские решения жилых зданий Характеристика проектирования жилых зданий в различных физико-климатических условиях. Понятие иска и его элементы. Виды исков Иск в гражданском процессе — это иск, поданный в суд заинтересованным лицом для защиты потерпевшего или пострадавшего. Классификация стратегий преодоления Вопрос эффективного и неэффективного преодоления напрямую связан с понятием стратегий преодоления. Юридическая техника: понятие, виды Юридическая техника — это совокупность правил, средств и приемов подготовки, принятия и формирования нормативных правовых актов. Компонентами психологической готовности являются: (выберите один) a) психическая готовность b) личностная готовность c) социально-психологическая готовность d) поведенческая готовность. Всегда опирайтесь на мысль о том, что ваше собственное решение добиться успеха намного важнее всего другого. © Авраам Линкольн ==>прочитайте все объяснения. 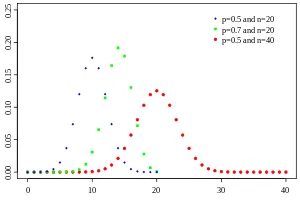Количество успехов в испытаниях, результаты которых распределены по вероятности Бернулли (пример с возвращением мячей в корзину), описывается биномиальным распределением: Здесь число комбинаций из . Другими словами, биномиальное распределение описывает сумму независимых случайных величин, которые имеют распределение Бернулли с вероятностью успеха. Ожидание и дисперсия: Биномиальное распределение справедливо только для обратной выборки, т.е. если вероятность успеха остается постоянной для всей серии тестов. Если множества и и имеют биномиальное распределение с параметрами и, то их сумма также имеет биномиальное распределение с параметрами . Представим себе ситуацию, когда мы достаем шары из корзины и возвращаем их до тех пор, пока не достанем белый шар. Количество этих операций описывается геометрическим распределением. Другими словами, геометрическое распределение описывает количество попыток до первого успеха с вероятностью успеха при каждой попытке. Если подразумевается количество попыток, в которых успех был достигнут, то геометрическое распределение описывается следующей формулой: Ожидаемое значение и дисперсия геометрического распределения: Геометрическое распределение генетически связано с экспоненциальным распределением, которое описывает непрерывную случайную величину: время до наступления события с постоянной скоростью наступления событий. Геометрическое распределение также является частным случаем отрицательного биномиального распределения. Распределение Паскаля является обобщением геометрического распределения: оно описывает распределение числа неудач в независимых испытаниях, результаты которых распределены по Бернулли с вероятностью успеха перед успехами в сумме. По, мы получаем геометрическое распределение для значения . Здесь число комбинаций из . Ожидаемое значение и дисперсия отрицательного биномиального распределения: Сумма независимых случайных величин, распределенных по Паскалю, также распределена по Паскалю: Предположим, что он имеет распределение, и -. Если они также независимы, то их сумма имеет распределение
Другие статьи по данной теме:
9 Нормальный закон распределения
Нормальная кривая обладает следующими свойствами:
10 Функция Лапласа
Функция Лапласа обладает следующими свойствами:
Биномиальное распределение
Геометрическое распределение
Распределение Паскаля (отрицательное биномиальное рспределение)
