Иногда встречаются выражения с большим количеством скобок. В этих примерах раскрытие скобок и нанизывание похожих скобок друг на друга происходит последовательно, с учетом всех существующих правил.
Раскрытие скобок
Мы продолжаем изучать основы алгебры. В этом уроке мы узнаем, как раскрывать круглые скобки в выражениях. Раскрыть круглые скобки означает избавиться от круглых скобок.
Чтобы раскрыть круглые скобки, нам нужно запомнить два правила. При регулярной практике вы сможете раскрывать круглые скобки с закрытыми глазами, и можете смело забыть эти заученные правила.
Первое правило раскрытия скобок
Рассмотрим следующее выражение:
Значение этого выражения равно 2. Выражение заключено в раскрытые круглые скобки. Раскрытие круглых скобок означает удаление скобок без изменения значения выражения. Таким образом, значение 8 + (-9 + 3) после удаления скобок должно быть равно 2.
Первое правило для раскрытия скобок следующее:
Если перед скобкой стоит знак плюс, то знак плюс удаляется вместе со скобкой.
Итак, мы видим, что в выражении 8 + (-9 + 3) перед скобкой стоит плюс. Этот плюс должен быть опущен вместе со скобками. Другими словами, скобки исчезают вместе с предшествующим знаком плюс. А то, что было в скобках, написано без изменений:

У нас есть выражение без скобок 8-9+3. Это выражение равно 2, так же как и предыдущее выражение со скобками равно 2.
Поэтому выражения 8+(-9+3) и 8-9+3 можно приравнять, так как они имеют одинаковое значение:
8 + (-9 + 3) = 8 — 9 + 3
Пример 2: Открытые скобки в выражении 3 + (-1 — 4)
Перед скобкой стоит знак плюс, поэтому этот знак плюс опускается вместе со скобкой. То, что было в скобках, остается неизменным:
3 + (-1 — 4) = 3 — 1 — 4
Пример 3: Открытые скобки в выражении 2 + (-1)
Перед скобкой стоит знак плюс, поэтому этот знак плюс опускается вместе со скобкой. То, что было в скобках, остается неизменным:
В этом примере раскрытие скобок становится своего рода обратной операцией, заменяющей вычитание сложением. Что это значит?
В выражении 2 — 1 есть вычитание, но его можно заменить сложением. Получаем 2 + (-1). Но если раскрыть скобки в 2 + (-1), то получится исходное 2 — 1.
Таким образом, первое правило раскрытия скобок можно использовать для упрощения выражений после любого преобразования. Можно опустить круглые скобки и сделать это проще.
Чтобы упростить данное выражение, мы можем складывать подобные суммы. Помните, что для уменьшения подобной суммы нужно сложить квадрат подобных сумм и умножить результат на общую часть буквы:
![]()
Получаем выражение 3 a + (-4 b ), в котором раскрываем скобки. Перед скобками стоит знак плюс. Поэтому мы применяем первое правило для открывающих скобок, то есть оставляем скобки вместе со знаком плюс перед скобкой:
Поэтому выражение 2 a+a- 5 b+b упрощается до 3 a- 4 b.
Если мы откроем несколько скобок, их может быть больше. Применяются те же правила, что и раньше. Например, раскройте круглые скобки в следующем выражении:
Есть два места, где необходимо открыть скобы. В этом случае применяется первое правило раскрытия скобок, то есть скобка удаляется вместе со знаком плюс перед скобкой:
2 + (-3 + 1) + 3 + (-6) = 2 — 3 + 1 + 3 — 6
Пример 3: Открытые скобки в выражении 6+(-3)+(-2)
В обоих местах, где появляются круглые скобки, перед скобками стоит знак плюс. Первое правило расширения скобок применимо и здесь:
Второе правило раскрытия скобок
Теперь рассмотрим второе правило в скобках. Он применяется, когда скобкам предшествует знак минус.
Если перед скобками стоит минус, то минус удаляется вместе со скобками, но суммы, которые были в скобках, меняют свой знак на противоположный.
Например, раскроем круглые скобки в следующем выражении
Мы видим, что перед скобками стоит знак минус. Поэтому мы должны применить второе правило, то есть оставить скобки со знаком минус перед ними. В этом случае суммы в скобках меняют свой знак на противоположный:

Получаем выражение без скобок 5 + 2 + 3. Это выражение равно 10, так же как предыдущее выражение со скобками было равно 10.
Поэтому выражения 5-(-2-3) и 5+2+3 можно приравнять, так как они имеют одинаковое значение:
5 — (-2 — 3) = 5 + 2 + 3
Пример 2: Раскрыть скобки в выражении 6 — (-2 — 5).
Мы используем второе правило для открывающих скобок, т.е. оставляем скобки и знак минус перед ними. В этом случае мы пишем сумму в скобках с обратным знаком:
6 — (-2 — 5) = 6 + 2 + 5
Пример 3: Открытые скобки в выражении 2 — (7 + 3)
Перед скобкой стоит знак минус, поэтому мы применим второе правило для раскрытия скобок:
2 — (7 + 3) = 2 — 7 — 3
Пример 4: Раскрытые круглые скобки в выражении -(-3 + 4)
Перед скобкой стоит знак минус, поэтому мы применим второе правило для раскрытия скобок:
Пример 5. Раскрыть скобки в выражении -(-8 — 2) + 16 + (-9 — 2).
Есть два места, где необходимо открыть скобки. В первом случае действует второе правило раскрытия скобок, а для выражения +(-9 — 2) действует первое правило:
-(-8 — 2) + 16 + (-9 — 2) = 8 + 2 + 16 — 9 — 2
Пример 6: Открытые скобки в выражении -(-a — 1)
Перед скобкой стоит знак минус, поэтому мы применим второе правило для раскрытия скобок:
Пример 7. Раскройте скобки в выражении -(4a + 3).
Перед скобкой стоит знак минус, поэтому мы применим второе правило для раскрытия скобок:
Пример 8. Раскройте скобки в выражении a -(4b + 3) + 15.
Перед скобкой стоит знак минус, поэтому мы применим второе правило для раскрытия скобок:
Пример 9. Раскройте скобки в выражении 2a + (3b — b) — (3c + 5).
Есть два места, где необходимо открыть скобки. В первом случае действует первое правило раскрытия скобок, а в выражении -(3c + 5) действует второе правило:
2a + (3b — b) — (3c + 5) = 2a + 3b — b — 3c — 5.
Пример 10. Открытые скобки в выражени и-a — (-4a) + (-6b) — (-8c + 15)
В трех местах скобки необходимо расширить. Сначала примените второе правило для расширения скобок, затем первое, а затем снова второе:
-a — (-4a) + (-6b) — (-8c + 15) = -a + 4a — 6b + 8c — 15
Как раскрывать скобки в выражениях и уравнениях. Правила математики.
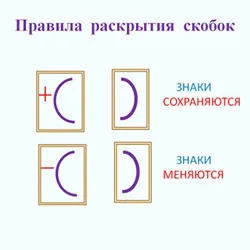
Круглые скобки используются для указания порядка операций в числовых и литературных выражениях, а также в выражениях с переменными. Удобно переходить от выражения со скобками к эквивалентному выражению без скобок. Эта техника называется расширением брекетов.
Раскрыть круглые скобки означает избавиться от скобок.
Еще один момент, требующий особого внимания, — особенности написания решений при раскрытии скобок. Мы можем записать исходное выражение со скобками и результат после раскрытия скобок в виде равенства. Например, раскрыв скобки, мы получим 3-5+7 вместо 3-(5-7). Мы можем записать эти два выражения как равные 3-(5-7)=3-5+7.
Еще один важный момент. В математике принято не писать знак плюс, когда он стоит в начале выражения или в скобках для сокращения записи. Например, если мы складываем два положительных числа, например, семь и три, мы не пишем +7+3, а просто 7+3, хотя семь — тоже положительное число. Это аналогично выражению (5+x): Перед скобкой стоит плюс, который не пишется, а перед пятеркой стоит плюс +(+5+x).
Правило раскрытия скобок при вычитании
Если перед скобкой стоит минус, то этот минус удаляется вместе со скобкой, но суммы, которые были в скобке, меняют свой знак на противоположный. Отсутствие знака перед первым слагаемым в круглых скобках означает знак +.
Пример. Открытые скобки в выражении 2 — (7 + 3)
Нам нужно изменить знак перед скобками, то есть изменить знак перед числами в скобках. Перед 7 в скобках нет знака, что означает, что число 7 является положительным и поэтому рассматривается как знак плюс перед ним.
2 — (7 + 3) = 2 — (+ 7 + 3)
Когда мы раскрываем скобки, мы убираем знак минус перед скобкой и сами скобки 2 — ( + 7 + 3 ), и меняем символы, которые были в скобках, на противоположные.
2 — (+ 7 + 3) = 2 — 7 — 3
Раскрытие скобок при умножении
Если перед скобкой стоит символ умножения, то каждое число в скобке умножается на множитель, стоящий перед скобкой. Умножение минуса на минус дает плюс, умножение минуса на плюс и умножение плюса на минус дает минус.
Таким образом, скобки в произведениях развиваются в соответствии с распределительным свойством умножения.
Пример. 2 — (9 — 7) = 2 — 9 — 2 — 7
Когда скобка умножается на скобку, каждый член первой скобки умножается на каждый член второй скобки.
(2 + 3) — (4 + 5) = 2 — 4 + 2 — 5 + 3 — 4 + 3 — 5
Вам не нужно запоминать все правила, достаточно одного: c(a-b)=ca-cb. Почему? Потому что если вы замените c на единицу, то получите правило (a-b)=a-b. А если подставить минус единицу, то получится правило -(a-b)=-a+b. Ну, а если вы замените c на другую скобку, то получите последнее правило.
Правило раскрытия скобок при вычитании
Если перед скобкой стоит знак минус, то скобка опускается, а сумма внутри скобки меняет свой знак на противоположный. Например: -(a-b) = -a+b
Пример 1: 8-(5-3) = 6. Ответ. Пример 2: 6 — (-1 + 2) = 5. Ответ: 6 + 1 — 2 = 5. Пример 3: 8a-(3b — 6a). Ответ: 8a — 3b + 6a = 14a — 3b. Пример 4: — (5 b-2). Ответ: -5b +2.
Раскрытие скобок при умножении
Если перед скобкой стоит знак умножения, то каждое число в скобке умножается на множитель, стоящий перед скобкой. Умножение минуса на минус дает плюс, а умножение минуса на плюс дает минус. Это правило основано на распределительном законе умножения: a(b+c) = ab + ac.
Пример 1: 8 × (5 — 3) = 16. Ответ: 8 ×5 — 8 ×3 = 16. Пример 2: a × (7 + 2). Ответ: a×7+a×2 = 7a + 2a = 9a. Пример 3: 8×(3 b-6a). Ответ: 8×3b — 8×6a = 24b — 48a.
Раскрытие скобок при умножении двух скобок
Когда скобка умножается на скобку, каждая сумма первой скобки умножается на каждую сумму второй скобки. Например: (c+d) × (a-b) = c×(a-b)+d×(a-b) = ca-cb+da-db.
Пример. Раскрытые скобки: (2-а) × (3-а-1). Решение: Шаг 1. Вычтите первую скобку (умножьте каждую сумму на вторую скобку): 2 × (3a-1) — a × (3a-1). Шаг 2. Разложите произведение скобок: (2×3a- 2×1) — (a×3a-a×1) = 2×3a- 2×1 — a×3a + a×1. Шаг 3. Перемножьте и сложите подобные члены: 6a-2-3a2+a = 7a-2-3a2








