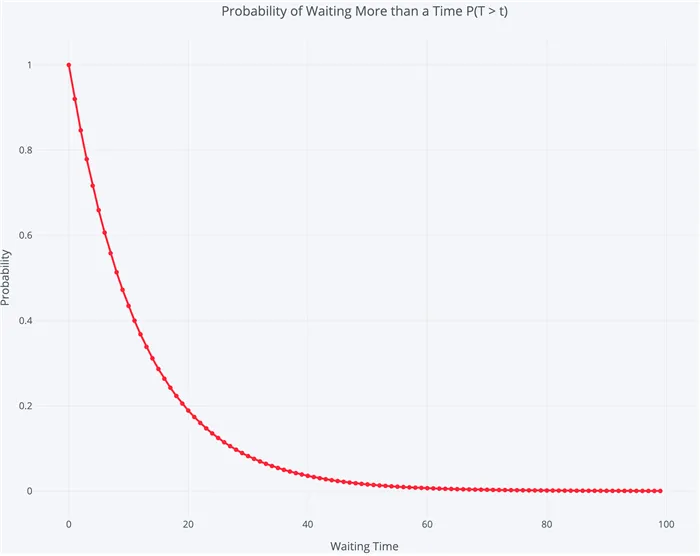
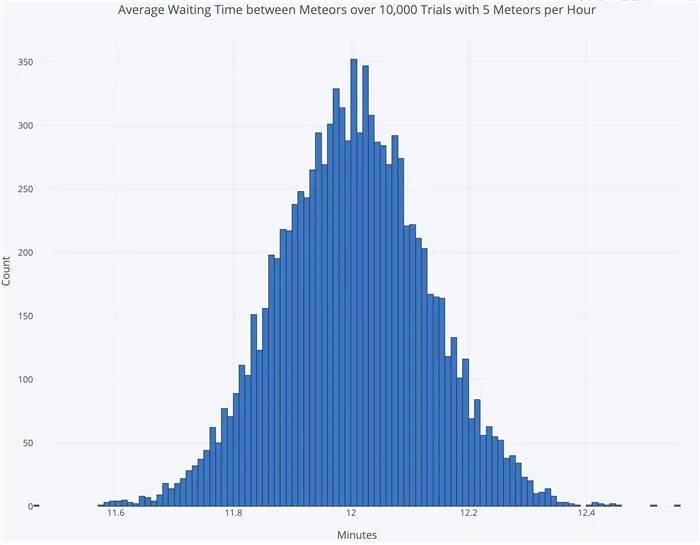
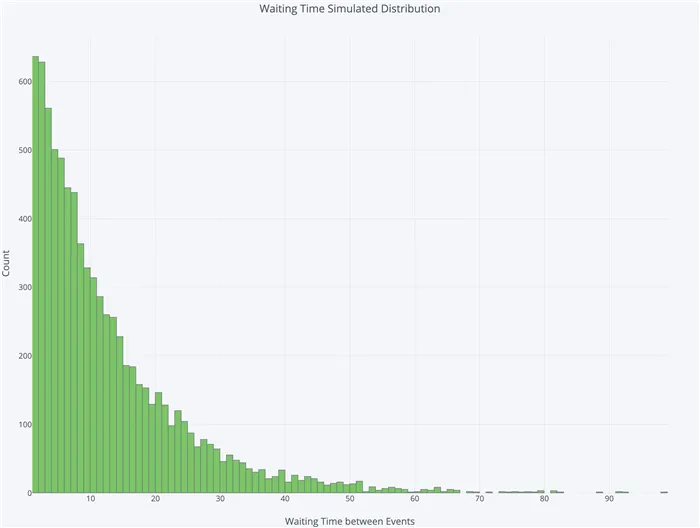
Чтобы ответить на вопрос о среднем времени ожидания, мы проводим 10 000 отдельных тестов, каждый из которых наблюдает за небом в течение 100 000 минут. На графике ниже показано распределение среднего времени ожидания между метеорами в этих испытаниях:
Распределение Пуассона и объяснение Пуассоновского процесса
Самое трагичное в статистике в большинстве школ — это то, насколько она скучна. Преподаватели часами анализируют выводы, уравнения и теоремы, а когда вы, наконец, доходите до самого интересного — применения концепций к реальным числам — они приводят вас к не относящимся к делу, лишенным воображения примерам вроде бросания игральных костей. Это очень жаль, потому что статистика может быть замечательной, если вы пропустите выводы (которые вам, вероятно, никогда не понадобятся) и сосредоточитесь на применении идей для решения интересных проблем.
В этой статье мы рассмотрим процессы Пуассона и распределение Пуассона, два важных понятия в теории вероятностей. Показывая только соответствующую теорию, мы проработаем реальный пример и представим уравнения и диаграммы, чтобы вписать идеи в контекст.
Пуассоновский процесс
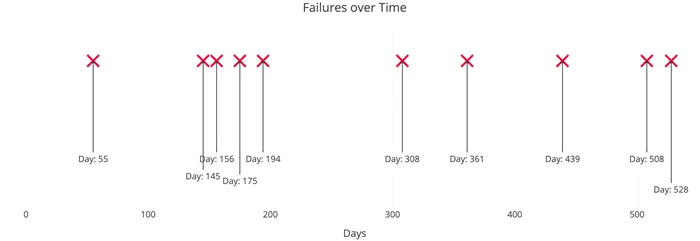
Процесс Пуассона — это модель для серии дискретных событий, где среднее время между событиями известно, но точное время наступления событий случайно. Наступление события не зависит от предыдущего события (время ожидания между событиями без памяти). Предположим, у нас есть сайт, с которого сеть доставки контента (CDN) сообщает нам, что ошибка происходит в среднем каждые 60 дней, причем одна ошибка не влияет на вероятность следующей ошибки. Все, что мы знаем, это среднее время между отказами. Это пуассоновский процесс, который выглядит следующим образом:

Важным моментом является то, что мы знаем среднее время между событиями, но они распределены случайным (стохастическим) образом. Возможны как одновременные сбои, так и сбои, длящиеся годами из-за случайности процесса.
Пуассоновский процесс отвечает следующим критериям (на самом деле, многие явления, моделируемые как пуассоновские процессы, не отвечают им в точности):
- События независимый друг друга. Возникновение одного события не влияет на вероятность другого события.
- Средняя скорость (события за период времени) постоянна.
- Два события не могут происходить одновременно.
Последний пункт — события не являются одновременными — означает, что мы можем рассматривать любой подинтервал пуассоновского процесса как процесс Бернулли, т.е. либо успех, либо неудача. На нашем сайте общий интервал может составлять 600 дней, но при каждом дополнительном интервале — один день — наш сайт либо отказывает, либо сохраняется.
Типичными примерами процессов Пуассона являются звонки клиентов в колл-центр, посетители веб-сайта, радиоактивный распад атомов, фотоны, попадающие в космический телескоп, и изменения цены акций. Процессы Пуассона обычно ассоциируются со временем, но это не так. Для запасов мы можем знать среднее движение в день (количество событий в год), но мы также можем иметь процесс Пуассона для количества деревьев на гектар (количество событий на площадь).
(Часто приводимый пример пуассоновского процесса — прибытие автобусов (или поездов, или теперь Ubers)). Однако это не настоящий пуассоновский процесс, поскольку поступления не зависят друг от друга. Даже в автобусных системах, которые не ходят по расписанию, задержка одного автобуса влияет на время прибытия следующего автобуса; Джейк ВандерПлюс написал отличную статью о применении процесса Пуассона к времени прибытия автобусов, который лучше работает с подготовленными данными, чем с реальными).
Распределение Пуассона
Процесс Пуассона — это модель, которую мы используем для описания случайных событий, но сама по себе она не очень полезна. Распределение Пуассона нужно нам для таких интересных вещей, как нахождение вероятности серии событий за определенный промежуток времени или вероятности ожидания следующего события.
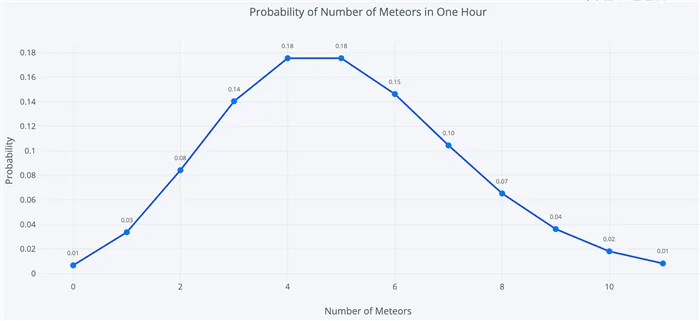
Функция массовой вероятности распределения Пуассона дает вероятность наблюдения K событий за период с учетом продолжительности периода и среднего значения событий за время:
Это несколько запутанно, и период времени/время* обычно упрощается до одного параметра, λ, лямбда, экспонента скорости. При такой замене функция вероятности распределения Пуассона теперь имеет один параметр:
Лямбду можно представить как ожидаемое количество событий в интервале. (Мы используем название этого интервала, потому что нам не обязательно использовать временной интервал, но и площадь или объем, основанный на процессе Пуассона). Мне нравится писать lambda, чтобы напомнить себе, что параметр скорости является функцией как среднего числа событий за время, так и длины периода, но в большинстве случаев вы обнаружите, что он чуть выше этого параметра.
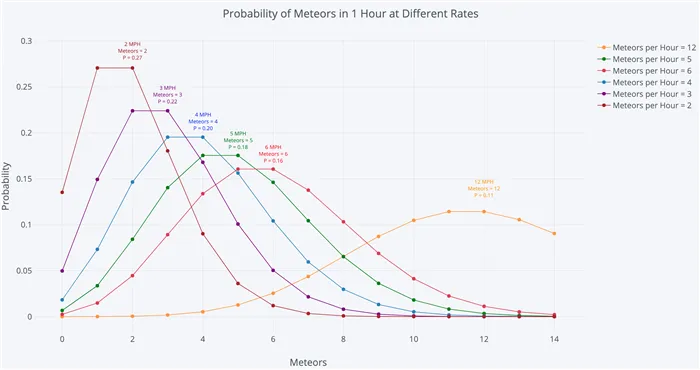
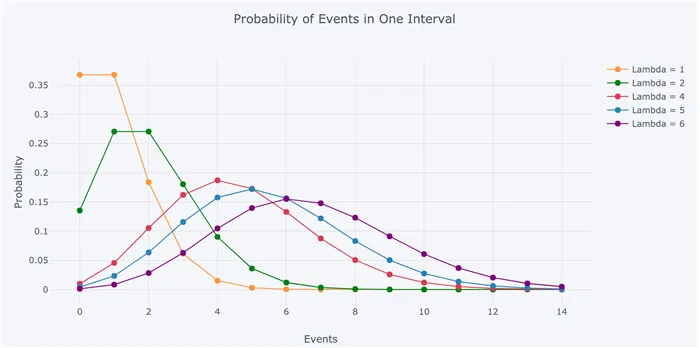
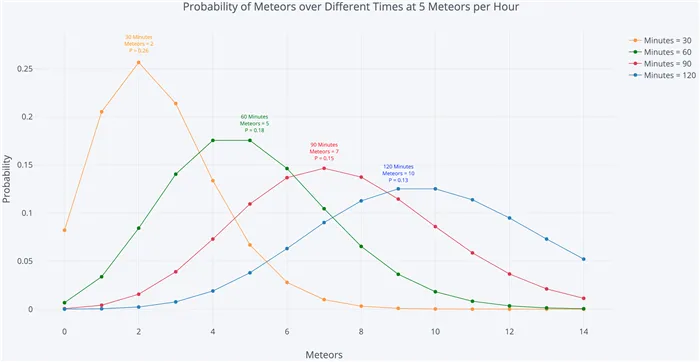
Если мы изменяем параметр скорости λ, мы изменяем вероятность увидеть различное количество событий в одном интервале Следующий график представляет собой функцию массовой вероятности распределения Пуассона, показывающую вероятность увидеть количество событий в интервале с различными параметрами скорости.
Наиболее вероятное число событий в интервале для каждой кривой — это параметр скорости, Это имеет смысл, потому что параметр скорости — это ожидаемое число событий в интервале, и поэтому, если это целое число, то параметр скорости — это число событий с наибольшей вероятностью,
Если это не целое число, то наибольшее число вероятностей событий — это целое число, наиболее близкое к параметру скорости, поскольку распределение Пуассона определено только для дискретного числа событий. Дискретная природа распределения Пуассона также объясняет, почему оно является функцией массы, а не функцией плотности. (Параметр скорости также является средним значением и дисперсией распределения, которые не обязательно должны быть целыми числами).
Функция массового распределения Пуассона может быть использована для определения вероятности наблюдения определенного количества событий в течение интервала, создаваемого процессом Пуассона. Другое применение уравнения массовой функции — как мы увидим позже — заключается в определении вероятности ожидания определенного интервала между событиями.
Теорема Пуассона.
Параметры биномиального распределения можно варьировать следующим образом
т.е. биномиальная вероятность стремится к вероятности Пуассона.
Доказательство.
Путем кластеризации множителей pk,nследующим образом
получаем
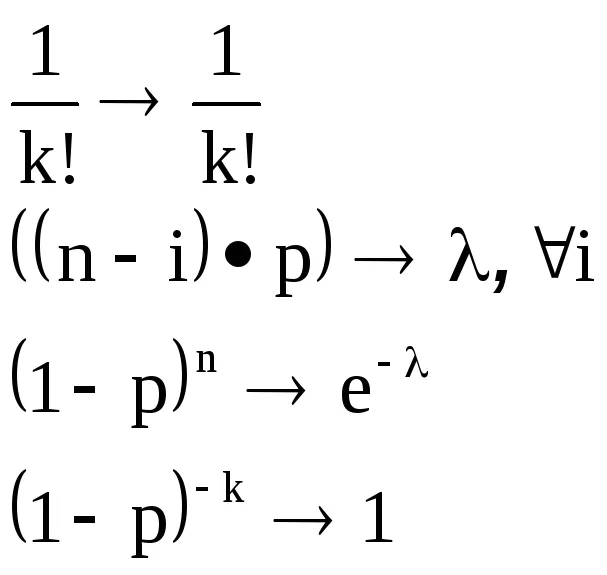
Для больших k гораздо проще вычислить вероятность Пуассона, чем биномиальную вероятность. Распределение Пуассона используется для аппроксимации биномиального распределения в случаях, когда число испытаний в системе Бернулли велико, а вероятность успеха мала.
Независимость событий и условная вероятность. Построение моделей.
При построении дискретных вероятностных моделей достаточно определить распределение на множестве элементарных исходов. Для определения вероятности элементарного исхода часто используют понятие независимости и понятие условной вероятности.
Этот пример показывает, что существуют попарно независимые события, которые не являются независимыми во множестве.
Рассмотрим тетраэдр, грани которого окрашены в три цвета следующим образом:
2-е лицо — зеленое.
Наконечник 3 — желтый
4-я сторона разделена на три зоны — синюю, зеленую и желтую.
Эксперимент заключается в бросании тетраэдра и наблюдении за цветом падающей поверхности (внизу).
A — край синий
B — лицо зеленого цвета
C — лицо желтое
Используя симметрию тетраэдра и классическую модель вероятности, получаем:
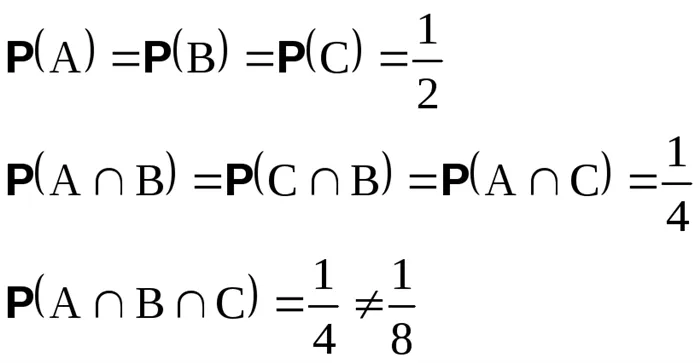
Чтобы избежать двусмысленности в интерпретации независимости в теории вероятностей, независимость в множествах в основном используется при построении таких моделей, как сильнейшая. Когда мы говорим о независимости в дальнейшем, мы имеем в виду независимость в целом, если не указано иное.
Использование понятия независимости для построения моделей. Произведение вероятностных пространств.
Во многих практических задачах априори ясно, что определенные случайные события в эксперименте являются независимыми. Очевидно, что эти события должны быть независимыми и в математической модели, описывающей рассматриваемый эксперимент. Определение независимости в теории вероятностей носит аналитический характер, и поэтому требование, чтобы события в модели были независимыми, приводит к ограничениям на используемые вероятности. Эти ограничения в сочетании с дополнительными качественными (симметрия) или количественными требованиями часто позволяют четко определить соответствующую вероятность.
Например, рассмотрим эксперимент, определяемый элементарным результатом вида

где первая координата описывает один случайный компонент, а вторая координата — другой случайный компонент опыта.
Предполагая, что N1изменения для первого компонента и N2— для второй компоненты, то для определения вероятности в общем случае нам потребуется N1*N2-1 вероятности элементарных исходов (столько-то пар минус одна — мы знаем, что сумма всех вероятностей пар должна быть равна 1).
Если мы заранее знаем, что компоненты независимы, то количество вероятностей событий, необходимых для однозначного определения вероятности, сводится к N1+N2-2 (N1-1 для первого компонента и N2-1 для второго компонента). Кроме того, вероятность элементарного исхода определяется как произведение вероятностей составляющих его значений.
Мы использовали аналогичную технику при построении моделей для системы Бернулли и полиномиальной системы.
В общем случае мы представляем элементарный результат эксперимента в виде вектора с n координатами.
Известно, что координаты вектора описывают независимые компоненты, т.е. все события из
должны быть независимыми. Если затем, для описания i-го компонента, мы используем вероятностное пространство
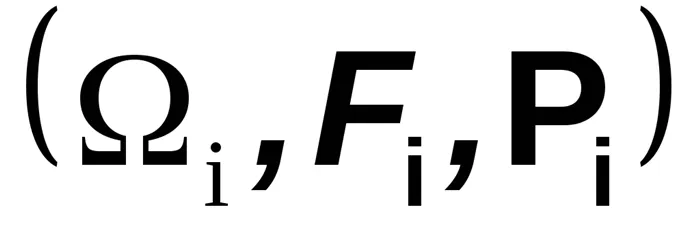
с соответствующими распределениями
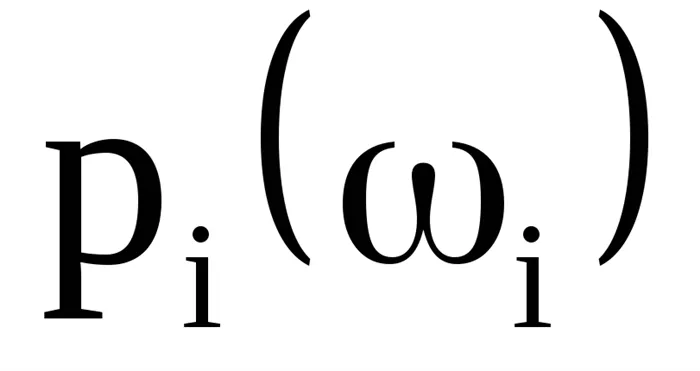
то очевидно, что для описания всего эксперимента можно использовать следующее вероятностное пространство
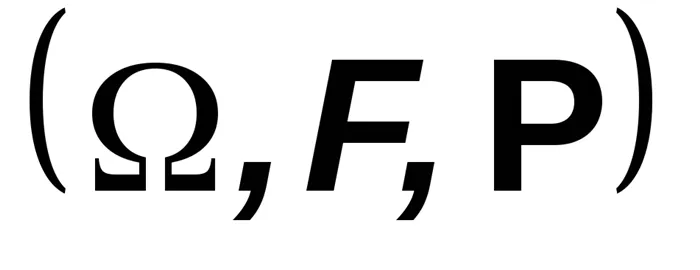
т.е. сигма-алгебру, содержащую все события, описывающие поведение компонентов.
Распределение в полученном пространстве определяется по следующей формуле.
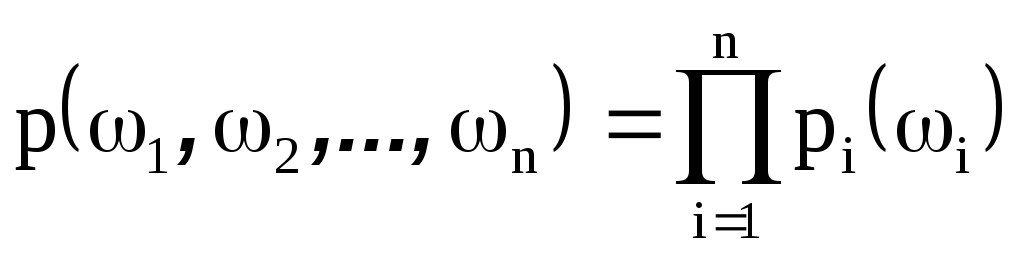
Таким образом, построенное вероятностное пространство является произведением вероятностных пространств

и его компоненты являются соответственно произведением пространств элементарных исходов, произведением сигма-алгебр и произведением вероятностных мер.
Пример править
Распределение Пуассона может быть полезно для моделирования событий, например.
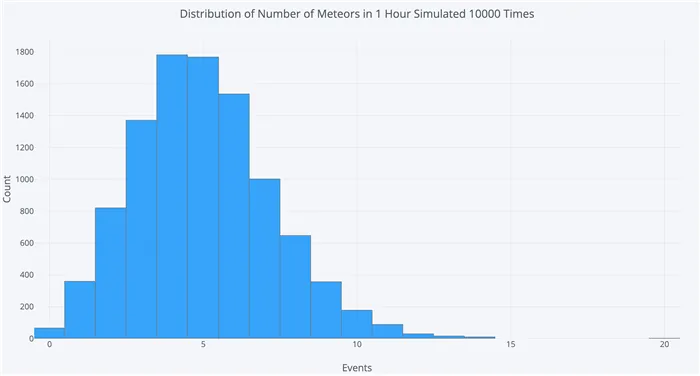
- Количество метеоритов диаметром более 1 метра, падающих на Землю за год.
- Количество пациентов, поступивших в отделение неотложной помощи с 22 до 23 часов.
- Количество лазерных фотонов, попавших в детектор за определенный промежуток времени.
Предположения и обоснованность править
Распределение Пуассона является подходящей моделью, если выполняются следующие предположения 4.
- k — количество раз, когда событие происходит в интервале, и k может принимать значения 0, 1, 2, .
- Возникновение одного события не влияет на вероятность того, что произойдет второе событие. То есть события происходят независимо.
- Средняя скорость, с которой происходят события, не зависит от каких-либо событий. Для простоты это обычно считается постоянным, но на практике может меняться со временем.
- Два события не могут происходить в один и тот же момент; вместо этого на каждом очень маленьком подынтервале происходит ровно одно событие, либо не происходит.
Если эти условия выполняются, то k является пуассоновской случайной величиной, а распределение k — распределением Пуассона.
Распределение Пуассона также является пределом биномиального распределения, где вероятность успеха для каждого испытания равна λ, деленная на число испытаний, а число испытаний стремится к бесконечности (см. раздел «Связанные распределения»).
Примеры вероятностей для распределений Пуассона править
На данной реке наводнение происходит в среднем один раз в 100 лет. Рассчитайте вероятность k = 0, 1, 2, 3, 4, 5 или 6 наводнений в течение 100-летнего интервала, предполагая, что подходит модель Пуассона.
Поскольку средняя частота событий составляет одно наводнение в 100 лет, λ = 1.
Вероятность от 0 до 6 наводнений за 100 лет.
Угарте и его коллеги сообщают, что среднее количество голов в футбольных матчах чемпионата мира составляет около 2,5, и модель Пуассона подходит. 5 Поскольку средняя частота событий составляет 2,5 гола за матч, λ = 2,5.
Вероятность того, что в матче будет забито от 0 до 7 голов.
Один раз в интервале событий: частный случай λ = 1 и k = 0 править
Предположим, по оценкам астрономов, крупные метеориты (выше определенного размера) падают на Землю в среднем раз в 100 лет (λ = 1 событие за 100 лет), и число падений метеоритов соответствует распределению Пуассона. Какова вероятность того, что метеорит k = 0 упадет в ближайшие 100 лет?
При этих предположениях вероятность того, что ни один крупный метеорит не упадет на Землю в ближайшие 100 лет, составляет примерно 0,37. Оставшиеся 1 — 0,37 = 0,63 — это вероятность того, что в ближайшие 100 лет упадет 1, 2, 3 или более крупных метеоритов. В приведенном выше примере наводнение в результате разлива происходит каждые 100 лет (λ = 1). Согласно тому же расчету, вероятность того, что через 100 лет наводнения не будет, составила 0,37.
Если событие происходит в среднем один раз за интервал (λ = 1) и события следуют распределению Пуассона, то P (0 событий в следующем интервале) = 0,37. Более того, P (ровно одно событие в следующем интервале) = 0,37, как показано в таблице для наводнений, связанных с наводнениями.
Примеры, нарушающие предположения Пуассона править
Маловероятно, что количество студентов, прибывающих в общежитие в минуту, соответствует распределению Пуассона, поскольку скорость не является постоянной (низкая скорость во время занятий, высокая скорость между занятиями), а отдельные студенты, прибывающие в общежитие, не являются независимыми (студенты обычно прибывают группами).
Число землетрясений магнитудой 5 в год в стране может не соответствовать распределению Пуассона, если сильное землетрясение увеличивает вероятность последующих толчков такой же силы.
Примеры, в которых гарантировано хотя бы одно событие, не распространяются, но могут быть смоделированы распределением Пуассона с числом отсечения, равным нулю.
Графовые распределения, в которых число интервалов с нулевыми событиями больше, чем предсказывается моделью Пуассона, могут быть смоделированы с помощью модели с нулевой дисперсией.








