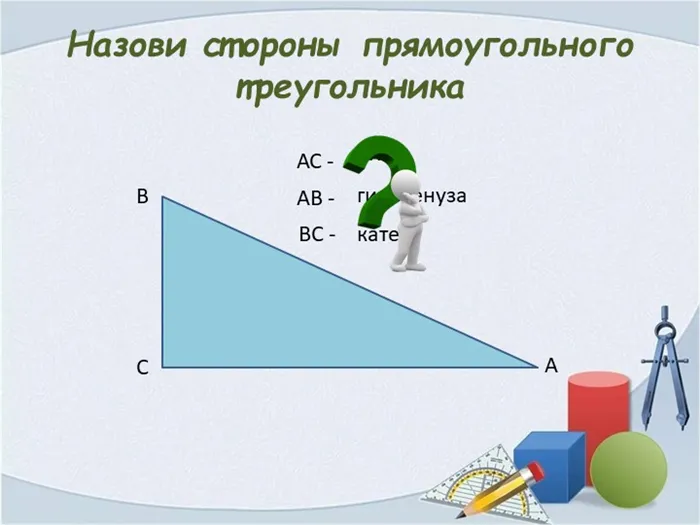
Сторона, противоположная прямому углу, называется гипотенузой (сторона c (рис. 1)). Другие стороны, т.е. стороны, примыкающие к прямому углу (стороны a и b ), называются перпендикулярными сторонами.
Признаки равенства прямоугольных треугольников
Для прямоугольных треугольников можно сформулировать следующие равенства:
1 балл (из двух пробников). Если два пробора одного правильного треугольника равны двум проборам другого правильного треугольника, то эти правильные треугольники равны (рис. 1).
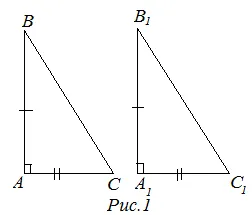
Второй признак равенства (по катету и гипотенузе)
2-й знак (от пробника и гипотенузы). Если перпендикуляр и гипотенуза одного правильного треугольника равны перпендикуляру и гипотенузе другого правильного треугольника, то эти треугольники равны (рис. 2).
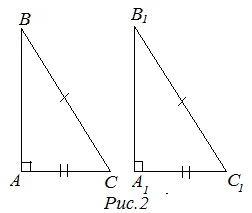
Третий признак равенства (по гипотенузе и острому углу)
Доказательство 3 (с гипотенузой и острым углом). Если гипотенуза и острый угол одного правильного треугольника равны гипотенузе и острому углу другого правильного треугольника, то эти треугольники равны (рис. 3).
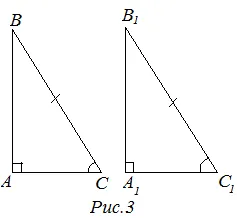
Первый признак равенства прямоугольных треугольников
Условия равенства правильных треугольников вытекают из трех условий равенства треугольников, но прямой угол деформирует их, а не расширяет, и делает их более простыми. Каждый из символов равенства правильных треугольников можно заменить одним из трех основных треугольников, но это заняло бы слишком много времени, поэтому были указаны 5 свойств и символов равенства правильных треугольников.
Очень часто вместо основного свойства равенства треугольников используется метод суперпозиции, когда две фигуры мысленно накладываются друг на друга. Это не означает, что это правильно или неправильно. Это просто еще один способ доказательства, который стоит рассмотреть. Однако не стоит думать, что каждый признак можно доказать простым наложением. Итак, давайте рассмотрим, как доказать равенство правильных треугольников с помощью трех основных доказательств равенства треугольников.
Первый пункт равенства правильных треугольников гласит: Два правильных треугольника равны, если два щупа одного треугольника равны двум щупам другого треугольника. Короче говоря, это равенство двух зондов.
Доказать этот принцип очень легко. При условии, что: две вершины правильного треугольника равны. Между зондами имеется прямой угол в 90 градусов, поэтому углы треугольников равны. Поэтому два треугольника равны по двум сторонам и углу между ними.
Второй признак
Второе доказательство состоит в следующем: Два правильных треугольника равны, если вершина и прилежащий острый угол одного треугольника равны вершине и прилежащему острому углу другого треугольника.
Второй признак доказывается тем же утверждением о равенстве прямых углов друг другу. Если треугольники по определению являются равными треугольниками с равными перпендикулярами, равными острыми углами и равными прямыми углами, то эти треугольники равны по второму равенству (сторона и два смежных угла).
Третий признак
Два правильных треугольника равны, если вершина и противолежащий острый угол одного треугольника равны вершине и противолежащему острому углу другого треугольника.
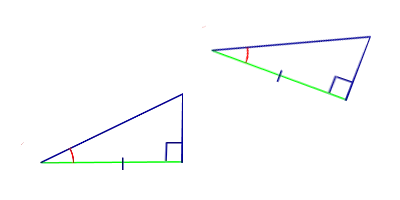
Сумма острых углов треугольника равна 90 градусам. Для простоты обозначим углы маленькими латинскими буквами. Один угол — прямой, два других обозначены как a и b в первом треугольнике и c и d во втором треугольнике.
Углы a и d равны согласно задаче.
Вычитаем угол a
Это означает, что если два прямых угла из двух прямых углов равны, то два других прямых угла также равны, поэтому мы можем использовать второе свойство.
Во втором и третьем пункте мы должны обратить особое внимание на острый угол, потому что прямые углы всегда равны.
Признаки равенства прямоугольных треугольников
Этот урок посвящен точкам равенства правильных треугольников с двумя перпендикулярами, с перпендикуляром и прилежащим острым углом, с гипотенузой и острым углом, с гипотенузой и перпендикуляром. Мы доказываем эти положения и используем их для решения проблем.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этим и другим видеоурокам из комплекта, вам необходимо добавить его в свой личный кабинет.


2. Распространите видеоуроки в своих личных кабинетах среди учеников.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Признаки равенства прямоугольных треугольников»
Первое доказательство равенства треугольников:
Если две стороны и угол между ними треугольника совпадают с двумя сторонами и углом между ними другого треугольника, то эти треугольники равны.

Вторая точка равенства треугольников:
Если одна сторона и два смежных угла треугольника равны одной стороне и двум смежным углам другого треугольника, то эти треугольники равны.
Используем точки равенства первого и второго треугольников и докажем следующие равенства правильных треугольников.
Теорема(о равенстве правильных треугольников из двух пробников):
Если вершины одного правильного треугольника равны вершинам другого правильного треугольника, то эти треугольники равны.

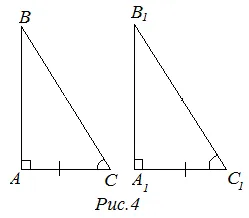
Возьмем два прямоугольных треугольника ABC и A1В1С1. Пусть зонд AC = A1С1и зонд BC=B .1С1. В прямоугольном треугольнике угол между пробами прямой, а два прямых угла равны. То есть, ∠C1=90 градусов. Мы предполагаем, что треугольники ABC и A.1В1С1равны в соответствии с первым принципом равенства треугольников. Теорема доказана.
Теорема(о равенстве правильных треугольников с пробором и прилежащим острым углом):
Если вершина и прилежащий острый угол прямоугольного треугольника равны вершине и прилежащему острому углу другого прямоугольного треугольника, то эти треугольники равны.

Пусть ABC и A — это1В1С1— являются правильными треугольниками, а пробник AC=A1С1и ∠A=∠A .1. Также ∠C=∠C1=90 градусов. Отсюда следует, что треугольники ABC и A1В1С1равны второму символу равенства треугольников. Теорема доказана.
Теорема(О равенстве правильных треугольников по гипотенузе и острому углу):
Если гипотенуза и острый угол прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то эти треугольники равны.
Пусть ABC и A — это1В1С1— правильные треугольники с ∠C=∠C1=90 градусов. Гипотенуза АВ и А1В1равны. Углы AB и A1также равны. В прямоугольном треугольнике сумма острых углов равна 90 градусам, т.е:
Отсюда следует, что гипотенуза AB и два смежных угла треугольника ABC равны гипотенузе A1В1и два смежных угла треугольника A1В1С1. Поэтому, согласно второму символу равенства треугольников, треугольники равны. Теорема доказана.
Задачи и решения
Задача 1: Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего из двух перпендикуляров равна 26,4 см. Найдите гипотенузу треугольника.
Решение. Обозначим через b меньший наклон, а через c — гипотенузу. Как сказано в условии задачи: c+b = 26,4 см.
Поскольку один из острых углов прямоугольного треугольника равен 60°, другой острый угол равен 90°-60° = 30°. Как известно, если угол равен 60°, то наибольшая сторона (пробник), а если угол равен 30°, то наименьшая сторона. Из свойства 2 следует, что меньшая сторона равна половине гипотенузы: или c =17,6 см.
Задача 2: Треугольники ABC и A1B1C1углы A и A1верны, BD и B1D1-являются биссектрисами углов. Докажите, что и BD = B1D1.
Доказательство. Поскольку BD и B1D1— являются биссектрисами углов и и (Теорема 1).
Отсюда следует, что треугольники BDC и B1D1C1равны (вторая точка равенства треугольников: (так как ).








