Презентация к уроку математики в 8 классе Функция корень из х презентация к уроку по алгебре (8 класс) на тему. Функция корень из х.

Содержание

Мы также включим свойство выпуклости в процесс чтения графов. Давайте «обозначим» этот процесс (продолжая нумерацию свойств, описанную ранее):

Давайте построим график этой функции. Исходя из определения корня квадратного, мы можем вычислять его только из неотрицательных чисел, то есть $x≥0$. Составим таблицу: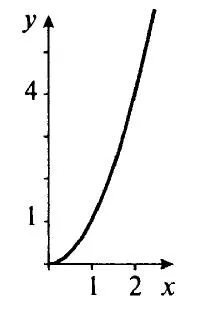Отметим наши точки на координатной плоскости.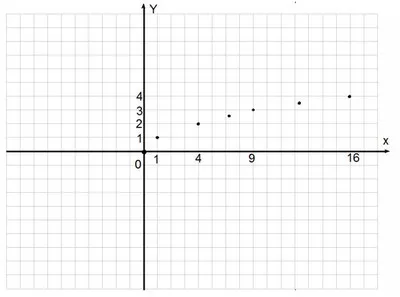Нам осталось аккуратно соединить полученные точки.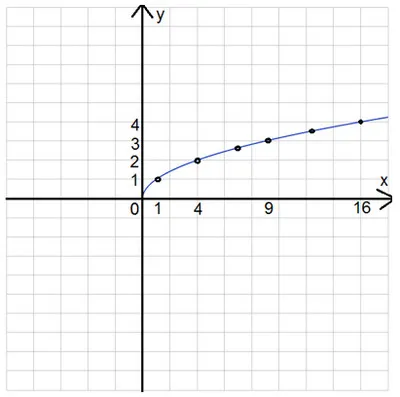Ребята, обратите внимание: если график нашей функции повернуть на бок, то получится левая ветка параболы. На самом деле, если строчки в таблице значений поменять местами (верхнюю строчку с нижней), то у нас получаться значения, как раз для параболы.

Используя график функции, свойства описать довольно таки просто. 1. Область определения:

Примеры решения функции квадратного корня

Пример 1: Найдите наибольшее и наименьшее значения квадратного корня функции в интервале: a) $4;9$. b) 3500;11$.

Решение. Мы можем решить наш пример двумя способами. В каждом письме описаны различные возможности.

α) Вернитесь к графику функции, построенному выше, и отметьте нужные точки отрезка. Мы ясно видим, что при $x=9$ функция больше всех остальных значений. Это означает, что в этот момент она достигает своего наибольшего значения. В точке $x=4$ значение функции меньше, чем во всех остальных точках, т.е. здесь она достигает своего наименьшего значения.

б) Мы знаем, что наша функция возрастает. Это означает, что каждому большему значению члена соответствует большее значение функции. Наибольшее и наименьшее значения достигаются на концах отрезка:

Пример 2. Решите уравнение:

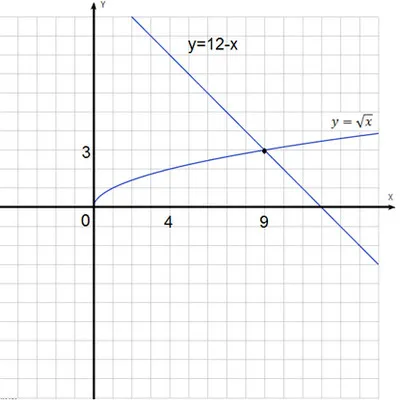
Решение. Самый простой способ — построить два графика функции и найти точку их пересечения. Точка пересечения с координатами $(9;3)$ хорошо видна на диаграмме. Следовательно, $x=9$ является решением нашего уравнения. Ответ: $x=9$.

Ребята, можем ли мы быть уверены, что других решений для этого примера не существует? Одна из функций возрастает, другая убывает. Как правило, они либо не имеют общих точек, либо пересекаются только в одной точке.

Постройте и прочитайте график функции:

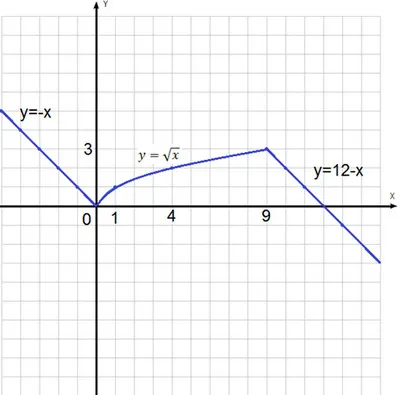
Нам нужно построить три частных графика функции, каждый на своем промежутке. Опишем свойства нашей функции: 1. Область определения: $(-∞;+∞)$. 2. $y=0$ при $х=0$ и $х=12$; $у>0$ при $xϵ(-∞;12)$; $y 4. \end $ 4. Постройте и прочитайте график функции: $y=\sqrt$.

Медиакомпания «mathematics-tests.com» зарегистрирована в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор). Свидетельство о регистрации СМИ EL № FS 77 — 63677 от 10 ноября 2015 г. Название — https://mathematics-tests.com.

Учредитель (соучредитель) издания сети СМИ mathematics-tests.com: Андреев Г.И., главный редактор СМИ: Андреев Г.И., телефон редакции: +7 (906) 384-18-43, e-mail: email protected mathematics-tests.com.

;+∞)$. 2. $у=0$ при $х=0$, $у>0$ при $х>0$. 3. Чем больше x, тем больше y. Таким образом, наша функция возрастает, т.е. мы движемся как бы «вверх». Функция растет на всем диапазоне определения. 4. на графике хорошо видно, что наименьшее значение функции равно 0 при $x=0$. Максимального значения не существует, функция непрерывно возрастает. 5. функция непрерывна. Мы не видим точек разрыва, везде проходит сплошная линия.

Допускается выделение другого свойства. Выпуклость. Принято считать, что функции являются выпуклыми либо вверх, либо вниз. Если мы посмотрим на нашу диаграмму, то увидим, что функция, похоже, изгибается вверх. 6. он изогнут вверх.

Значения, которые может принимать y, называются «множеством значений функции». Их также легко найти на графике. Посмотрите на область функции вдоль оси массива. Как изменяется функция: в сторону увеличения или уменьшения? 7. диапазон значений составляет ;+∞)$.

Презентация к уроку математики в 8 классе «Функция корень из х» презентация к уроку по алгебре (8 класс) на тему

Построение графика функции y= Цель урока: Научиться строить график функции и исследовать свойства функции. Научиться применять свойства функции при решении различных задач.

Решите уравнение: Вычисление:

Решите задачу: Постройте зависимость между длиной стороны квадрата и его площадью. Выясните, какие значения могут принимать переменные? Выясните, как меняется длина стороны квадрата в зависимости от его площади. S — независимая переменная a — зависимая переменная Выясните, является ли эта зависимость функцией. Для каждого значения независимой переменной существует свое значение зависимой переменной.

Построим график заданной функции S a O.o. 0 1 4 9 16 0 0 1 1 2 3 4 S a 0 1 1 Свойства функции: 1. S.o. 2. график проходит через t. (0;0) 3. график лежит в квадратичной I-образной прямой 4. функция возрастает

№ 352, 354 № 355 Если y = 1,2, то x ≈ 1,4.

Источник шаблона. Спасибо за внимание!

По теме: методические разработки, презентации и конспекты

Презентация на уроке математики «Повторение. Веселая математика. «Веселая математика».

Цель урока — усилить познавательный интерес к изучению математики и развить познавательные способности учащихся.

Подробный конспект и презентация на уроках математики по теме «Площадь треугольника» к учебнику С.А. Козловой Математика, 5 класс.

Данная разработка содержит конспект и презентацию для уроков математики по теме «Площадь треугольника» и тест по учебному материалу.

Презентация интегрированного урока математики для 7 класса по теме «Здоровье и экология в преподавании математики».

Презентация на уроке с естественной минуткой, упражнением для глаз, разделена на четыре файла: 1-5 слайды, 6-10 слайды, 11-34 слайды, 35-36 слайды.

Конспект урока математики в 9 классе по теме «Системы рациональных неравенств». Презентация урока математики в 9 классе по теме «Системы рациональных неравенств».

Материал данного урока направлен на рассмотрение решения линейных неравенств; формирование понятия «системы рациональных неравенств», «решение рациональных неравенств»; формы.

Презентация на уроках математики в 8 классе «Квадратные корни. Арифметический квадратный корень».

Презентация к уроку «Квадратные корни. Арифметический квадратный корень» (урок первый и второй).

Презентация к уроку в 5 классе «Корень слова».

Данная презентация является иллюстративным материалом к уроку русского языка в 5 классе. Тема и номер урока в теме: Формула. Орфография. Тема: Корень слова.

Функция корень из х

Поурочное планирование по алгебре для 8 класса. Направлен на работу с учебным пособием Макарычева. 8 класс алгебра. Просветление. Глава 2. ЧЕТЫРНАДЦАТЬ РОРОНОВ (19 уроков). §5 Арифметический квадратный корень (5 часов). Уроки 29, 30. Функция y = √x и ее график. Вернуться к списку тематических курсов по дизайну .

Уроки 29, 30. Функция у = √x и ее график

Цель: изучить функцию y = √x, ее свойства и график. Ожидаемые результаты: Знание основных свойств и графика функции y = √x. Тип курса: практические занятия.

Предположим, что длина стороны квадрата равна a (см), а его площадь — S (см2 ). Величины S и a связаны соотношением S = a 2 (при a ≠ 0). Это равенство означает, что для каждого значения стороны a квадрата существует только одно значение площади S. Из равенства S = a 2 следует a = √S. Это уравнение означает, что для каждого значения площади S квадрата можно определить единственное значение стороны a. Формулы S = a 2 (при a ≥ 0) и a = √S определяют функциональные зависимости между одними и теми же переменными a и S. Однако в первом случае независимой переменной (аргументом) является сторона квадрата a, а зависимой переменной (значением функции) — площадь S. Во втором случае, однако, независимой переменной (аргументом) является площадь квадрата S, а зависимой переменной (значением функции) — сторона a. Заметим, что функции S = a 2 (при a ≥ 0) и a = √S взаимно обратны.

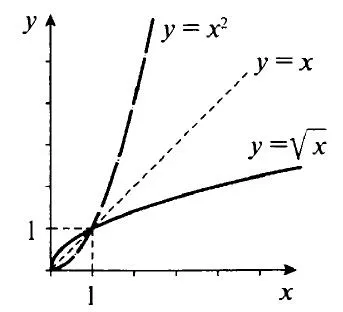
В предыдущем примере, если мы, как обычно, обозначим независимую переменную через l:, а зависимую переменную через y, то получим взаимно обратные функции y = x 2 (при x ≥ 0) и y = √x. Давайте сравним свойства и графики этих функций.

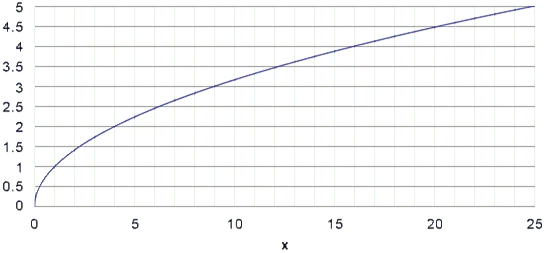
Сначала создайте таблицу со значениями функции y = √x и нарисуйте ее график.

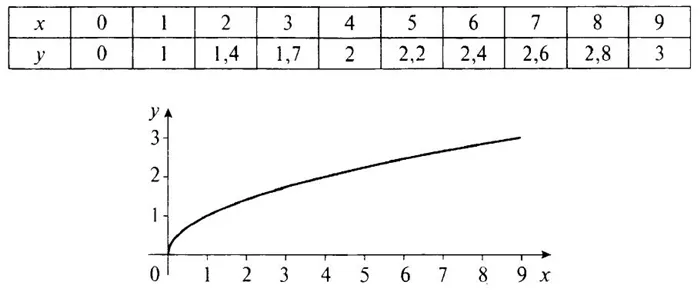
Назовите основные свойства функции y = √x .

Область определения функции — значения х ≥ 0.
Область изменения (значений) функции — значения у ≥ 0.
График функции пересекает оси координат в начале системы координат.
Значения функции у ≥ 0 при х ≥ 0, и график расположен в первой координатной четверти.
Функция монотонно возрастает.

Определим монотонную функцию. Пусть числа x₁и х₂принадлежат области определения функции, а значения функции в этих точках y₁и y₂соответственно. Пусть (для определенности) x₂>х₁. Если для всех этих значений x₁и х₂:

у₂>у₁(т. е. большему значению аргумента соответствует большее значение функции), то функция возрастает (график идет вверх);
у₂<у₁(т. е. большему значению аргумента соответствует меньшее значение функции), то функция убывает (график идет вниз).

Функция y = x 2, ее свойства и график изучались в седьмом классе. Отзывосновные свойстваэтой функции для x ≥ 0.

Область определения функции — значения х ≥ 0.
Область изменения (значений) функции — значения у ≥ 0.
График функции пересекает оси координат в начале системы координат.
Значения функции у ≥ 0 при х ≥ 0, и график расположен в первой координатной четверти.
Функция монотонно возрастает.

Творческие задания

Домашнее задание: № 352 (b); 356; 358 (c, d); 361; 362 (b); 363 (b, e, f); 365 (b, d).

Поурочное планирование по алгебре для 8 класса. Единая методология Макарычева (Просвещение), глава 2. Четвертый класс (19 часов). §5 Арифметический квадратный корень (5 часов). Уроки 29, 30. Функция y = √x и ее график.

Нахождение выражения из Х

В общем случае формула производной корня из x равна дроби с 1 в числителе и 1 в знаменателе, произведению степени корня на корень той же степени в частном корне выражения, в котором находится неизвестное, уменьшенному на 1. Математически это предложение можно выразить следующей формулой: ( n √x)’ Эта формула получается из следующей формулы: (n √ x = 1 / (n * n √ x n-1 ).

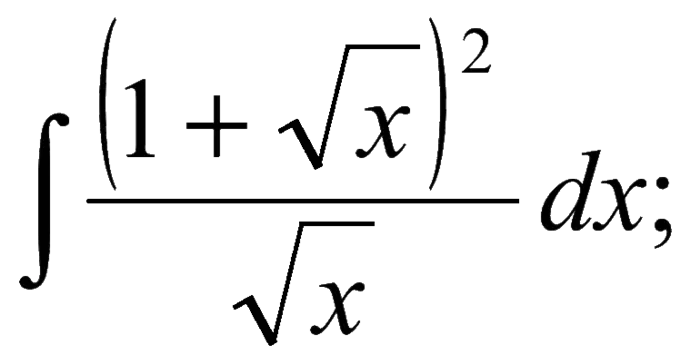
Эта формула называется первой формой. Он подходит для использования в выражениях произвольной кратности. Например, рассмотрим производную квадратного и кубического корня.

Таким образом, для квадратичного уравнения выражение будет таким: (n√x)’ = 1 / 2 * √x. То есть производная квадратного корня из x — это дробь, делитель которой равен единице, а делитель состоит из двух, умноженных на квадратный корень из неизвестного.

Аналогичную теорему можно сформулировать для производной кубического корня из x. В этом случае решением задачи на производную является дробь, числитель которой равен единице, а знаменатель — произведению трехкратного кубического корня из x и силы двух. Формула для расчета выглядит следующим образом: ( 3 √x)’ = 1 / (3 3 √x 2 ).

Вы заметите, что операция ограничена теми же операциями, которые выполняются для экспоненциализации дробей, когда делитель равен той же экспоненте.

Другими словами, вычисление производной родительского выражения сводится к использованию формул для нахождения функции дроби.

Для доказательства формул используются следующие рассуждения. Производная переменной по квадратному корню — это то же самое, что и нахождение функции по многочлену в степени единицы: (√x)’ = (x ½ )’. Поэтому мы можем использовать формулу для вычисления производной от неизвестного числа в степени en. Это означает, что обозначение (x ½ )’ = ½ x-½ = 1 / (2√x) является правильным.

Формула для производной третьей степени доказывается по тому же принципу. Применяя правило дифференцирования и переписывая кубический корень в виде трехкратной степени, мы можем записать: ( 3 √x )’ = (x 1/3 )’ = 1 / 3 * (x- 2/3 ) = 1 / 3 * ( 3 √x 2 ) Обратите внимание, что степен ь-2/3 образуется путем вычитания 1 из дроби с 2 в числителе и 3 в знаменателе.

Примеры заданий

При выводе функции f (x) = n √x m необходимо перевести корень в степенную форму: f (x)’ = ( n √x m )’ = x m/n .

Поскольку из производных по степени известно, что (x m )’ = m * x m-1, алгоритм решения для нахождения ответа на выражение корня сводится к преобразованию исходного уравнения путем перевода его в степень: f (x)’ = ( n √x m )’ = (x m/n )’ = m/n * x ( m/n) -1 = (m/n * n √x m-n ).

Это позволяет избежать запоминания сложной формулы, которая часто используется на практике.

Чтобы закрепить теорию, необходимо решить несколько типичных примеров:

Определить, чему будет равна производная от корня квадратного, кратного разности три минус икс в квадрате. Запись условия задачи выглядит так: (√ 3 — x 2 )’. Мысленно можно обозначить выражение в скобках буквой S. Получается, что задача будет состоять в поиске производной (√ S)’. Используя знание формулы, можно утверждать, что (√ S)’ = S’ / (2 * √ S). Ту же самую формулу можно будет получить, воспользовавшись преобразованием задания в степенную функцию: (√ S)’ = (S ½ ) ‘ = (½) * S (½ — 1 ) * S’ = S -½ * S’ / 2 = S’ / (2 * √ S). Таким образом, (√ 3 — x 2 )’ = (3 — x 2 )’ / (2 * √ 3 — x 2 ) = — 2* x / 2 * √ 3 — x 2 = — x / √ 3 — x 2 .
Рассчитать, чему будет равна производная функции 1 / (2 * 3√ x7). Исходное выражение нужно преобразовать так, чтобы неизвестная оказалась в числителе, а затем уже воспользоваться стандартным алгоритмом: (1 / 2 * 3√ x7)’ = 1 / 2 * (x-7/3)’. Теперь нужно взять производную от степенной функции. В итоге получится выражение: 1 / 2 * (-7 / 3) * x (-7/3) — 1 = -(7 / 6) * x-10/3 = (-7 / 6) * (1 / 3√ x10).
Необходимо найти производную суммы многочленов: p (x) = 3 + 4 √ x+3. По теореме дифференцирования ответ будет равняться сумме производных каждого члена равенства: p (x)’ = (3)’ + (4 √ x+3)’. Первое слагаемое равняется нулю, поэтому останется только найти производную корня. Используя снова правило производной, выражение можно переписать как 4 * (√ x+3)’. На следующем этапе многочлен в скобках нужно представить в виде степенной функции: (√x + 3)’ = 1 / ((2√x + 2)) * (x + 2)’ = 2 * (x +2)’ / √x+2. Так как производная суммы, это то же самое, что сумма производных, то будет верным записать: (4 √ x+2)’ = (2 / √x+2) *(). Производная для двойки равна нулю, поэтому плюсовать её смысла нет. В итоге получится: p (x)’ = (3 + 4 √ x+3)’ = 2/ √x +2 = 2 / √x +2.

Расчёт на онлайн-калькуляторе

После того как вы попрактикуетесь в решении различных примеров, найти производную от корня простого выражения будет довольно просто. Однако проблемы могут возникнуть, если задачи содержат двойные корни или если сама функция содержит большой многочлен. Эти проблемы обычно связаны не с алгоритмом решения, а со сложностью вычислений и преобразований.

Такие проблемы требуют большей внимательности и тщательности в расчетах. В этом случае поиск ответа может занять много времени. Поэтому в Интернете существуют онлайн-калькуляторы, которые помогают находить производные радикальных функций.

Это сервисы, которые предлагают бесплатные услуги по автоматическому вычислению производной любой сложности. Ими может пользоваться каждый, у кого есть доступ в Интернет. Для поиска ответа не требуется специальных знаний. Все, что вам нужно сделать, это ввести условие в предложенную форму и нажать кнопку «Рассчитать». Весь процесс расчета занимает одну-две секунды.

При этом большинство сервисов предлагают не только ответ на своих страницах, но и возможность просмотреть теоретический материал и предложить решение задач различной сложности. Поэтому не следует задавать вопрос о том, как получен тот или иной ответ.

Из различных веб-калькуляторов, рассчитывающих производные, можно выделить следующие:

Webmath.
Kontrolnaya-rabota
Onlinemschool.
Сalc.
Nauchniestati.

Веб-сайты, используемые для расчетов, отличаются интуитивно понятным пользовательским интерфейсом, не содержащим ненужной информации. На их страницах нет рекламного или вирусного кода.

Примечательно также, что после нескольких вычислений пользователь учится вычислять производную самостоятельно. И особенностью этих ресурсов является их способность к обучению. Помимо мгновенного ответа, программа-калькулятор предоставляет вам пошаговый расчет с комментариями.

Помимо студентов, калькуляторы будут полезны и инженерам. Даже небольшая ошибка в расчетах приведет к неправильному ответу. При этом исключается ошибка в автоматических расчетах.

Исследование функции y корень из x. «Функция «корень из х», её свойства и графики»

Квадратный корень является элементарной функцией и частным случаем функции мощности в. Арифметический квадратный корень гладкий в, а ноль непрерывен справа, но не дифференцируем.

Как функция, корень комплексной переменной — это двузначная функция, листья которой сходятся к нулю.

Преобразования графика функции квадратного корня.

Определите, какие преобразования функции необходимо выполнить, чтобы построить графики функций. Давайте определим типы преобразований.

Переместите функцию вверх по оси OY на 4 единицы.

Переместите функцию на 1 единицу вправо по оси OX.

График в три раза приближается к оси OY и уменьшается вдоль оси OX.

График смещается в сторону от оси OX OY.

График отходит от оси OY в 2 раза и расширяется вдоль оси OX.

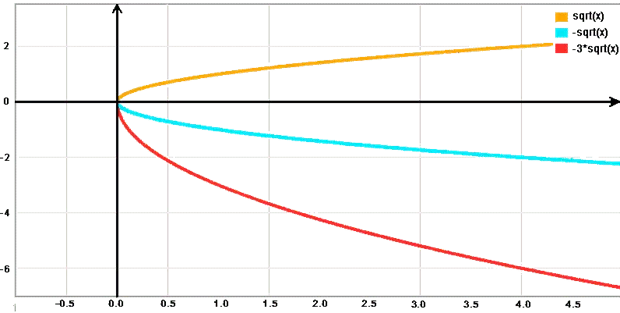
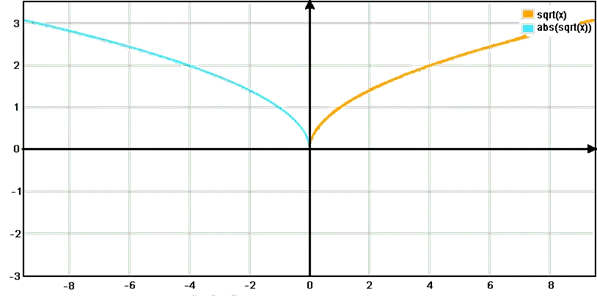
Часто преобразования функций комбинируются.

Например, необходимо построить график функции OY на одну единицу правее по оси OX и одновременно растянуть его в 3 раза по оси OY.

Иногда перед построением графика функции необходимо выполнить идентичные преобразования или упрощения функций.

N-й степени из действительного числа, отмечая, что корень любой степени (второй, третьей, четвертой и т.д.) можно извлечь из любого неотрицательного числа, а корень любой нечетной степени — из отрицательного числа. Но затем нам нужно подумать о функции такой формы, ее графике и свойствах. Мы сделаем это в следующем разделе. Сначала обсудим функцию для неотрицательных значений аргумента.

Начнем с известного вам случая, когда n =2, т.е. с функции На рис. 166 изображен график функции и график функции у = х 2, х>0. Оба графика представляют собой одну и ту же кривую, ветвь параболы, но они находятся в разных положениях в координатной плоскости. Чтобы пояснить, эти графики симметричны относительно прямой y = x, потому что состоят из точек, симметричных относительно этой прямой. См: На рассматриваемой ветви параболы y = x 2 расположены точки (0; 0), (1; 1), (2; 4), (3; 9), (4; 16), а на графике функции — точки (0; 0), (1; 1), (4; 2), (9; 3), (16; 4).

Точки (2; 4) и (4; 2), (3; 9) и (9; 3), (4; 16) и (16; 4) симметричны относительно прямой y = x (а точки (0; 0) и (1; 1) лежат на этой прямой). И вообще, для каждой точки (a; a 2) на графике функции y = x 2 существует точка (a 2 ; a), симметричная относительно прямой y = x на графике функции, и наоборот. Имеет место следующая теорема.

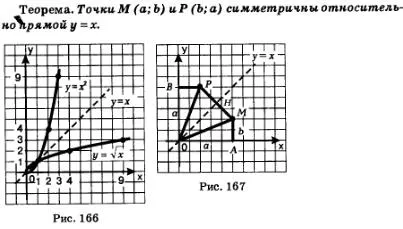
Доказательство. Будем считать для определенности, что а и b — положительные числа. Рассмотрим треугольники ОАМ и ОВР (рис. 167). Они равны, значит, ОР = ОМ и поскольку прямая у = х — биссектриса угла АОВ. Итак, треугольник РОМ — равнобедренный, ОН — его биссектриса, а значит, и ось симметрии. Точки М и Р симметричны относительно прямой ОН, что и требовалось доказать. Итак, график функции можно получить из графика функции у = х 2, х>0 с помощью преобразования симметрии относительно прямой у = х. Аналогично график функции можно получить из графика функции у = х 3, х>0 с преобразованием симметрии относительно прямой y = x; график функции может быть получен из графика функции с преобразованием симметрии относительно прямой y = x и т.д. Вспомните, что график функции напоминает ветвь параболы. Чем больше n, тем круче эта ветвь поднимается в пространстве и тем больше она приближается к оси x вблизи точки x = 0 (рис. 168).