— На этом рабочий день в нашем научно-исследовательском институте заканчивается. Мы помогли восстановить утраченную информацию о положительных и отрицательных числах.
Определение целых чисел
Целое число — это натуральное число и его противоположность — ноль. Примеры целых чисел: -7, 222, 0, 569321, -12345 и т.д.
Что нужно знать о целых числах:
- Сумма, разность и произведение целых чисел в результате дают целые числа.
- Не существует самого большого и самого маленького целого числа. Этот ряд бесконечен. Наибольшего и наименьшего целых чисел — не бывает.
- Обыкновенные и десятичные дроби нельзя назвать целыми числами. Но иногда в задачах можно встретить целые числа, у которых дробная часть равна нулю и при этом нет долей.
На оси чисел целые числа выглядят следующим образом:
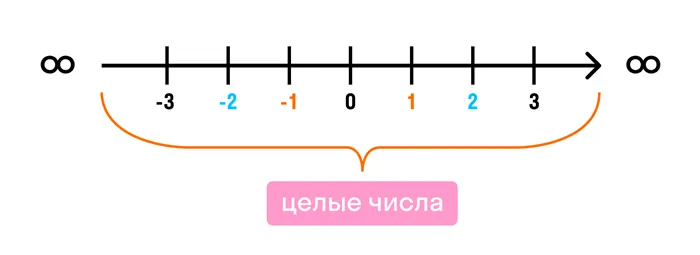
На координатной прямой точка отсчета всегда начинается с 0. Все отрицательные целые числа находятся слева, а все положительные целые числа — справа. Каждая точка соответствует целому числу.
Каждая точка на прямой, координата которой является целым числом, может быть достигнута через определенное количество единичных отрезков от начала координат.
Натуральные числа — это целые положительные числа, которые мы используем для измерения. К ним относятся.
Множество целых чисел — это расширенное множество натуральных чисел, которое может быть получено путем сложения нуля и отрицательных чисел, противоположных натуральным числам. Множество целых чисел обозначается Z.
Это выглядит примерно так:
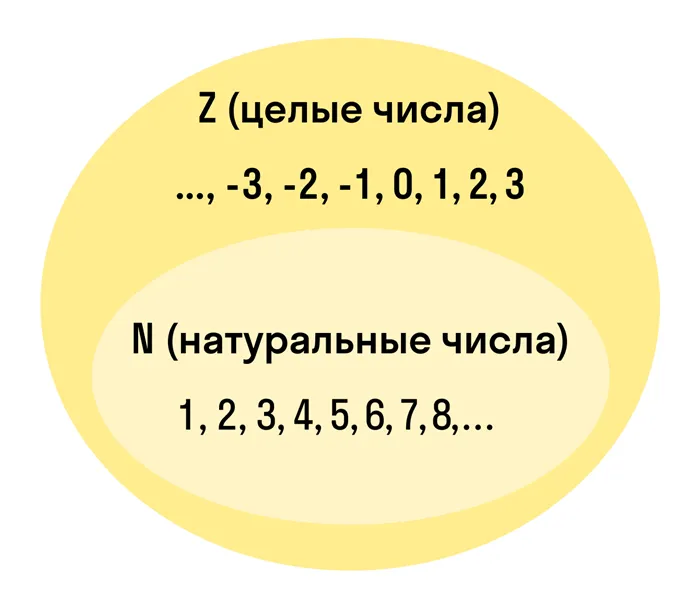
Последовательность целых чисел можно записать следующим образом:
∞ +. -4, -3, -2, -1, 0, 1, 2, 3, 4 … + ∞
Уроки математики помогут вам улучшить свои оценки и подготовиться к контрольным работам, зачетам и экзаменам.
Выясните, по каким предметам вы «отстаете», а затем — приведите их в порядок без заучивания формул и скучных лекций.

Свойства целых чисел
Таблица содержит основные свойства сложения и умножения для любых целых чисел a, b и c:
Недвижимость
добавить
Умножение
Сложение a + (b + c) = (a + b) + c
a * (b * c) = (a * b) * c
a ≠ ±1 ⇒ 1/α не является целым числом
a * (b + c) = (a * b) + (a * c)
Два слова о разделении. В стандартной форме число нельзя разделить на набор целых чисел, но можно разделить на остаток. Это правило можно сформулировать следующим образом:
- Для всяких целых a и b (b ≠ 0), есть один набор целых чисел q и r. При этом:
a = bq + r, где a — делитель, b — делимое, q — делитель и r — остаток,
Положительные и отрицательные целые числа
Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля находятся целые положительные числа. Слева от нуля живут целые отрицательные числа.
Отрицательные целые числа — это целые числа со знаком минус. Они всегда меньше нуля. Примерами отрицательных целых чисел являются: -944, -1287, -1, -19.
Целые положительные числа — это целые числа со знаком плюс. Они всегда больше нуля. Примерами целых положительных чисел являются: 13, 401, 55, 29, 29, 12345.
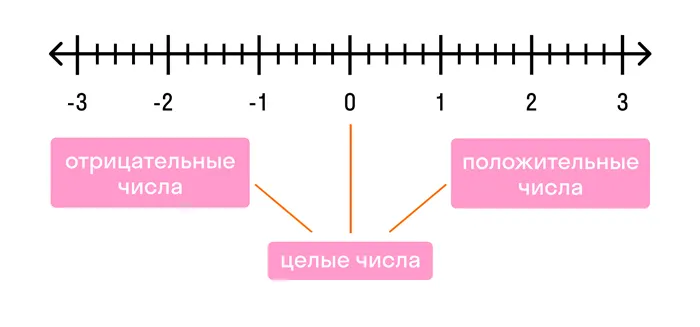
Бесконечное множество — это множество целых положительных и отрицательных чисел.
Если мы выберем любые два целых числа, то числа между ними можно назвать конечным множеством.
Например, запишите целые числа о т-4 до 3. Все числа между этими числами являются частью конечного множества. Заданное конечное множество чисел выглядит следующим образом:
Пример 1. Сколько целых чисел находится между числам и-30 и 100?
- Можно построить прямую и посчитать сколько отрезков находится между заданными числам.
- Или можно посчитать в уме: у нас есть 29 отрицательных числа, нуль и 99 положительных чисел.
Пример 2. Сколько нечетных целых чисел находится между числам и-4 и 5?
- Выпишем все целые числа, которые находятся между -4 и 5: -3, -2, -1, 0, 1, 2, 3, 4
- Подчеркнем нечетные числа в данному ряду.
Занимайтесь по 15 минут в день. Освоить английскую грамматику и лексику. Сделайте язык частью своей жизни.

Положительные и отрицательные числа
Чтобы понять, что означают положительные и отрицательные числа, давайте сначала проведем прямую линию и отметим точку 0 (ноль), которая считается началом.
Расположим ось в наиболее распространенном горизонтальном направлении. Стрелка показывает положительное направление линии (слева направо).
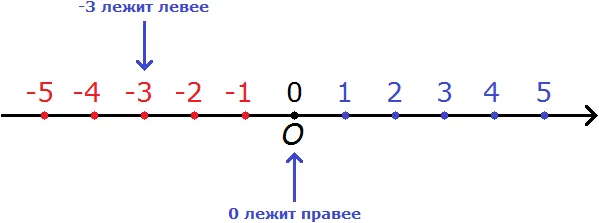
Сразу же отметим, что число «ноль» не относится ни к положительным, ни к отрицательным числам.
Положительные числа
Если мы начнем отсчитывать отрезки справа от нуля, то полученные отметки соответствуют положительным числам, равным расстоянию от 0 до этих отметок. Таким образом, мы получили числовую ось.
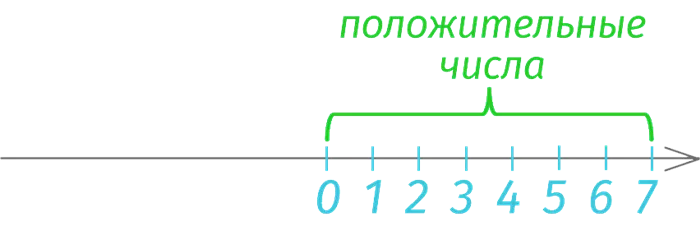
Полная нотация положительных чисел включает символ «+» спереди, т.е. +3, +7, +12, +21 и т.д. Однако «плюс» обычно опускается и только подразумевается:
- “+3” – это то же самое, что и просто “3”
- +7 = 7
- +12 = 12
- +21 = 21
Примечание: Любое положительное число больше нуля.
Отрицательные числа
Когда мы начинаем отсчитывать части слева от нуля, мы получаем отрицательные числа вместо положительных, потому что мы движемся в направлении, противоположном направлению прямой линии.

Отрицательные числа записываются, предваряя их знаком минус, который никогда не опускается: -2, -5, -8, -19 и т.д.
Примечание: Любое отрицательное число меньше нуля.
Отрицательные числа, как и положительные, необходимы для выражения различных математических, физических, экономических и других величин. Например:
- температура воздуха (-15°, +20°);
- убыток или прибыль (-240 тыс. руб., 370 тыс. руб.);
- абсолютное/относительное уменьшение или увеличение определенного показателя (-13%, + 27%) и т.д.
Публикации по теме:
- Факториал числа
- Показатель степени: определение и свойства
- Числа Фибоначчи
- Число Эйлера (e)
- Решение квадратных уравнений
- Определение логарифма, его свойства и график
- Степени натуральных чисел
- Формулы сокращенного умножения
- Свойства корней в степени n
- Арифметическая прогрессия: определение, формулы, свойства
- Производные логарифмов: формулы и примеры
- Производная функции: правила и формулы дифференцирования
- Нахождение производной степенной функции
- Десятичный логарифм числа
- Логарифм степени (коэффициент перед логарифмом)
- Логарифм корня (дробный коэффициент перед логарифмом)
- Логарифмическая функция
- Решение логарифмических неравенств
- Квадрат суммы: формула и примеры
- Куб разности: формула и примеры
- Сумма кубов: формула и примеры
- Разность кубов: формула и примеры
- Теорема Безу: нахождение остатка от деления многочлена на двучлен
- Обыкновенные (простые) дроби
- Правильные, неправильные и смешанные дроби
- Правила сравнения обыкновенных дробей
- Основное свойство дроби
- Сокращение обыкновенных дробей
- Сложение обыкновенных дробей
- Вычитание обыкновенных дробей
- Умножение обыкновенных дробей
- Понятие десятичной дроби
- Перевод десятичной дроби в обыкновенную
- Перевод обыкновенной дроби в десятичную
- Умножение десятичных дробей: правила, примеры
- Деление десятичных дробей: правила, примеры
- Сложение десятичных дробей: правила, примеры
- Вычитание десятичных дробей: правила, примеры
- Способы сравнения десятичных дробей
- Округление десятичных дробей: правила, примеры
- Модуль комплексного числа z: определение, свойства
- Решение уравнений с модулем
- Решение неравенств с модулем
- Что такое среднее арифметическое чисел: двух, трех, четырех и тд
- Алгебраическая сумма
- Правила раскрытия скобок с примерами
- Тождественные преобразования выражений
- Что такое линейная функция: определение, формула, график
- Что такое квадратный трехчлен: определение, формула, график, примеры
- Гипербола: определение, функция, формула, примеры построения
Отрицательные числа
Предположим, что на улице зима. Какую температуру будет показывать указатель температуры воздуха?
Зимой здесь холодно. Поэтому обычно говорят, что температура ниже нуля, т.е. манометр не поднимается выше 0.
В математике такие числа называются отрицательными, и когда они записываются, перед ними должен стоять знак минус.
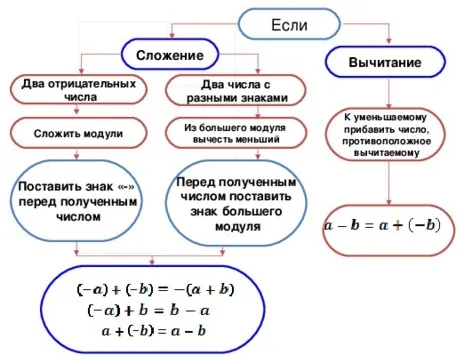
Примеры отрицательных чисел:
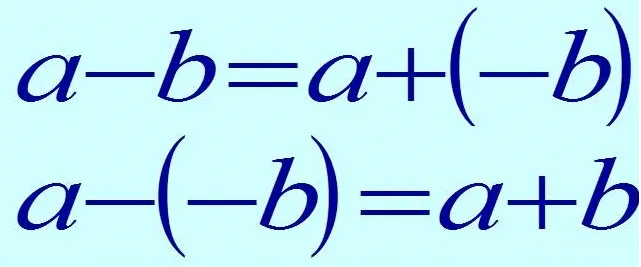
Координатная прямая
Давайте подробнее рассмотрим шкалу термометра и попытаемся схематично ее проиллюстрировать. Шкала представляет собой прямую линию. Давайте нарисуем его:

Обратите внимание, что каждое деление соответствует 1 градусу. Оказывается, что шкала — это единичная линия.

Воспользуемся чертежом единичного деления, не забыв отметить его по обе стороны от базовой линии:
Давайте посмотрим на получившуюся картинку. Построенная геометрическая фигура имеет направление, опорную точку и единичный сегмент. В математике такие фигуры имеют свое название — координатная линия.

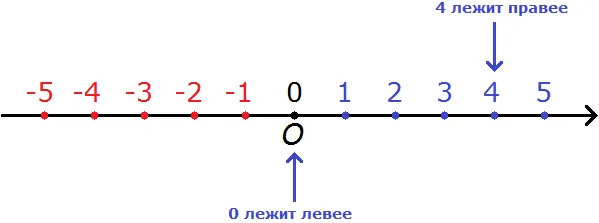
Важно, чтобы на координатной прямой справа от начальной точки (0) располагались положительные числа, а слева — отрицательные (записываются символом «минус»).
Мы начертили координатную линию и отметили на ней числа о т-7 до 7.
На самом деле, на рисунке показана лишь небольшая часть прямой линии. Эта линия продолжается в обоих направлениях до бесконечности, потому что по определению она не имеет ни начала, ни конца.
Координата точки
Каждая точка на прямой линии всегда имеет числовое обозначение или координату.

Рассмотрим пример.
Проведите прямую координатную линию; отметьте начало и выберите единичный отрезок длиной 1 сантиметр. Обозначьте разделение буквой A:
Читает, точка А с координатами 1.
Нет ничего сложного!
Давайте применим полученные знания на практике и решим проблему.
Проведите координатную прямую и укажите точки B(4), C(-2).
Чтобы решить эту задачу, нужно провести линию, выбрать направление, начальную точку и единичный отрезок в 1 см.
Теперь нужно определить точку B с координатами 4. Координата 4 показывает, что точка B находится на расстоянии четырех единичных отрезков от нуля, то есть расстояние от нуля до точки B равно четырем сантиметрам.
Теперь обратите внимание на точку C, которая имеет координат ы-2. Координата отрицательна, т.е. отмечена слева от нуля. Значени е-2 означает, что расстояние от нуля до точки C равно двум сантиметрам.
Помните! Положительные числа всегда находятся справа от нуля, а отрицательные — слева от начала координат. В этом случае нулевой точкой является начало координат.








