Показательные неравенства. Как решать показательные неравенства. Какие неравенства называются показательными.

Иногда эти выражения могут быть очень длинными и запутанными, но пусть это вас не смущает. Почти все неравенства, связанные с функциями с однородными показателями, решаются по одному и тому же принципу: вы пытаетесь упростить выражение, разделив его на один член, а затем при необходимости заменяете переменные.

Показательные неравенства

Экспоненциальные неравенства обычно рассматриваются после введения в экспоненциальные уравнения. Если введение прошло успешно, и вы теперь знакомы с уравнениями, этот материал будет в основном повторением того, что вы уже изучили. Но это не значит, что вы не увидите ничего нового — решение экспоненциальных неравенств имеет свои подводные камни.

— Обновлено 28 октября 2022 года

Определение показательных неравенств

Экспоненциальные неравенства — это неравенства, в которых переменная входит в экспоненту: .

Экспоненциальные неравенства — это неравенства, которые имеют переменные как в экспоненте, так и в основании.

Стоит повторить изучение этой темы:

• показательные уравнения;
• метод интервалов;
• разложение многочлена на множители;
• свойства степенной функции.

И, конечно, для решения смешанных неравенств, включающих тригонометрические и логарифмические неравенства, вам потребуется вспомнить формулы из соответствующих разделов алгебры.

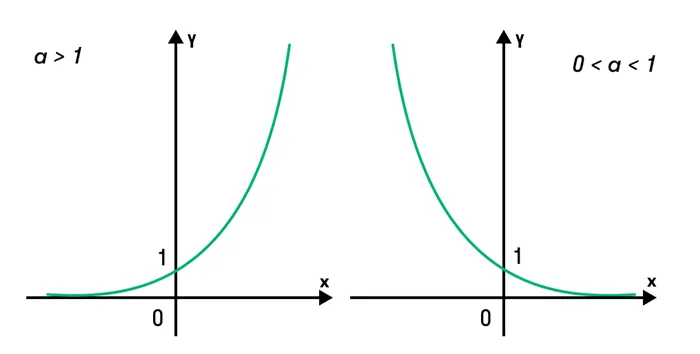
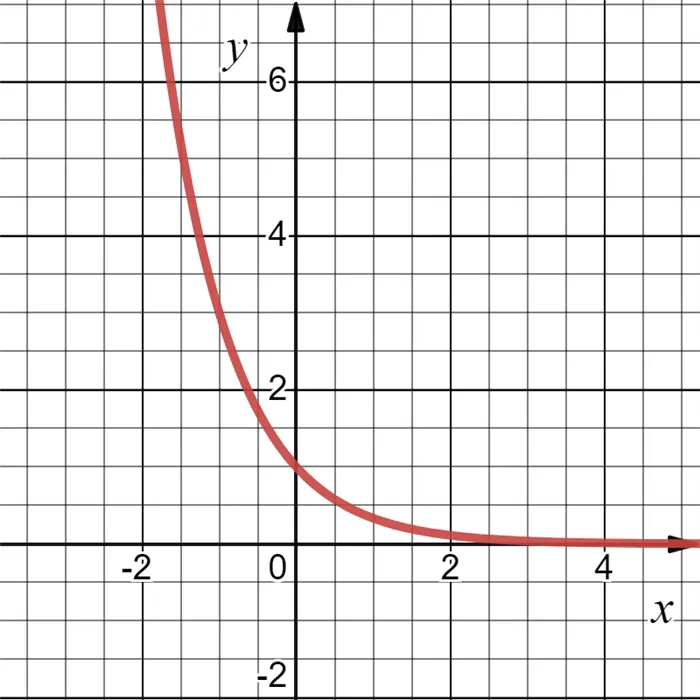
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a x, где a>0 и a ≠ 1. Две приведенные ниже диаграммы дают представление о том, как выглядит такая функция, когда основание степени α положительно, но не равно единице. Вы, наверное, уже догадались, какое самое важное свойство у этой функции. Да, он монотонный.

Однако следует отметить, что его значения всегда больше нуля. На практике в этом можно легко убедиться, умножив любое число (большее нуля) на все возможные силы, включая отрицательные. Например. Значение функции уменьшается, но никогда не достигает нуля.

Для любых а и х верно неравенство a x>0, т.е. экспоненциальная функция не может принимать отрицательные значения.

Запишем непрерывность монотонности экспоненциальной функции в виде формул:

• , когда функция возрастает, т. е. ;
• , когда функция убывает, т. е. .

Все методы решения так или иначе опираются на это свойство экспоненциальных неравенств, и сейчас мы разберемся, как его использовать.

Выясните, в каких темах вы «хромаете», а затем проработайте их без формул и скучных лекций.

Как решать показательные неравенства

Как мы уже говорили ранее, для успешного освоения этой темы вам необходимо хорошо изучить все темы, связанные с уравнениями экспоненты. Способы решения показательных неравенств выглядят практически одинаково — мы пытаемся упростить выражение, получить одинаковые степени или основания, свести все к квадратному или рациональному уравнению, если это возможно. Но есть и свои тонкости.

Допустим, у нас есть простейшее экспоненциальное неравенство:

Если вы помните, как решать показательные уравнения, то вам не придется долго думать, что делать с таким неравенством — сведем его к одному основанию:

Все это звучит логично, но всегда ли безопасно планировать на основе одной и той же степени? Что если вместо 3 у нас будет основание в одну степень 0,5? Давайте посмотрим:

Проверим, верно ли в таком случае х>2.

0,5 3 = 0, 125 и т.д.

Если а>1, то при решении неравенства можно просто вычесть основания той же степени.

Для ясности всегда предполагается, что основание степени является положительным числом.

Это были общие правила, а теперь давайте рассмотрим различные типы показательных неравенств и примеры с решениями.

Курсы подготовки к GCSE по математике от Skysmart придадут вам уверенности и помогут подтянуть знания перед экзаменом.

Показательные неравенства. Как решать показательные неравенства?

Однако при переходе к экспоненциальным неравенствам есть одна важная деталь: \(-\) если основание ступени больше \(1\), знак неравенства должен остаться прежним, \(-\) если основанием является число большее \(0\), но меньшее \(1\) (т.е. находится между нулем и единицей), знак неравенства должен быть обратным, т.е….

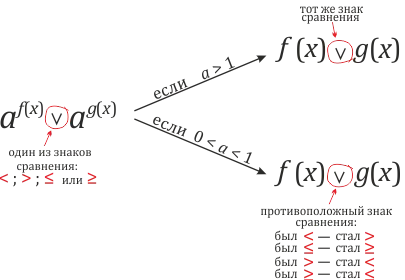
Важно! Существуют две предпосылки для перехода к экспоненциальным неравенствам: \(-\) число вв основании степени\(-\) степени слева и справа должны быть «чистыми», т.е. не должно быть коэффициентов, умножений, делений и т.д.

Переход к \(x+2>8-x \) невозможно, потому что основания имеют разные номера.

Переход к \(5-x≥7x\) невозможен, потому что силы не являются «чистыми» (перед силой справа стоит знак минус).

Пример. Решите экспоненциальное неравенство.Решение:

Вы не можете сделать переход сразу, сумма в левой части не дает. Поэтому мы используемВы не можете использовать правую часть сразу, но мы используем правую часть сразу.и преобразовать \(2^=2^ \cdot 2^2=4 \cdot 2^x\).

Теперь \(2^x\) и \(4 \cdot 2^\)являются аналогичными терминами.мы можем добавить их.

Разделите обе части неравенства на \(5\).

Представьте четыре как \(2^2\).

Вот теперь делаем переход: избавляемся от оснований, не меняя знак сравнения, т.к. основание \(2>1\)

Пример. Решите экспоненциальное неравенство: \(4^-5 \cdot 4^+4<0\)Решение:

Это стандартное экспоненциально-квадратичное неравенство. Преобразуем по свойству мощности \(4^=(4^x)^2\) так, чтобы на следующем шаге мы имелиЗамена.

Изменить переменные

Запишите неравенство в новой форме

Разложите его наМультипликаторыправая сторона

Запишите промежуточное решение следующим образомСистемаи выполнить обратную подстановку

Решение экспоненциальных неравенств

Решение показательных неравенств с разными основаниями

Но что, если невозможно свести левую и правую части неравенства к силам с одинаковым основанием (т.е. в виде \(a^ ˅ a^)\)? Тогда величиелогарифм. Согласно основному логарифмическому тождеству — \(c=a^<\log_<⁡c>>\(5=2^), что означает, что любое положительное число может быть представлено в виде силы с любым основанием.<\log_<2>>\) ; \(0,1=200^<\log_<200>>\) и так далее.

Основания устраняются сменой знака, потому что \(0,2

\(\log_\) — уродливое число, но это все же число, т.е. мы имеем дело с обычным линейным неравенством. Мы выражаем \(x\), перенося \(4\) в правую часть

Разделите обе части на \(-7\).

Реакция:\(x∈\) \(\frac.<4-\log_<0,2>>\(\)\) \(?∞)\) Я знаю, что это выглядит не очень хорошо, но ответ нельзя выбрать.

Особые виды показательных неравенств

Ведь никакая степень не превращает положительное число в отрицательное. Почему бы и нет? Потому чтопоказатель степениговорит только о том, во сколько раз умножается само основание. Основание положительно, а произведение положительных чисел всегда положительно.

Поэтому никакое количество \(x\) не может сделать \(5^x\) отрицательным. То же самое верно для \(2^x\), \(3^x\), \(4^x\), \(6^x\) и т.д.

Если \(a\) – положительно, то \(a^x>0\) при любых \(x\)

Таким образом, экспоненциальное неравенство имеет \(5^x

Рассмотрим обратное неравенство: \(5^x>-5\).

\(5^x\) – всегда больше нуля, и, уж тем более, оно будет больше \(-5\). Значит, решением неравенства \(5^x>-5\) может быть любым числом.

Как приводить степени к одному основанию

Пример 7 $5^x \le 3;$ На первый взгляд, пример похож на предыдущий. Чтобы решить неравенство, нужно свести его к одному основанию. Действительно, но как \(3k\) представляется как мощность \(5k\)?

В этом нет ничего сложного. Оказывается, что любое число \(a\) можно представить в виде степени с нужным основанием \(b\). Но без логарифмов не обойтись. Это можно сделать с помощью формулы.<\log_ (a)>; \qquad (*)$ Например: \(3=5^<\log_<5>(3)>;\)

Если вы забыли, что такое логарифмы, вам обязательно нужно посмотреть их здесь.

Мы уже использовали эту формулу в главе об уравнениях экспоненты. Чтобы решать неравенства, вам не нужно разбираться в них, вы можете просто подставить числа в формулу. Но я бы рекомендовал вам понимать все, что вы используете. Поэтому подумайте сами, почему эта формула верна.

Рассмотрим правую часть формулы (*): В силе — логарифм \(\log_(a)\). Логарифм — это число, которое мы должны перевести в основание \(b\), чтобы получить \(a\). И, наконец, в правой части формулы (*) мы получаем \(b\) в степени, до которой \(b\) нужно поднять, чтобы получить число \(a\). Вот как работает эта формула, которая немного запутана. Но если подумать, все не так уж сложно.

Вернемся к примеру 7. Теперь мы знаем, как представить \(3k\) в виде степени \(5k\): $3=5^<\log_(3)>$ Замените $5^x \le 5^<\log_(3)>$ Наши основания равны, поэтому убираем $x \le \log_(3);$ Ответ остается уродливым логарифмом. Мы не можем рассчитать его без калькулятора. Мы сделаем это в тесте.

Пример 8 $\left(\frac\right)^ А значит, \(5^x>0\) и никак не может быть меньше \((-3)\), какие бы \(x\) вы не подставляли. Попробуйте подставить вместо \(x\) минус миллион, что вы получите? По определению отрицательной степени: $a^=\frac;$ $ 5^=\frac>Несомненно, это будет очень небольшое, но положительное число. Поэтому в данном примере корней нет. Помните об этом.

Пример 10 $ 7^x>-6;$ Неравенство, аналогичное примеру 9, но с другим знаком неравенства. Что изменилось? Теперь нам нужно найти число \(x\) такое, чтобы экспоненциальная функция \(7^x\) была больше отрицательного числа \((-7)\). Но поскольку экспоненциальная функция больше \(0\) для любого \(x\), то она, конечно, уже больше \((-7)\). Что бы вы ни заменили, вы всегда получите правильное неравенство. Ответ — любое число.

Теперь давайте рассмотрим немного более сложный пример. Пример 11 $ 25^-0.2^ \le 0;$ Попробуйте выполнить это неравенство точно так же, как в предыдущих примерах. Для этого сдвинем вторую сумму \(0,2^\) вправо: $ 25^ \le 0,2^;$ Сведем ее к одному основанию. Я рекомендую записывать десятичные дроби в виде дробей, чтобы вы могли сразу увидеть, к какому основанию их имеет смысл сокращать: $0,2=\frac=\frac;$$ 25^ \left(\frac

Замена в показательных неравенствах

ight)^;$ Left и right — это числа, которые легко представить в виде силы \(5-ki\): $25=5^2;$ $ $ \frac=5^;$ Замените $ (5^2)^ \le (5^)^;$ $ $ 5^ \le 5^;$ $ $ 5^ \le 5^;$ Основания одинаковые, оставьте их: $ 2x^2-4x+20 \l e-2x^2+4x+80? $ $4x^2-8x-60 \le 0;$ Разделите квадратичный многочлен по дискриминанту на кратные: $ 4(x+3)(x-5) \le 0;$ И решите с помощью пространства:

Мы разобрали все типы простых силовых неравенств. Основываясь на этих знаниях, мы можем перейти к более сложным неравенствам, которые решаются путем замены переменной. Такие примеры довольно часто встречаются в GCSE по математике.

Если в прошлом вы решали уравнения или неравенства с заменой переменных, это не должно вызвать затруднений. Давайте рассмотрим несколько примеров:

Пример 12 $ 4^x-29*2^x+168\le 0. $ Следуя обычной логике экспоненциальных неравенств, вы сводите все экспоненциальные функции к одному основанию. Это легко сделать здесь: $ (2^2)^x-29*2^x+168 \le 0$ $ 2^-29*2^x+168 \le 0$ Готово. Теперь обратите внимание, что \(2^=(2^x)^2\) согласно свойству мощности. Подставим: $(2^x)^2-29*2^x+168 \le 0$ В каждом примере замены переменной нужно найти одинаковые конструкции (выражения), которые зависят от \(x\). В нашем примере есть такая структура — \(2^x\).

Обозначим \(t=2^x\) и подставим наше неравенство: $ t^2-29t+168 \le 0 $ В итоге мы имеем общее квадратичное неравенство, которое я обычно решаю методом универсального интервала: $$=29^2-4*168=841-672=169;$$t_=\frac=21;$$t_=\frac=8;$ Зная корни, разложим квадратичный многочлен на кратные: $(t-8)(t-21)\le 0;$ Для метода интервалов проведем числовую линию, запишем нули функции (корни) и исследуем интервалы. Для тех, кто не помнит метод интервалов, рекомендую повторить его; без него решение экспоненциальных неравенств бессмысленно.

Получаем интервалы для переменной \(t\): $ t \in 8;21;$ А вот распространенная ошибка, из-за которой студенты перестают решать здесь. Однако в задаче спрашивается не \(t\), а \(x\)!

Поэтому необходимо сделать обратную подстановку, чтобы вернуться к исходной переменной \(x\). Для этого мы используем простую логику: поскольку \(t\in8;21\), то \(t\) может принимать значения больше или равные 8, но не больше 21. Запишем то же самое в виде системы (системы, потому что эти условия должны выполняться одновременно): $ \begin t \begin 8, \begin t \begin 21.\end$ Теперь нам нужно вспомнить, что такое \(t\). Это та переменная, для которой мы вызвали \(2^x=t\). Заменим \(2^x\) на \(t\).<\log_(21)>Обратная подстановка: $ \begin 2^x \ge 8, \\\ 2^x \le 21. \end$ Мы получили систему двух простых неравенств с экспонентой, которые уже научились решать выше. $ \begin 2^x \ge 2^3, \\ 2^x \le 2^

. \end$ Базы везде одинаковые, от них можно избавиться.

Как видите, все не так уж сложно. Рассмотрим другие примеры замены переменных в показательных неравенствах.

Пример 13 $ 2^x+6*2^ \le 7$ Этот пример также является подстановкой. Хотя основания экспоненциальных функций одинаковы (два), они имеют разную мощность, поэтому мы пока не можем выполнить замену. Мы должны сделать все одинаковым — степени и основания.

Однородные показательные неравенства

Вспомните свойство мощностей с отрицательной экспонентой: $a^=\frac;$ и примените его к нашему неравенству: $ 2^x+6*\frac \le 7$ Обозначим через \(t=2^x\) и подставим: $ t+6*\frac \le 7$ Чтобы применить здесь метод интервалов, нужно перевернуть все слева и привести к общему знаменателю. $ \frac \le 0$ Я не рекомендую опускать знаменатель в неравенствах, как это принято делать в уравнениях. Для подавляющего большинства неравенств этого делать не следует, так как это также влияет на знак всей функции. Это одна из самых распространенных ошибок в США. Вот почему я рекомендую всегда включать знаменатель в уравнение, а не вычитать его. Подробнее об этом можно прочитать в теории обыкновенных неравенств.

Теперь мы рассмотрим другой тип показательных неравенств — однородные неравенства. Такие неравенства часто возникают, когда мы имеем много экспоненциальных функций с разными основаниями, и свести их к одному основанию не представляется возможным. Как обычно, давайте сразу перейдем к конкретному примеру.

Пример 17 $25^x-20^x-2*16^x \le 0$ Что примечательного в этом уравнении? Попробуем наш старый алгоритм свести все к одному основанию. $25^x=5^;$$20^x=(5*4)^x=5^x*4^x;$$16^x=4^;$ Как видите, мы не можем свести к одному основанию. Невозможно использовать те же функции экспоненты, когда основания равны 5 и 4. Мы будем работать с тем, что у нас есть. Подставим полученное разложение в исходное неравенство. $5^-5^x*4^x-2*4^ \le 0;$

Разобьем левую часть на несколько дробей. То есть, поделим каждый одночлен числителя на знаменатель дроби. В правой части, очевидно, получается 0. $\frac>>-\frac>-2*\frac>>\le 0;$ $1-\frac-2*\frac>>Поскольку неравенства можно делить на положительные числа, разделим полученное неравенство на \(5^\). К лучшему или худшему, напомню, что деление неравенств на положительные числа полностью делит как левую, так и правую часть неравенства, за исключением того, что в данном случае преобразование эквивалентно, а значит, корни не меняются. Вы можете разделить неравенство на \(5^\), потому что это экспоненциальная функция, которая по определению всегда строго больше нуля.<\log_<\left(\frac\right)>(\frac)>\le 0;$ $1-\left(\frac<\left(\frac\right)>ight)^x-2*\left(\frac

ight)^ \le 0? $ 1-\left(\frac

ight)^x-2*\left(\frac

ight)^ \le 0, $ После некоторых преобразований деления мы получаем экспоненциальную функцию \(\left(\frac

ight)^x\) везде, которую можно смело заменить на \(t=\left(\frac

Алгоритм решения

ight)^x\). $1-t-2*t^2 \le 0;$ $-2*t^2-t+1 \le 0;$ Разложим квадратичный многочлен на коэффициенты с помощью дифференцируемости, вспомнив коэффициент \(-2\). $-2(t+1)(t-\frac) \le 0;$ Решение этого квадратичного неравенства: $ t \in (-\infty;-1\in\frac;+\infty);$ Перепишем пробел как количество. \ \ \end

ight.$ А теперь мы сделаем это в обратном порядке. Помните \(t=\left(\frac

• уединение слагаемого, содержащего неизвестную для левой и правой стороны;
• приведение степени к общему основанию;
• упрощение выражений с использованием свойства степеней и модулей, метода объединения членов;
• решение полученного неравенства.

ight)^x\): $\left \begin \left(\frac

В зависимости от типа неравенства используют различные приёмы. Если уравнение относится к виду n f ( x )>m d ( x ), то выражение пытаются преобразовать к такому виду, чтобы основания стали степенями одного и того же значения. То есть n = p w, m = p k. После чего решают простейшие неравенства вида: p wf ( x )>ight)^x \l e-1, \left(\frac

ight)^x \ge \frac. \end

ight.$ \begin \left(\frac

• она возрастает, когда m>1;
• график убывает, если выполняется условие: 0
• если y>0, функция принимает только положительные значения.

Для успешного выполнения самостоятельных работ необходимо запомнить, что если основание больше единицы, то неравенству: m f(x )>m s(x), равносильно: f(x)>ight)^x \l e-1, \\\\left(\frac

Простейшие примеры

ight)^x \ge \left(\frac

Например, нужно решить неравенство вида: 8 P>0,25. Для нахождения множества решений уравнение переписывают следующим образом: (2 3 ) p>25/1000. Правую часть можно сократить на 25 в итоге она упростится до простой дроби 1/40. После дальнейшего преобразование неравенство примет вид: (2 3 ) p>ight)^^

Так как функция вида 2 f ( x ) является возрастающей, то график при переходе от одной части неравенства к другому знак не изменяет. Используя правило, выражение можно переписать как 3*p>5,3. Отсюда p>. \ \end

ight.$\left \begin \left(\frac

ight)^x \l e-1, \³ x \ge \log_

Сложные задания

(\frac_.) \ \end

ight.$ Первое неравенство вообще не имеет решений, так как экспоненциальная функция всегда больше нуля, поэтому еще больше \(-1\).

Если нет возможности свести все функции неравенства к одному основанию, попробуйте решить уравнение делением как однородное уравнение. Разные основания указывают на то, что пример может быть решен делением.

Давайте рассмотрим еще один интересный пример с разными основаниями. Только это уже не однородное уравнение.

Пример 18 $6^x-4*3^x-2^x+4 \le 0$ Обратите внимание, что в неравенстве 4 члена. Четное количество слагаемых иногда указывает на метод группировки. Эта тема изучается в 8 классе, но если вы ее не помните, вы можете выучить ее сейчас на этом примере.

• от — ∞ до 1/2 знак будет положительным;
• в интервале от 1/2 до логарифма отрицательным;
• от логарифма до ∞ снова плюсовым.

Сначала сгруппируйте суммы попарно — первую со второй и третью с четвертой. Затем вычтите общий коэффициент. Первое и второе слагаемые имеют общий множитель \(3^x\), а третье и четвертое слагаемые имеют общий множитель \(-1\).

В принципе, решение показательных неравенств ничем не отличается от нахождения ответа на аналогичные уравнения. Существует два метода: графический и аналитический. В первом методе необходимо построить графики двух функций. То есть, вы строите левую и правую части в декартовой системе координат, а затем определяете точки пересечения графиков с осью абсцисс.

Уравнения с заменой переменных

Для простых функций (квадратичных) графическое решение может быть довольно удобным способом, но для выражений с более высокой степенью использовать этот метод неудобно. Поэтому используется аналитический подход. Он основан на:

То есть предполагается, что две части выражения имеют определенное отношение друг к другу на одном и том же основании. Метод повторяет алгоритм нахождения корней в уравнениях. Но в отличие от них, ищутся не определенные числа, а интервал.

p k d ( x ) .

Другим методом является разделение на множители, а также подстановка переменной. В последнем случае неравенство экспоненты сводится к простому, обычно квадратичному неравенству, в соответствии с которым решается обратная подстановка.

Все методы решения экспоненциальных неравенств основаны на поведении функции y = m x, т.е:

s(x). В случае, когда 0

Чтобы научиться решать сложные задачи, вы должны уметь самостоятельно решать элементарные неравенства. Поэтому вы должны практиковаться в вычислении таких простых задач самостоятельно.

2 5,3 .

5,3/3. Ответ на этот вопрос лежит в диапазоне от 1,76 до плюс бесконечности.

Другие проблемы аналогичного характера решаются с помощью аналогичного алгоритма. Например, необходимо решить неравенство: 0,5 3x+4 ≥ 4. В начале вы должны попытаться свести обе части к одной основе. Если уравнение имеет мощность с десятичным основанием, необходимо попытаться преобразовать ее в обычную мощность.

Основание 0,5 можно представить как 1/2, а квадрат — как два в квадрате или (1/2) -2. Тогда неравенство имеет вид (1/2) 3x+4 ≥ (1/2) -2. Поскольку основание 1/2 больше нуля, но меньше единицы, знак в уравнении меняется на противоположный. Полученное неравенство имеет вид: 3x+4 ≤ -2. После группировки однородных членов справа и слева получается выражение: x ≤ -2. Это и есть ответ на задачу. Его также можно записать как x є (- ∞;-2 ).

Не всегда можно свести задачу к неравенству, в котором числа равны друг другу. Такие задачи решаются методом интервалов. Его удобно использовать, когда числитель и знаменатель — степени, а неравенство имеет вид: f (x)/ s(x) ≥ 0.

Например, нужно решить неравенство (2*3 2x+1 )-6x- 4x- 1-9)/(9 x-3) ≤ 3. Сначала нужно решить произведение: 3 2x+1 = 3 2x * 3 1 = 9 x. Затем тройка в правой части удаляется путем деления на нее обеих функций. В результате получается следующее уравнение: (2*3*3 2x 2x -(2*3) x-4*4 x-9)/(9 x-3)-(3/1) ≤ 0. Упростив выражение путем раскрытия скобок и объединения подобных членов, его можно свести к виду (3*3 2x 2x — 2 x *3 x-4*2 2x )/(3 2 x-3) ≤ 0.

Теперь мы можем перейти к методу интервалов. Для этого числитель и знаменатель должны быть установлены на ноль. Начните с числителя: 3*3 2x 2x — 2 x *3 x-4*2 2x = 0. Это однородное выражение, где каждый член кратен 2 2 x. В результате получается сложный квадратичный многочлен: 3*((3 / 2) x ) 2 -(3/2) x-4 = 0. Необходимо вычислить его корни. Это лучше всего сделать, найдя определитель. Решением является логарифм по основанию 3/2 минус один.

Теперь посмотрим на знаменатель, так как он не должен быть нулевым: 3 2 x-3 ≠ 0. Решив неравенство, мы можем найти, что x ≠ 1/2.

Затем сравните первый и второй найденные ответы и определите, какой из них больше, чтобы определить области решения на числовой прямой. Чтобы определить принадлежность знака к множеству, нужно взять любое число из каждого полученного диапазона и подставить его в задачу. Результат будет выглядеть следующим образом:

Согласно заданию, неравенство должно быть меньше или равно нулю. Поэтому окончательный ответ записывается как x є (1/2; Log3/2 2-1 ).

Графическое решение показательных уравнений

Вычисление сложных уравнений требует дедукции и тщательности. Часто это занимает довольно много времени.

В некоторых случаях для решения экспоненциального уравнения необходимо ввести новую переменную. В задачах, которые вам предлагается решить, это обычно, но не всегда, приводит к квадратному уравнению.

Задание. Решите уравнение, подставив переменную.

Обратите внимание, что в уравнении есть степени 3 и 9, но 3 2 = 9. Затем введите новую переменную t = 3 x. Если мы возведем его в квадрат, то получим

Таким образом, исходное уравнение можно переписать:

Получаем обычное квадратное уравнение. Решите ее:

Мы нашли два значения t. Тогда мы должны вернуться к исходной переменной, а именно x :

Первое уравнение не имеет решений, потому что экспоненциальная функция может принимать только положительные значения. Поэтому нам нужно рассмотреть только второе уравнение:

Задание. Найдите корни уравнения

Решение. Здесь мы имеем три экспоненциальные функции в одном уравнении. Давайте попробуем упростить ситуацию и избавиться от одного из них. Для этого разделите уравнение на 4 4x+1:

Поскольку 1 4x+1 = 1, мы можем записать:

Показательные неравенства

Рассмотрим координатную плоскость, в которой построен график некоторой показательной ф-ции у = а х, причем а>Обратите внимание, что делить уравнение на выражение с одной переменной можно только в том случае, если мы уверены, что оно не обратится в ноль при любом значении x. В этом случае мы можем быть уверены, что оно выполняется, так как 4 4x+1 строго положительно для любого x.

Вернемся к уравнению. Он содержит наборы (9/4) 4x+1 и (3/2) 4x+1. У них одинаковая экспонента, но разные степени. Однако можно заметить, что

9/4 = (3/2) 2, поэтому также (9/4) 4x+1 = ((3/2) 4x+1 ) 2. Это означает, что это уравнение с заменой переменных.

Если подставить t = (3/2) 4x+1, то (9/4) 4x+1 = ((3/2) 4x+1 ) 2 = t 2. Затем мы перепишем уравнение с новой переменной t:

Снова получаем квадратное уравнение.

Давайте еще раз вернемся к переменной x:

Здесь также первое уравнение не имеет корней, так как экспоненциализация положительного числа не приводит к отрицательному. Остается решить второе уравнение:

Не каждое экспоненциальное уравнение может быть решено легко или даже аналитически. В таких случаях помогает графическое решение уравнений.

Задача. Найдите значение x, для которого уравнение имеет видРешение. Построим y = 3 x и y = 4 — x в той же системе координат:

Оказывается, что графики пересекаются примерно в одной и той же точке с координатами (1; 3). Поскольку график не совсем точный, следует подставить x = 1 в уравнение и убедиться, что это действительно корень уравнения:

Равенство верно, поэтому x = 1 действительно является корнем уравнения.

Задача. Решите уравнение графически

Решение. Переместите все члены, кроме 2 x, вправо:

Слева находится экспоненциальная функция, а справа — квадратичная. Постройте их графики и найдите точки пересечения:

Мы видим, что графики имеют две общие точки, а именно (0;1) и (1;2). Мы можем проверить это, подставив x = 0 и x = 1 в исходное уравнение:

Ноль подходит. Мы проверяем один:

Это тоже подходит. В итоге мы имеем два корня, 0 и 1.

0. Предположим, что значения s и t откладываются на оси Ох, а t.

Очевидно, что точкам t и s на оси Ох соответствуют точки t и s на оси О.

является возрастающей функцией, то значение a t меньше, чем a s. Другими словами, t в O находится ниже s (как показано на графике). Видно, что по условию t

С помощью этого правила мы можем решить некоторые элементарные экспоненциальные неравенства. Например, если нейро

Аннотация к презентации

Представим восьмерку в виде степени двойки:

Согласно только что упомянутому правилу, мы можем заменить этот нерв другим, эквивалентным ему:

Решением этого линейного неравенства является интервал (- ∞; 3).

Аннотация урока

Однако сформулированное нами правило работает, когда основание экспоненциальной функции больше единицы. Но что происходит, когда число меньше единицы? Нарисуем такую функцию и снова построим графики t и s в Ω. Опять же, t меньше s, т.е. эта точка находится слева.

Поскольку экспоненциальная функция y = a x уступает по основанию меньше единицы, то a s оказывается уступающей a t на оси O. Таким образом, по условию t

а с. Оказалось, что эти нервы эквивалентны.

Альберт Эйнштейн

Например, решим экспоненциальное неравенство

Выразите число слева в виде степени 0,5:

Структура урока

Тогда нейро имеет вид

Согласно только что рассмотренному правилу, его можно заменить эквивалентным нервом

Организационный момент

В наиболее распространенной форме, когда выражение с одной переменной находится в левой части, нейронная машина выглядит следующим образом

и его решением является интервал (3; + ∞).

Постановка целей и задач

В общем случае можно утверждать, что если экспонента нерва имеет вид

основание a больше единицы, его можно заменить эквивалентным нервом

Цели урока

Грубо говоря, мы просто удаляем основание силы, а знак нерва остается неизменным. Если основание α меньше единицы, то знак неравенства должен быть обратным:

Это правило также применяется, когда вместо чисел или переменных t и s используются произвольные функции f(x) и g(x):