Получить этот конус несложно. Возьмите правильный треугольник, положите его на один из зондов и вращайте его вокруг второго зонда, который является осью, а длина — высотой для объемной фигуры. Зонд, на котором стоит треугольник, является радиусом кругового основания конуса.
Площадь поверхности усеченного конуса
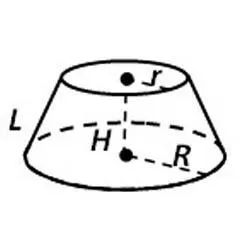
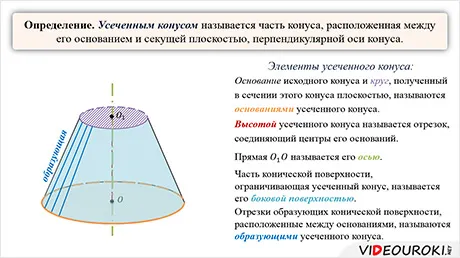
Конус — это часть конуса, которая лежит между двумя параллельными основаниями, перпендикулярными его оси симметрии. Основания конуса представляют собой геометрические круги. Усеченный конус получается при вращении прямоугольной трапеции вокруг своей стороны, которая является ее высотой. Границей конуса является окружность радиуса R, окружность радиуса r и боковая поверхность конуса. Боковая поверхность конуса описывается боковой поверхностью трапеции при ее вращении.
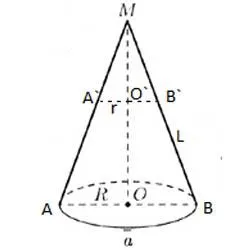
При нахождении площади боковую поверхность усеченного конуса целесообразней рассматривать как разность боковой поверхности конуса и боковой поверхности отсеченного конуса. Пусть от данного конуса AMB отсекли конус A`MB`. Необходимо вычислить боковую площадь усеченного конуса AA`B`B. Известно, что радиусы его оснований AO=R, A`O` = r, образующая равна L .Обозначим MB` за x. Тогда боковая поверхность конуса A`MB` будет равна πrx. А боковая поверхность конуса AMB будет равна πR(L+x). Тогда боковую поверхность усеченного конуса AA`B`B можно выразить через разность боковой поверхности конуса AMB и конуса A`MB` : rx=(RL+Rx-rx)=(RL+x(R-r))» />Треугольники OMB и O`MB` – подобны по равенству углов ∠ = ∠ и ∠ = ∠. Из подобия этих треугольников следует: Воспользуемся производной пропорции. Имеем: Отсюда находим x : » />Подставив это выражение в формулу площади боковой поверхности, имеем: />(R-r) )=(RL+rL)=L(R+r)» />Поэтому боковая площадь усеченного конуса равна произведению π-кратной проводимости и суммы радиусов его оснований. Формула для боковой площади усеченного конуса выглядит следующим образом:
Пример расчета площади боковой поверхности усеченного конуса, если известны его радиус и образующая Радиус большего основания, образующая и высота усеченного конуса равны 7, 5 и 4 см соответственно. Найдите площадь боковой поверхности конуса. Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют египетский треугольник. Это прямоугольный треугольник с соотношением сторон 3:4:5. По условию задачи образующая равна 5, а высота – 4, тогда разность радиусов основания усеченного конуса будет равна 3. Имеем: L=5 R=7 R=4 Формула площади боковой поверхности усеченного конуса имеет следующий вид: Подставив значения, имеем: » />
Площади боковой поверхности усеченного конуса через направляющую и средний радиус
Средний радиус усеченного конуса равен половине суммы радиусов его оснований: Формула для боковой площади усеченного конуса может быть представлена следующим образом: Боковая площадь усеченного конуса равна произведению окружности центральной части и его формы.
Если меньшее основание ортогонально спроектировать на большее основание, то тогда проекция боковой поверхности усеченного конуса будет иметь вид кольца, площадь которого вычисляется по формуле: (R-r)(R+r)» />Тогда: />» />
Площади боковой поверхности усеченного конуса по Архимеду
)^2″ />Боковая площадь усеченного конуса равна площади такого круга, радиус которого равен произведению среднего модуля и суммы радиусов его основания.
Общая площадь конуса равна сумме площади его боковой поверхности и площади основания конуса:
» />
Основаниями конуса является круги с радиусом R и r. Их площадь равна произведению числа на квадрат их радиуса: R^2″ />r^2″ />Площадь боковой поверхности вычисляется по формуле: Тогда площадь полной поверхности усеченного конуса равна: R^2+r^2=(R^2+(R+r)L+r^2)» />Формула имеет следующий вид:
Пример расчета площади полной поверхности усеченного конуса, если известны его радиус и образующая Радиус основания усеченного конуса 1 и 7 дм, а диагонали осевого сечения взаимно перпендикулярны. Найдите площадь полную площадь усеченного конуса Осевое сечение усеченного конуса представляет собой равнобедренную трапецию, с основаниями 2R и 2r. То есть основания трапеции равны 2 и 14 дм соответственно. Так как диагонали трапеции взаимно перпендикулярны, то высота равна полусумме ее оснований. Тогда: Образующая усеченного конуса, являющаяся боковой стороной трапеции, высота, опушенная на большое основание и разность радиусов основания усеченного конуса, образуют прямоугольный треугольник. По теореме Пифагора найдем образующую усеченного конуса: =sqrt=sqrt=10″ />Формула площади полной поверхности усеченного конуса имеет следующий вид: Подставив значения из условия задачи и найденные значения, имеем: (49+80+1)=130″ />
Нахождение площади поверхности усеченного конуса: формулы
В данной статье объясняются формулы для вычисления площади поверхности прямолинейного кругового усеченного конуса (площадь боковой поверхности, общая площадь и площадь основания) и приводится пример решения для закрепления теоретического материала.
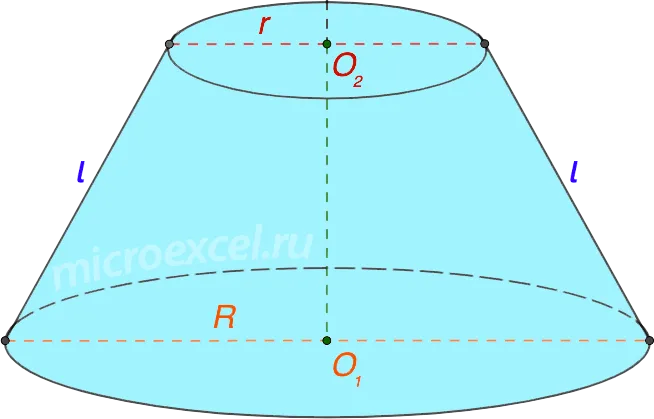
Примечание: Иногда усеченный конус также называют конусным слоем.
1. Боковая поверхность
Чтобы определить площадь (S) боковой поверхности прямолинейного кругового усеченного конуса, необходимо знать длину его основания и радиусы двух оснований.
Примечание: В этой и других формулах, приведенных ниже, число π обычно округляется до 3,14.
2. Основания
Основаниями кругового фрастума являются два круга, площади которых вычисляются таким образом:
Примечание: Если вместо радиусов ( R или r ) указаны соответствующие диаметры ( d ), то для получения требуемых радиусов их следует разделить на 2.
3. Полная площадь
Чтобы вычислить общую площадь усеченного конуса, сложите площади боковых граней двух оснований.
Sвсего.= πl(R + r) + πR 2 + πr 2 = π(lR + lr + R 2 + r 2 )
Пример задачи
Найдите площадь конуса, если известно, что радиусы его оснований равны 6 и 11 см, а длина его формы равна 8 см.
Решение
Мы знаем все известные значения для вычисления площади, поэтому нам остается только подставить их в вышеприведенные формулы.
SБок.= 3,14 ⋅ 8 см ⋅ (6 см + 11 см) = 427,04 см 2
SБаза 1= 3,14 ⋅ (11 см) 2 = 379,94 см 2
SБаза 2= 3,14 ⋅ (6 см) 2 = 113,04 см 2
Sвсего.= 427,04 см 2 + 379,94 см 2 + 113,04 см 2 =
Публикации по теме:
- Нахождение площади круга: формула и примеры
- Нахождение площади ромба: формула и примеры
- Нахождение площади трапеции: формула и примеры
- Нахождение площади параллелограмма: формула и примеры
- Нахождение площади эллипса: формула и пример
- Нахождение периметра треугольника: формула и задачи
- Нахождение периметра прямоугольника: формула и задачи
- Нахождение периметра ромба: формула и задачи
- Нахождение периметра трапеции: формула и задачи
- Теорема синусов для треугольника: формула и задачи
- Теорема о сумме углов треугольника: формула и задачи
- Нахождение объема цилиндра: формула и задачи
- Нахождение объема куба: формула и задачи
- Нахождение объема шара: формула и задачи
- Нахождение объема пирамиды: формула и задачи
- Нахождение объема параллелепипеда: формула и задачи
- Нахождение площади поверхности куба: формула и задачи
- Нахождение радиуса шара: формула и примеры
- Нахождение радиуса круга: формула и примеры
- Нахождение площади прямоугольного параллелепипеда: формула и пример
- Нахождение площади правильной призмы: формула и задачи
- Формула Герона для треугольника
- Теорема Менелая: формулировка и пример с решением
- Теорема Фалеса: формулировка и пример решения задачи
- Свойства прямоугольного треугольника
- Свойства равнобедренного треугольника: теория и задача
- Свойства равностороннего треугольника: теория и пример задачи
- Определение и свойства медианы равностороннего треугольника
- Определение и свойства биссектрисы угла треугольника
- Свойства биссектрисы равнобедренного треугольника
- Определение и свойства высоты треугольника
- Формулы для нахождения высоты треугольника
- Свойства высоты равнобедренного треугольника
- Свойства высоты прямоугольного треугольника
- Нахождение радиуса описанной вокруг квадрата окружности
- Что такое ромб: определение, свойства, признаки
- Нахождение радиуса вписанной в ромб окружности
- Что такое окружность: определение, свойства, формулы
- Нахождение площади сегмента круга
- Что такое параллелограмм: определение, свойства, признаки
- Что такое трапеция: определение, виды, свойства
- Свойства равнобедренной (равнобокой) трапеции
- Что такое средняя линия треугольника
- Что такое куб: определение, свойства, формулы
- Что такое шар (сфера): определение, свойства, формулы
- Нахождение площади шарового сегмента
- Нахождение объема шарового слоя
- Что такое конус: определение, элементы, виды
- Основные свойства конуса
- Нахождение объема усеченного конуса
Как вычислить площадь усеченного конуса
Формула для расчета боковой поверхности усеченного конуса отличается от формулы для расчета прямого конуса.
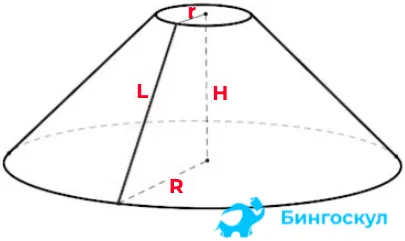
Формула для общей площади поверхности усеченного конуса имеет вид
S1и С2— площадь поверхности усеченного конуса.
Вставьте значения и упростите:
S = π(r 2 + (r + R)l + R 2 .
Учитывая радиусы — 6 и 10 см, расстояние от вершины до точки — 12 см, найдите площадь поверхностей.
S = π * (6 2 + (6 + 10) * 12 + 10 2 ) = 328π ≈ 1030,4 см 3 .
Объем усечённого конуса
Объем — это пространство, занимаемое геометрическим телом. Числовое значение указывает на количество кубиков с единичной гранью, которые помещаются в конус. Объем тела рассчитывается как одна треть произведения площади его основания и высоты.
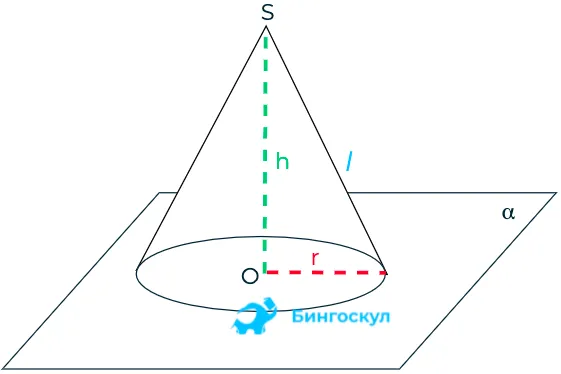
Базовой областью является круг, площадь его поверхности рассчитывается по формуле.База= πr 2. После подстановки получаем:
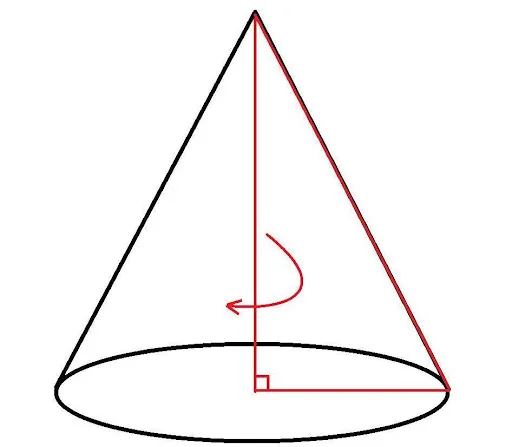
.
Пример: Вычислите объем тела: r = 6 см, h = 9 см. Подставьте значения в формулу и упростите выражение шаг за шагом.
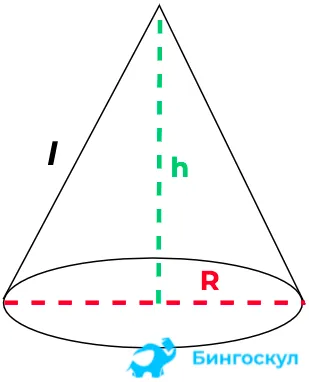
Если диаметр известен, разделите его на два:.
Вычислите объем усеченного конуса. Чтобы понять это, нужно вычесть из общего объема исходного тела ту величину, которая отсекается плоскостью, параллельной дну.
Формула для объема усеченного конуса:
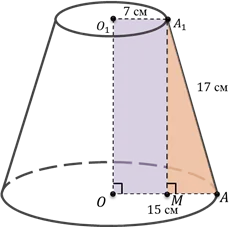
Высота
Существует несколько способов определения высоты усеченного конуса. Выбор подходящего метода зависит от исходных данных.
Если даны радиусы основания и объем, то этого достаточно для выполнения вычислений:

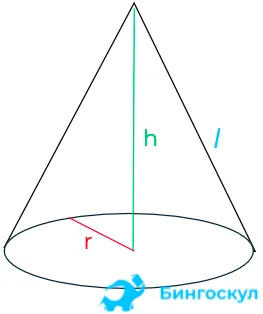
Для прямой линии с известным радиусом или диаметром основания с модулятором можно использовать теорему Пифагора:








