Какие два треугольника называются родственными треугольниками? Возьмите два треугольника ABC и A1B1C1где угол A равен углу A1угол B равен углу B1а угол C равен углу C1.
Планиметрия. Страница 4
Параллелограмм — это геометрическая фигура, диагонали которой пересекаются в точке, делящей ее пополам, а противоположные стороны параллельны.
Теорема: Если диагонали четырехугольника пересекаются и разделены точкой пересечения посередине, то такой четырехугольник называется параллелограммом.
Доказательство. Пусть ABCD — заданный четырехугольник. Точка O является точкой пересечения диагоналей (рисунок 1). Тогда треугольники Δ AOD и Δ BOS равны по двум сторонам и углу между ними. Поэтому угол ODA равен углу CBO, а угол OAD равен углу BCO. Таким образом, эти углы являются внутренними пересечениями прямых AD и BC и прямой AC. Согласно принципу параллельности, AD и BC параллельны. Таким же образом можно доказать, что AB параллельна BC. Теорема доказана.
Рисунок 1 Теорема. Параллелограмм.
Теорема. Если четырехугольник является параллелограммом, то его диагонали пересекаются в точке пересечения.
Доказательство. Рассмотрим параллелограмм ABCD. (Рисунок 2).
Тогда стороны AD и BC равны и лежат на параллельных прямых a и b. Если провести боковые прямые c и d так, чтобы прямая c проходила через A и C, а d — через B и D, то угол OAD будет равен углу OBC, а угол ODA — углу ABK, как внутренние диагональные углы. Таким образом, треугольники AOD и BOS равны по сторонам и прилежащим углам. Из этого следует, что стороны этих треугольников равны. То есть AO = OS и BO = OD. Сумма этих сторон — диагонали параллелограмма.
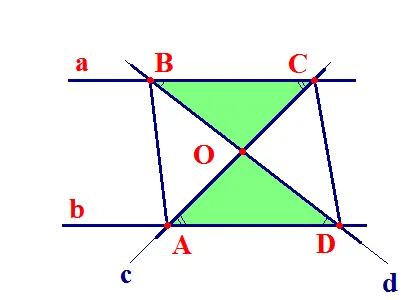
Рис.2 Теорема. Свойство диагоналей параллелограмма.
Ромб
Ромб — это геометрическая фигура, у которой все стороны равны.
Теорема. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Доказательство. Пусть ABCD — ромб. Тогда треугольник ABC равнобедренный. Это означает, что отрезок ОН, составляющий половину диагонали, является биссектрисой диаметра и высоты. Поэтому диагонали ромба AC и BD пересекаются под прямым углом.
Рисунок 3 Теорема. Свойство диагоналей ромба.
Задача
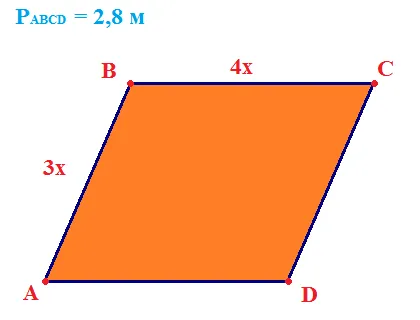
В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке E. Найдите отрезки BE и EC, если AB = 9 см, AD = 14 см (рис. 4).
Решение. Поскольку прямая AE является биссектрисой, это означает, что треугольники ABE и AER равны. Поскольку угол BAE равен углу AER, а угол EAR равен углу BEA как внутренние кресты. Следовательно, ABE — ромб, так как угол BAE равен углу EAR (по условию). Поэтому AB = BE = 9 см и EE = 5 см.
Педагогические и психологические аспекты подготовки школьников к сдаче ГИА
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курс «Инфоурок»).
В настоящее время в общей сложности 54 252 школы и колледжа имеют право на накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учебного заведения, войдите в личный кабинет Инфоурок.
Курс переподготовки
Педагогическая деятельность по проектированию и реализации образовательного процесса в общеобразовательных организациях (предмет «Математика»)
К этой скидке мы можем добавить скидку для вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курс «Инфоурок»).
В настоящее время в общей сложности 54 252 школы и колледжа имеют право на накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учебного заведения, войдите в личный кабинет Инфоурок.


«Инструменты для формирования умений и навыков самостоятельной работы на уроках математики в 5-9 классах»

1 Слайд Решение задач по «Обобщенной теореме Фалеса».
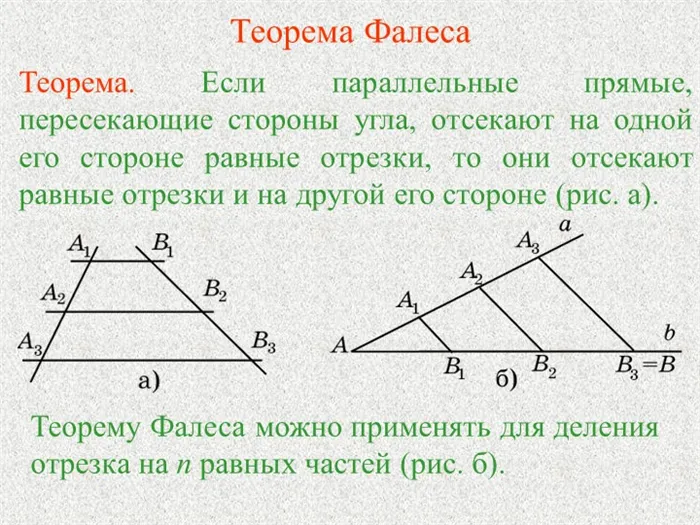
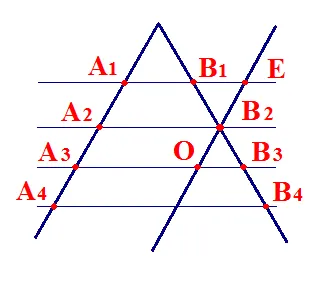
2 Слайд Теорема Фалеса Теорема. Если параллельные прямые, пересекающие стороны угла, пересекают равные отрезки на одной стороне угла, то они также пересекают равные отрезки на другой стороне угла (рис. a). Теорему Фалеса можно применить к делению отрезка на n равных частей (рис. b).

3 слайд Отношение двух отрезков — это отношение их длин, выраженное в одних и тех же единицах. Предложение для пропорциональных отрезков Отрезки AB, CD считаются аналогами A1B1, C1D1, если их отношения AB=1dm CD=5см.

4 Слайд Упражнение 1 Определите, являются ли пары отрезков a, b и c, d аналогами, если: a) a = 0,8 см, b = 0,3 см, c = 2,4 см, d = 0,9 см; b) a = 50 мм, b = 6 см, c = 10 см, d = 18,5 см. Ответ: а) да; б) нет.

5 Слайд Упражнение 2 Выберите пары пропорциональных отрезков среди отрезков a, b, c, d, e, если a = 2 см, b = 17,5 см, c = 16 см, d = 35 см, e = 4 см. Ответ: a, b и e, d.

6 Слайд Задача 3 Даны три отрезка: a, b и c. Какой длины должен быть четвертый отрезок d, чтобы из него можно было составить две пары пропорциональных отрезков, если a = 6 см, b = 3 см, c = 4 см, а отрезок d длиннее каждого из этих отрезков. Ответ: 8 см.
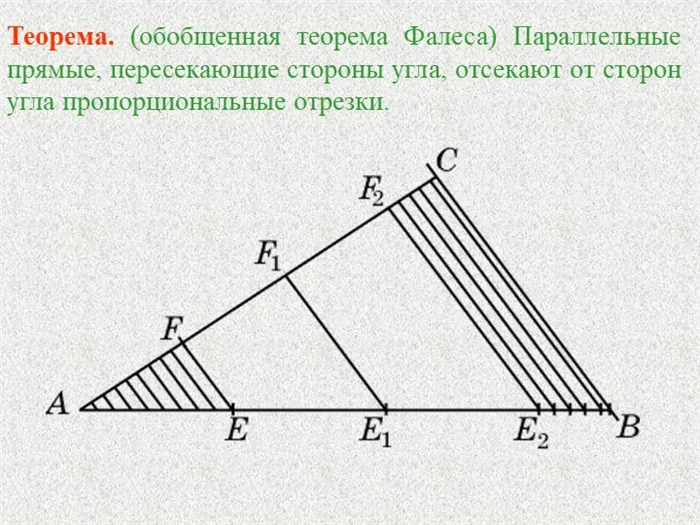
7 Слайды Теорема. (Обобщенная теорема Талеса) Параллельные прямые, рассекающие стороны угла, отсекают пропорциональные отрезки от сторон угла.

8 Слайд Упражнение 4 Стороны угла с вершиной O рассекаются двумя параллельными прямыми в точках A, B и C, D соответственно. Найдите OA, если OB = 15 см и OC : OD = 2 : 5. Ответ: 6 см. OS:OD = 2:5 OA:OB = 2:5
Если на одной из двух прямых последовательно определены равные расстояния и от их концов проведены параллельные прямые до пересечения со второй прямой, то они пересекаются на равных расстояниях на второй прямой.
Более общая формулировка, также называемая теоремой пропорциональности
Параллельные прямые пересекают аналогичные отрезки во вторичные отрезки:
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые A A 1 | | B B 1 | | C C 1 | | D D 1 ||BB_||CC_||DD_>и A B = C D .
Постройте линию BC. Углы ABC и BCD равны как внутренние пересечения при параллелях AB и CD и прямой BC, а углы ACB и CBD равны как внутренние пересечения при параллелях AC и BD и прямой BC. Согласно второму символу равенства треугольников, треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
История
Эта теорема приписывается греческому математику и философу Фалесу Милетскому. Согласно легенде, Фалес Милетский вычислил высоту пирамиды Хуфу, измерив длину своей тени на земле и длину тени палки, измеряющей высоту. Первое известное письменное доказательство этой теоремы содержится в «Началах» Евклида (теорема 2 в книге VI).
Обратная теорема
По теореме Фалеса, если равные части начинаются из вершины (эта формулировка часто используется в школьной литературе), то обратная теорема также верна. Для пересечения вторичных линий она формулируется следующим образом:
Таким образом (см. рис.) из того, что C B 1 C A 1 = B 1 B 2 A 1 A 2 = …>>>=B_>A_>>=ldots>, следует, что A 1 B 1 | | A 2 B 2 | | … B_||A_B_||ldots>.
Если секущие параллельны, то необходимо, чтобы отрезки двух секущих были равны, иначе утверждение ложно (контрпример — трапеция, пересекаемая прямой, проходящей через центры оснований).
Эта теорема используется в навигации: Столкновение судов, движущихся с постоянной скоростью, неизбежно, если направление движения сохраняется от одного судна к другому.
Лемма Соллертинского
Следующее утверждение является дубликатом леммы Соллертинского:
В случае теоремы Фалеса конус — это бесконечно удаленная точка, соответствующая направлению параллельных прямых.
Это утверждение снова является ограничительным случаем следующего утверждения:
- Кто такое Фалес?
- В чем суть теоремы о пропорциональных отрезках?
- Какие отрезки параллельные?
- Программы общеобразовательных учреждений. Геометрия 7-9 классы. Составитель: С.А. Бурмистрова. Москва. «Просвещение», 2009 год.
- П.И. Алтынов, Тесты. Издательский дом «Дрофа».
- Ю. Г. Илларионова. Учите детей отгадывать загадки. Москва «Просвещение»
- А.П. Ершова, В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и геометрии для 7 класса. «ИЛЕКСА». Москва. 2004.
Над курсом работали
На Форуме по образованию, международной встрече для нового мышления и действий в сфере образования, вы можете поднять актуальный вопрос, высказать идею или решить проблему. Создавая блог, вы не только укрепляете свою репутацию компетентного педагога, но и делаете важный вклад в школу будущего. Гильдия лидеров образования открывает свои двери для ведущих профессионалов и приглашает вас к совместной работе по созданию лучших школ в мире.
Подобие в прямоугольном треугольнике
Правильный треугольник характеризуется тем, что его можно легко разделить на два подобных треугольника. Все, что вам нужно сделать, это вставить высоту в гипотенузу:
В самом деле, давайте опустим высоту CH на гипотенузу AB. Пусть ∠A = a в ∆ABC. Вспомните, что сумма острых углов в прямоугольном треугольнике равна 90°. В ∆ABC мы можем написать
Оказывается, что ∆ABC, ∆CN и ∆CN имеют два (и даже три) одинаковых угла и поэтому похожи.
Этот факт также можно использовать для доказательства теоремы Пифагора. Действительно, из подобия ∆АШ и ∆АВС следует, что отношение их гипотенуз равно отношению их перпендикуляров, касательных к углу 90° а:
Аналогично, из подобия ∆CN и ∆ABC следует, что отношение их гипотенуз равно отношению их перпендикуляров, лежащих под углом α:
Преимущество этого доказательства в том, что оно совсем не опирается на понятие площади фигур.
Если мы опустим высоту на гипотенузу, то получим в общей сложности 6 различных отрезков (на рисунке это AB, AC, BC, CH, AH, BH). Если мы знаем длину любых двух из этих отрезков, мы можем найти длину всех остальных.
Задание. В прямоугольнике ∆ ABC высота AH опускается на гипотенузу BC. Известно, что CH = 90, HB = 160. Вычислите все остальные неизвестные отрезки фигуры.

Решение. Самый простой способ найти BC — это сумма CH и HB:
Найдем отрезки AB и AC, применив теорему Пифагора. Сначала напишите его для ∆BH:
Практические задачи
Сходство треугольников также может быть использовано на практике для измерения определенных размеров. Например, давайте измерим высоту одного дерева. Для этого можно просто поместить человека, рост которого, например, известен. Затем нужно измерить длину тени этого человека и самого дерева:
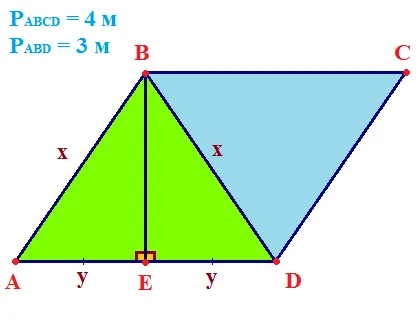
Поскольку тень должна падать под одинаковым углом, можно представить два похожих треугольника:

Предположим, что высота человека составляет 1,8 м, а длина теней от человека и дерева — 1,2 м и 4,8 м. На рисунке ∆ABD и ∆ACE похожи, причем стороны AD и AE одинаковы. Разделите их, чтобы найти коэффициент подобия треугольников:
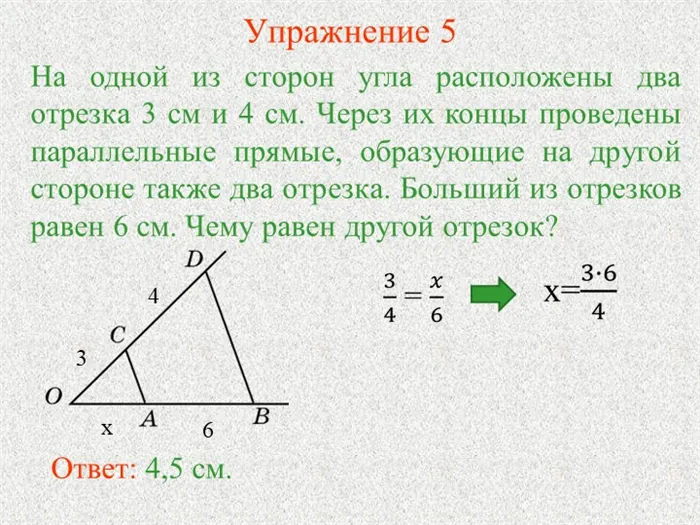
Кроме того, сходство помогает определить расстояние до труднодоступных точек, например, вершин гор. Предположим, что точка B недоступна для нас. Выберите две доступные нам точки A и C и измерьте расстояние между ними. Также измерьте ∠A и ∠C в ∆ABC (используйте прибор, например, астролябию). Затем постройте на бумаге треугольник A1В1С1с теми же углами, но меньшей длины A.1С1:

При черчении можно выбрать определенный масштаб, например, 1:1000. Таким образом, если фактическая длина AB равна 57 м, то на чертеже отрезок A1В1будет в тысячу раз меньше, т.е. 57 мм (1 метр равен ровно 1000 мм). Затем измерьте длину A на чертеже1С1. Пусть оно будет равно 519 мм. Тогда длина фактического измерения AC составит уже 519 метров.
Задачи на построение
Подобие помогает решить некоторые проблемы, связанные с построением фигур. Предположим, нам нужно построить треугольник-k, из которого известны только два угла и длина биссектрисы третьего угла. Решение состоит из 5 шагов:

На первом этапе постройте любой треугольник-c, для которого два угла равны заданным в предпосылке. На втором этапе проведите биссектрису третьего угла полученного треугольника, то есть постройте его биссектрису как радиус, а не как конечный отрезок. На третьем шаге этого радиуса находится отрезок, длина которого соответствует заданной длине биссектрисы угла. Поэтому можно отметить точку на радиусе, которая соответствует концу этого отрезка. На этапе 4 через эту точку проводится прямая, параллельная основанию треугольника. На последнем этапе стороны треугольника продлеваются до пересечения с новой линией. В результате получается новый треугольник, который будет соответствовать условиям задачи.
Аннотация к презентации
Посмотреть и скачать бесплатно презентацию на тему Теорема о пропорциональных пересечениях. состоящую из 28 слайдов. Размер файла составляет 0,76 МБ. Список презентаций, школьных уроков, студенческих и для детей и их родителей.

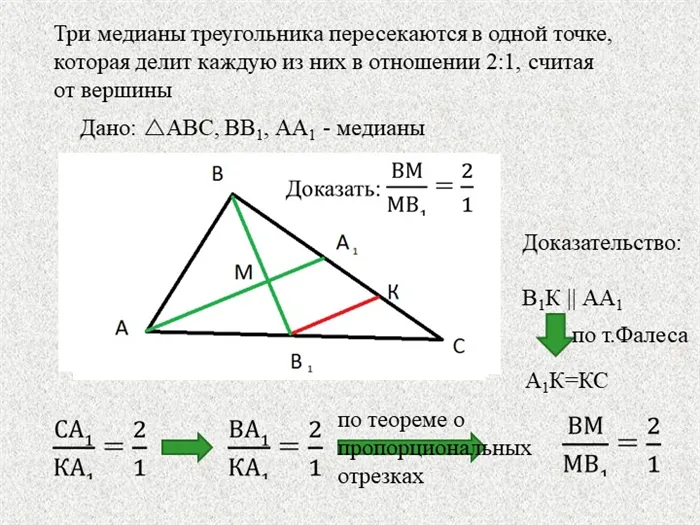
Теорема о пропорциональных отрезках.
Если параллельные прямые пересекают стороны угла, то отрезки, образованные на одной стороне угла, пропорциональны соответствующим отрезкам на другой стороне.

Слайд 2
Итак.Что необходимо?1)Угол.2)Прямые

Слайд 4
И тогда.
Отрезки, образованные на одной стороне угла, пропорциональны соответствующим отрезкам на другой стороне угла.
Слайд 5
Вставьте пропущенные слова.
Если … линии пересекают стороны угла, то отрезки, образованные на одной стороне угла, аналогичны соответствующим отрезкам, образованным на другой стороне угла. Если … линии … стороны угла, то отрезки, образованные на одной стороне угла, пропорциональны соответствующим отрезкам, образованным на другой стороне угла.
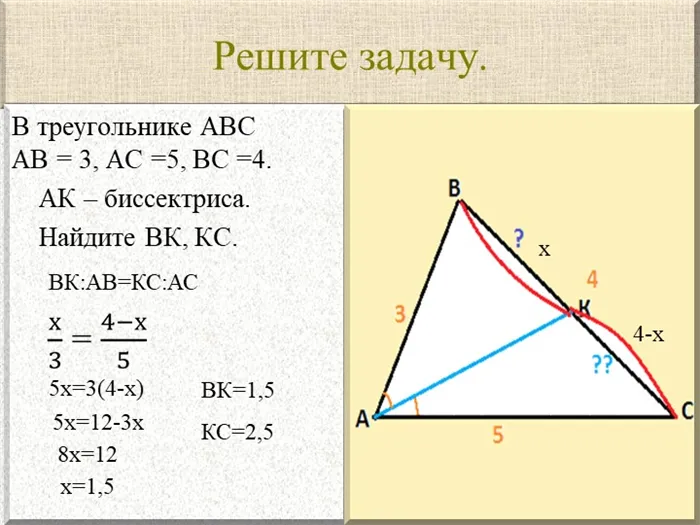
Слайд 6 Если параллельные прямые пересекают стороны угла, то образуют …. на одной стороне угла, … соответствующие отрезки на другой стороне угла. Если параллельные прямые пересекают стороны угла, то отрезки … на одной стороне угла аналогичны соответствующим …. на другой стороне угла образуются … .

Слайд 7
Верно ли
Если перпендикулярные прямые пересекают стороны угла, то отрезки, образованные на одной стороне угла, пропорциональны соответствующим отрезкам, образованным на другой стороне угла. Если параллельные прямые пересекают стороны угла, то отрезки, образованные на одной стороне угла, равны соответствующим отрезкам, образованным на другой стороне угла.

Слайд 8
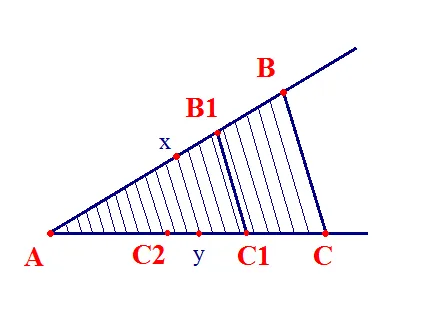
На рисунке АВ=4, СD =6,ЕF=3, КL=8

Слайд 9 Решите задачуНа рисунке BD|| SE, AB=16см, BC=6см, AD=8см. Найдите отрезок DE.
Решите следующие номера.

Слайд 11
На каком рисунке изображена медиана?
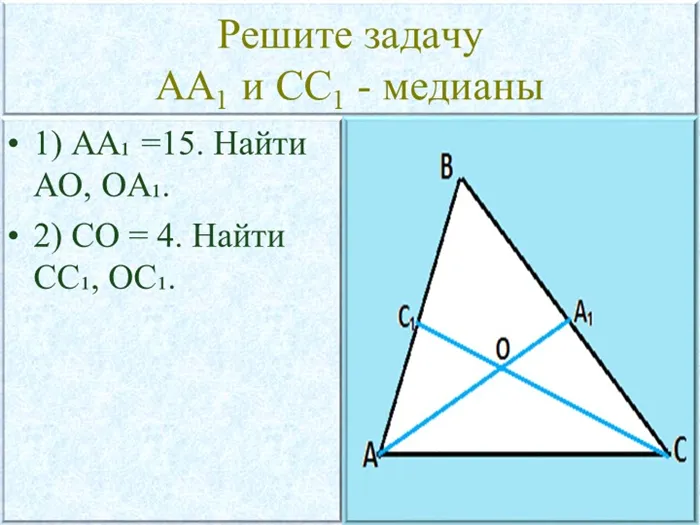
Слайд 12
Давайте вспомним, что же называется медианой?
Определение: Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
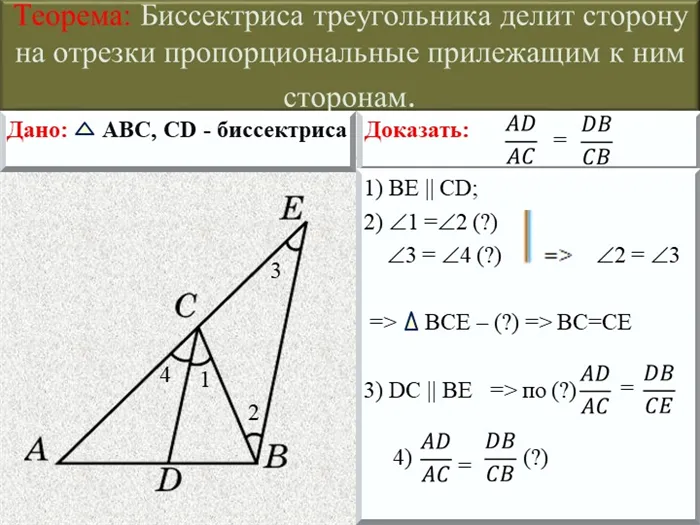
Слайд 13








