Теорема — это предложение, в котором условие является заключением данного предложения, а заключение — условием данного предложения Метод опровержения Метод предположения противоположности того, что должно быть доказано.
Параллельные прямые: свойства и признаки
Параллельные линии — В планетометрии линии, которые не пересекаются, независимо от того, сколько их в любом направлении. В стереометрии две прямые считаются параллельными, если они лежат в одной плоскости и не пересекаются.
- В случае, если две прямые параллельны третьей, они являются параллельными между собой. Так, если а || c и также b || c, то и a || b.
- Если они перпендикулярны по отношению к третьей, то они не пересекаются: т.е., если а ⊥ с и b ⊥ c, то a || b.

Свойства параллельных прямых с доказательством
Свойства параллельных прямых — это утверждения, которые являются обратными по отношению к ранее упомянутым пунктам.
Осторожно. Если преподаватель обнаружит плагиат в вашей работе, вы можете избежать больших неприятностей (вплоть до исключения из университета). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Вы обладаете следующими характеристиками:

- Через любую точку, которая, что немаловажно, не лежит на прямой, можно провести параллель, притом лишь одну. Данное утверждение является Евклидовой аксиомой .
- Если прямая, лежащая на плоскости, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой: если a || b и c ⊥ a, то c ⊥ b.
Дано: a || b и c ⊥ a
- с пересекает а, следовательно, с пересекает также прямую, параллельную а, т.е. b.
- Исходя из этого, можно утверждать, что с — это секущая по отношению к а и b.
- При секущей с ∠1 и ∠2 являются накрест лежащими.
- Из свойств углов при параллельных прямых, пересеченных секущей, нам известно о равенстве накрест лежащих углов: следовательно, ∠1 = ∠2.
- Как следствие, ∠2 = 90 градусов, что означает, что c ⊥ b. Что и требовалось доказать.
Признаки при пересечении секущей
Минор — это линия, которая пересекает линию:
- кривую в двух точках;
- или две прямые, которые лежат в этой же плоскости, в двух разных точках.
Рассмотрим точки, отмечающие параллельные прямые, когда их пересекает второстепенная прямая.
Если соответствующие углы равны, то линии не пересекаются. Если ∠2 = ∠4, то a || b.
Если сумма односторонних внутренних углов равна 180 градусам, то прямые параллельны. Если ∠1 + ∠2 = 180°, то a || b.

Если внутренние углы пересечения равны, то прямые также параллельны. Если ∠1 = ∠3, то a || b.

Свойства параллельных прямых

Свойства параллельных прямых очень часто используются при решении задач и доказательстве теорем. Произвольные прямые встречаются редко, но есть фигуры, такие как квадрат или параллелограмм, где параллельные прямые могут лечь в основу задачи, и без знания свойств параллельных прямых невозможно решить такие задачи.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Что такое свойства параллельных прямых
Сначала мы объясним определения, необходимые для изучения свойств параллельных прямых.
Параллельные прямые — это прямые, не имеющие общих точек, или прямые, которые не пересекаются и лежат в одной плоскости.
Пересечение означает, что два объекта имеют общую точку или множество точек. Поэтому, когда геометрия говорит, что линии имеют общую точку, это означает, что они пересекаются.
Когда две прямые пересекаются вторичной прямой, образуются углы пересечения, соответствующие углы и диагональные углы.
Для параллельных прямых существует аксиома, которая очень важна для доказательства некоторых свойств и является фундаментальным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости может проходить только прямая, параллельная определенной прямой.
Две группы свойств параллельных прямых
Существует 5 свойств параллельных прямых, но они делятся на две большие группы: Следствия из аксиомы параллельных прямых и следствия из параллельных точек прямых. Давайте начнем с первой группы.
Следствия из аксиомы параллельных прямых
Следствие 1
Если одна из двух параллельных прямых параллельна третьей, то другая прямая также параллельна ей.
Это кажется логичным и не требует доказательств. В геометрии, однако, число утверждений, не требующих доказательства, чрезвычайно мало, и каждое из них называется аксиомой.
Аксиомы восходят к истокам геометрии и с тех пор практически не изменились. Большинство современных теорем вытекают из аксиом Древней Греции. Эти утверждения — единственные в математике, которые не нуждаются в доказательстве.
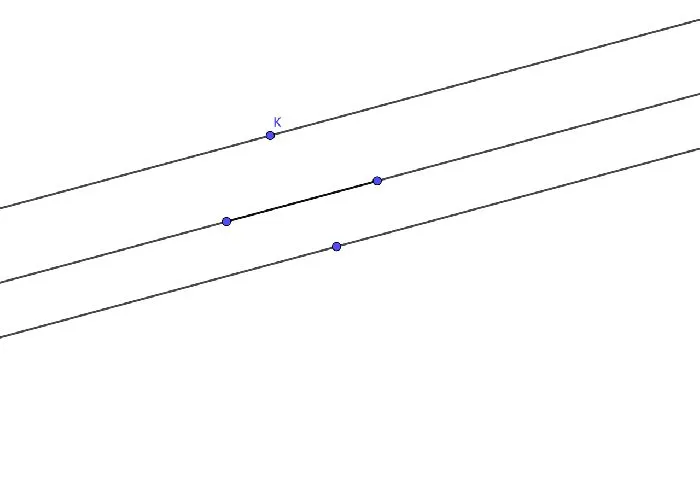
Начертите две параллельные прямые a и b. Прямая c параллельна прямой a. Предположим, что c не параллельна прямой b. Поэтому через точку K проходят две прямые c и b. Каждая из этих прямых должна быть параллельна прямой a.
То есть две прямые, параллельные данной прямой, проходят через одну и ту же точку плоскости. Это невозможно, так как противоречит аксиоме о параллельных прямых. Следовательно, первоначальное предположение было неверным, и c и b параллельны.
Следствие 2
Вывод 2 очень важен, потому что он говорит нам о вторичности двух параллельных прямых. Свойство гласит, что прямая, пересекающая одну из параллельных прямых, пересекает и другую прямую.
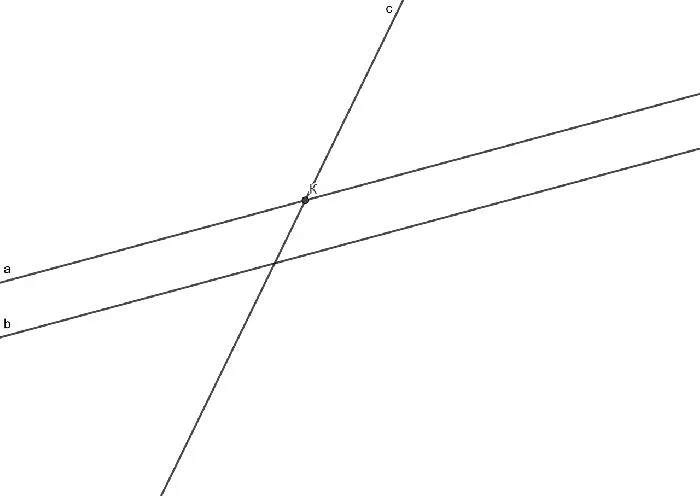
Доказательство можно провести и в обратном направлении. Введем две прямые: a и b. Предположим, что прямая c пересекает a, но не пересекает b. Тогда c и b параллельны. Следовательно, c пересекает a; эти две прямые имеют общую точку K.
Тогда прямые a и c проходят через точку K, но обе параллельны b. Следовательно, две прямые, параллельные прямой b, проходят через одну и ту же точку, что невозможно согласно аксиоме о параллельных прямых. Следовательно, исходное утверждение было ложным, а линия c пересекает каждую из линий a и b, что и требуется доказать.
Следствия из признаков параллельности
Эту группу легче всего запомнить. Существует 3 свойства параллельных прямых, и каждое из них имеет свои последствия.
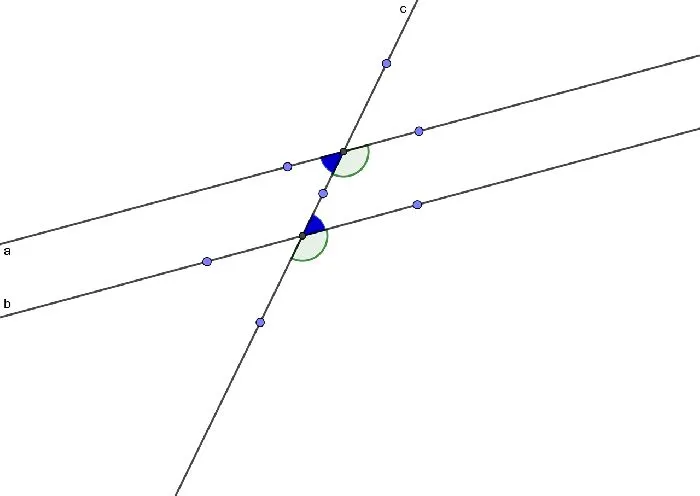
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
Свойства параллельных прямых – основные определения
Свойства параллельных прямых очень часто используются при решении задач и доказательстве теорем. Произвольные прямые встречаются редко, но есть фигуры, такие как квадрат или параллелограмм, где параллельные прямые могут лечь в основу задачи, и без знания свойств параллельных прямых невозможно решить такие задачи.

Что такое свойства параллельных прямых
Сначала мы объясним определения, необходимые для изучения свойств параллельных прямых.
Параллельные прямые — это прямые, не имеющие общих точек, или прямые, которые не пересекаются.
Пересечение означает, что два объекта имеют общую точку или множество точек. Поэтому, когда геометрия говорит, что линии имеют общую точку, это означает, что они пересекаются.
Когда две прямые пересекаются вторичной прямой, образуются углы пересечения, соответствующие углы и диагональные углы.
Для параллельных прямых существует аксиома, которая очень важна для доказательства некоторых свойств и является фундаментальным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости может проходить только прямая, параллельная определенной прямой.
Две группы свойств параллельных прямых
Существует 5 свойств параллельных прямых, но они делятся на две большие группы: Следствия из аксиомы параллельных прямых и следствия из параллельных точек прямых. Давайте начнем с первой группы.
Следствия из параллельности прямых
Следствие 1
Если одна из двух параллельных прямых параллельна третьей, то другая прямая также параллельна ей.
Это кажется логичным и не требует доказательств. Но в геометрии число утверждений, не требующих доказательства, чрезвычайно мало, и каждое из них называется аксиомой.
Аксиомы восходят к истокам геометрии и с тех пор практически не изменились. Большинство современных теорем вытекают из аксиом Древней Греции. Эти утверждения — единственные в математике, которые не нуждаются в доказательстве.
Начертите две параллельные прямые a и b. Прямая c параллельна прямой a. Предположим, что c не параллельна прямой b. Поэтому через точку K проходят две прямые c и b. Каждая из этих прямых должна быть параллельна прямой a.
То есть две прямые, параллельные данной прямой, проходят через одну и ту же точку плоскости. Это невозможно, так как противоречит аксиоме о параллельных прямых. Следовательно, первоначальное предположение было неверным, и c и b параллельны.
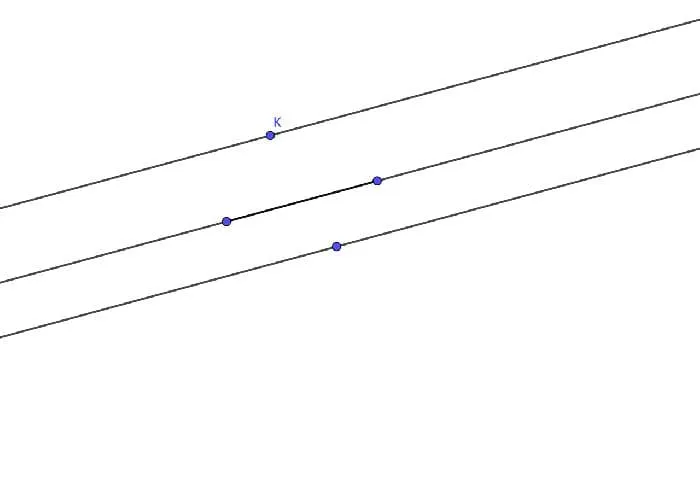
Рисунок 1. Иллюстрация последовательности.
Следствие 2
Вывод 2 очень важен, потому что он говорит нам о вторичности двух параллельных прямых. Свойство гласит, что прямая, пересекающая одну из параллельных прямых, пересекает и другую прямую.
Доказательство можно провести и в обратном направлении. Введем две прямые: a и b. Предположим, что прямая c пересекает a, но не пересекает b. Тогда c и b параллельны. Следовательно, c пересекает a; эти две прямые имеют общую точку K.
Тогда прямые a и c проходят через точку K, но обе параллельны b. Следовательно, две прямые, параллельные прямой b, проходят через одну и ту же точку, что невозможно согласно аксиоме о параллельных прямых. Значит, первоначальная гипотеза была неверной, и линия c пересекает каждую из линий a и b, что и требовалось доказать.
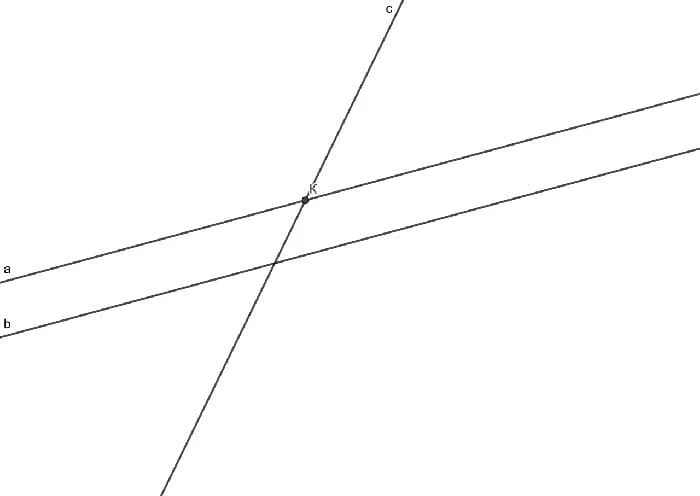
Рисунок 2. Номер для доказательства.
Следствия из признаков параллельности
Эту группу легче всего запомнить. Существует 3 свойства параллельных прямых, и каждое из них имеет свои последствия.
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
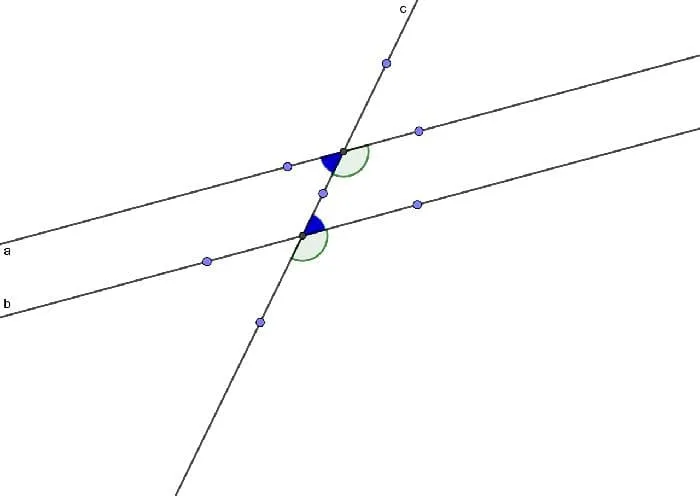
Рисунок 3. Иллюстрация доказательства.








