Для получения абсолютного (положительного эквивалентного) значения данного целого числа работает следующее, потому что знак » — » меняет значение с отрицательного на положительное (оно отрицательное, потому что «x» возвращает true).
Алгебра логики
Логическая алгебра — это раздел математики, в котором рассматриваются логические значения высказываний (истина или ложь) и логические операции над этими высказываниями. Иногда ее называют двоичной логикой или алгеброй Буля, в честь английского математика Джорджа Буля.
Для простоты они используют обозначение F для результата и A ( X ) и B ( Y ) для логических утверждений. Поскольку существует только два возможных значения, их можно обозначить 0 (ложь, нет, ложь, нет) и 1 (правда, да, правда, да).
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные комбинации истинностных значений входных сигналов (операторов) вместе с истинностным значением выходного сигнала (результата операции) для каждой из этих комбинаций.
Логическое высказывание
Логическое высказывание — это повествовательное предложение, для которого мы можем однозначно сказать, истинно оно или ложно.
Тождественно истинные высказывания (тавтология)
Высказывание считается тождественно истинным, если оно истинно для всех значений составляющих его переменных.
Поэтому такое утверждение всегда равно 1.
Высказывание — это, например, уточнение термина на основе его словообразования (an air base is an air base) или составное высказывание, смысл которого сводится к формуле A \/ ¬A.
Тождественно ложные высказывания
Идентично ложные утверждения — это утверждения, которые ложны для всех значений переменных, из которых они состоят.
Следовательно, это утверждение всегда равно 0.
Важно отметить, что большинство утверждений сводится к формуле A /\ ¬A.
Эквивалентные высказывания
Эквивалентные (одинаковые или эквивалентные) высказывания — это высказывания, значения которых совпадают для любых значений их переменных.
Логические операции
- логическое умножение (конъюнкция или логическое И) AND, &, /\;
- логическое сложение (дизъюнкция или логическое ИЛИ) OR, |, \/;
- логическое отрицание (инверсия или логическое НЕ) NOT, ¬, ;
- логическое следование (импликация) →;
- логическое равенство (эквивалентность) ↔, ~.
Логическое умножение (конъюнкция)
Это соединение нескольких логических выражений с помощью операции AND. В практическом компьютерном вводе символы прямого и обратного деления часто используются без пробелов.
Таким образом, все значения должны быть истинными: И первое, И второе, И. При умножении логических операторов мы получим единицу только если все они будут равны единице:
| A | B | F = A И B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
В результате получается обратная последовательность, которая упрощает вычисления для конъюнкции: если хотя бы одно значение ложно, то все выражение ложно.
Логическое сложение (дизъюнкция)
Представляет собой объединение логических выражений с помощью союза ИЛИ. Если при сложении результат становится больше нуля, то он выражается единицей. При практическом наборе на компьютере часто используют знаки обратного и прямого деления без пробела: \/
| A | B | F = A \/ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Поэтому обратная последовательность упрощает вычисления для дизъюнкции: если хотя бы одно значение истинно, то истинно и все выражение.
Логическое отрицание (инверсия)
Представляет собой логическое выражение с добавленной в начале частицей НЕ. То есть операция всегда обращает значение в противоположное.
| A | F = ¬ A |
| 0 | 1 |
| 1 | 0 |
Логическое следование (импликация)
Связывает два логических выражения с помощью оборота ЕСЛИ. ТО. Дополнительная операция, так как A → B = \/ B Кроме того, при построении высказывания могут использоваться выражения «из. следует», «. влечет».
| A | B | F = A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблица хорошо иллюстрирует практический аспект: заключение ложно только в том случае, если первое выражение истинно, а второе ложно.
При решении задач применение закона устранения импликации необходимо в большинстве случаев.
Логическое равенство (эквивалентность)
Образуется соединением двух логических выражений с помощью оборотов «тогда и только тогда», «необходимо и достаточно», «. равносильно. ». Поскольку мы видим здесь двойное следование (и вправо и влево), операцию иногда называют двойной импликацией. Дополнительная операция, так как A ↔ B = ( A ∨ ) & ( ∨ B )
| A | B | F = A ↔ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Нет согласия относительно того, можно ли определить отрицание с точки зрения его логического статуса, его функции и значения, сферы применения и интерпретации отрицательного суждения (FH Heinemann 1944).
Классическое отрицание — это операция над одним логическим значением, обычно значением предложения, которая производит значение val ue ue, которое имеет значение true, если его оператор ложен, и значение false, если его оператор истинен. Таким образом, если выражение P истинно, то ¬ P (произносится «не P») ложно; и наоборот, если ¬ P ложно, то P истинно.
| P | ¬ P |
| Правда | Ложь |
| Ложь | Правда |
Отрицание может быть определено в терминах других логических действий. Например, ¬ P можно определить как P → ⊥ (где → — логическое следствие, а ⊥ — абсолютная ложь). И наоборот, ⊥ можно определить как Q ∧ ¬ Q для любого предложения Q (где ∧ — логическая связка). Идея здесь заключается в том, что каждое противоречие ложно, и хотя эти идеи работают как в классической, так и в интуиционистской логике, они не работают в параконтрастивной логике, где противоречия не обязательно ложны. В классической логике существует дополнительное тождество: P → Q можно определить как ¬ P ∨ Q, где ∨ — логическая дизъюнкция.
Алгебраически классическое отрицание соответствует комплементу в булевой алгебре, а интуиционистское отрицание — псевдокомплементу в алгебре Гейтинга. Эти алгебры обеспечивают семантику для классической и интуиционистской логики соответственно.
Обозначение
Отрицание предложения p символизируется по-разному в различных контекстах обсуждения и применения. В таблице ниже описаны некоторые из этих вариантов:
В теории множеств ∖ также используется для обозначения «нечлена множества»: U ∖ A — это множество всех членов U, которые не являются членами A .
Отрицание ¬ P, независимо от того, как оно сформулировано или символизировано, может быть прочитано как «это не случай P», «не то, что P», или обычно более просто как «не P».
Свойства
Двойное отрицание
В системе классической логики двойное отрицание, т.е. отрицание отрицания отрицания отрицания отрицания отрицания отрицания отрицания отрицания предложения P, логически эквивалентно P. Это выражается в символических терминах: ¬ ¬ P ≡ P. В интуиционистской логике предложение влечет за собой двойное отрицание, но не наоборот. В этом заключается важное различие между классическим и интуиционистским отрицанием. Алгебраически классическое отрицание называется складыванием периодов.
Однако в интуиционистской логике эквивалентность ¬ ¬ P ≡ ¬ P не выполняется. Более того, предложение классически доказуемо, если его двойное отрицание интуитивно доказуемо. Этот результат известен как теорема Гливенко.
Распределительность
Линейность
Пусть ⊕ — логическая операция xor. В булевой алгебре линейная функция — это функция, которая выглядит следующим образом:
Если существует a 0, a 1,…, an ∈, a_, \ dots, a_ \ in \>, f (b 1, b 2,…, bn) = a 0 ⊕ (a 1 ∧ b 1) ⊕ ⊕ (an ∧ bn)<\ displaystyle f (b_, b_, \ dots, b_ ) = a_ \ oplus (a_ \ land b_ ) \ oplus \ dots \ oplus (a_ \ land b_ )>, для всех b 1, b 2,…, bn ∈<\ displaystyle b_, b_, \ dots, b_ \ in \>.
Другой способ выразить это состоит в том, что каждая переменная всегда имеет истинностное значение — значение действия, иначе она бессмысленна. Отрицание — это линейный логический оператор.
Самодвойственная
В булевой алгебре автоморфная функция — это функция, для которой выполняется::
f (a 1,…, an) = ¬ f ( ¬ a 1,…, ¬ an), \ dots, a_ ) = \ neg f (\ neg a_, \ dots, \ neg a_ )>для всех a 1,…, an ∈ .<\ displaystyle a_, \ dots, a_ \ in \>. Отрицание — это самодвоичный логический оператор.
Отрицание кванторов
В логике первого порядка есть два квантора: универсальный квантор ∀ (означает «для всех») и экзистенциальный квантор ∃ (означает «есть»). Отрицанием одного квантификатора является другой квантификатор ( ¬ ∀ x P (x) ≡ ∃ x ¬ P (x) и ¬ ∃ x P (x) ≡ ∀ x ¬ P (x) ). С предикатом P как «x смертен» и областью x как множеством всех людей, ∀ x P (x) означает, например, «человек x из всех людей смертен» или «все люди смертны». Его отрицание: ¬ ∀ x P (x) ≡ ∃ x ¬ P (x), что означает «среди всех людей есть человек x, который не смертен», или «есть тот, кто живет вечно».
Инверсия (отрицание)
Операция логической инверсии — это единичная операция над высказываниями, с помощью которой высказывание преобразуется в противоположное исходному высказыванию.
Другие названия отрицания — отрицание или логическое НЕТ.
Инверсия или отрицание изучается в информатике в разделе алгебры логической алгебры.
В естественных языках отрицание соответствует частице «не» или словам «ложно, что». Например, если высказывание A = «Москва является столицей России», то его отрицание будет «Москва не является столицей России».
В языках программирования используется обозначение ‘ not ‘ или восклицательный знак ‘ ! ‘ (например, not(x = 5) или !<3) ).
Для обозначения отрицания используется символ отрицания ¬ или тире над утверждением. Например, отрицание A может быть обозначено либо ¬A, либо \overline.
Как набрать знак инверсии на клавиатуре
Чтобы ввести символ ¬ в Word, удерживая левую клавишу Alt на цифровой клавиатуре (в правой части клавиатуры), введите 0172, т.е. символ ¬ — это Alt+0172. Функция Num Lock должна быть активирована.
Чтобы сделать черту над буквой, необходимо зайти в пункт меню Вставка ->Формула (или уравнение). Затем найдите отличительные символы на панели инструментов и между ними нужный символ с дефисом над буквой.
Пример
Даны два отрезка B = 2,10, C = 6,14. Выберите отрезок A, для которого формула \( ((z \в A) \Longrightarrow (z \в B)) \vee (z \in C)\) для каждого значения z. Варианты ответов:
Решение: подставим \( ((z \в A) \Longrightarrow (z \в B)) в уравнение. \вее (z \в C) \) = 1, и сформировать таблицу истинности:
Полученная формула \( ((z \in A) \Longrightarrow (z \in 2,10)) \вее (z \в 6,14)=1 \). По условию, \( z \ в A \)=1.
Таблица истинности для всех сегментов:
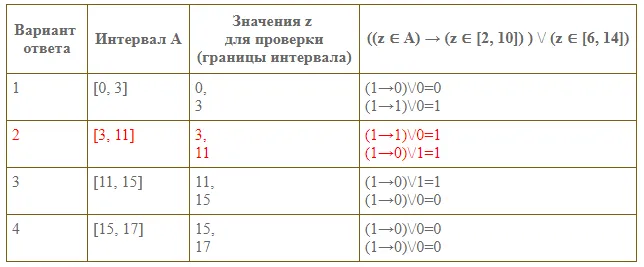
Ответ.








