Дисъюнкция — это логическая операция, объединяющая два предложения в новое предложение, которое истинно, если истинно хотя бы одно из исходных предложений. Дисъюнкция также является двойной операцией, т.е. она должна содержать две логические переменные.
Логические основы ЭВМ
Каждый цифровой компьютер состоит из логических схем, то есть схем, которые могут принимать только одно из двух возможных состояний — либо «логический ноль», либо «логическая единица». Каждое выражение может быть интерпретировано как логический 0 и логическая 1, а также может быть описано как «истинно» и «ложно». В компьютерной технологии логические 0 и логические 1 — это состояния электрических цепей с определенными параметрами. В транзисторно-транзисторных логических схемах, например, логический 0 — это напряжение в диапазоне 0 … + 0,4 В, тогда как логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В 1. + 5 В 1. Функционирование логических схем описывается с помощью специальной математической процедуры, называемой логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864) и является основой для всех методов упрощения булевых выражений.
Логические переменные и логические функции — это переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическую 1.
Основные логические функции и элементы
Логический элемент — это графическое представление элементарной логической функции.
Рассмотрим ключевую схему, показанную на рисунке 1.1,a. Примем логический 0 за логическую 2:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
- на выходе схемы ( не протекает .
Таблица истинности — это таблица, содержащая все возможные комбинации логических входных переменных и соответствующих значений логической функции.
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — и =8″ />. Очевидно, что ток течет через резистор R только тогда, когда все три клавиши замкнуты — и, и
Правило логического умножения: Если к входу логического элемента И подключен хотя бы один логический 0, то на выходе получается логический 0.
Уровень логического 0 является определяющим для логического умножения.
В логических выражениях используется несколько вариантов нотации логического умножения. Например, для элемента AND с тремя входами, показанного на рисунке 1.1.c, логическое выражение может быть представлено следующим образом:

- либо
- либо ;
- либо
- либо, производится логическое умножение.
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим схему ключа, показанную на рисунке 1.2,a. Таблица истинности для этой логической схемы (рис. 1.2,b) состоит из 4 строк, поскольку эта схема имеет два входа -. Очевидно, что через резистор R протекает ток, когда замыкается либо логическое ИЛИ, либо логическое ИЛИ. В логических схемах соответствующий логический элемент, независимо от элементной базы, на которой он реализован, характеризуется, как показано на рис. 1.2.c.
Правило логического сложения: Если на вход элемента логического ИЛИ подается хотя бы один элемент логического ИЛИ, то определителем является количество элементов ИЛИ на входе элемента логического ИЛИ.
В логическом сложении уровень логической 1 является определяющим.
Существует два способа задания логического дополнения в логических выражениях. Таким образом, логическое выражение для данного элемента ИЛИ с двумя входами может быть представлено следующим образом:
-
либо
либо
Логическая операция ИЛИ (OR)
Операция логического ИЛИ выполняется с двумя битами (a и b). Результат операции логического ИЛИ равен 0, если a и b равны 0 (нулю), а во всех остальных случаях результат равен 1 (единице). См. таблицу истинности для операции логического ИЛИ.
| a (бит 1) | b (бит 2) | a(бит 1) | b(бит 2) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логическая операция исключающее ИЛИ (XOR).
Нотация XOR: ^ Операция логического ИЛИ выполняется с двумя битами (a и b). Результат операции XOR равен 1 (единице), если один из битов a или b равен 1 (единице), в противном случае он равен 0 (нулю). См. таблицу истинности операции логического ИЛИ.
| a (бит 1) | b (бит 2) | a(бит 1) ^ b(бит 2) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логическая операция НЕ (not)
Условные обозначения НЕ: ~ Логическая операция НЕ выполняется с одним битом. Результат этой логической операции напрямую зависит от состояния бита. Если бы бит находился в состоянии ноль, результатом NOT была бы единица, и наоборот. См. таблицу истинности для логической операции НЕ.
| a (бит 1) | ~a (отрицание битов) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Запомните эти 4 логические операции. С помощью этих логических операций мы можем получить любой возможный результат. Подробнее об использовании логических операций в C++ читайте здесь.
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС
К этой скидке мы можем добавить скидку вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы «Инфоурок»).
В настоящее время 54 334 учебных заведения имеют право на накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Infourock.
Курс переподготовки
Разработка и сопровождение требований и технических заданий на разработку и модернизацию систем и подсистем малого и среднего масштаба и сложности
К этой скидке мы можем добавить скидку вашего учебного заведения (в зависимости от того, сколько ваших коллег прошли курсы «Инфоурок»).
В настоящее время 54 334 учебных заведения имеют право на накопительные скидки (от 2% до 25%). Чтобы узнать, какая скидка распространяется на всех сотрудников вашего учреждения, войдите в личный кабинет Infourock.


«Основы работы с программой PowerPoint»
Тема: «Логические операции «И», «Или», «Нет». КР1″ Цели урока: Формирование: получить представление о простейших логических операциях; Развитие: развивать логическое мышление, познавательный интерес; Формирование: демонстрировать наглядность, слуховое восприятие, коммуникативную культуру. Курс урока. 1. утверждения — домашняя работа домашнее задание контрольная работа контрольная работа — вопросы Каковы объекты алгебры? (Заявления)Что такое заявление? Все ли утверждения являются утверждениями? Приведите 4 примера утверждений. Приведите 4 примера не утверждений. В каком смысле рассматриваются утверждения? (С точки зрения истинности или ложности) 2. Объяснение по новой теме. Логические выражения могут быть простыми и сложными. Простое логическое выражение состоит из одного оператора и не содержит логических операций. Простое логическое выражение может иметь только два исхода — либо «истина», либо «ложь». Сложное логическое выражение содержит утверждения, объединенные логическими операциями. В сложных логических выражениях используются логические операции. Существует три основных операции над высказываниями: логическое сложение, логическое умножение и отрицание. Операция NOT применяется к аргументу, который может быть простым или сложным утверждением. Результатом операции NOT является «false», если исходное выражение истинно, и «true», если исходное выражение ложно. Для операции отрицания используются следующие термины: НЕ A,┐A,, не A. Таблица, содержащая все возможные значения исходных выражений и соответствующие результаты операции, называется таблицей истинности. A 0 1 1 1 1 0 Задание 1. Создайте отрицание для логического выражения. Найдите результат операции отрицания. Земля вращается вокруг Солнца. Пушкин — гениальный русский поэт. 5x = 10.4 — простое число. OR — логическое сложение (деление, соединение) Логическая операция OR имеет функцию объединения двух высказываний, которые могут быть как простым, так и сложным логическим выражением. Типичные обозначения: A или B, A \/B, A + B, A или B. Результатом операции OR является выражение, которое истинно только в том случае, если истинно хотя бы одно или оба исходных выражения. A B A\/B 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Задание 2. Составьте дизъюнкцию логических выражений. Марина больше, чем Света. Оля выше Лилии. В кабинете есть учебники. В офисе есть несколько справочников. Некоторые туристы любят чай. Другие туристы предпочитают молоко. Синий кубик меньше красного. Синий кубик меньше зеленого. AND — логическое умножение (конъюнкция) Логическая операция AND имеет функцию пересечения двух высказываний, которые могут быть простыми или сложными логическими выражениями. Примечания: А и В, А / В, А ∙ В, А и В. Результатом операции AND является выражение, которое истинно, если оба утверждения истинны. A B A/\B 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 1 Задача 3. Составьте объединение логических выражений.
Специальное предложение до 30 ноября
- Опытные онлайн-репетиторы
- Подготовка к ЕГЭ и ОГЭ
- По всем школьным предметам 1-11 класс

Логическое НЕ !
! (восклицательный знак) — это единичный оператор, который предшествует оператору и устанавливает аргумент в логическое значение true или false, а затем возвращает противоположное значение.
console.log( !true ); // false console.log( !false ); // true console.log( !'text' ); // false console.log( !5 ); // false console.log( !0 ); // trueВ свою очередь, двойное отрицание !!! используется для преобразования значения в логический тип.
console.log( !!true ); // true console.log( !!false ); // false console.log( !!text' ); // true console.log( !!5 ); // true console.log( !!0 ); // falseЭквивалентом этой конструкции является встроенная булева функция
console.log( Boolean('text') ); // true console.log( Boolean(5) ); // true console.log( Boolean(0) ); // trueЛогически, ! имеет более высокий приоритет, чем || и &&, поэтому, если вы хотите отменить выражение, заключите его в круглые скобки.
console.log( !(true && false) ); // true console.log( !true && false ); // false console.log( !(true || true) ); // false console.log( !true || true); // true console.log( !true || true ); // trueИтого
В этом уроке мы подробно рассмотрели логические операторы:
- && (и) — возвращает true, когда оба операнда true, в противном случае false ;
- || (или) — возвращает false, если два операнда false, во всех остальных случаях true ;
- ! (не) — возвращает true, если значение операнда false и наоборот;
Из этих трех операторов наивысший приоритет выполнения имеет оператор ! (не), затем && (и), и только затем || (или).
Логические величины, операции и выражения
Во время изучения информатики студенты уже познакомились с логическими множествами, выражениями и операциями. На этом уроке они смогут вспомнить, что такое логические величины, и проанализировать логические операции, такие как конъюнкция, дизъюнкция и инверсия. Они также узнают о новой логической операции — исключающем ИЛИ. В этом видео рассматриваются операции с логическими выражениями. При написании сложного логического выражения (предиката) необходимо учитывать приоритеты арифметических, логических и реляционных операций. Все эти правила описаны в данном уроке.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам, необходимо добавить их в свой личный шкафчик.

2. распространить видеоуроки в ваших личных кабинетах среди ваших учеников.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Логические величины, операции и выражения»
В этом уроке мы вспомним, что такое логические величины, и обсудим логические операции, такие как конъюнкция, дизъюнкция и инверсия. Мы также будем работать с логическими выражениями.
В курсе информатики вы уже имели дело с логическими множествами, выражениями и операциями. Давайте вспомним, что такое выражение. Выражение — это повествовательное предложение на любом языке, в котором что-то утверждается или отрицается. То есть, любое выражение можно определить как истинное или ложное.
Рассмотрим следующие предложения:
— Клавиатура используется для ввода текстовой информации и команд для управления компьютером.
— Получение информации — это процесс передачи информации от источника к получателю.
Эти предложения относятся к высказываниям, потому что мы можем с уверенностью сказать, истинны они или ложны. Первое утверждение истинно, второе — ложно.
А вот следующие заявления:
— Не поднимайте трубку!
Они не являются утверждениями, потому что, по определению, утверждение — это повествовательное предложение.
Для построения высказываний можно использовать символы из различных формальных языков: Математика, физика, химия и другие.
Числовые выражения не являются выражениями. Если мы построим выражение из двух выражений и соединим их символом равенства или неравенства, то новое выражение будет выражением.

Логические предложения могут быть простыми и сложными.
Простое высказывание — это такое высказывание, в котором ни одна часть не является высказыванием сама по себе.
Сложное или составное высказывание — это высказывание, состоящее из простых высказываний с использованием логических операций.
Логические значения — это понятия, выражаемые словами true или false. Истинность высказывания выражается логическими значениями.
Логическая переменная — это символически объявленное логическое значение. Это означает, что логическая переменная может быть обозначена, например, буквой римского алфавита. Сама буква является переменной логического значения. Он может принимать только значение True или False.
Логическое выражение — это простое или сложное высказывание. Составное высказывание, как мы уже знаем, строится из простых высказываний с помощью логических операций (конъюнкции).
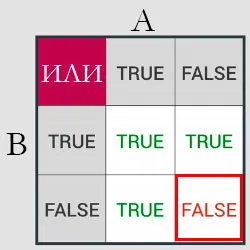
Булевы операции — это конъюнкция, дизъюнкция и инверсия (отрицание). Давайте рассмотрим отдельные логические операции.
Поэтому первой логической операцией является сопряжение — логическое умножение.
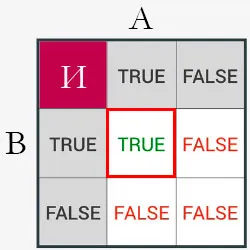
Конъюнкция — это логическая операция, объединяющая два предложения в новое предложение, которое является ложным, если хотя бы одно из исходных предложений ложно. Спряжение — это двойная операция, что означает, что она должна содержать две логические переменные.
В естественном языке конъюнкция эквивалентна конъюнкции «И». В алгебре конъюнкция может быть представлена различными символами: символ точки «&», символ конъюнкции «/\» и символ умножения «-«. В языках программирования конъюнкция обозначается английским «AND», символом точки «&» или двоеточием «&&».








