Теорема Пусть две точки A(x1; y1; z1) и B(x2; y2; z2), координаты вектора \( \вертикальная стрелка \) определяются по следующим формулам:
Калькулятор онлайн. Длина вектора. Модуль вектора.
Этот электронный калькулятор вычисляет длину (модуль) вектора. Вектор может быть определен в 2- или 3-мерном пространстве.
Калькулятор модуля не только отвечает на задачу, но и предоставляет подробное решение с пояснениями, т.е. показывает процедуру решения, чтобы проверить ваши навыки математики и/или алгебры.
Этот электронный калькулятор может пригодиться школьникам при подготовке к экзаменам и тестам, в качестве проверки знаний перед государственными экзаменами, а также родителям для проверки решения многих задач по математике и алгебре. Или вам слишком дорого нанимать репетитора или покупать новые книги? А может быть, вы просто хотите как можно быстрее выполнить домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробными решениями.
Таким образом, вы сможете научить себя и/или научить своих младших братьев и сестер и повысить уровень обучения решению проблем.
Если вы не знакомы с правилами ввода чисел, мы рекомендуем вам ознакомиться с ними.
Числа могут быть представлены как целые числа или как дроби. Доли можно вводить как дроби или как десятичные дроби.
Чтобы ввести десятичную дробь, введите ее как дробь. В десятичных дробях дробь может быть отделена от целого числа полной остановкой или запятой. Например, десятичную дробь можно ввести как 2,5 или 1,3.
Правила импорта фракций. Только целые числители, знаменатели и целые части дроби могут быть целыми числами.
Знаменатель не может быть отрицательным числом.
При вставке дроби числитель отделяется от знаменателя знаком деления: / Вставить: -2/3 Результат: \( -\frac \).
Целая часть отделяется от дробной символом точки: & Вставка: -1&5/7 Результат: \( -1\frac \).
Вычисление длины (модуля) вектора
Было обнаружено, что некоторые скрипты, необходимые для решения этой проблемы, не были загружены, поэтому программа может не работать. Возможно, у вас включен AdBlock. Если да, отключите его и обновите страницу.
Поскольку так много людей заинтересованы в решении этой проблемы, ваш запрос был добавлен в очередь. Через несколько секунд решение будет показано ниже. Пожалуйста, подождите немного.
Игра «droneZone» —>3D модели Создание острова Эмулятор гравитации Игра «iChart» —>Головоломка SumWaves
Немного теории.
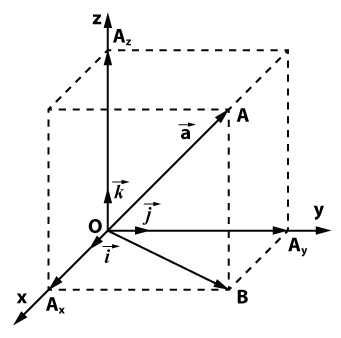
Многие физические величины полностью определяются конкретным числом. Например: объем, масса, плотность, температура тела и т.д. Эти величины называются скалярными величинами. По этой причине числа иногда называют скалярными величинами. Однако существуют и такие величины, которые определяются не только числом, но и определенным направлением. Например, если тело движется, необходимо указать не только скорость, с которой оно движется, но и направление движения. Кроме того, при изучении действия какой-либо силы необходимо определить не только величину этой силы, но и направление ее действия. Эти величины называются векторными величинами. Для их описания было введено понятие вектора, которое оказалось полезным в математике.
Каждая упорядоченная пара точек A — B в пространстве определяет направленный отрезок, то есть отрезок вместе с заданным им направлением. Если A — первая точка, то она называется началом направленного отрезка, а B — концом направленного отрезка. Направление отрезка — это направление от начала к концу.
Определение Направленный отрезок называется вектором.
Обозначим вектор через \( \overrightarrow \), где первая буква обозначает начало вектора, а вторая — конец вектора.
Вектор, который имеет одинаковое начало и конец, называется нулевым и обозначается \( \vec \) или просто 0.
Расстояние между началом и концом вектора называется длиной и обозначается \( |\overrightarrow| \) или \( |\vec| \).
Нулевой вектор предполагается прямолинейным, как и любой другой вектор; его длина равна нулю, т.е. \( |\vec| = 0 \).
Теперь мы можем сформулировать важную концепцию равенства двух векторов.

Определение Векторы \( \vec||) и \( \vec||) равны (\( \vec|| = \vec||)), если они коллинеарны, выпрямлены и их длины равны.
Проекция вектора на ось
Пусть в пространстве есть ось \( u \) и вектор \( \overrightarrow \). Проведите плоскости, перпендикулярные оси \( u \) через точки A и B. Обозначим через A’ и B’ точки пересечения этих плоскостей с осью (см. рисунок 2).
Проекция вектора \( \overrightarrow \) на ось \( u \) — это значение A’B’ направленного отрезка A’B’ на оси \( u \). Напомним, что \( A’B’ = |\overrightarrow| \) если направление \( \overrightarrow| \) совпадает с направлением оси \( u \), \( A’B’ = -\\\\overrightarrow| \) если направление \( \overrightarrow| \) противоположно направлению оси \( u \). Проекция вектора \( \overrightarrow| \) на ось \( u \) называется \( Pr_u \overrightarrow| \).
Теорема Проекция вектора \( \overrightarrow \) на ось \( u \) равна длине вектора \( \overrightarrow \), умноженной на косинус угла между вектором \( \overrightarrow \) и осью \( u \), т.е. \( Pr_u \overrightarrow = |\overrightarrow||\cos \varphi \), где \( \varphi \) — угол между вектором \( \overrightarrow \) и осью \( u \).
Применение формулы теоремы к каждому из этих векторов дает \( Pr_u \overrightarrow = Pr_u \overrightarrow \), т.е. равные векторы имеют равные проекции на одну и ту же ось.
Калькулятор для вычисления длины вектора (модуля вектора) по двум точкам
Инструкция использования калькулятора для вычисления длины вектора
- выберите из выпадающего списка необходимую вам размерность и форму представления вектора;
- введите значение вектора;
- Нажмите кнопку «Найти длину вектора» и вы получите детальное решение задачи.
Ввод данных в калькулятор для вычисления длины вектора (модуля вектора)
В электронный калькулятор можно вводить числа или дроби. Для получения дополнительной информации см. правила ввода цифр.
Дополнительные возможности калькулятора для вычисления длины вектора (модуля вектора)
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Нахождение длины вектора
Формула для определения длины вектора \(\vec a\) зависит от его положения. Если она лежит в плоскости, т.е. \(\vec a=\left(a_x;a_y
ight)\), то для его вычисления необходима формула:
Внимание! Если профессор обнаружит плагиат в вашей работе, у вас будут большие неприятности (вплоть до исключения). Если вы не можете написать работу самостоятельно, закажите ее здесь.
Найдите длину вектора \(\vec a\) с координатами (5; -3).
Исходные данные \(a_x=5,\) \(a_y=-3\) подставьте в формулу и вычислите.
Если вектор находится в пространственной системе, т.е. \(\vec a=\left(a_x;a_y;a_z
ight),\) тогда нам нужна формула для расчета:
Длина вектора через координаты точек его начала и конца
Найдите длину вектора \(\vec a\) с координатами (2; 2; 2; 4).
Вставьте координаты из штата и рассчитайте:
В предыдущем разделе мы определили длину вектора с помощью координат. Однако, если они неизвестны, длину можно рассчитать, используя координаты начальной и конечной точек.
Если даны две точки: \(A\links(a_x;a_y
ight) и B\links(b_x;b_y
ight),\) тогда вектор \(\vec AB\) имеет координаты \(\links(b_x-a_x;b_y-a_y
Нахождение длины вектора по теореме косинусов
ight).\)
Отсюда формула:
Найдите длину вектора \(\vec AB\), если A (1; 3), B (3; 6).
Формула для трехмерного пространства выглядит следующим образом:
Найдите длину вектора \(\vec AB\), если A (0; 1; 3), B (2; 3; 6).
Однако из-за этой проблемы координаты вектора не всегда известны. Тогда мы должны искать другие возможные решения.
Например, мы знаем длины двух векторов \(\vec AB\) и \(\vec AC\) и угол между ними. Нам нужно найти вектор \(\vec BC\). В этом случае мы можем обратиться к теореме косинусов для определения значения вектора.
Теорема косинусов гласит, что квадрат одной стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
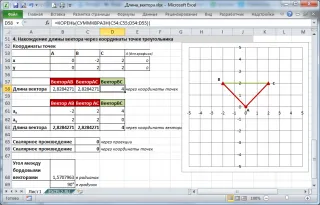
Нахождение длины вектора через координаты точек треугольника
Длина вектора \(\vec AB=2\), \(\vec AC=4\), а угол между ними \(=\frac\pi4.\).
Вычислите длину вектора \(\vec BC.\).
Длина вектора \(\vec BC\) равна длине стороны BC треугольника ΔABC.
Сложение векторов
Исходные данные позволяют применить теорему косинусов, так как длины сторон треугольника известны (они равны длинам векторов \(\vec AB\) и \(\vec AC\)) и угол между ними также известен.
\(BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos\angle\left(\vec AB,\vec AC
ight)=2^2+4^2-2\cdot2\cdot4\cdot\cos\frac\pi4=4+16-8\sqrt2=20-8\sqrt2\)
Предположим, что мы получили 3 точки треугольника, образованного векторами.
Найдите длину вектора BC по координатам соответствующих точек (как во 2-й задаче, рассмотренной выше) по формуле =RANE(C54:C55;D54:D55) .
Если вы знаете координаты точек, вы можете определить все длины сторон (длины векторов) и углы треугольника (используя теорему косинусов).
Существует два способа сложения векторов.








