Обратные функции

Содержание

Если у нас есть числовое множество X и правило f, которое позволяет нам присвоить определенное число y каждому элементу x множества X, то мы говорим, что у нас есть функция y = f ( x ) с областью X.

Обратная функция презентация к уроку по алгебре (10 класс) на тему

Снова Если каждому значению x из множества действительных чисел соответствует число y по правилу f, то мы говорим, что существует функция, определенная на этом множестве. D(f ) — область функции; x — независимая переменная или аргумент; y — зависимая переменная; множество всех значений y=f(x), x ϵ X называется областью функции и обозначается E(f ).

Задача Дана функция y=f(x) Найти значение функции при х=х 0 Например: найти значение функции y=5x+7 в точке х=7. y(7)=5∙7+7 Ответ: y(7)=42 =35+7=42 Задача на прямую Дана функция y=f(x) Найти значение аргумента в точке у=у 0 Например: Дана функция y=5x+7. Найти значение аргумента, где у=22. 22=5x+7 5x=22-7 5 x=15 x=15:5 x =3 Ответ.

Задача Пусть требуется найти закон изменения скорости движения от времени Найти закон изменения времени от скорости. Решение.

Если функция принимает любое значение y при значении x, то говорят, что функция инвертируема. Предположим, что функция инвертируема. Тогда для каждого набора значений функции существует определенное число в области, такое, что это соответствие определяет функцию, которую мы обозначим через. Давайте обменяемся и : Функция называется обратной функцией функции. Он обозначается.

Пример Найти обратную функцию Решение: Ответ:

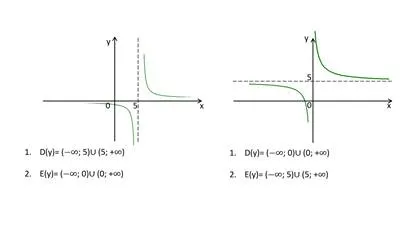
y x 5 0 D(y)= ( ; ; 5) E(y )= ( ; 0) y 0 5 x D(y)= ( ; 0) E(y )= ( ; 5)

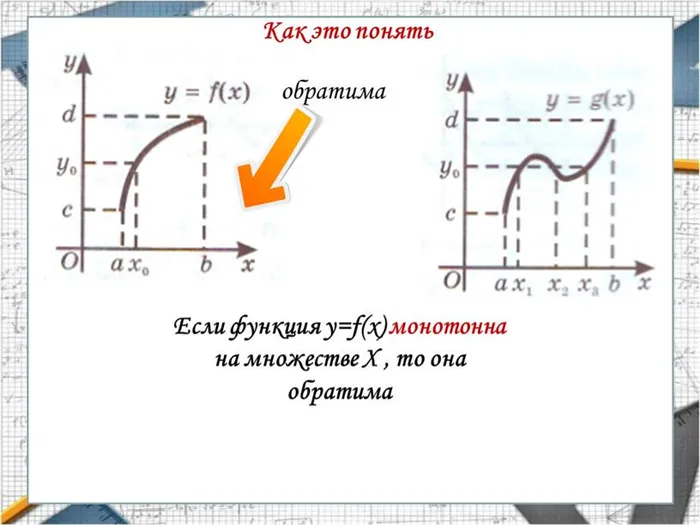
Свойства обратных функций: Область определения обратной функции совпадает с множеством значений выходной функции, а множество значений обратной функции совпадает с областью определения выходной функции Монотонная функция является обратимой: а) если функция возрастает, то обратная ей функция также возрастает; б) если функция убывает, то обратная ей функция также убывает.

Пример Покажите, что для функции существует обратная функция, и найдите ее аналитическое выражение. Решение: Функция возрастает в R. Тогда обратная функция существует в R. Решите уравнение в терминах. Получите, Подставьте и получите : Это и есть искомая обратная функция.

Пример На функции Докажите, что существует обратная функция, запишите аналитическое выражение обратной функции в виде и постройте график обратной функции.

Решение: Поскольку функция возрастает на интервале, она имеет обратную функцию. Из уравнения получаем: или. Только значения функции принадлежат интервалу .

Подставляя и, график этой функции получается из графика функции с симметрией относительно прямой.

По теме: методические разработки, презентации и конспекты

Открытый курс по теме «Функция: понятие, методы определения и основные характеристики. Обратная функция. Суперпозиция функций».

В нем содержатся основные характеристики функции. Даны определения обратной и сложной функций.

Математическая лаборатория «Обратная функция

Материал может быть использован для подготовки к уроку.

2 Презентации учащихся по теме «Обратные функции».

Понятие обратной функции, ее свойства и примеры.

Обратные обратные функции

Презентация по теме «Обратные функции», подведение итогов и тест для проверки знаний учащихся.

Открытый урок по теме «Обратная функция» (2019).

Разработка открытого урока по математике в 10 классе.

Обратная функция

Конспект по теме: «Обратная функция».

Презентация к уроку алгебры в 10 классе. Включает самостоятельную работу.

Обратные функции – определение и свойства

Определение обратной функции и ее свойств: теорема о взаимной монотонности прямой и обратной функций; симметрия графиков прямой и обратной функций; теоремы о существовании и непрерывности обратной функции для строго монотонной функции на отрезке, интервале и полуинтервале. Примеры обратных функций. Пример решения проблемы.

Предположим, что функция имеет область X и область Y. Пусть она обладает свойством: для всех. Тогда для каждого элемента из множества Y можно назначить только один элемент из множества X, для которого. Это соответствие определяет функцию, называемую обратной функцией от. Обратная функция обозначается через .

Из определения следует, что ; для всех, для всех .

Теорема существования и монотонности для обратной функции Если функция f строго возрастает (убывает), то существует обратная функция, которая также строго возрастает (убывает). Доказательство

Свойство симметрии графиков прямых и обратных функций Пусть f ( x ) — функция f ( x ), определенная на множестве X и множестве значений Y : f ( X ) ∈ Y. Пусть f-1 : f-1 ( Y ) ∈ X имеет обратную функцию f ∈ Y. Тогда графики прямой и обратной функций f-1 симметричны относительно прямых линий для аргументов x ∈ X и x ∈ Y, соответственно. Доказательство

Теорема о существовании и непрерывности обратной функции на отрезке Пусть функция непрерывна и строго возрастает (строго убывает) на отрезке. Тогда обратная функция, которая строго возрастает (строго убывает), определена и непрерывна на отрезке. Для возрастающей функции. Для убывающей функции:. Доказательство

Теорема о существовании и непрерывности обратной функции на интервале Пусть функция непрерывна и строго возрастает (строго убывает) на открытом конечном или бесконечном интервале. Тогда обратная функция, которая строго возрастает (строго убывает), определена и непрерывна на интервале. Для возрастающей функции. Для убывающей функции:. Доказательство

Теорема о существовании и непрерывности обратной функции в полупространстве Если функция непрерывна и строго монотонна в полупространстве X, то в полупространстве Y обратная функция определена и строго монотонна и непрерывна. Если она строго возрастает, то она также строго возрастает. Поэтому: если, то ; если, то. Если она строго убывающая, то она также строго убывающая. Поэтому: если, то ; если, то. Вот. Открытым краем интервала может быть конечное число или бесконечно удаленная точка. Доказательство

Примеры обратных функций

Арксинус

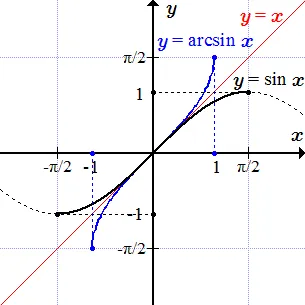
Рассмотрим тригонометрическую функцию синус: она определенна и непрерывна для всех значений аргумента, но она не монотонна. Однако, если ограничить область определения, можно выделить монотонные части. Таким образом, на отрезке функция является определенной, непрерывной, строго возрастающей и принимает значения о т-1 до +1. Поэтому она содержит обратную функцию, так называемый дуговой синус. Синус дуги имеет поле определения и свой набор значений.

Логарифм

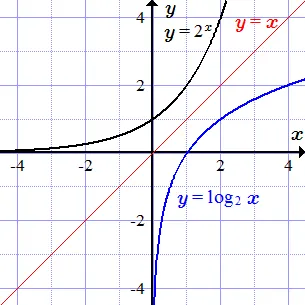
Функция экспоненты единственна, непрерывна и строго возрастает при всех значениях члена. Диапазон его значений — это открытый интервал. Обратной функцией является логарифм по основанию два. Он имеет область определения и свой набор значений.

Квадратный корень

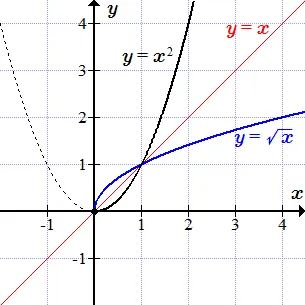
Функция мощности является определенной и непрерывной для всех. Множество его значений является полуинтервалом из. Однако он не является монотонным для всех значений аргумента. В полуинтервале, однако, она непрерывна и строго монотонно возрастает. Таким образом, если множество, то существует обратная функция, квадратный корень. Обратная функция имеет область определения и множество значений .

Пример. Доказательство существования и единственности корня степени n

Все примеры Докажите, что уравнение, где n — натуральное число, — действительное неотрицательное число, имеет единственное решение в множестве действительных чисел,. Это решение называется корнем степени n из числа a. То есть, мы должны показать, что каждое неотрицательное число имеет единственный корень степени n.

Рассмотрим функцию на переменной x : (P1) .

Мы хотим доказать, что она непрерывна. Используя определение непрерывности, мы покажем, что биномиальная формула Ньютона имеет место: (P2). Применим числовые свойства пределов функций. Поскольку только первый член отличен от нуля:. Непрерывность доказана.

Докажем, что (P1) строго возрастает в. Возьмем произвольные числа, связанные неравенствами:, , ,. Мы должны показать, что. Введем переменные. Затем Поскольку (P2) показывает, что. или. Мы доказываем строгое дополнение.

Мы ищем множество значений функции при. В точке, находим предел. Для этого применим неравенство Бернулли. Дано. Применяя свойство неравенств бесконечных функций, находим, что, так как, и .

Согласно теореме об обратной функции, обратная функция определена и непрерывна на интервале. Поскольку мы имеем, это означает, что для любого, уравнение имеет единственное решение — корень степени n из числа x: .

Использованная литература. Москва, 2004 г. С.М. Никольский. М.С. Николай, М.С. Сокольский. С.С. Николай. Москва, 1983.

Автор.

Области определения и множества значений двух различных функций одинаковы, но одна из функций обратимая (т

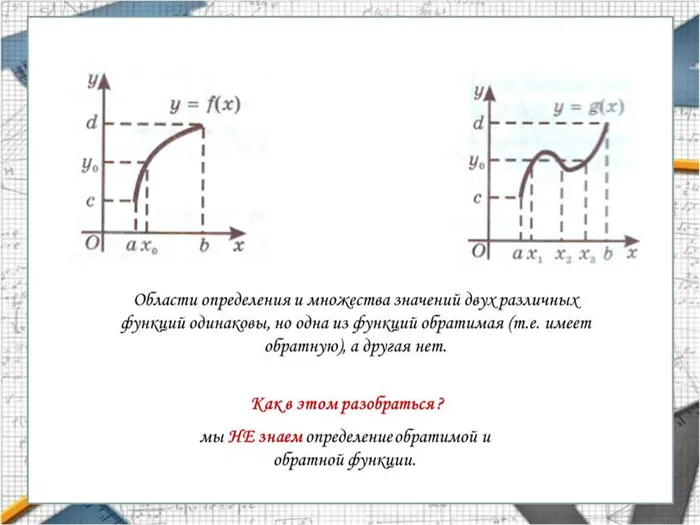
Поля определения и наборы значений двух различных функций одинаковы, но одна из функций инвертируема (т.е. имеет обратную величину), а другая — нет.

Мы НЕ знаем определения инвертируемой и обратной функции.

Как мы можем это понять?

Что такое обратная функция? Как найти функцию, обратную данной?

Что такое обратная функция? Как найти обратную функцию?Определение.

Пусть функция y=f(x) определена на множестве D и пусть E — множество ее значений. Обратная функция y=f(x) — это функция x=g(y), определенная на множестве E, которая присваивает каждому y∈E такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью определения обратной функции этой функции, а область определения y=f(x) является областью определения обратной функции этой функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо : 1)

Чтобы найти обратную функцию y=f(x), необходимо:

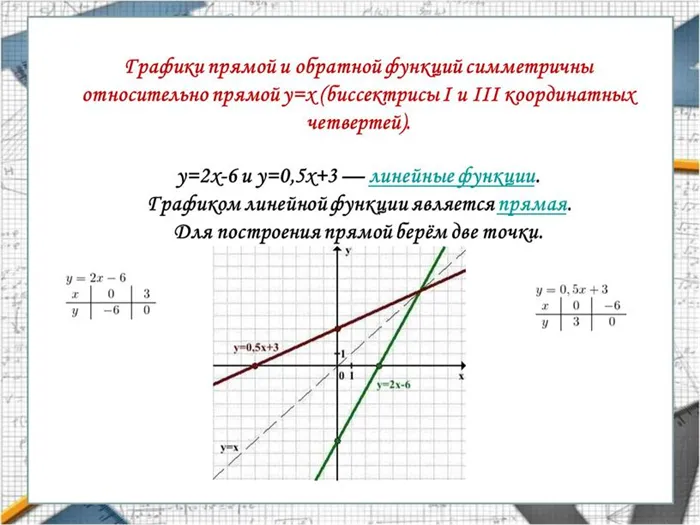
1) Подставьте x вместо y в формулу функции и замените x на y: x=f(y). 2) Выразите y через x из полученного уравнения: y=g(x).

Пример. Найдите обратную функцию y=2x-6. 1) x=2y-6 2) -2y=-x-6 y=0,5x+3.

Функции y=2x-6 и y=0,5x+3 являются обратными друг другу.

Свойства взаимно обратных функций

1) Личности. Пусть f и g — обратные функции друг к другу. Это означает, что уравнения y = f(x) и x=g(y) эквивалентны. Подставьте одно из этих уравнений в другое. У нас есть две личности:

Примеры:

Пусть f — показательная, g — логарифмическая функция. Получаем знакомые тождества:

2. функции y = являются обратными друг другу. У нас есть две личности:

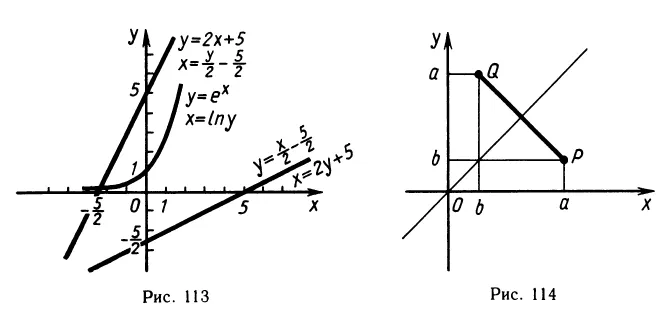
2) Область определения. Пусть f и g — взаимнооднозначные функции. Область функции f совпадает с областью функции g, и наоборот, область функции f совпадает с областью функции g. Фактически, обратная функция y = f(x) определена для любого числа y, которое является значением функции f для числа x: мы получаем равенство y = f(x) и отсюда можем выразить l: как функцию от y. Это свойство хорошо видно на графике: график функции y = f(x) совпадает с графиком обратной функции x = g(y), за исключением того, что аргумент функции g лежит на оси y. Понятно, что аргументами функции g являются значения функции f и наоборот.

Пример. Область определения экспоненциальной функции — вся числовая ось R, а область ее значений — множество всех положительных чисел. Для логарифмической функции все наоборот: ее область определения — множество всех положительных чисел, а область значений — все множество R.

Теорема:

Если одна из взаимно обратных функций строго возрастает, то другая функция также строго возрастает.

Если только f и g не являются взаимно обратными функциями и f строго возрастает. Докажите, что тогда g также строго возрастает. Пусть x₁и х₂— два числа в области определения функции g и x₁2. Мы должны доказать, что g ( x₁)x₂Обозначим через g(x1) = y1, g( x₂)=y2. Мы должны доказать, что g(x)x₁) = yi, g( x₂) = y2. Числа y1 и y2 лежат в области определения функции f, поскольку они являются значениями функции g. Предположим, что y1 ≥ y2. В силу монотонности f мы имеем f<у1) ≥<у2). Но f (y1) = f1)) = x₁и f (y2)= x₂То есть, x₁≥ x₂что противоречит условию x₁2. Следовательно, y1

Мы выводим общую формулу для производной обратной функции так же, как выводили формулу для производной логарифмической функции. Пусть f и g — обратные функции друг к другу. Как найти производную функции g, если известна производная функции f?

Графики функций y = f(x) и y = g(x) симметричны относительно биссектрисы I угла xOu (рис. 116,a).

Возьмите любую точку x = a и вычислите значение одной из функций в этой точке: f (a)=b. Согласно определению обратной функции g (b)-a.

Точки (a;f (a)) = (a; b) и (b; g (b))=(b; a) симметричны относительно данной прямой l. Поскольку кривые симметричны, касательные к ним также симметричны относительно прямой l.