Нежное введение в линейную алгебру. Что такое линейная алгебра.

Обычно студенты, изучающие статистику, рассчитывают пройти по крайней мере один семестр линейной алгебры (или прикладной алгебры) во время обучения в бакалавриате.

Линейная алгебра в переводе на нормальный язык

Хотя я прослушал два курса линейной алгебры, все мои знания о неи состояли из «таблиц, определителей, всего, что подходит».

Почему так происходит? Давайте уточним специфику моего курса:

• Название курса «Линейная алгебра», но почему-то упор делается на термины вроде матриц и векторов
• Суть обучения сводилась к порядку строк/колонок с мнемоникой вместо пояснения самого смысла происходящего
• Предпочтение отдавалось абстрактным примерам (2-мерные векторы! 3-мерные векторы!), и до самой последней недели мы всячески избегали примеров из реального мира

В такой битве между терминологией и смыслом выживают только физики, графические программисты и прочие мазохисты. Мы потеряли самое необходимое:

Линейная алгебра дает вам мини-таблицы для математических уравнений.

Вы можете взять таблицу данных (электронную таблицу) и создать на ее основе обновленные таблицы. В этом и заключается сила расчетной таблицы, записанной в виде уравнения.

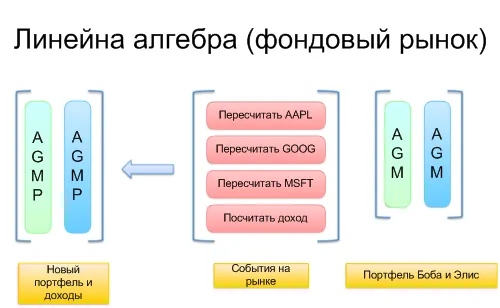
Мне бы очень пригодилось такое введение в линейную алгебру в моем курсе, с объяснением на реальном примере с фондового рынка.

Что в имени тебе моем?

«Алгебра» приблизительно означает «связи». Алгебра в начальной школе показывает связи между неизвестными числами. Не зная x и y, можно утверждать, что (x + y) 2 = x 2 + 2xy + y 2

«Линейная алгебра» в общем смысле означает «линейно-подобные соединения». Здесь мы остановимся на деталях.

Прямые линии предсказуемы. Представьте, что вы идете по крыше: вы поднимаетесь на 3 метра вверх по склону и оказываетесь ровно в 1 метре над землей (вы идете по склону! уклон / пройденное расстояние = 1/3). Если вы пройдете 6 метров, вы уже находитесь на высоте 2 метров над землей. Сравните подъем на крышу с подъемом на купол: с каждым метром, пройденным по горизонтали, вы достигаете разной высоты над землей.

Линии очень красивые и предсказуемые:

• Если 3 метра вперед подымают на 1 метр, тогда пройденный путь длиной в 10х раз больше должен поднять вас над землей на 10х высоту (30 метров пути дают 10-метровый подъем)
• Если 3 метра, пройденных по крыше, подымают человека на 1 метр над землей, а 6 метров пути дают подъем на 2 метра, тогда (3 + 6) метров пути должны подымать на (1 + 2) метра

Математически операция F является линейной, если масштабирование исходных параметров масштабирует их значение:

В нашем примере F(x) рассчитывает подъем, когда мы поднимаемся по скату крыши на x метров, и эти пропорции сохраняются:

Линейные операции

Функция — это вычисление на основе определенных входных параметров. Какие функции являются линейными и предсказуемыми? Операция умножения кажется хорошим примером.

Экспоненты (F(x)=x 2 ) не предсказуемы: 10 2 равно 100, а 20 2 равно 400. Мы удвоили входной параметр, но умножили результат.

Это вас удивит, но даже обычное сложение не является линейным. Рассмотрим функцию плюс 3:

Мы удвоили аргумент (входное значение), а не результат. (Да, функция F(x) = x + 3 является уравнением прямой линии, но она все еще не является «линейной», потому что F(10) не равно 10*F(1). Смешно).

Наша единственная надежда — умножение на константу: F(x) = ax (в нашем примере с крышей a=1/3). Тем не менее, мы можем комбинировать линейные операции для создания новой линейной операции:

G состоит из 3 линейных частей: Если мы удвоили аргументы, то мы удвоили значение самой функции.

Здесь мы используем «мини-арифметику»: умножаем аргументы на константу и складываем результаты. Это довольно полезная техника, поскольку она позволяет нам разделить аргументы, проанализировать их по отдельности, а затем суммировать результаты:

Если бы аргументы вели себя как экспоненты, их нельзя было бы разделить — здесь нужно анализировать все сразу, а не по отдельности.

Линейная алгебра — это раздел математики, но на самом деле линейная алгебра — это математика данных. Таблицы и векторы — это язык данных.

Линейная алгебра для линейных комбинаций. То есть, использование арифметики для столбцов чисел, называемых векторами, и столбцов чисел, называемых таблицами, для создания новых столбцов чисел и столбцов чисел. Линейная алгебра — это изучение прямых и плоскостей, векторных пространств и отображений, необходимых для линейных преобразований.

Это относительно новая область исследования, впервые формализованная в 1800-х годах для нахождения неизвестных в системах линейных уравнений. Линейное уравнение — это просто последовательность терминов и математических операций, где некоторые термины неизвестны, например:

Эти уравнения являются линейными в том смысле, что они описывают линию на двумерном графике. Линия получается путем подстановки различных значений для неизвестного x, чтобы определить, что уравнение или модель делает со значением y. Уравнение или модель может быть системой уравнений.

Например, мы можем построить систему уравнений одного типа с двумя или более неизвестными:

y = 0,1 * x1 + 0,4 * x2 y = 0,3 * x1 + 0,9 * x2 y = 0,2 * x1 + 0,3 * x2 .

Столбец значений y можно рассматривать как вектор столбца исходного уравнения. Два столбца со значениями с плавающей точкой являются столбцами данных, например, a1 и a2, и могут рассматриваться как матрица A. Два неизвестных значения x1 и x2 могут рассматриваться как коэффициенты уравнения и вместе образуют вектор неизвестных b. Мы можем записать уравнение компактно с помощью линейной алгебраической нотации следующим образом:

Задачи такого типа обычно трудно решить, потому что неизвестных (здесь 2) больше, чем уравнений, которые нужно решить (здесь 3). Более того, часто не существует прямой линии, которая безошибочно удовлетворяла бы всем уравнениям. Системы, описывающие часто интересующие нас проблемы (например, линейная регрессия), могут иметь бесконечное число решений.

Это дает небольшое представление о природе линейной алгебры, которая интересует нас как практиков машинного обучения. Большая часть остальной функции направлена на то, чтобы облегчить понимание и решение этой проблемы и аналогичных проблем.

Численная линейная алгебра

Компьютерные приложения линейной алгебры часто называют численной линейной алгеброй.

«Численная» линейная алгебра на самом деле является приложением линейной алгебры.

Она включает в себя не только реализацию операций линейной алгебры в библиотеках кода, но и тщательное решение проблем прикладной математики, например, решение проблемы ограниченной точности вычислений с плавающей запятой в цифровых компьютерах.

Компьютеры хорошо справляются с вычислениями в линейной алгебре, и во многом использование графических процессоров (GPU) в современных методах машинного обучения, таких как Deep Learning, связано с их способностью быстро вычислять операции линейной алгебры.

Эффективные реализации векторных и матричных операций были первоначально реализованы на языке программирования FORTRAN в 1970-х и 1980-х годах, и большая часть кода или кода, перенесенного из этих реализаций, составляет основу большей части линейной алгебры, выполняемой с помощью современных языков программирования, таких как Python.

Три популярные библиотеки численной линейной алгебры с открытым исходным кодом реализуют эти функции:

• Пакет линейной алгебры или LAPACK.
• Основные подпрограммы линейной алгебры, или BLAS (стандарт для библиотек линейной алгебры).
• Автоматически настраиваемое программное обеспечение линейной алгебры, или ATLAS.

Если вы вычисляете операции линейной алгебры прямо или косвенно с помощью алгоритмов более высокого порядка, ваш код, вероятно, использует одну из этих или подобных библиотек линейной алгебры. Название одной из этих базовых библиотек может показаться знакомым, если вы устанавливали или компилировали одну из числовых библиотек Python, таких как SciPy и NumPy.

Линейная алгебра и статистика

Линейная алгебра является ценным инструментом в других областях математики, особенно в статистике.

Обычно студенты, изучающие статистику, рассчитывают пройти по крайней мере один семестр линейной алгебры (или прикладной алгебры) во время обучения в бакалавриате.

Влияние линейной алгебры является значительным, учитывая фундаментальную связь, которую обе области имеют с областью прикладного машинного обучения.

Некоторые наглядные примеры применения линейной алгебры в статистике и статистических методах:

• Использование векторных и матричных обозначений, особенно с многомерной статистикой.
• Решения для наименьших квадратов и взвешенных наименьших квадратов, например, для линейной регрессии.
• Оценки среднего и дисперсии матриц данных.
• Ковариационная матрица играет ключевую роль в полиномиальных гауссовых распределениях.
• Анализ основных компонентов для сокращения данных, который объединяет многие из этих элементов.

Как видите, современная статистика и анализ данных, по крайней мере, в части интересов специалиста по машинному обучению, опираются на понимание и инструменты линейной алгебры.

Применения вне геометрии

До сих пор все примеры были связаны с геометрией. Просто так проще думать: легче представить себе вращения и продолжения векторов на плоскости, чем предполагать свойства n-мерных абстрактных пространств.

Однако мы программисты и интересуемся в основном проблемами вне геометрии.

Динамическое программирование

Переходы в определенной динамике иногда могут быть выражены матричным умножением.

Рассмотрим конкретный пример. Предположим, у нас есть ориентированный граф \(G\), заданный матрицей смежности, и нам нужно найти количество путей из \(s\) в \(t\) через ровно \(k\) переходов. Размер графа мал по сравнению с \(k\) (например, несколько сотен вершин, в то время как \(k\) — число порядка \(10^\)).

Обычно мы вводим динамику \(f_\), соответствующую числу способов достижения \(v\)-й вершины ровно через \(i\) переходов. Пересчет представляет собой перечисление предпоследней вершины пути:

Оказывается, что вектор \(f_\) линейно зависит от \(f_\): его \(v\)-й элемент получается скалярным умножением \(f_\) и \(v\)-го столбца матрицы смежности \(G\) .

Поэтому выполняется следующее равенство:

(Именно поэтому \(G\) называется матрицей смежности).

Оказывается, что \(f_k\) можно расширить как \(f_k = f_0 \cdot G \cdot G \cdot \ldots \cdot G\). Поскольку умножение матриц коммутативно, мы можем применить двоичное умножение по аналогии со скалярами для вычисления \(G^k\):

Согласно этой формуле, мы должны умножить \(\log k\) на две матрицы размера \(n\), что в сумме дает \(O(n^3 \log k)\).

constintn;Матрица Бинпау(Матрица a,intp)//создаем единичную матрицуМатрица b(n,Векторint>(n,0));для(inti=0;in;i++)bii=1;в то время как(p>0)if(p&1)b=матмул(b,a);a=матмул(a,a);p>>=1;>возвратb;>

Полученная таблица в \(g_\) содержит количество путей, ведущих из вершины \(i\) в вершину \(j\), используя ровно \(k\) переходов. Ответ прост — вывести \(g_\).

• Практически не меняя сам алгоритм, можно решить задачу «с какой вероятностью мы попадём из вершины \(s\) в вершину \(t\) », если вместо булевой матрицы смежности даны вероятности, с которыми мы переходим из вершины в вершину в марковской цепи.
• Если нам не нужно количество способов, а только сам факт, можно ли дойти за ровно \(k\) переходов, то можно обернуть матрицу в битсеты и сильно ускорить решение.
• Если нас спрашивают «за не более, чем \(k\) переходов», то вместо \(k\) -той степени матрицы мы можем подобным методом посчитать сумму геометрической прогрессии.
• Эту технику можно применить и к другим динамикам, где нужно посчитать количество способов что-то сделать — иногда очень неочевидными способами. Например, можно решить такую задачу: найти количество строк длины \(k \approx 10^\), не содержащих данные маленькие запрещённые подстроки. Для этого нужно построить граф «легальных» переходов в Ахо-Корасике, возвести его матрицу смежности в \(k\) -тую степень и просуммировать в нём первую строчку.

Собственные векторы

Очень часто матрицы имеют собственные векторы — те, которые не меняют направление, когда к ним применяется матрица.

\(Av = kv\), где \(k

eq 0\). Число \(k\) называется собственным значением матрицы.

\(Av — kv = (A-kI)v = 0\) .

Линейная независимость

В общем, собственные векторы в линейной алгебре имеют почти такое же значение, как простые числа в арифметике.

Базис множества — это множество векторов, линейной комбинацией которых все векторы этого множества и только эти векторы могут быть выражены единственным образом.

Базисы существуют не только в линейной алгебре. Например, \(\) является базисом всех квадратичных троек. Или \(\) — основа всех логических выражений (т.е. все можно выразить с помощью И, ИЛИ и НЕ). Любой язык программирования может определить набор инструкций, с помощью которых можно написать что угодно, и в этом смысле также является основой.

Система векторов \(\) называется линейно зависимой, если она имеет такой набор вещественных коэффициентов \((\lambda_1, \lambda_2, \dots, \lambda_n)\), такие, что \(\lambda_j

Матрицы

eq 0\) хотя бы для одного \(j\) и \(\lambda_1 \cdot a_1 + \lambda_2 \cdot a_2 + \dots + \lambda_n \cdot a_n = 0\). В противном случае говорят, что система линейно независима. Например, базис \(N\)-мерного пространства — это линейно независимое множество \(N\)-векторов. (Доказательство: Пусть базис линейно зависим. Тогда вектор длины ноль может быть выражен по крайней мере двумя способами).

Считается, что два столбца (или две строки) матрицы линейно зависимы, если два вектора, образованные ими, линейно зависимы (склеены). Степень таблицы \(rang\) \(A\) — это максимальное число \(r\), такое, что можно выбрать \(r\) линейно независимых столбцов или строк на пару в таблице.₁Таблицы позволяют явно манипулировать конечно-размерными векторными пространствами и линейными отображениями. Поэтому их теория является важной частью линейной алгебры.₂,. v_мПусть V — конечно-мерное векторное пространство над полем F и ( v

( а 1, …, а м ) ↦ а 1 v 1 + ⋯ а м v м F м → V (a_, ldots, a_ ) и mapsto a_ v_ + cdots a_ v_ F ^ & o Vend>>

это биекция из F м, ,>набор последовательности из м элементы F, на V. Это изоморфизм векторных пространств, если F м>, v

Этот изоморфизм позволяет представить вектор его обратное изображение при этом изоморфизме, то есть вектор координат ( а 1, …, а м ), ldots, a_ )>) — базис V (таким образом, m — размерность V). Согласно определению базисной карты

Если W — другое конечномерное векторное пространство (возможно, то же самое) с базисом ( ш 1, …, ш п ), , ldots, w_ ),>линейная карта ж из W к V хорошо определяется своими значениями на базисных элементах, то есть ( ж ( ш 1 ), …, ж ( ш п ) ). ), ldots, f (w_ )).>имеет стандартную структуру векторного пространства, в котором векторное сложение и масштабное умножение выполняются на каждый компонент.

ж ( ш j ) = а 1, j v 1 + ⋯ + а м, j v м, ) = a_ v_ + cdots + a_ v_ ,>

или таблица столбцов

а 1, 1 … а 1, п ⋮ … ⋮ а м, 1 … а м, п, a_ & ldots & a_ vdots & ldots & vdots a_ & ldots & a_ end>,>

Таким образом, g может быть хорошо представлено списком соответствующих таблиц столбцов. То есть, если

для j = 1, … n, тогда g представляется матрицей

с m строками и n столбцами.

Линейные системы

Конечный набор линейных уравнений от конечного набора переменных, например, Икс 1, Икс 2 ,. .., Икс п, x_ ,. x_>Умножение матриц определяется так, что произведение двух матриц является матрицей композиции соответствующих линейных отображений, а произведение матрицы и матрицы-столбца — матрицей-столбцом, которая является результатом применения представленного линейного отображения к представленному вектору. Из этого следует, что теория конечных векторных пространств и теория матриц — это два разных языка для выражения одних и тех же понятий.

Две матрицы, которые кодируют одно и то же линейное преобразование на разных базисах, считаются подобными. Можно показать, что две матрицы похожи тогда и только тогда, когда одна из них может быть преобразована в другую с помощью элементарных операций со строками и столбцами. Для матрицы, представляющей линейное отображение из W в V, операции со строками соответствуют изменению базисов в V, а операции со столбцами — изменению базисов в W. Каждая матрица подобна унитарной матрице, возможно, ограниченной нулевыми строками и нулевыми столбцами. В терминах векторных пространств это означает, что для каждого линейного отображения из W в V существуют такие базисы, что часть базиса W отображается кратно в базис V, а остальные элементы базиса W, если они есть, отображаются в ноль. Гауссово исключение — это основной алгоритм для нахождения этих элементарных операций и доказательства этих результатов.

Линейная алгебра: пробный заезд

Или X, y ,. z называется системой линейных уравнений или линейной системой. 10 11 12 13 14

Линейные системы уравнений являются неотъемлемой частью линейной алгебры. В прошлом для решения таких систем были разработаны линейная алгебра и теория матриц. В современном представлении линейной алгебры векторными пространствами и матрицами многие задачи могут быть интерпретированы в терминах линейных систем.

Аналитическая алгебра, линейка, линейная алгебра — эти слова больше ассоциируются с фразой «сдай и забудь», чем с тем, для чего на самом деле нужна замечательная ветвь математики под названием линейная алгебра. Давайте попробуем посмотреть на него с разных сторон и выяснить, чем он хорош и почему так полезен в применении.

Начнем с практики

Первое введение в линейную алгебру часто выглядит примерно так:

Не очень вдохновляет, не так ли? Сразу же возникают два вопроса: откуда все это берется и для чего это нужно?

Когда я работал над вычислительной гидродинамикой (CFD), один коллега говорил: «Это хорошая идея: «Мы не решаем уравнения Навье-Стокса. Мы преобразуем матрицы». Фактически, линейная алгебра — это инструмент вычислительной математики:

Попробую проиллюстрировать эту взаимосвязь на более простом примере из гидродинамики._x-hПредположим, у нас есть тонкий металлический стержень с закрепленными концами, температура которого поддерживается равной нулю. Начнем нагревать стержень с помощью распределенного источника тепла, который излучает q(x) джоулей в секунду на единицу длины стержня вблизи точки x. Какая температура t=t(x) определена? Давайте сделаем очень грубый набросок модели. При достижении равновесия, для каждого сегмента x-h, x+h нашего стержня, тепловой поток источника должен быть равен сумме тепловых потоков через границы сегментов. Если h достаточно мало, то это уравнение можно записать в константах (в которые входит h, да простят меня читатели)_x+hгде Q

— тепловой поток на левой границе, а Q_i— через правую границу. Согласно закону Фурье, тепловой поток пропорционален разнице температур (когда вы ныряете в бассейн, в первые несколько секунд он самый холодный). Поэтому (с точностью до констант, содержащих h)._iПусть h = 1/N. Рассмотрим точки вида x_i= i — h, где i = 0, 1, 2,. N. Они называются сетками. Тогда переменные t

=t(x_i) удовлетворяют уравнениям_iгде мы уже рассмотрели граничные условия, и q

• записать систему в короткой форме A · y = b (вот откуда взялось умножение матриц!);
• понять, имеет ли она решение и единственно ли оно;
• (в данном примере) найти его с помощью простой формулы y = A -1 b, как будто A — число;
• (перетекая в вычислительную математику) построить эффективные численные методы решения систем линейных уравнений.

=q(x )

). Таким образом, мы имеем систему линейных уравнений:_ijВ качестве другого примера приведу хорошо известную проблему, связанную с ранжированием страниц на сайте (или в Интернете в целом) по количеству ссылок. У вас есть N страниц, каждая из которых может содержать ссылки на другие страницы. Вам необходимо определить, какие страницы являются наиболее важными. То, как именно мы измеряем «важность», является частью проблемы. Количественно представим его в виде неотрицательного числа (веса). Мы делаем естественное предположение: Чем больше ссылок указывает на определенную страницу, тем больше ее вес. Однако у этого подхода есть недостаток: мы не учитываем вес связанных страниц. Логично предположить, что ссылка со страницы с большим весом должна иметь более высокую ценность. Это соображение приводит нас к следующей модели

где а

Теперь немного теории

— это количество ссылок на страницу i со страницы j, деленное на общее количество ссылок со страницы j. Эта формула может быть прочитана следующим образом: Вес страницы i равен произведению веса страницы j, деленного на долю ссылок со страницы j на страницу i. Таким образом, мы свели нашу проблему к набору страниц i. Более того, весовой вектор p оказывается собственным вектором матрицы A, что соответствует собственному значению 1:

Существование этого вектора (строго говоря, для слегка модифицированной матрицы A ) гарантируется теоремой Фробениуса-Перрона. И его можно найти методом простых итераций.

Линейная алгебра изучает векторные пространства и функции, которые отображают одно векторное пространство на другое. В основном рассматриваются линейные функции (которые удовлетворяют соотношению f(a — x + b — y) = a — f(x) + b — f(y) для произвольных чисел a и b и произвольных векторов x и y). Существуют также нелинейные формы (например, квадратичные формы). Но сначала нужно понять, что такое вектор (и векторное пространство). И это не так тривиально, как кажется.

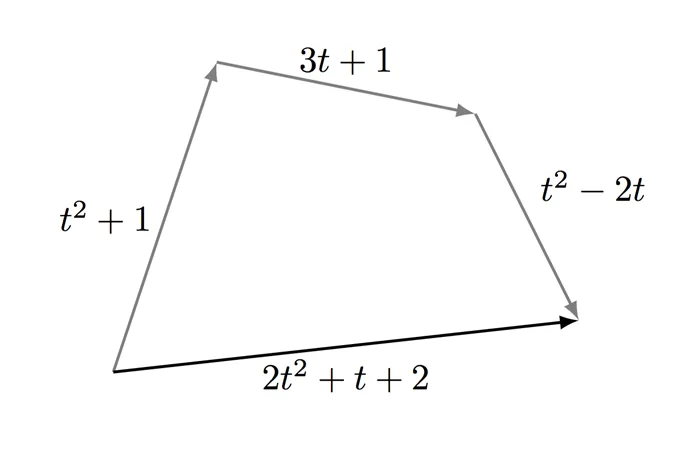
В учебниках и курсах обычно дается абстрактное определение из 8 пунктов. Иногда также говорят, что векторное пространство — это аддитивно записываемая абелева группа, в которой скалярное умножение определено и удовлетворяет 4 аксиомам. Однако для студентов первого курса линейной алгебры это совсем не полезно. Гораздо проще посмотреть на конкретные примеры и увидеть в них аналогию. А определение из 8 пунктов — это просто формализация этой аналогии. Итак, перейдем непосредственно к примерам.₁, x₂,. x_nКонечно, направленные отрезки, которые все знают со школы, — это векторы. Множество направленных отрезков является примером векторного пространства. Теперь давайте рассмотрим многочлены. Их можно складывать и умножать на числа. Примечание: С алгебраической точки зрения, эти операции сложения многочленов и умножения многочлена на число работают по тем же правилам, что и для направленных отрезков. Например, равенство x+y = y+x (коммутативность) применимо как к направленным отрезкам, так и к многочленам. Поэтому множество полиномов является векторным пространством, а полиномы — векторами.₁, α₂,. α_nПоскольку полиномы подобны направленным отрезкам, они также должны иметь координаты. Но как их найти и сколько координат в многочлене? Известно, что каждый вектор имеет ровно две координаты на плоскости и три координаты в пространстве. Почему так происходит? И что такое размерность вообще? Линейная алгебра дает ответ на этот вопрос: размерность — это максимальное количество линейно независимых векторов. Что вы понимаете под линейной независимостью? Векторы x

называются линейно независимыми, если у нас есть числа a

из которых хотя бы один не равен нулю, так что₁, x₂,. x_nЕсли векторы не являются линейно зависимыми, они называются линейно независимыми. (Понятие линейной зависимости обобщает понятия параллельных и сопараллельных векторов: два вектора линейно зависимы тогда и только тогда, когда они параллельны. Три вектора линейно зависимы тогда и только тогда, когда они совпадают).₁, x₂,. x_nРазмерность пространства может быть либо конечной (пространство многочленов со степенью не выше N), либо бесконечной (пространство всех многочленов). На практике встречаются оба случая, но давайте ограничимся конечными размерами. Пусть векторы x

линейно независимы, а n — размерность пространства. Тогда каждый другой вектор x может быть записан как линейная комбинация x

Приложения

уникальным образом. Коэффициенты соответствующей линейной комбинации и называются координатами.

Теперь у нас есть строгое определение координат. Но дело не только в этом: на этом пути мы сталкиваемся с более базовыми (и менее заметными) понятиями, такими как линейная комбинация и линейная зависимость. Также мы узнаем, что в n-мерном линейном пространстве не может быть более n линейно независимых векторов. Этот факт является одним из краеугольных камней линейной алгебры.

Исторический очерк

Евклидовы пространства, аффинные пространства и многие другие пространства, изучаемые в геометрии, определяются как векторные пространства. Автоморфизмы векторного пространства над леммой образуют группу в смысле умножения, изоморфную группе невырожденных квадратичных матриц, что связывает линейную алгебру с теорией групп и, в частности, с теорией представлений линейных групп 2.

Переход от n-мерных векторных пространств, используемых в линейной алгебре, к бесконечным линейным пространствам отражен в некоторых разделах функционального анализа 1.

Исторически первым вопросом линейной алгебры был вопрос Декарта и Фермата 1636) источник не указан 3622 дня. Построение теории матриц, классы 1 2. В 1750 году он предложил 2. для решения систем линейных уравнений.

См. также

1. ↑ 1,01,11,2Линейная алгебра. Большая советская энциклопедия.В двадцатом веке векторное пространство становится основным объектом изучения в линейной алгебре 2.В 1833 году он воспроизвел комплексные числа в двумерном реальном векторном пространстве, как мы бы назвали его сегодня, и известен открытием кватернионов и введением термина «вектор». Теория матриц была разработана в работах Кейли (1850-е годы). Системы линейных уравнений в матрично-векторной форме впервые появились, по-видимому, в работах 1867 года). 1844 и 1862 годах исследованиями того, что мы бы сейчас назвали Пеано (1888) источник не определил 3622 дня.
2. ↑ 2,02,12,22,32,4 Виноградов И. М. Линейная алгебра // Математическая энциклопедия. — М .: Советская энциклопедия, 1977. (см. ISBN )

• Мальцев А. И. Основы линейной алгебры. М.: Наука, 1975.
• Гельфанд И. М. Лекции по линейной алгебре М.: Наука, 1971.
• Фаддеев Д. К. Лекции по алгебре. М.: Наука, 1984.
• Кострикин А. И. Введение в алгебру, Ч. 2: Линейная алгебра. М.: МЦНМО, 2009.
• В. А. Ильин, Э. Г. Позняк Линейная алгебра, М.: Наука — Физматлит, 1999.
• В. А. Ильин, Г. Д. Ким Линейная алгебра и аналитическая геометрия, М.: ТК Велби, Изд-во Проспект, 2007, 400с.
• Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. — М .: ФИЗМАТЛИТ, 2002. — 248 с. (см. ISBN )

• Линейная алгебра. Курс лекций.
• Ефимов Н. В., Розендорн Э. Р. Линейная алгебра и многомерная геометрия.-М.:Наука 1969, 528с.
• Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия.-СПб.: Лань 2005, 304с.
• Курош А. Г. Курс высшей алгебры.-М.:Наука 1968, 331с.
• Ланкастер П. Теория матриц.-М.:Наука 1973, 280с.
• Проскуряков И. В. Сборник задач по линейной алгебре.-М.:Наука 1966, 384с.
• Стренг Г. Линейная алгебра и ее применения.-М.:Мир 1980, 454с.
• Фаддеев Д. К., Фаддеева В. Н. Вычислительные методы линейной алгебры.- 356с.
• М .: Мир, 1989, 655 с., ил. (ISBN 5-03-001042-4).
• Шилов Г. Е. Математический анализ (Конечномерные линейные пространства).- 264с.
• Матричный анализ и линейная алгебра. Курс лекций для студентов факультета ВМК, МГУ.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия, — Физматлит, Москва, 2009.
• Шарипов Р. А., Курс линейной алгебры и многомерной геометрии, — БашГУ, Уфа, 1996.

Определитель и его вычисление для матриц второго и третьего порядков

Проверено 20 декабря 2012 года.

Архивировано из первоисточника 27 декабря 2012.

Рассмотрим квадратную матрицу порядка n:

Составьте произведение элементов этой матрицы, по одному из каждой строки и каждого столбца. Если отсортировать элементы этого произведения в порядке возрастания номера строки, то его можно записать в виде:

Номера столбцов в записанном продукте являются перестановкой чисел 1, 2, …, n.

Определение: число, равное сумме всех произведений n!

является определителем квадратной матрицы A (определитель n-го порядка) и обозначается |A| или det A. В расширенном виде определитель записывается следующим образом

Используя это определение, мы можем найти выражение для определителей второго и третьего порядка.

С сайта

Чтобы вычислить детерминант третьего порядка, нам нужно подсчитать количество разворотов в каждой перестановке 1, 2, 3 :

Затем

Для упрощения вычисления определителя третьего порядка можно применить правило треугольника, согласно которому при символе » + » мы должны получить произведения в соответствии с рисунком

и с символом » — » » — в соответствии со схемой

Свойства определителя

Пример 3

Решение. Воспользуемся правилом треугольников:

1) Если в любой строке (столбце) определителя есть нули, то определитель равен нулю.

2) Общий множитель элементов любой строки (столбца) может быть передан через знак определителя.

3) Если все элементы любой строки/столбца определителя равны суммам двух слагаемых, то этот определитель является суммой двух определителей с соответствующими первым и вторым слагаемыми в этой строке/столбце, а остальные элементы обоих определителей те же, что и в исходном определителе.

Эти свойства следуют непосредственно из определения идентификатора.

4) Если переставить местами любые две строки (столбцы) определителя, то знак меняется на противоположный.

Например, переставьте две строки определителя. В результате мы имеем определитель, в котором каждый член имеет другой знак, чем соответствующий член исходного определителя, поскольку, как показано в Лемме 1, четность соответствующей перестановки вторых индексов меняется на противоположную.

Обратная матрица

5) Если любые две строки (столбца) определителя совпадают (пропорциональны), то определитель равен нулю.

А именно, если две строки (столбца) в определителе совпадают, то, с одной стороны, определитель не меняется, а с другой — его знак меняется на противоположный в соответствии с предыдущим свойством. Поэтому |A| = — |A| и, следовательно, |A| = 0. Если определитель имеет две одинаковые строки (столбцы), то после переноса его знака по свойству 2) на общий множитель элементов строки (столбца) получается определитель с двумя одинаковыми строками (столбцами), который равен нулю.

Определение.

Из этого определения следует, что матрица A-1 также является квадратной матрицей той же размерности, что и матрица A.

Отметим некоторые свойства обратной матрицы, вытекающие из ее определения.

α) Матрица не может иметь более одной обратной матрицы.

Предположим, что для матрицы A существуют две обратные матрицы.

Умножьте обе части первого уравнения слева на матрицу

(c) Если для матрицы A и матрицы B одного порядка существует обратная, предположим, что матрица AB также имеет обратную, и

Найдем условия, при которых обратная матрица существует.

Теорема (критерий существования обратной матрицы). Если обратная матрица существует, то необходимо и достаточно, чтобы матрица была невырожденной, т.е. ее определитель был ненулевым.

Доказательство. Сначала докажем необходимость теоремы. Предположим, что существует обратная матрица для матрицы A. Тогда равенство AA-1 = E, используя свойство 10) определителя матричного произведения, дает: det(AA-1) = det A 0.

Теперь мы хотим проверить, является ли условие теоремы также достаточным. Предположим, что матрица A не является вырожденной. Проверим, что обратной этой матрицей является матрица со следующей структурой: 1:

Действительно, если

где, используя свойства 7) и 9) определителя (§2, п. 3), заключаем:

т.е. AA-1 = E. Отсюда следует, что AA-1A = E. Предложение доказано.

Строки приведенной ниже таблицы содержат алгебраические дополнения к элементам соответствующих столбцов.

Пример №6

Найдите обратную сторону матрицы

Решение. Сначала определите детерминант матрицы:

Следовательно,

Обратную сторону матрицы можно использовать для решения линейных матричных уравнений. Например, предположим, что нам нужно решить матричное уравнение

Ранг матрицы и его вычисление

с известными матрицами A и B, где матрица A не является вырожденной. Умножив обе части этого матричного уравнения влево на обратную часть матрицы A-1, получим:

Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а решением матричного уравнения AXB = C с невырожденными матрицами A и B является матрица X = A-1CB-1.

Рассмотрим любую матрицу

Минором порядка k матрицы A называется определитель, берущий пересечение выбранных k строк и k столбцов этой матрицы.

Определение: Степенью матрицы A называется максимальный из ненулевых порядков миноров этой матрицы. Степень обозначается rang A.

Очевидно предположить, что диапазон O = 0. Также очевидно, что

Пример #7

Найдите ранг матрицы

Решение. Вычислим минор на пересечении первых двух строк и первого и четвертого столбцов:

Все нули третьего порядка этой матрицы равны нулю, так как третья строка равна разности между второй и первой строками. Следовательно, диапазон A = 2

1. перестановка двух строк (столбцов) матрицы;
2. умножение строки (столбца) на ненулевое действительное число;
3. добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.

Как видно из определения, вычисление ранжирования матрицы по минору является очень трудоемкой задачей, особенно для матриц большой размерности. Другой метод, основанный на элементарных преобразованиях матрицы, позволяет значительно сократить вычислительные затраты.

Элементарными преобразованиями таблицы являются следующие операции над ее строками или столбцами:

Тот факт, что таблица B получается из таблицы A путем одного или нескольких последующих элементарных преобразований, доказывается следующим образом.

Теорема. Степень матрицы не изменяется при ее элементарных преобразованиях.

Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что в силу свойств 2) и 4) определителя (§2, п. 3), миноры исходной матрицы могут отличаться от миноров преобразованной матрицы только знаком или ненулевым множителем, что, конечно, не влияет на ранг матрицы. Теперь предположим, что матрица A’ получена из матрицы A третьим элементарным преобразованием; для определенности предположим, что к строке с номером i прибавляется строка с номером j, умноженная на действительное число (если такого минора нет, то rank В обоих случаях, согласно определению порядка матрицы, минор M равен 0. Следовательно, диапазон A’ равен n.

Достаточность:

Вывод: чтобы однородная система из n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее главный определитель был равен нулю.

Доказательство:

При копировании материалов с сайта evkova.org активная ссылка на www.evkova.org обязательна.

Сайт создан группой педагогов на некоммерческой основе для дополнительного образования молодежи.

Сайт создан, поддерживается и управляется командой педагогов