Круг разрезается на 10 частей. Правила такие же, как и в других играх: Все 10 деталей должны быть использованы для формирования силуэта, не перекрывая друг друга. Вырезанный круг должен иметь одинаковый цвет с обеих сторон.
Информация
Тест на логическое мышление и распознавание образов. Картинки-задания состоят из комбинации различных фигур, нужно определить принцип, по которому они расположены, необходимо завершить последовательность. Каждый вопрос содержит 5 ответов, из которых только 1 правильный. Время не ограничено, поэтому внимательно смотрите на картинку, определяйте порядок и отвечайте медленно. Вы получите правильный ответ с подробными объяснениями.
Вы уже сдавали экзамен один раз. Вы не можете принять его снова.
Чтобы начать тест, необходимо войти в систему или зарегистрироваться.
Чтобы начать эту викторину, вы должны ответить на следующие вопросы викторины:
Результаты
Правильные ответы: 0 из 5
Вы набрали 0 очков из 0 возможных ( 0 )
1 .
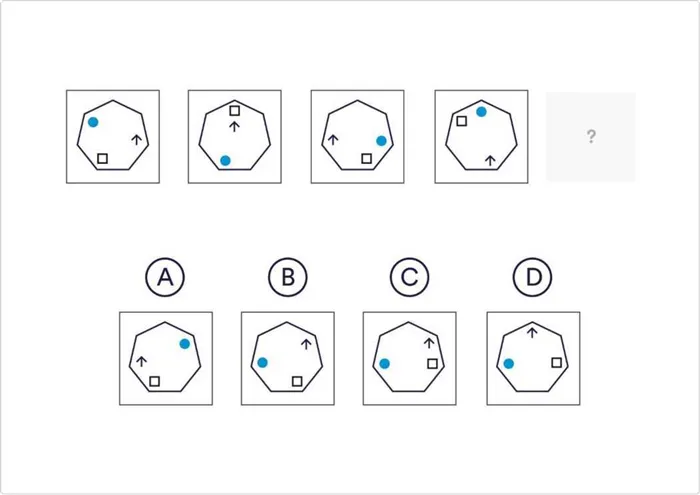
Какое из следующих чисел завершает последовательность?
Правильно! Рад за тебя. Фигуры перемещаются вокруг центра в вершинах многоугольника. Круг и стрелка двигаются на 2 шага против часовой стрелки, квадрат — на 4 шага по часовой стрелке.
Ответ: Γ. Фигуры перемещаются вокруг центра в вершинах многоугольника. Круг и стрелка двигаются против часовой стрелки за 2 шага, а квадрат — по часовой стрелке за 4 шага.
2 .
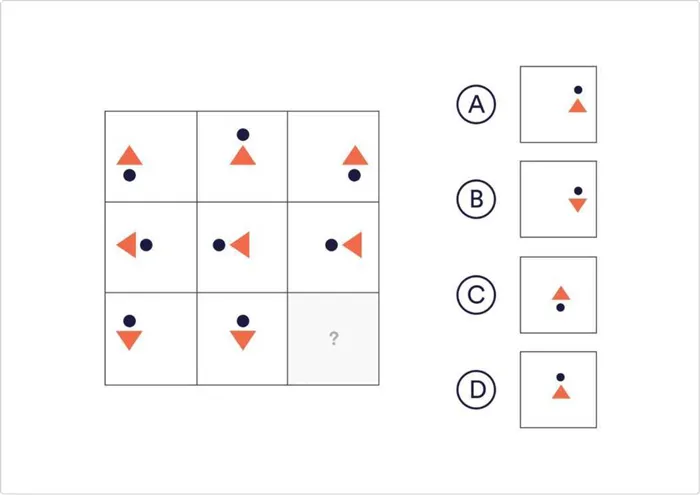
Какое из следующих чисел завершает последовательность?
Правильно! Молодец. Треугольник — самая важная фигура, на которую следует обратить внимание. Он изменяет свое положение относительно квадрата клетки. В левой колонке треугольник находится на левой стороне, в средней колонке — посередине, а в правой колонке треугольник должен быть на правой стороне. Далее посмотрите, как треугольник располагается ряд за рядом.
Ответ: Β. Треугольник — самая важная фигура, на которую следует обратить внимание. Он изменяет свое положение относительно квадрата клетки. В левой колонке треугольники расположены слева, в средней колонке они центрированы, поэтому в правой колонке треугольник должен располагаться справа. Далее рассмотрим, как треугольник расположен в рядах.
3 .
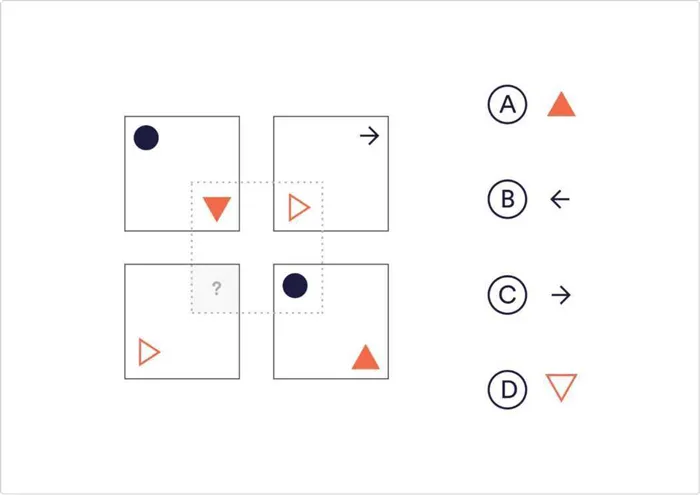
Какое из следующих чисел завершает последовательность?
Точно! Молодец. Числа внутри пунктирного квадрата соответствуют внешним углам противоположных квадратов по диагонали. Формы внешних верхних квадратов отражаются во внутренних нижних квадратах.
Ответ: Γ. Числа внутри пунктирного квадрата соответствуют номерам внешних углов противоположных квадратов по диагонали. Числа во внешних верхних квадратах отражаются во внутренних нижних квадратах.
4 .
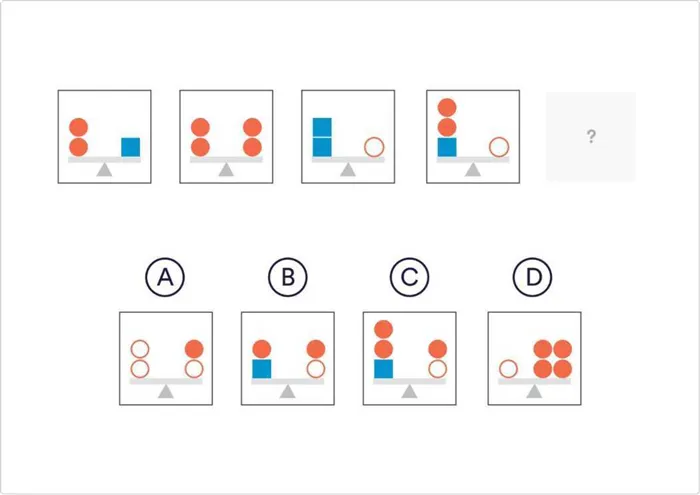
Какое из следующих чисел завершает последовательность?
Правильно! Браво. Нам необходимо определить баланс различных элементов. На первом рисунке 2 оранжевых круга соответствуют синему квадрату. 2 синих квадрата соответствуют белому кругу. Итак: 1 белый круг = 2 синих квадрата = 4 оранжевых круга. Кроме того, оранжевый круг и синий квадрат появляются три раза, поэтому должен быть один белый круг.
Ответ. На первом рисунке 2 оранжевых круга соответствуют синему квадрату. Два синих квадрата равны белому кругу. Итак: 1 белый круг = 2 синих квадрата = 4 оранжевых круга. Кроме того, оранжевый круг и синий квадрат появляются три раза, поэтому должен быть белый круг.
5 .
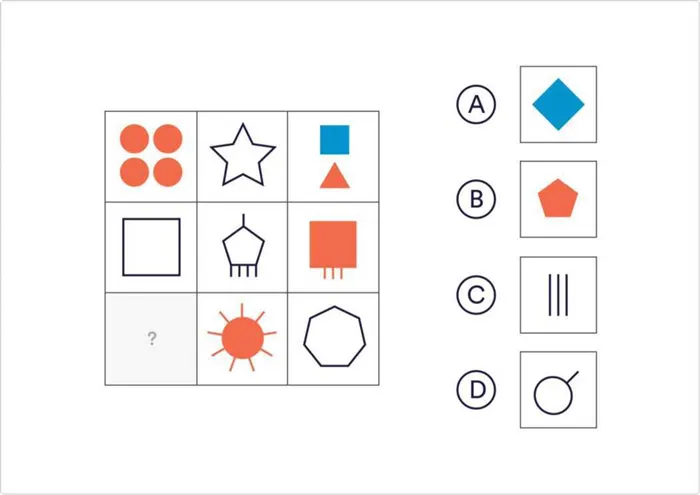
Какое из следующих чисел завершает последовательность?
Начерти фигуры, состоящие из данного количества клеток : 10, 17, 30, 36, 80, 99, 100, 103, 128, 200, 206?
Нарисуйте фигуры, состоящие из заданного количества квадратов: 10, 17, 30, 36, 80, 99, 100, 103, 128, 200, 206.
Добавьте к списку вопросов изображение того, что необходимо решить.
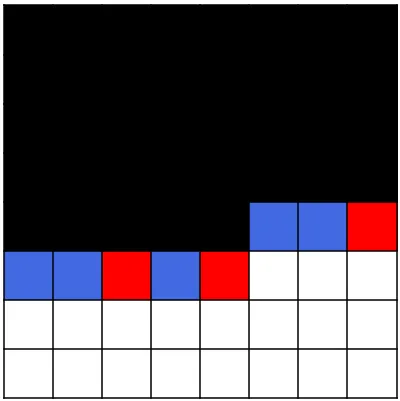
Нарисуйте в тетради фигуру, составленную из 10 полосок по 10 квадратов, сколько квадратов имеет эта фигура?
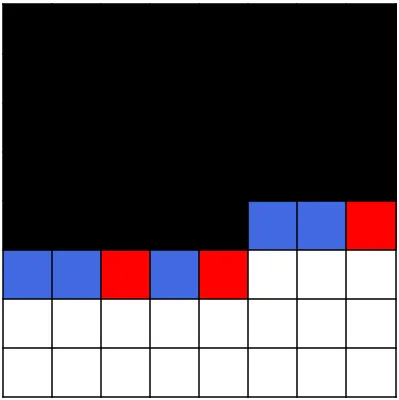
Сколько клеток содержит каждая форма?
Найдите равное число между данными числами.
Нарисуйте оставшиеся фигуры в блокноте и заполните их так, чтобы они были одинакового размера.
Замощение с помощью решения задачи о максимальном паросочетании
Возвращаясь к черно-белой раскраске, мы можем наблюдать интересную интерпретацию проблемы домино, как на шахматной доске. Рассмотрим граф, в котором квадраты фигуры являются вершинами, ребра соединены с квадратами, имеющими общую сторону. Таким образом, домино в этом графе — это просто ребро. Если мы раскрасим график в шахматном порядке, то внезапно поймем, что этот график бимодальный: черный цвет — это одно ребро, а белый — другое. Когда мы переформулируем задачу размещения наибольшего количества клеток на основе этого графа, нам нужно найти максимальное количество ребер так, чтобы вершины были ребрами не более чем одного ребра. В целом, это достаточно хорошо известная проблема максимального соответствия. Давайте попробуем применить его к этой проблеме, он работает даже с мультфильмами, я привожу базовый алгоритм Куна для нахождения максимального совпадения в паре.
Применение алгоритма Куна для установления соответствия на графе домино.
def check_valid(i, j, n, m, tiling): return 0Здесь мы можем даже анимировать процесс
sequential_match = match_with_flow(tiling_custom)Суть алгоритма Куна (и любого другого алгоритма поиска максимальной пары) заключается в поиске "инкрементных путей". С точки зрения домино, это цепочка домино с двумя пустыми клетками на каждом конце. Такие цепочки могут быть заменены более крупными цепочками, включающими те же ячейки и заполняющими две пустые ячейки на концах цепочки. Более того, основное утверждение, на котором основаны все алгоритмы поиска максимального соединения, заключается в том, что если такая цепочка не может быть найдена, то мы не можем получить большую плитку.
UPD. В последнем примере простое обоснование, основанное на черном и белом, не работает. Насколько я знаю, существует два общих критерия для полной укладки плитки:
- Теорема Холла (теорема о свадьбах) Проверка условий этой теоремы вычислительно сложнее, чем построить максимальное паросочетание.
- Условие высоты Тёрстона про это я мало что знаю
Недавно я наткнулся на очень интересную статью о тайлингах, в которой, среди прочего, обсуждается, как использовать группы для доказательства того, что другой тайлинг невозможен.
Бонус! Раскраска планарного графа в 5 цветов.
Для иллюстрации плитки я использовал разные цвета для каждого домино. К сожалению, некоторые цвета выглядят не очень хорошо, а некоторые плохо контрастируют. В этом случае выбрать цвета для хорошего контраста непросто, особенно если доминошек много. Однако можно использовать и меньшее количество цветов: Домино, которые не находятся рядом друг с другом, могут быть окрашены в один цвет, чтобы визуально было понятно, как выглядит покрытие. В общем, это классическая проблема раскраски узлов плоского графа. Любой планарный граф можно раскрасить 4 цветами, но хорошего алгоритма для такой раскраски не существует. Но есть простой алгоритм для раскрашивания в 5 цветов, хотя это все еще много, и я не пробовал его (если требуется 5-й цвет, то, скорее всего, будут ошибки).
def color_5(filling): result = i for i in row for row in filling # Строим граф domino_tiles = for i in range(max(map(max, filling)) + 1) domino_neighbours = set() for i in range(max(map(max, filling)) + 1) degree = 0 for i in range(max(map(max, filling)) + 1) n = len(filling) m = len(filling0) for i, row in enumerate(filling): for j, num in enumerate(row): if num>= 0: domino_tilesnum.append((i, j)) for i, tiles in enumerate(domino_tiles): for x, y in tiles: for dx, dy in (-1, 0), (1, 0), (0, -1), (0, 1), (-1, -1), (-1, 1), (1, -1), (1, 1): a, b = x + dx, y + dy if 0 = 0 and fillingab != i \ and fillingab not in domino_neighboursi: domino_neighboursi.add(fillingab) degreei += 1 # Первым делом нужно найти такой порядок вершин, все вершины имели не больше 5 соседей среди # предыдущих. Такой существует в силу того, что граф планарный, а найти его эффективнее всего # по очереди находя вершину наименьшей степени и удаляя её из графа, так мы получаем обратный порядок active_degrees = set() for i in range(max(degree) + 1) for i, deg in enumerate(degree): active_degreesdeg.add(i) reversed_order = for step in range(len(domino_tiles)): min_degree = min(i for i, dominoes in enumerate(active_degrees) if len(dominoes)>0) domino = active_degreesmin_degree.pop() reversed_order.append(domino) for other in domino_neighboursdomino: if other in active_degreesdegreeother: active_degreesdegreeother.remove(other) degreeother -= 1 active_degreesdegreeother. add(other) # Теперь идем в обратном порядке и либо закрашиваем другой незанятый цвет # если осталось 5 цветов, либо находим цепочку чередующихся цветов # которые можно перекрасить. Это найдено из-за плоской формы colors = -1 for domino in domino_tiles slices = draw_filling(result) for domino in reversed(reversed_order): used_colors = colorsother for other in domino_neighboursdomino if colorsother != -1 domino_color = len(used_colors) for i, color in enumerate(sorted(set(used_colors))): if i != color: domino_color = i break if domino_color<5: colorsdomino = domino_color for x, y in domino_tilesdomino: resultxy = domino_color slices.append(draw_filling(result)) continue # Начиная отсюда код я не тестировал, не нашел примера c = 0 other = other for other in domino_neighboursdomino if colorsother == c visited = set(other) q = Queue() q.put(other) domino_was_reached = False while not q.empty(): cur = q.get() for other in domino_neighbourscur: if other == domino: domino_was_reached = True break if colorother == c or colorother == c + 1 and other not in visited: visited.add(other) q.put(other) if not domino_was_reached: for other in visited: colorother = colorother ^ 1 for x, y in domino_tilesother: resultxy = colorother colordomino = c for x, y in domino_tilesdomino: resultxy = c slices.append(draw_filling(result)) continue # Проделываем тоже самое для 2 и 3. c = 2 other = other for other in domino_neighboursdomino if colorsother == c visited = set(other) q = Queue() q.put(other) domino_was_reached = False while not q.empty(): cur = q.get() for other in domino_neighbourscur: if other == domino: domino_was_reached = True break if colorother == c or colorother == c + 1 and other not in visited: visited.add(other) q.put(other) for other in visited: colorother = colorother ^ 1 for x, y in domino_tilesother: resultxy = colorother colordomino = c for x, y in domino_tilesdomino: resultxy = c slices.append(draw_filling(result)) return result, slicesЕсли вы хотите использовать этот код, обратите внимание, что каждый шаг там рендерится - это было необходимо для анимации, которая сильно замедляет алгоритм. Если вам нужно только конечное изображение, удалите весь код, содержащий переменную slices.
Настольная игра
Пентамино также можно использовать как настольную игру для двух игроков. 7 Для игры вам понадобится шахматная доска 8×8 и набор фигур Пентамино, квадраты которых такого же размера, как и квадраты на шахматной доске. В начале игры доска пуста. Игроки по очереди выставляют фигуру на доску, закрывая 5 пустых клеток на доске. Все размещенные фигуры остаются на месте до конца игры (они не удаляются и не перемещаются с доски). Проигрывает тот игрок, который не может сделать больше ни одного хода (либо потому, что ни одна из оставшихся фигур не осталась на пустых клетках доски, либо потому, что все 12 фигур уже были расставлены на доске).
Анализ игры довольно сложен (например, в начале существует даже больше возможных первых ходов, чем в шахматах). Голомб предложил следующую стратегию: Постарайтесь разделить свободное пространство на доске на две равные области (и не дать это сделать своему противнику). После этого на каждый ход противника в одной из областей следует отвечать ходом в другой области.
Пример игры в пентамино показан на рисунке. Нумерация ходов последовательная (ходы с нечетными номерами принадлежат первому игроку, ходы с четными номерами принадлежат второму игроку). В начале игроки делают свои ходы в середине доски (ходы 1-3), чтобы не дать другим игрокам разделить доску на равномерно распределенные позиции. Но затем второй игрок делает неудачный ход (ход 4), который позволяет его противнику разделить пустой квадрат на два квадрата по 16 (ход 5). (В данном примере пустые квадраты не только равны по площади, но и совпадают по форме - они симметричны относительно диагонали доски, но, конечно, это не обязательно для стратегии). На ход второго игрока (6) в одной из этих областей, первый игрок отвечает ходом в другой области (7) и выигрывает. Хотя на доске еще есть три пустых места с пятью или более клетками, все фигуры (I, P, U) уже используются.
Варианты настольной игры
Пентамино с заранее выбранными фигурами
В этом варианте игры игроки сначала по очереди выбирают по одной фигуре, пока все фигуры не будут разделены между ними. Далее игра ведется по обычным правилам Пентамино, с той лишь разницей, что каждый игрок может передвигаться только теми фигурами, которые он выбрал. Игрок, взявший последнюю фигуру, делает первый ход.
Стратегия Голомба в этом варианте игры значительно отличается от стратегии обычного пентамино. Вместо того чтобы делить доску на равномерно распределенные фигуры, Голомб пытается создать на доске области, которые могут быть заполнены только его фигурами, но не фигурами его противника. (Голомб называет эти зоны "бункерами").
Пример игры в пентамино со стандартными фигурами показан на рисунке. Фигуры, выбранные первым и вторым игроком, перечислены слева и справа от доски. Зачеркнутая буква означает, что деталь была использована для перемещения. Сначала игроки избавляются от "самых неудобных" фигур X и W (ходы 1 и 2), затем первый игрок создает "убежище" для Y (ход 3), а второй игрок - для U и P (ходы 4 и 6). Эти "убежища" заполняются в конце игры (ходы 8-10), и игра заканчивается победой второго игрока - у первого игрока есть Т-образный пятиугольник, для которого больше нет свободного места на остальной части доски.
Другие варианты
- «Карточное пентамино» — вариант игры с привнесением случайных событий. Фигуры пентамино (или их буквенные обозначения) рисуют на карточках, которые тасуют и раздают игрокам. Игроки выбирают фигуры в соответствии с розданными им карточками. Далее игра идёт по правилам пентамино с заранее выбранными фигурами.
- Пентамино для четырёх игроков. Четыре игрока, сидящие по четырём сторонам доски, играют двое на двое (игроки, сидящие друг напротив друга, образуют команду). Проигравшей считается команда, игрок которой первым не сможет сделать хода. В эту игру можно играть по любому из трёх вышеописанных вариантов — обычному, с заранее выбранными фигурами или «карточному».
- «Кто-кого?» В игре участвует от двух до четырёх игроков, но каждый из них играет только за себя. Победителем считается сделавший последний ход, ему засчитывается 10 очков. Игрок, который должен ходить после победителя (т.е. первым не сможет сделать хода) получает 0 очков, а все остальные игроки — по 5 очков. Может быть сыграно несколько партий, набранные в них очки суммируются. Игра также может проводиться по любому из трёх вышеописанных вариантов правил.
Ссылки
- Клуб любителей пентамино — можно прочесть правила, скачать компьютерную версию игры
- BANJEN Pentamino — реализация игры
| Полиформы | |
|---|---|
| Полиформы | Домино - Трине - Квад - Пентамино - Гекс - Семь - Восемь - Девять |
| Другое | Коннект (игрушка) - Полиаболо - Поликуб - Полидрафтер - Полигекс - Полиалмаз - Полиаминоид - Полистик |
| Тетрис | |
|---|---|
| Главная страница |
Алексей Пажитнов - Эффект Тетриса - Тетрамино - The Tetris Company Tetris: The Soviet Mind Game - Tetris Plus - Tetris Plus 2 - Tetris: The Grandmaster - Magic Tetris Challenge - Tetris 64 - The New Tetris - Tetris Worlds - Tetris Splash - Tetris Party Тетрис (Game Boy) - Тетрис (iOS) - V-Тетрис - 3D Тетрис - Тетрис DS - Тетрис 3DS Blockout - Welltris - Hatris - Wordtris - Tetris Attack - TetriNET - Tetrisphere - KDE Games KBlocks/KSirtet - Quadrapassel Фонд Викимедиа. 2010 . ПолезноеСмотреть что такое "Пентамино" в других словарях:
ДоминоДомино состоит из двух квадратов и может иметь только одну форму - прямоугольник размером 1×2 (см. рис. 1). Первая проблема, связанная с домино, наверняка знакома многим: Рассмотрим шахматную доску, на которой нарисованы пара противоположных угловых квадратов и коробка домино, каждый из которых покрывает ровно две клетки шахматной доски (см. рис. 2). Можно ли покрыть всю доску 31 домино (без свободных квадратов и перекрытий)? Ответ на этот вопрос - "НЕТ" и имеет замечательное доказательство. Шахматная доска состоит из 64 чередующихся белых и черных квадратов (имеется в виду типичная расцветка шахматной доски). Каждая доминошка, поставленная на такую доску и покрывающая две соседние клетки, покрывает одну белую и одну черную клетку, а n доминошек покрывают n белых и n черных клеток, т.е. их одинаковое количество. Однако показанная шахматная доска содержит больше черных квадратов, чем белых, и поэтому не может быть покрыта домино. Этот результат является стандартной теоремой комбинаторной геометрии. Тримино (или триомино) - это полимино третьего порядка, т.е. многоугольник, образованный соединением трех равных квадратов, соединенных сторонами. Если вращения и отражения не рассматривать как различные формы, то существует только две "свободные" формы тримино (см. рисунок 3): прямая (рисунок I) и угловая (рисунок L). ТетраминоС тримино связано много проблем, связанных с конструированием их различных форм. Оказывается, что из полного набора тримино невозможно построить ни одного прямоугольника. Доказательство осуществляется путем раскрашивания шахматных узоров. Все квадраты, кроме Т-образного, содержат 2 черные клетки и 2 белые клетки, а Т-образный квадрат содержит 3 клетки одного цвета и 1 клетку другого цвета. Поэтому каждая фигура полного набора тетраминоидов (см. рисунок 4) содержит на две клетки одного цвета больше, чем другого. Но каждый прямоугольник с четным количеством клеток содержит равное количество черных и белых клеток. Рисунок 5 Многомино, которое покрывает пять квадратов шахматной доски, называется пентомино. Существует 12 типов пентамино, которые могут быть названы латинскими заглавными буквами, как показано на рисунке (см. Рисунок 5). Чтобы нам было легче запомнить эти имена, в конце латинского алфавита указаны соответствующие буквы ( TUVWXYZ ) и введено имя FiLiPiNo. Поскольку всего существует 12 различных пентаминоидов и каждый из этих элементов охватывает пять клеток, всего имеется 60 клеток. Самая распространенная задача пентамино - составить прямоугольник из всех фигур без наложений и зазоров. Поскольку каждая из 12 фигур содержит 5 квадратов, площадь прямоугольника должна составлять 60 единичных квадратов. Возможные прямоугольники - 6×10, 5×12, 4×15 и 3×20 (см. рис. 6). Рисунок 6. Для случая 6×10 эта проблема была впервые решена Джоном Флетчером в 1965 году. Существует ровно 2339 различных расположений пентаминоидов в прямоугольнике 6×10, не считая вращений и отражений всего прямоугольника, а считая вращения и отражения его частей (иногда внутри прямоугольника образуется симметричная комбинация фигур, вращение которой может дать дополнительные решения). Для прямоугольника 5×12 существует 1010 решений, для прямоугольника 4×15 - 368 решений, а для прямоугольника 3×20 - всего 2 решения (которые отличаются описанным выше поворотом). В частности, существует 16 способов сложить два прямоугольника 5×6, которые можно использовать для формирования прямоугольников 6×10 и 5×12. Еще одна интересная проблема пятиугольника - проблема тройного пятиугольника (см. рис. 7), предложенная профессором Р. М. Робинсоном из Калифорнийского университета. Выбрав один из 12 пятиугольников, нужно построить пятиугольник, длина и ширина которого в три раза больше, чем у 9 из 11 оставшихся пятиугольников. Существует решение для каждого из 12 пентаминов, а не только для одного (от 15 решений для X до 497 для P). Существует вариант этой проблемы, когда исходная фигура сама по себе может быть использована для построения тройной фигуры. В этом случае число решений варьируется от 20 для X до 9144 для пентаминоидов P. Рисунок 7 Комментарии к презентации «Пентамино»В этой статье я предлагаю несколько задач с пентаминоидными фигурами, которые можно использовать как для первого обучения с этой головоломкой, так и для более подготовленных детей. Они подходят для начальной школы и для учащихся 5-7 классов (в зависимости от уровня подготовки учеников). Для проекта нам понадобится набор, состоящий из двенадцати блоков Пентамино. Их очень легко сделать самостоятельно в классе или дома. Нарисуйте фигуры на квадратном листе бумаги так, чтобы каждая состояла из пяти квадратов с длиной стороны 1 см. Затем наклейте квадратный лист на картон и вырежьте фигуры. Если хотите, можете раскрасить их мелками или маркерами. Пентамино готово. Презентация начинается с более простых задач. Из двенадцати фигур пентамино нужно отложить только те, которые будут использоваться для формирования данной конкретной картинки. Элементы презентации показываются щелчком мыши, чтобы их было легче найти. На следующем слайде показана картинка, которую вам нужно собрать. А на третьем слайде предлагается вариант ответа. Презентация содержит четыре таких задания, но при необходимости их количество всегда можно увеличить. Начиная с пятого задания, учащиеся должны выбрать фигуры, которые будут использованы для рисунка. В задании 5 требуется три пентаминоида для "маленькой собачки". В задании 6 дети должны не только собрать данные им картинки, но и попытаться объяснить, почему для этих задач может быть только одно решение. В задачах 7 и 8 может быть более одного решения, и можно устроить соревнование, кто первым найдет все возможные решения. Начиная с задачи 9 и далее, существует множество других решений. Невозможно найти все решения в классе. Эти задания могут быть предложены в качестве домашнего задания, или класс может быть разделен на группы. В задачах 13 и 14 используются все двенадцать пентаминоидов. Это довольно сложные задачи. Не все учащиеся 5-6 классов могут с ними справиться. Поэтому следует поощрять студентов, которые нашли решение этих проблем. Очень интересный результат получается, если предложить ученикам подумать о различных картинках, состоящих из пентаминоидов. Когда мы имеем дело с начальной школой, необходимо обеспечить одновременное использование не всех форм. В старших классах ученики могут использовать весь набор. В этом контексте следует помнить, что каждая форма встречается ровно один раз и что невозможно использовать деталь более одного раза. На самом деле, очень трудно охватить такой большой объем материала в одной презентации. Я предложил лишь малую часть того, что можно сделать с пентаминоидами. Заставьте его работать, и результат превзойдет ваши самые смелые ожидания. Ваши дети очень талантливы, и вам просто нужно направить их мысли в нужное русло. А потом...
Схемы и фигуры игры танграм
В последнее время танграм часто используется дизайнерами. Возможно, наиболее удачное применение танграма - в качестве предмета мебели. Есть столы для танграма, трансформируемая мягкая мебель и офисная мебель. Вся мебель tangram очень удобна и функциональна. Его можно менять в зависимости от настроения владельца. Сколько возможностей и комбинаций существует для треугольных, квадратных и прямоугольных полок? При покупке этой мебели вы получите инструкции и несколько листов карточек с различными темами, которые вы можете создать из этих полок. В гостиной можно поставить полки в форме людей, на таких же полках можно разместить кошек, кроликов и птиц в детской комнате, а в столовой или библиотеке - рисунок может быть на тему сооружений - домов, замков, храмов. Такой универсальный танграм.  Как извлечь корень из дроби - Примеры. Приклади Получите
 Стереометрия это часть геометрии которая изучает -
 Две прямые называются перпендикулярными если - Признак
 Что такое арифметический квадратный корень - Извлечение
 Прямоугольная система координат в пространстве - Описание
 Жан лерон д аламбер - Примечания править Стремление
 Множество это в математике - Счетные и несчетные множества
|
