Логарифм — свойства, формулы, график. Значениями а в y logax может быть.

В этом примере нет меньшего значения, поэтому ОДЕ для f(x) = log₃(x+4)+ log₃(8-x) является следующим интервалом (- ∞? 2лог₃6).

Калькулятор онлайн. Решение логарифмических уравнений.

Программа для решения логарифмического уравнения дает не только ответ на задачу, но и подробное решение с пояснениями, т.е. показывает процесс получения ответа.

Программа может быть полезна старшеклассникам для подготовки к экзаменам и тестам, а также для проверки знаний перед Единым государственным экзаменом. Он также может быть полезен родителям для проверки решения многих задач по математике и алгебре. Или вам слишком дорого нанимать репетитора или покупать новые книги? А может быть, вы просто хотите как можно быстрее выполнить домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробными решениями.

Таким образом, вы сможете научить себя и/или научить своих младших братьев и сестер и повысить уровень обучения решению проблем.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы. Правила ввода функций>>Почему решение на английском языке?>>С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами>>—>ln(b) или log(b) или log(e,b) — натуральный логарифм b log(10,b) — десятичный логарифм b log(a,b) — логарифм b, отнесенный к a

Введите логарифмическое уравнение Решите уравнение

Было обнаружено, что некоторые скрипты, необходимые для решения этой проблемы, не были загружены, и программа может не работать. Возможно, у вас включен AdBlock. Если да, отключите его и обновите страницу.

Поскольку так много людей заинтересованы в решении этой проблемы, ваш запрос был добавлен в очередь. Через несколько секунд решение будет показано ниже. Пожалуйста, подождите немного.

Игра «droneZone» —>3D модели Создание острова Эмулятор гравитации Игра «iChart» —>Головоломка SumWaves.

Немного теории.

Задача 1: Найти положительный корень уравнения x 4 = 81 Согласно определению арифметического корня, имеем \( x = \sqrt4 = 3 \).

Задача 2. Решите уравнение 3 x = 81 Запишем уравнение так: 3 x = 3 4, где x = 4.

В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том, что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3. Но уже, например, уравнение 3 x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень. Чтобы уметь решать такие уравнения, вводится понятие логарифма числа. Уравнение a x = b, где a>0, \( a \neq 1 \), b>0, имеет только один корень. Этот корень является логарифмом числа b по основанию a и обозначается log_ab, например, корень уравнения 3 x = 81 равен 4, т.е. log₃81 = 4.

Определение. Логарифмом положительного числа b по основанию a, где a>0, \( a

eq 1 \), это экспонента, на которую нужно увеличить a, чтобы получить b.₇Журнал

7 = 1, потому что 7 1 = 7

Это равенство справедливо при b>0, b>Определение логарифма можно записать следующим образом:

0, \( a

eq 1 \). Обычно его называют основным логарифмическим тождеством.₆₄Процесс нахождения логарифма числа называется логарифмированием. Процесс определения числа по его логарифму называется динамизацией.₆₄Рассчитать календарь₆₄128 Обозначим через log

128 = х. Согласно определению логарифма, 64 x = 128. Так как 64 = 2 6, 128 = 2 7, то 2 6x = 2 7, поэтому 6x = 7, x = 7/6. Ответ: log<-2\log_3 5>128 = 7/6

Вычислить \( 3^₃\Используя свойства силы и основное логарифмическое тождество, получаем следующий результат.

Десятичные и натуральные логарифмы

Решите уравнение log

(1-x) = 2 Согласно определению логарифма 3 2 = 1 — x при x = -8₁₀b

Для логарифмов чисел были созданы специальные таблицы (таблицы логарифмов). Логарифмы также можно вычислять с помощью микрокомпьютера. В обоих случаях находят только десятичные числа или натуральные логарифмы._eb

Определение. Десятичный логарифм числа — это логарифм этого числа по основанию 10, и вместо log пишется lg b.

Определение. Натуральный логарифм числа — это логарифм этого числа по основанию e, где e — иррациональное число, приближающееся к 2,7. В этом случае напишите ln b вместо log

Иррациональное число e играет важную роль в математике и ее приложениях. Число e можно представить в виде суммы: $ e = 1 + \frac + \frac + \frac + \frac + \dots + \frac + \dots $<\lg b><\lg a>Оказывается, что знание значений только десятичного или только натурального логарифма чисел достаточно для нахождения логарифмов чисел по любому основанию. Для этого используется формула для замены основания логарифма:<\ln b><\ln a>$

Графики логарифма

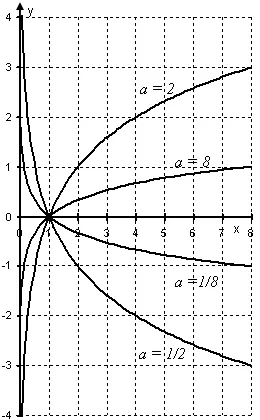
Эффекты формулы для замены основания логарифма. Для c = 10 и c = e выведена формула перехода к десятичной дроби и натуральному логарифму: $ \log_a b = \frac_ax для четырех значений основания логарифма : a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a>, \;\; \log_a b = \frac

Свойства логарифма

Область определения, множество значений, возрастание, убывание

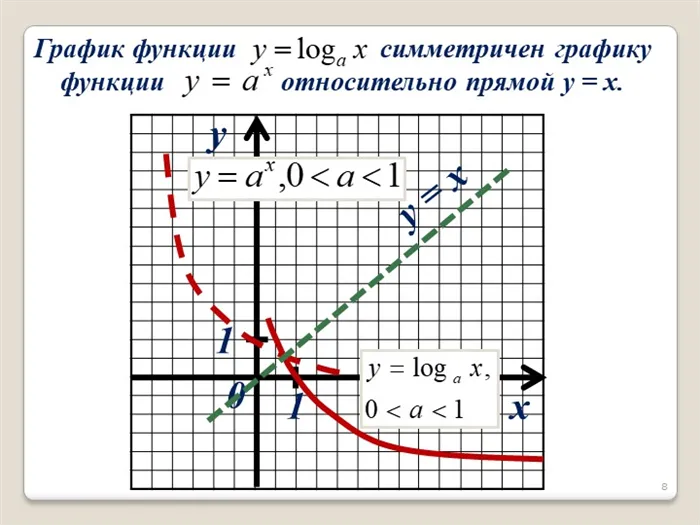
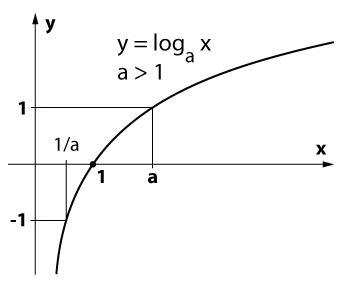
График логарифма получается при построении графика экспоненциальной функции путем зеркального отображения его на линии y = x. Графики функции y = log

1 Логарифм монотонно возрастает. При увеличении x рост значительно замедляется. В 0	0	0
Логарифм является монотонной функцией, т.е. не имеет экстремумов. Основные свойства логарифма перечислены в таблице.	– ∞	– ∞
Диапазон определения	Диапазон значений	Монотонность
Монотонно увеличивается	x = 1	x = 1
Монотонно уменьшается	Ноль, y = 0	Ноль, y = 0
+ ∞	– ∞
– ∞	+ ∞

Частные значения

нет

Основные формулы логарифмов

нет

Основное свойство логарифмов и его следствия

Формула замены основания

Логарифм по основанию 10 называется десятичным логарифмом и обозначается следующим образом: Логарифм по основанию e называется натуральным логарифмом:

Доказательство основных формул логарифмов

Свойства логарифма, вытекающие из определения обратной функции:

Логарифм — это математическая операция, при которой берется логарифм. В логарифме произведения коэффициентов преобразуются в суммы членов. Перечисление — это обратная математическая операция логарифма. При амплификации данное основание увеличивается до мощности выражения, на котором производится амплификация. Это преобразует суммы терминов в произведения факторов.

Формулы для логарифмов выводятся из формул для экспонент функций и из определения обратной функции.

Интеграл

Рассмотрим свойство функции экспоненты. Поэтому применим свойство экспоненциальной функции: .

Докажем формулу базового множества: ? Предполагая, что c = b, имеем:

Интеграл от логарифма вычисляется интегрированием по частям: Ну,

Логарифм, его свойства и график

Рассмотрим функцию комплексного числа z : Выразите комплексное число z через коэффициент r и аргумент φ: Используя свойства логарифма, получаем:. Однако аргумент φ не является однозначно определенным. Если задать, где n — целое число, то для разных n это будет одно и то же число.

Поэтому логарифм как функция комплексной переменной не является одномерной функцией.

• возрастание или убывание логарифма зависит от величины основания \(a\);
• оба графика проходят через точку \((1;0)\);
• оба графика ограничены слева осью \(OY:\ x\gt 0\).

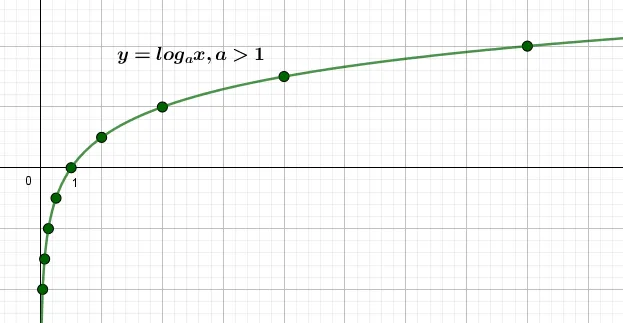
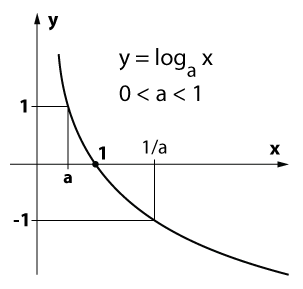
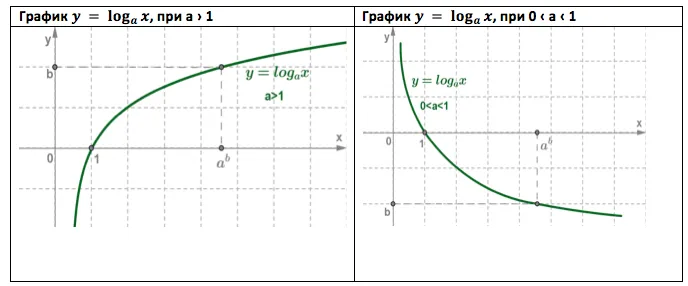
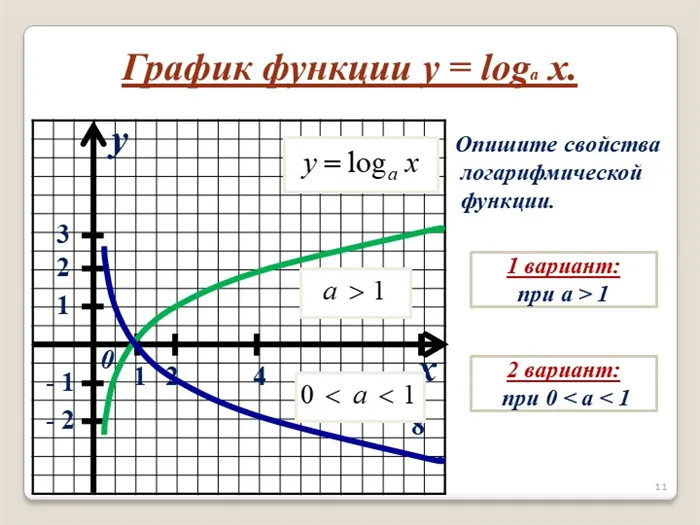
п.4 График и свойства логарифма при \(a\gt 1\)

п.1. Примеры

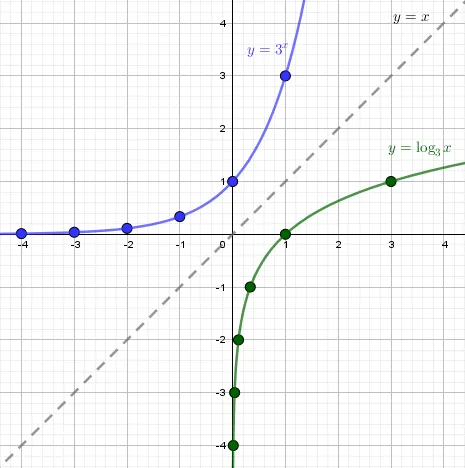
\begin \\\\\ y=\log_ax,\ a\gt 1 \end 1. область определения \(x\gt 0\) 2. область значений \(y\in\mathbb\) 3. \(y(1)=\log_a1=0\) — пересекает ось \(OX\) в точке (1;0) 4. функция возрастающая $ \log_aq\gt \log_as\Leftrightarrow q\gt s $ 5. At \(0\lt x\lt 1,\y\lt 0\) At \(x\gt 1,\y\gt 0\) At \(x

ightarrow +0,\y

ightarrow -\infty\) — не ограничено снизу At \(x

ightarrow +\infty,\y

ightarrow +\infty\) — не ограничено сверху 6. Функция непрерывна на всем своем интервале 7. Функция не является ни четной, ни нечетной

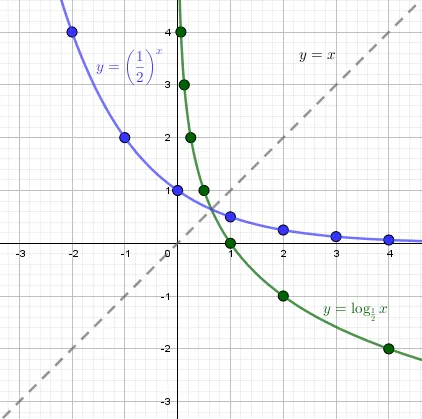
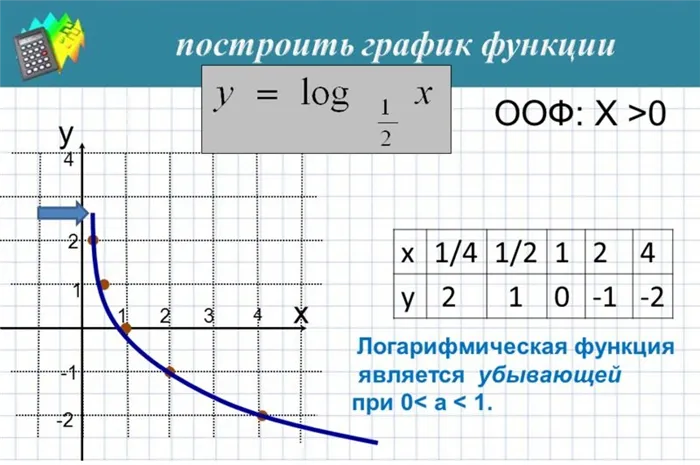
\begin \\\\\ y=\log_ax,\ 0\lt a\lt 1 \end 1. область определения \(x\gt 0\) 2. область значений \(y\in\mathbb\) 3. \(y(1)=\log_a1=0\) — пересекает ось \(OX\) в точке (1;0) 4. функция убывающая $ \log_aq\gt \log_as\Leftrightarrow q\lt s $ 5. At \(0\lt x\lt 1,\ y\gt 0\) At \(x\gt 1,\ y\lt 0\) At \(x

ightarrow +0,\ y

ightarrow +\infty\) — не ограничено сверху At \(x

Пример 4*. Постройте график функции: $ y=log_\left(\sqrt>-\sqrt\right) $ Упростим выражение в скобках: $ \sqrt>ightarrow +\infty,\ y<\left(1+\sqrt\right)^2>ightarrow -\infty\) — не ограничено снизу 6. Функция непрерывна на всем своем интервале 7. Функция не является ни четной, ни нечетной

«Обзор традиционных и современных методик для формирования навыков арифметических вычислений в уме у младших школьников»

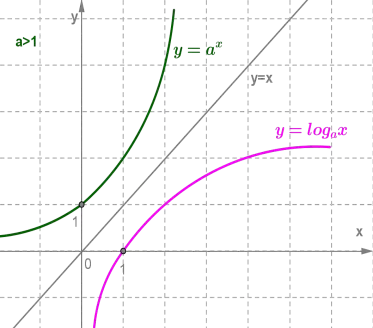
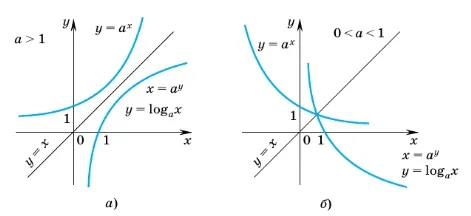
Пример 1: Постройте графики функций в одной системе координат. Сделайте выводы. a) \(y=3^x,\(y=\log_3x\) Экспоненциальная функция \(y=3^x\) и логарифм \(y=\log_3x\) симметричны относительно \(y=x\). Эти функции являются обратными друг другу (см. §2 учебника для 9 класса). Функции не пересекаются.

b) \(y=\left(\frac12

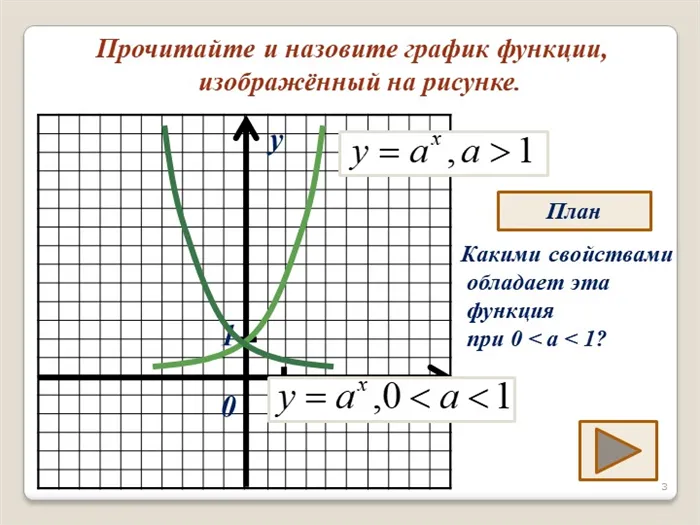
ight)^x,\ y=\log_x\) Экспоненциальная функция \(y=\left(\frac12

ight)^x\) и логарифм \(y=\log_x\) симметричны относительно оси \(y=\x\). Эти функции являются инверсиями друг друга. Функции перекрываются.

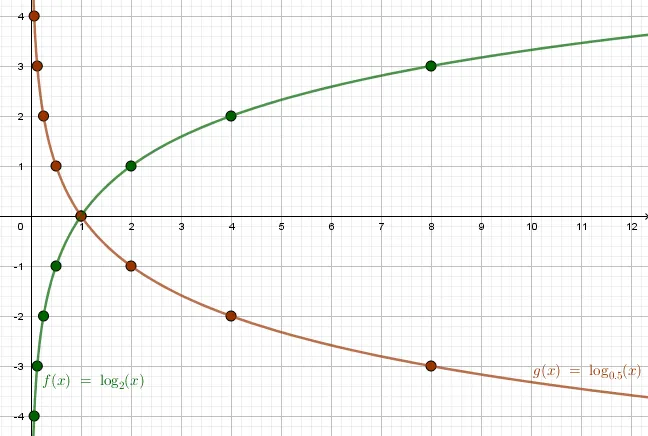
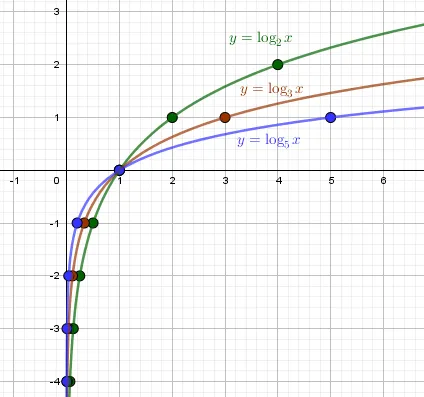
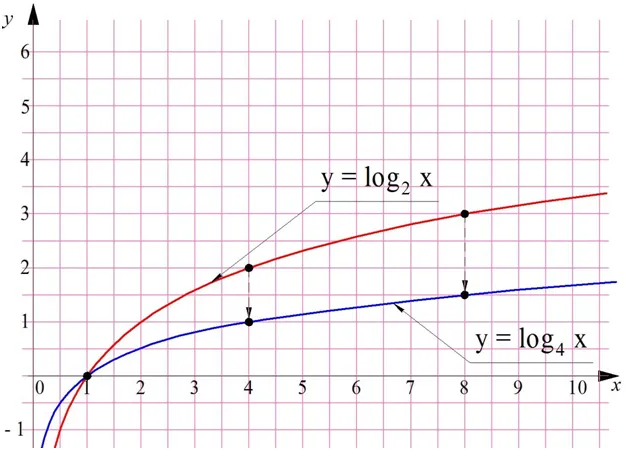
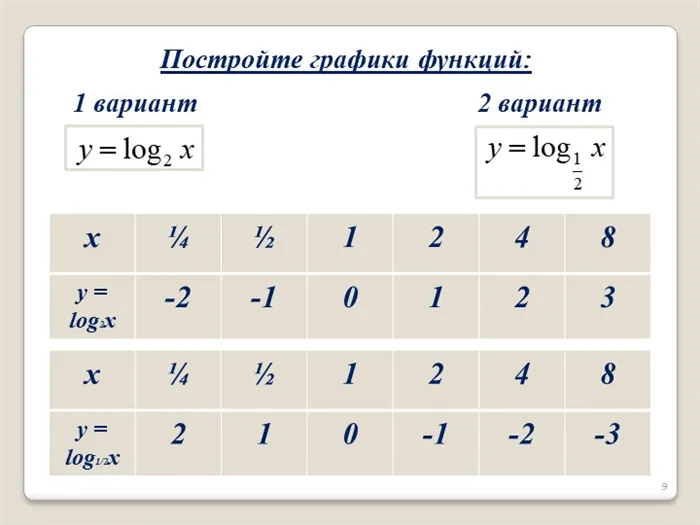
c) \(y=\log_2x,\y=\log_3x,\y=\log_5x\) В \(a\gt 1\) все логарифмы являются возрастающими функциями. Все графики пересекают ось \(OX\) в точке (1;0). Чем больше \(a\), тем медленнее функция падает к \(-\infty\) по мере приближения к \(x\стрелка вправо +0\), и тем медленнее функция стремится к \(+\infty\) при \(x\стрелка вправо +\infty\).

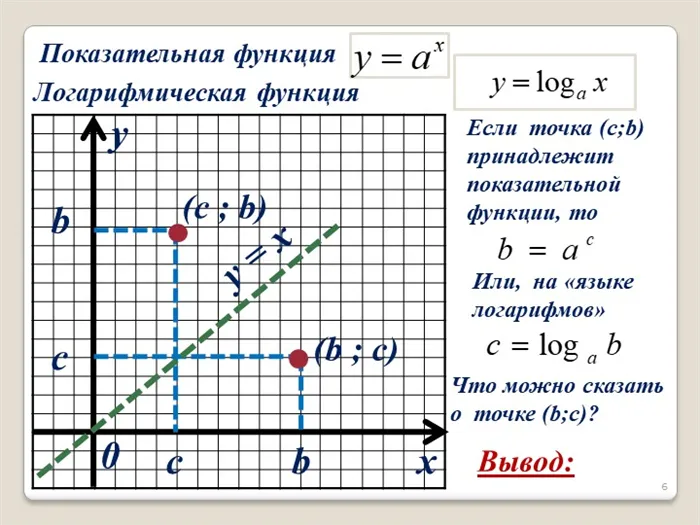
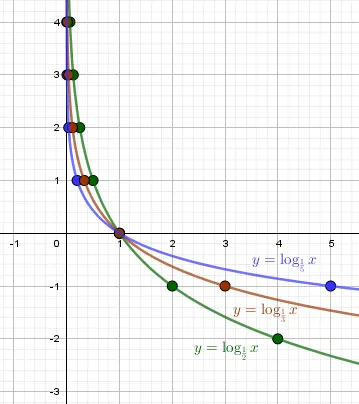
г) \(y=\log_x,\ y=\log_x,\ y=\log_x\) В \(0\lt a\lt 1\) все логарифмы являются убывающими функциями. Все графики пересекают ось \(OX\) в точке (1;0). Чем меньше \(a\), тем медленнее функция поднимается в направлении \(+\infty\) по мере приближения к \(x\стрелка вправо +0\); аналогично, функция медленнее наклоняется в направлении \(-\infty\) при \(x\стрелка вправо +\infty\).

Три основных вида логарифмов

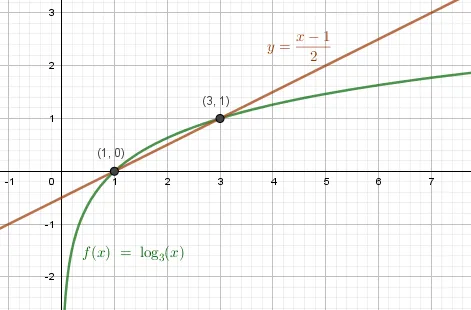
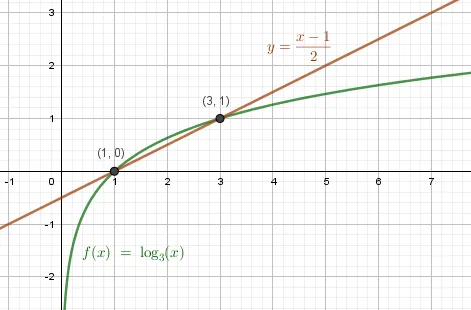
Пример 2. Решите уравнение графически: a) \(\log_3x=\frac\) Ответ.

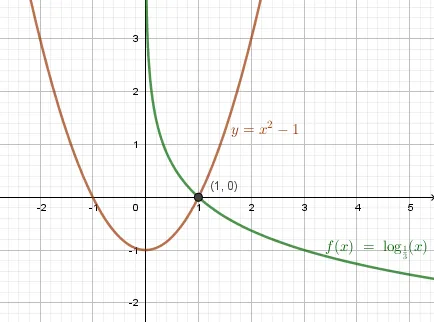
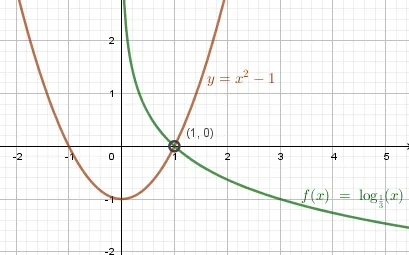
b) \(\log_x=x^2-1\) Ответ: \(x=1\)

Пример 3. Решите неравенства графически: a) \(\log_3x\leq\frac\) ОДЗ логарифма \(x\gt 0\) Кривая логарифма лежит ниже прямой линии и пересекает ее через определенные промежутки времени: \(0\lt x\leq 1\cup x\geq 3\) Мы включаем пересечения, потому что неравенство не является строгим. Ответ.₂б) \(\log_x\gt x^2-1\) ОДЗ логарифма \(x\gt 0\) Кривая логарифма лежит выше прямой в интервале \(0\lt x\lt 1\). Мы опускаем перехват, поскольку неравенство является строгим. Ответ.

-\sqrt=\sqrt=\sqrt

-\sqrt=1+\sqrt-\sqrt=1 $ Имеем: \bginning y=log_1\leftarrow \beginning y=0\ cos2x\gt 0\ cos2x

Преобразования логарифмических выражений

e 1\end \ cos2x\gt 0

ightarrow-\frac\pi2+2\pi n\lt 2x\lt\frac\pi2+2\pi n

ightarrow-… \\\frac\pi4+\pi n\lt x\ltfrac\pi4+\pi n\ cos2x

e 1\Rightarrow 2x

e 2\pi n\Rightarrow x

e\pi n \end функция: \( \начало y=0\ -\frac\pi4+\pi n\lt x\lt\frac\pi4+\pi n,\ x

e\pi n \конец \).

eq 1 \), это экспонента, на которую нужно увеличить a, чтобы получить b.₂2 слайда Дата рождения: 1550 Место рождения: замок Мерчистон, тогдашний пригород Эдинбурга Дата смерти: 4 апреля 1617 Место смерти: Эдинбург Научная область: математика Альма-матер: Университет Сент-Эндрюса Известен как: Джон Напьер 2 Изобретатель логарифма.

eq 1 \), это экспонента, на которую нужно увеличить a, чтобы получить b.₂4 Слайд 1) D(f) — область определения функции. 2) Аппроксимация или избыточность функции. 4) Ограниченность функции. 5) Высшие и низшие значения функции. 6) Непрерывность функции. 7) E(f) — это диапазон значений функции. 3) Интервалы нарастания и спада функции. 8) Выпуклость функции. Графическая схема чтения: 4

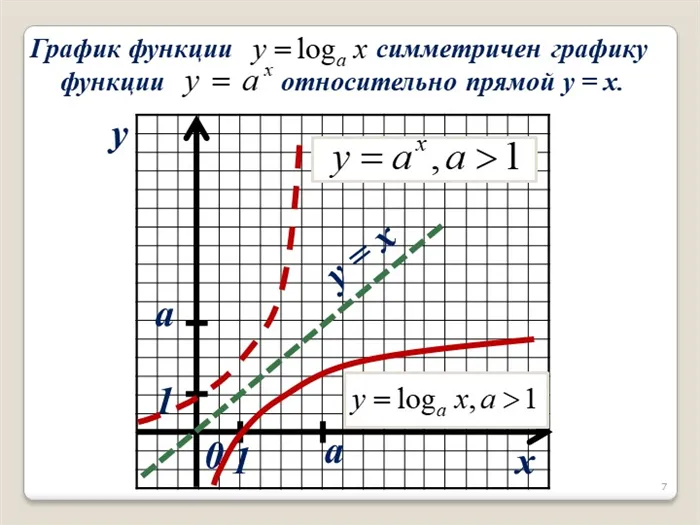
eq 1 \), это экспонента, на которую нужно увеличить a, чтобы получить b.₂6 Слайд x y 0 c b c b y = x Экспоненциальная функция Логарифмическая функция (c ; b) Если точка (c;b) принадлежит экспоненциальной функции, то ИЛИ, говоря «логарифмическим языком» Что можно сказать о точке (b;c)?

В математике логарифмы изучаются с произвольными положительными основаниями. На практике, однако, наиболее распространены три из этих типов.

Первый — десятичный логарифм, основание которого равно 10. Дело в том, что до изобретения калькуляторов и компьютеров вы могли быстро и точно перемножать большие числа с помощью такого устройства, как логарифмическая линейка. История понятия логарифма начинается в 16 и 17 веках, когда возникла необходимость выполнять сложные арифметические операции с большими числами. Специальный символ lg используется для обозначения десятичных логарифмов, т.е. десятичного номера числа.

В связи с развитием электроники десятичные логарифмы сегодня используются гораздо реже, чем в 50-60 годах 20 века. Однако, поскольку почти вся компьютерная технология основана на двоичной системе счисления, двоичный логарифм log

b. Для его обозначения не используются специальные символы, но он особенно часто используется в информатике и при оценке сложности алгоритмов.

Наконец, самый важный логарифм — натуральный логарифм. Это логарифм, основанием которого является число e, которое приблизительно равно 2,71828…. Он обозначается символом ln, т.е.

Свойства натурального логарифма, отличающие его от других логарифмов, будут изучены позже в 11 классе. Обратите внимание, что многие натуральные формулы включают натуральный логарифм.

Чтобы работать с логарифмическими выражениями, нам необходимо знать некоторые основные свойства логарифмов. Первый из них помогает вычислить логарифм произведения.

Чтобы доказать это правило, введем обозначения. Допустим.

Затем нужно доказать, что z = x + y. Из определения логарифма мы можем записать

Теперь подставьте (1) и (2) в (3):

Отсюда следует, что a z = a x + y. В этом равенстве в обеих частях имеются степени одного и того же основания a. Это означает, что их степени также должны совпадать, т.е. их степени также должны совпадать.

что мы и пытались доказать.

Докажем это правило на простом примере. Очевидно, что

Протокол

4 = 2, потому что 2 2 = 4

Протокол

8 = 3, потому что 2 3 = 8

Протокол

Переход к новому основанию алгоритма

32 = 5, потому что 2 5 = 32

С одной стороны, потому что

С другой стороны, 32 можно представить как произведение 4-8, т.е.

Принимая это во внимание, следует, что

Давайте покажем несколько примеров применения правила, которое мы только что доказали:

Независимо от этого, следует отметить, что правило сложения логарифмов действует и в том случае, когда складываются не два, а несколько логарифмов:

Второе правило используется для определения логарифма степени числа.

В общем случае экспонента может быть взята и записана перед знаком логарифма. Для ясности сначала приводится доказательство только для случая, когда r — целая степень. Тогда число b r можно представить как произведение r множителей, равных b. Однако логарифм такого произведения можно заменить суммой r логарифмов:₂₅Однако более строгое доказательство должно учитывать и случай, когда r — отрицательное или даже дробное число. Итак, как и при доказательстве первого правила, введем переменные. Пусть

Получается, что мы должны доказать, что y = r-x. Следующие формулы следуют из определения логарифма:

Подставляя первую формулу во вторую, получаем:₄Опять же, если две равные силы имеют равные основания, то экспоненты обязательно равны:

Это и есть то равенство, которое мы пытались доказать.₄Мы хотим показать, как работает это свойство логарифмов:₂Это правило действует и в обратном направлении:

Задание. Чему равна дробь_aТретье правило помогает вычислить логарифм дроби или класса._bЧтобы доказать это свойство логарифмов, мы используем два правила, которые мы уже доказали. Во-первых, вспомните, что любое число c в степени (- 1) является дробью 1/s:

Тогда доказательство записывается в две строки:

До сих пор мы рассматривали преобразования, при которых основание логарифма не меняется. Однако иногда необходимо сложить или вычесть логарифмы с разными основаниями. Предположим, нам нужно вычислить значение выражения_сПоскольку основания двух логарифмов различны, мы не можем использовать формулу, которую вывели для разницы между логарифмами. Однако мы можем попытаться привести один из логарифмов к новому основанию. Существует специальная формула для такой операции._aДавайте докажем это утверждение. Для этого мы вводим новые переменные:_cПосле определения логарифма мы можем написать уравнения._сСледовательно, a x = c y. Замените a на c z в этом уравнении и получите:_aОтсюда следует, что zx = y, или x = y/z. Теперь подставьте логарифмы для x, y и z, и вы получите тождество, которое нам нужно доказать:_cВернемся к примеру

Теперь мы можем выполнить эти вычисления, но для этого нам сначала нужно использовать логарифм_a9 к базе 5:

Теперь мы можем рассчитать, какова искомая разница:_aФормула для перевода в новое основание позволяет по-другому взглянуть на графики логарифмических функций. Пусть функция y =log_1/аx. Попробуем свести его к экспоненте 2:

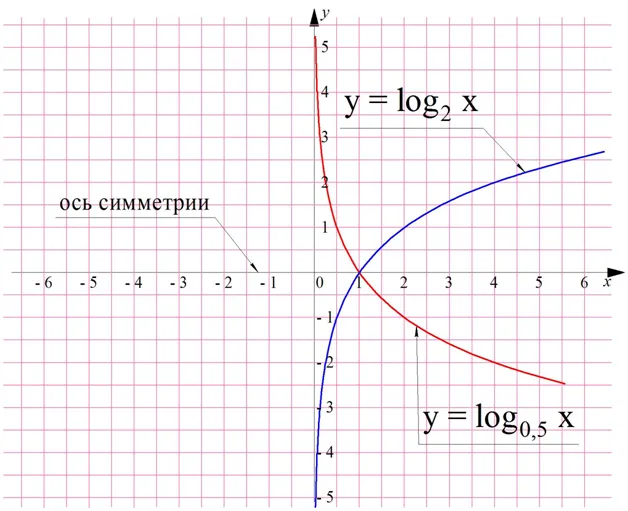
Оказывается, что график y = log