При работе с сегментами можно выполнять различные арифметические операции на основе их свойств. Математические правила для определения положения общего вектора называются линейными правилами. Различают следующие операции над разграниченными строками:
Векторы: основные понятия. Координаты вектора. Длина вектора
Тот факт, что вектор — это направленный отрезок, будет легче понять, если мы рассмотрим различия между скалярными и векторными величинами.
В следующей таблице «не-векторы» — это скалярные величины или простые скаляры, а «векторы» — векторные величины.
| Невекторы | Организации |
| Масса | Гравитация |
| Длина | Маршрут |
| Время | Ускорение |
| Плотность | Давление |
| Температура | Скорость |
| Группа | |
| Регион | |
| Векторная единица |
Векторы (скаляры) не имеют направления, а векторы имеют направление.
Вектор обязательно проходит из точки A по прямой в точку B. Численное значение вектора — это длина, а физическое и геометрическое значение — направление. Отсюда следует первое, более простое определение вектора. Таким образом, вектор — это направленный отрезок, ведущий из точки A в точку B и обозначаемый через .
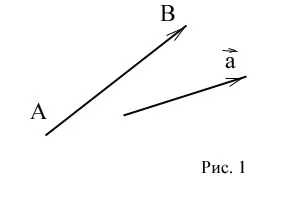
И чтобы начать различные операции с векторами, нам необходимо ознакомиться с еще одним определением вектора.
Вектор — это способ представления точки, которую можно достичь из определенной начальной точки. Например, трехмерный вектор обычно записывается в виде ( x, y, z ). Проще говоря, эти цифры показывают, какое расстояние нужно проехать в трех разных направлениях, чтобы достичь точки.
Давайте зададим вектор. В данном случае x = 3 (правая рука указывает вправо), y = 1 (левая рука указывает вперед), z = 5 (под точкой находится лестница, ведущая вверх). Соответственно, вы находите точку, пройдя 3 метра в направлении, на которое указывает ваша правая рука, затем 1 метр в направлении, на которое указывает ваша левая рука, затем поднимаетесь по лестнице и 5 метров до конечной точки.
Все остальные термины являются уточнениями вышеприведенного объяснения, необходимыми для различных операций с векторами, то есть для решения практических задач. Давайте рассмотрим эти более строгие определения, остановившись на формальных векторных задачах.
Физическими примерами векторных величин являются смещение материальной точки, перемещающейся в пространстве, скорость и ускорение этой точки, а также сила, действующая на нее.
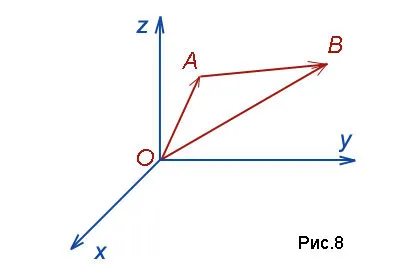
Геометрический вектор представлен в двух- и трехмерном пространстве в виде направленной линии. Это раздел с началом и концом.
Если A — начало, а B — конец вектора, то вектор обозначается символом или простой строчной буквой. На рисунке конец вектора обозначается стрелкой (рис. 1).
Длина (или единица) геометрического вектора — это длина отрезка, который его создает.
Два вектора считаются равными, если они могут быть выровнены путем параллельной передачи (если их направления совпадают), т.е. если они параллельны, направлены в одну сторону и имеют одинаковую длину.
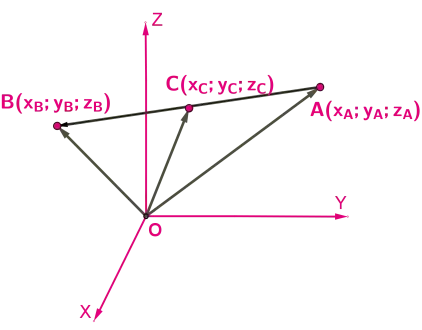
В физике часто рассматривают фиксированные векторы, заданные точкой атаки, длиной и направлением. Если точка атаки вектора не имеет значения, его можно переместить в любую точку пространства, сохранив при этом его длину и направление. В этом случае вектор называется свободным вектором. В высшей математике векторы изучаются в области аналитической геометрии, где рассматриваются свободные векторы. Итак, если свободный вектор — это вектор, начало которого может находиться в любой точке пространства, то все векторы с одинаковым направлением и длиной считаются одинаковыми.
Координаты вектора в прямоугольной декартовой системой координат в пространстве
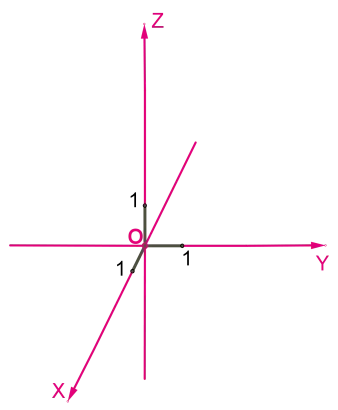
В упорядоченной системе координат 0xyz ось Ox называется осью абсцисс, ось 0y — осью ординат, а ось 0z — осью аппликат.
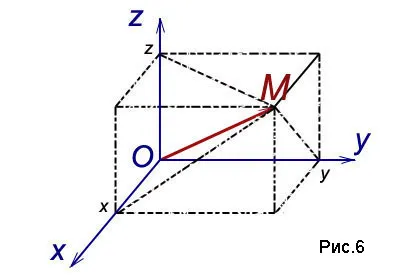
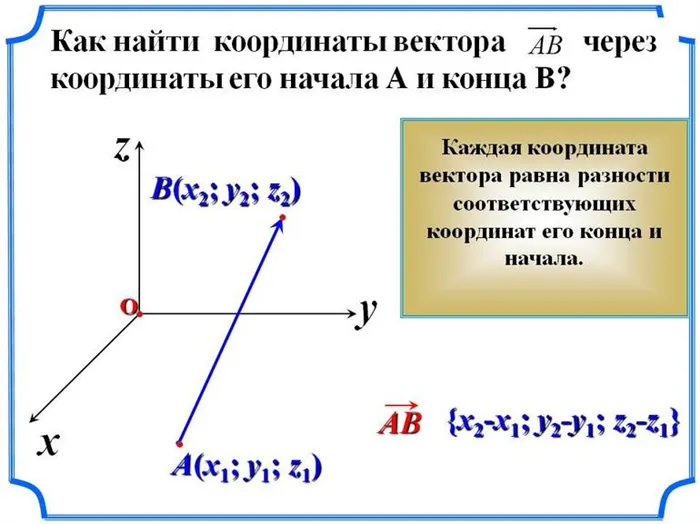
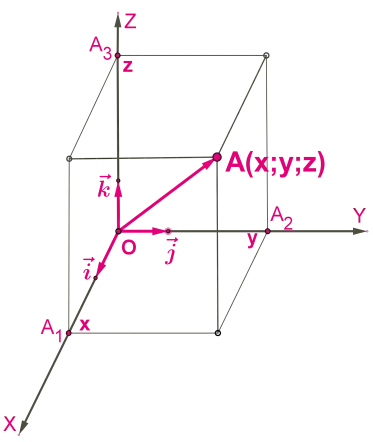
Каждой точке M в пространстве мы присваиваем вектор
радиус-вектор точки M и спроецировать его на каждую из координатных осей. Обозначим значения соответствующих проекций:
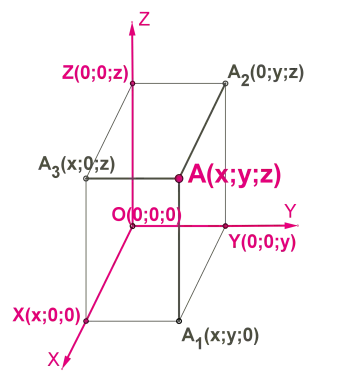
Числа x, y, z называются координатами точки M, то есть абсциссой, ординатой и апликой, и записываются как упорядоченные точечные числа: M (x; y; z) (рис. 6).
Вектор единичной длины, направление которого совпадает с направлением оси, называется единичным вектором (или ортогональным вектором) оси. Обозначим через
Аналогично, порядки координатных осей: Ox, Oy, Oz
Теорема. Каждый вектор может быть проанализирован в терминах координатных осей:
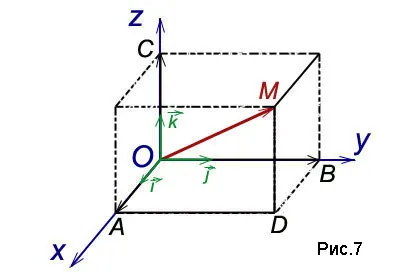
Уравнение (2) называется разложением вектора по координатным осям. Коэффициенты этого разложения являются проекциями вектора на координатные оси. Поэтому коэффициенты разложения (2) вектора по координатным осям являются координатами вектора.
Поскольку вектор и тройка его координат однозначно определены в пространстве, вектор можно записать в следующей форме.
Векторные представления формы (2) и (3) идентичны.
Условие коллинеарности векторов в координатах
Векторы считаются коллинеарными, если они связаны следующим соотношением.
Пусть векторы будут. Эти векторы коллинеарны, если координаты векторов связаны друг с другом следующим образом.
то есть координаты векторов пропорциональны.
Пример 1. Коллинеарны ли эти векторы?
Решение. Найдите отношение координат данных векторов:
Координаты векторов пропорциональны, то есть векторы коллинеарны или, что одно и то же, параллельны.
Координатные векторы
Векторыi → и j →называются координатными векторами для данной системы координат.
Мы выводим любой вектор a → из начала координат. Согласно геометрическому определению операций над векторами, вектор a → можно представить в виде a → = a x — i → + a y — j →, где коэффициентами являютсяa xиa y— уникальны, их уникальность можно легко доказать обратным методом.
Разложение вектора
Разложение вектораa →с векторами координатi → и j →в плоскостиэто представление вида a → = a x — i → + a y — j → .
Коэффициенты a x и a yназываются координатами вектора в данной системе координат на плоскости.
Координаты вектора в этой системе координат принято записывать в скобках через запятую, при этом заданные координаты отделяются от векторного обозначения знаком равенства. Например, обозначение a → = ( 2 ; — 3 ) означает, что вектор a → в данной системе координат имеет координаты ( 2 ; — 3 ) и может быть представлен как продолжение координатных векторов i → и j → в виде a → = 2 — i → — 3 — j →.
Обратите внимание, что порядок записи координат важен; если вы запишите координаты вектора в другом порядке, вы получите совершенно другой вектор.
Из определений координат векторов и их анализа следует, что единичные векторы i → и j → имеют координаты ( 1 ; 0 ) и ( 0 ; 1 ) соответственно, и могут быть представлены в виде i → = 1 — i → + 0 — j → ; j → = 0 — i → + 1 — j → .
Существует также нулевой вектор 0 → с координатами ( 0 ; 0 ) и разложением 0 → = 0 — i → + 0 — j → .
Равные и противоположные векторы
Векторы a → и b → равныесли их соответствующие координаты равны.
Противоположный векторэто вектор, противоположный данному вектору.
Из этого следует, что координаты такого вектора противоположны координатам этого вектора, т.е. — a → = ( — a x ; — a y ) .
Для прямоугольной системы координат в трехмерном пространстве приведенные выше утверждения могут быть определены аналогичным образом. В такой системе координат есть три координатных вектора i →, j →, k →, и любой вектор a → расширяется не по двум, а по трем координатам и имеет вид a → = a x — i → + a y — j → + a z — k →, а коэффициенты этого расширения ( a x ; a y ; a z ) называютсякоординаты вектора в заданной (трехмерной) системе координат.
Поэтому векторы координат в трехмерном пространстве также принимают значение 1 и имеют координаты i → = ( 1 ; 0 ; 0 ; 0 ), j → = ( 0 ; 1 ; 0 ), k → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0 ; 1 ), координаты нулевого вектора также нулевые 0 → = ( 0 ; 0, 0, 0 ), и в этом случае два вектора считаются равными, если все три соответствующие координаты вектора между ними равны a → = b → ⇔ a x = b x, a y = b y, a z = b z, а координаты противоположного вектора a → противоположны соответствующим координатам вектора a →, т.е. т.е. — a → = ( — a x ; — a y ; — a z ) .
Координаты векторов
Из уроков алгебры мы знаем прямоугольную систему координат. Она имеет оси O и O, и каждая точка, отмеченная на плоскости, имеет свои координаты:

Конечно, мы также можем отмечать векторы в координатной плоскости. Построим два вектора, которые начинаются в начале координат, имеют длину 1 и направления которых соответствуют направлениям координатных осей. Вектор на оси О обозначается i, а вектор на оси О — j.
Эти векторы называются единичными векторами или ортонами (также используется термин координатный вектор). Они неколлинеарны, что означает, что любой вектор на плоскости может быть разложен на единичные векторы. Коэффициенты такого разложения — это просто координаты вектора.

Давайте на примере найдем координаты вектора. Предположим, у нас есть вектор a :

Нам нужно разложить a на векторы i и j. Для этого нам нужно посмотреть на него с определенной точки. Удобно переместить вектор a в начало координат:
Теперь нужно провести прямые, параллельные векторам i и j через конец a. В результате получится прямоугольник ABCD:

Мы можем записать равенство:

Поэтому координатами этого вектора являются числа 3 и 2. Он записывается следующим образом:
Обратите внимание, что порядок цифр в скобках имеет существенное значение. Первое число — это коэффициент разложения перед вектором i. Эту координату можно назвать координатой x (по аналогии с координатами точки). Второе число — это коэффициент вектора j, который является координатой y. Отметим также очевидный факт, что координаты равных векторов одинаковы.
В приведенном примере легко видеть, что после перемещения вектора в начало координат, координаты его конца (обозначенного C) совпадают с координатами самого вектора. Точка C имеет координаты (3; 2).
Это несколько упрощает определение координат вектора. Достаточно переместить вектор из начальной точки, а затем исследовать координаты его конечной точки. Обратите внимание, что вектор, начало которого совпадает с началом координат, имеет специальное название — радиус-вектор.

Задача. Найдите координаты векторов a, b, c и d на рисунке:
Сложение и вычитание векторов
Предположим, что у нас есть векторы a 1; у1>Предположим, у нас есть векторы a и b 2; у2>. Зная только их координаты, можете ли вы определить их сумму и разность? Оказывается, можно. Согласно определению координат вектора (мы помним, что это коэффициенты разложения вектора по оригиналам), мы действительно можем написать:

Это обозначение означает, что c имеет координаты 1+ х2; у1+ у2>. В результате мы можем сформулировать правило сложения векторов:
Поясним это правило на примере. Добавим векторы a и b. Понятно, что в результате получается новый вектор, который мы обозначим через c. Чтобы найти его первую координату, мы складываем первые координаты векторов a и b :
Чтобы найти его вторую координату, мы складываем вторые координаты соответствующих векторов:
В результате получается вектор с .
Задача. Добавьте векторы, имеющие координаты:
Решение. Сначала просто сложите простые числа в скобках (и получите координату x ), затем сложите вторые числа (и получите координату y ):
Теперь давайте попробуем понять, как вычисляется разница между двумя векторами. Предположим, что у нас есть векторы с заданными координатами a 1; у1>Предположим, у нас есть векторы a и b 2; у2>. Давайте снова запишем их эволюцию в единичных векторах:

Теперь мы можем сформулировать правило для вычитания векторов:
Например, вычтем вектор b из вектора a. Искомая разность — это вектор, координата x которого равна разности простых координат векторов a и b:
Аналогично вычисляем координату y:
В результате мы имеем вектор с координатами .
Задача. Вычтите вектор b из вектора a, если их координаты известны:
Решение. Во всех случаях сначала вычтите первую координату вектора a из первой координаты вектора b, чтобы получить координату x искомого вектора. Затем повторите операцию со второй координатой (т.е. y):

Теперь рассмотрим такую операцию, как умножение вектора на число. Опять же, вектор a с координатами x1и y1можно разложить на коэффициенты следующим образом:
Признак коллинеарности векторов
Напомним, что если два вектора (назовем их a и b) коллинеарны, то обязательно существует число k такое, что

Из равенства (1) и правила умножения вектора на число, описанного выше, вытекают два соотношения между этими координатами:
Если числа x2и y2не равны нулю, то из каждого уравнения можно выразить число k, тогда выражения можно приравнять:
Получаем соотношение, которое можно считать свойством коллинеарных векторов. Это правило работает и в обратном направлении — если координаты векторов удовлетворяют производной, то можно смело утверждать, что векторы слиплись.
Примечание. Фраза «тогда и только тогда» означает, что правило работает в обе стороны — из пропорциональности координат следует конгруэнтность векторов, а из конгруэнтности векторов следует пропорциональность координат.
Мы покажем, как использовать этот символ для коллинеарности векторов. Предположим, что вектор a имеет координаты, а вектор b имеет координаты. Нам нужно определить, являются ли они коллинеарными. Для этого мы делим координаты x друг на друга:
Получаем число 3. Затем также делим координату y:
Снова получаем 3. Тот факт, что в обоих случаях мы получаем одно и то же число, говорит о том, что векторы коллинеарны. Кроме того, мы можем написать, что вектор b в три раза больше a:
В данном примере мы разделили координаты второго вектора b на координаты первого вектора a. Но можно разделить координаты a на координаты b и наоборот:
Конечно, мы все равно получим то же число.
Особый случай — когда одна из координат вектора равна нулю. Например, предположим, что вектор имеет координаты 1>и y1≠ 0. Любой вектор, прилипший к нему, может быть определен умножением вектора на число k. В этом случае координаты 2; у2>являются:
Оказывается, что координата x коллинеарного вектора также обязательно равна нулю. Координаты y, в свою очередь2и y1может быть произвольным, так как мы всегда можем найти число k, для которого выполняется условие
Например, если у нас есть вектор с, то можно сказать, что он коллинеарен с любым вектором, первая координата которого также равна нулю,
Но любой вектор, чья x-координата НЕ равна нулю, НЕ коллинеарен с. В частности, он не является коллинеарным с вектором:
Та же логика применима, если не x-координата, а y-координата равна нулю.
Если обе координаты вектора равны нулю, то это нулевой вектор, т.е. точка. Следует помнить, что такой вектор коллинеарен с любым другим вектором.
Задание. Определите, являются ли два вектора коллинеарными, если их координаты равны:








