Наименее любимый экзаменационный блок у большинства студентов — это геометрия, потому что он трудный. Некоторые вообще не понимают этого. А в геометрии есть самый нелюбимый вид работы — задачи на доказательство. Почему это так и как мы можем помочь студентам решить их?
Геометрия на ЕГЭ по математике: как решать, если не понимаешь
Студенты, для которых геометрия является чем-то страшным на экзаменах A-level, часто испытывают трудности в изучении предмета и получают посредственные оценки. Вместо этого вы можете просто изменить свою подготовку. В этой статье вы узнаете, какие книги использовать для изучения теории, где решать задачи и как правильно оформлять ответы.
То, какие книги вы используете для подготовки к ЕГЭ, имеет решающее значение. Геометрия могла быть легкой в 2020 году, но что в этом хорошего, если в 2021 году все изменилось?
Иногда бывает так, что студенту приходится десять раз прочитать страницу теории, чтобы понять хотя бы одно слово. В другом учебнике эта информация укладывается в две строки и объясняется так, чтобы ее было легче понять.
Вот учебники, по которым можно легко решить геометрию в США:
- Шарыгин И.Ф. «Наглядная геометрия»;
- Золотарева Н.Д. «Геометрия. Базовый курс с решениями и указаниями»;
- Золотарева Н.Д. «Геометрия. Углубленный курс с решениями и указаниями»;
- Акопян А.В. «Геометрия в картинках».
Некоторые из них простым языком объясняют, почему геометрия так сложна на ЕГЭ. Книга Акопяна, напротив, предназначена для людей с опытом — в ней нет ни одного слова (кроме названий), только рисунки.

Что и где решать?
После изучения теории вам необходимо углубить материал, решая задачи. Где можно сделать это так, чтобы геометрия не казалась страшной в США? Давайте узнаем.
- РешуЕГЭ. Этот сервис можно использовать для отработки своих знаний, так как на нем удобно выбирать конкретные задачи для закрепления и составлять свой собственный вариант. Однако, на нем можно встретить задания с ошибками, версии задач прошлого года, поэтому нужно тщательно фильтровать все, что попадается там. Если не хотите тратить на это время, а сосредоточиться на ЕГЭ — геометрия есть и на других сервисах.
- Открытый банк заданий ФИПИ. На сайте официального составителя ЕГЭ геометрия не покажется сложной. А еще можно не волноваться за ошибки в заданиях.
- Незнайка. Это сайт для отработки всех предметов на ЕГЭ. Геометрия тоже там есть. На сайте собрано много вариантов для решения любого предмета — нужно просто выбрать, что необходимо подтянуть. Теории там нет, но есть возможность посмотреть решение задач других пользователей и почерпнуть для себя что-то новое.
- Варианты Алекса Ларина. Про них и говорить не нужно — они сложные, но после них на ЕГЭ геометрия будет решаться на «ура».
Кроме того, необходимо научиться правильно формулировать ответы. Об этом мы поговорим ниже.
Как правильно оформлять ответы
Представьте, что вы объясняете человеку, который совсем не знает предмета, почему геометрия так сложна в ЕГЭ. Вы описываете каждое действие так, чтобы они могли понять последовательность и увидеть общую нить их размышлений. Это относится и ко мне.
Должен быть набросок:
- Четким;
- Структурированным;
- Понятным;
- Развернутым.
Это не означает, что эксперты не понимают предмет. Напротив, им нужно знать, что вы не ошиблись с геометрией в США. И всегда стоит помнить, что не все, что очевидно для вас, очевидно для всех остальных. Кстати, не только во время экзамена.
Распространенная причина страха
Именно учитель формирует 90 процентов отношения к предмету. Если ему удастся вызвать интерес у детей, то даже самые трудные третьеклассники заинтересуются геометрией. Дети будут готовы остаться в классе на перемене только для того, чтобы увидеть другой вариант решения проблемы.
С другой стороны, если тема объясняется скучным, непонятным способом, ее становится трудно понять. В таких случаях рекомендуется следовать приведенным ниже советам.
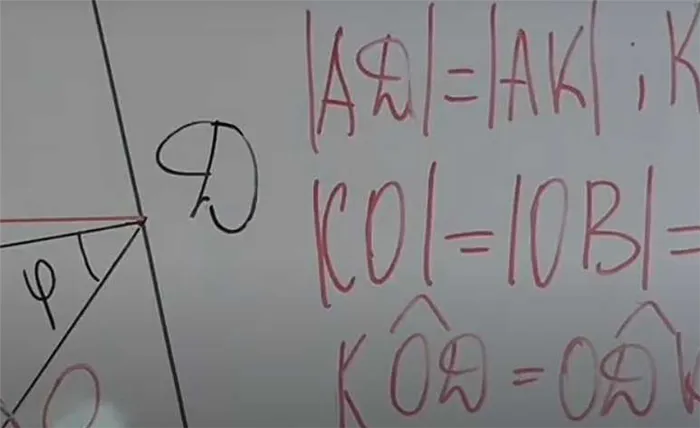
С чего начать изучение
Прежде чем углубиться в тему, следует понять, что ничего нельзя сделать за один день. Процесс обучения займет некоторое время. Точный срок зависит от поставленной цели. Если цель — только получить хорошую оценку на экзамене или написать контрольную, достаточно выучить определенную тему и немного попрактиковаться.
Прочитайте последние несколько абзацев в своем учебнике. Не нужно торопиться, постарайтесь осмыслить написанное. Затем попробуйте решить некоторые проблемы. Постоянно возвращайтесь к тексту учебника и пытайтесь самостоятельно «увидеть» алгоритм решения задачи.
Если поначалу у вас возникнут трудности, это нормально. Главное — не сдаваться и упорствовать. Посмотрите опубликованную версию руководства, справочник, но не просто копируйте готовые решения, постарайтесь понять логику алгоритма. Если подобная проблема обсуждалась в классе, постарайтесь вспомнить, что говорил о ней учитель. Возможно, кое-что из того, что он сказал, будет вам полезно.
Не пренебрегайте помощью своих сверстников. Иногда одноклассники, друзья, братья или сестры могут донести мысль гораздо быстрее, чем взрослый.

Другое дело, когда перед студентом стоит задача углубиться в предмет. Требуется гораздо больше усилий, и опять же, мотивация и осознание того, что работа должна быть сделана, имеют первостепенное значение. Помните. Решение проблемы в одиночку и систематическое копирование готовых решений из Интернета вам не помогут. Чтобы решить ее, необходимо систематически и достаточно часто практиковаться. Будет здорово, если вы посвятите полчаса или даже час в день исключительно геометрии.
Только с помощью практики вы сможете достичь своей цели и освоить предмет на должном уровне. Сделайте решение 1-2 проблем в день своей привычкой. Со временем вы обнаружите, что решать задачи становится все легче, а находить правильные ответы — все интереснее.
Когда в классе обсуждается проблема и учитель предлагает вам попробовать решить ее на доске, отвечайте, даже если вы не знаете, как это сделать. Думайте. Учителя всегда рады, когда ученик действительно интересуется темой. Преподаватель обязательно ответит на ваши аргументы. Там, где это необходимо, он поможет. Направляйте ход мыслей в нужное русло. Они запомнят алгоритм и смогут самостоятельно применить его в следующий раз.
Использовать по желанию
Если геометрия вам совсем не дается, или вам нужно понять предмет не на школьном уровне, вы можете взять несколько уроков с репетитором. Индивидуальные занятия с репетитором почти всегда дают хорошие результаты. Репетитору даже не обязательно присутствовать лично. Благодаря современным технологиям можно организовывать уроки через Skype или другие подобные приложения.
Вот все советы, которые вам необходимы. Ничего сложного, а польза огромная. Просто следуйте им, и вы быстро добьетесь больших успехов в геометрии.
Как научиться решать задачи по аналитической геометрии? Типовая задача с треугольником на плоскости
Этот учебник предназначен для того, чтобы обеспечить приближение экватора между плоскостной геометрией и пространственной геометрией. На данном этапе нам необходимо систематизировать собранную информацию и ответить на очень важный вопрос: Как научиться решать задачи по аналитической геометрии? Сложность заключается в том, что существует бесконечное количество задач по геометрии, и ни один учебник не может вместить все многообразие и разнообразие примеров. Это не вопрос выведения функции с помощью пяти правил дифференцирования, таблицы и некоторых приемов…..
Решение есть! Я не буду утверждать, что придумал грандиозную технику, но, на мой взгляд, существует эффективный подход к проблеме, который даже полный дурак может использовать для достижения хороших или отличных результатов. По крайней мере, общий алгоритм решения геометрических задач сформировался в моем сознании очень четко.
Многие еще помнят со школьных времен точки равенства треугольников, точки подобия треугольников и утомительное заучивание доказательств теорем. Как сказал один из моих одноклассников: «Я не понимаю, зачем нужно … доказывать равенство треугольников, если вы видите, что они равны. Мы также ничего не докажем, потому что аналитическая геометрия смотрит на треугольник под совершенно другим углом.
Типичная задача о треугольнике на плоскости обычно формулируется следующим образом: Даны три вершины треугольника. Три треугольника из трех треугольников необходимы для… Многое требуется для того, чтобы найти…. Вам повезет, если там будет 3 или 4 пункта, но обычно их 5-6 и более.
Даны вершины треугольника. Требуется:
1) Напишите уравнения для сторон и найдите их углы? 2) Найдите длину стороны ? 3) найти ? 4) Составьте уравнение прямой, проходящей через точку, параллельную прямой ? 5) Напишите уравнение для контурной линии и найдите ее длину? 6) Вычислите площадь треугольника ? 7) Напишите уравнение для диаметра ? 8) Найдите точку пересечения.
Я чувствовал себя палачом с большим топором. Чтобы не смущаться, скажу, что на практике в большинстве случаев пунктов меньше. Я просто попытался объединить все, что может объединиться в одной проблеме. Дляособо опасныйэнтузиаст…виселицатри других элемента, но это только начало.
…бррр, у меня сегодня горе, хотя бы из-за последних нескольких часов дневного света. Думаю, сейчас я прихожу к решению.
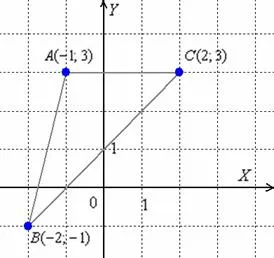
Решение: С чего начать? Хорошо начинать с плана. Не обязательно делать это в терминах, но для самоконтроля и самообладания всегда составляйте план в черновом варианте. Еще раз напоминаю, что наиболее удобная шкала — 1 единица = 1 см (2 тетрадные клетки).
Пойдемте расколем пару орехов:
1) Составьте уравнения для сторон и найдите их угловые коэффициенты.
Поскольку вершины треугольника известны, мы составим уравнения с двумя точками для каждой стороны. Эта процедура подробно рассматривается в уроке Уравнение прямой линии на плоскости.
Постройте уравнение стороны с :
Чтобы проверить это, нужно мысленно или графически подставить координаты каждой точки в полученное уравнение. Теперь определите угловой коэффициент. Для этого перепишите общее уравнение в уравнение с угловым коэффициентом:
Таким образом, угловой коэффициент равен :
Аналогично определите уравнения сторон. Я не вижу смысла писать одно и то же, поэтому через минуту приведу окончательный результат:
2) Найдите длину стороны. Это простейшая задача, рассматриваемая в уроке «Векторы для чайников». Для баллов мы используем формулу :
Используя ту же формулу, легко найти длины других сторон. С помощью обычной линейки это можно проверить очень быстро.
3) Найдите угол при вершине. Существует несколько способов решения этой задачи, но наиболее универсальным является нахождение угла при вершине как угла между векторами. Эта проблема подробно рассматривается в лекции «Скалярное произведение векторов».
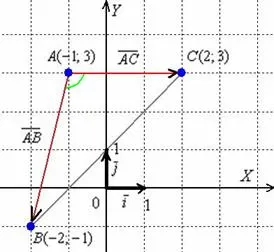
Кстати, у нас есть длины сторон .
Что ж, похоже на правду, для пущей убедительности можно подключить к углу угломер.
7 класс геометрия сложная тема, разъяснить подробно для детей
Решим более сложную задачу, в которой нужно доказать равенство треугольников и найти углы. Алгоритм решения проблемы:
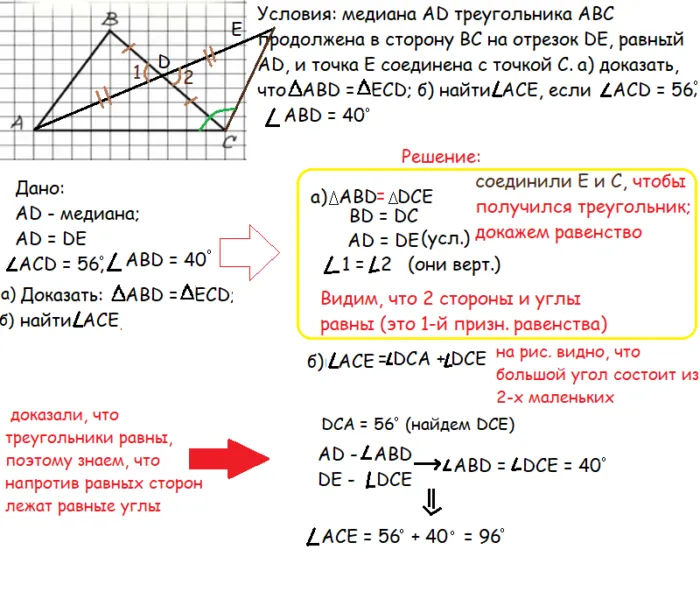
Шаг 1: Рисуйте в соответствии с условиями. Дан треугольник ABC, на котором проведена медиана (помните: медиана делит сторону на две половины). В нашей задаче медиана AD пересекает треугольник, создавая дополнительный отрезок DE (он равен AD). Получаем треугольник, из которого выводится медиана.
Шаг 2. Первая задача — доказать, что треугольники ABD и ECD равны: Соедините точки E и C, чтобы образовать треугольник.
Шаг 3. Предположим, что AD и DE равны (одна сторона треугольника равна другой стороне ⇒ AD = DE.
Шаг 4. Имеем BD = DC, так как медиана пересекает BC (получается, что еще одна сторона треугольника равна).
Шаг 5. Посмотрите на углы между сторонами (обозначены 1 и 2 на рисунке). Они вертикальны, потому что образованы двумя прямыми линиями. Следовательно, они равны.
Из первого доказательства равенства треугольников мы знаем, что если две стороны и угол между этими сторонами треугольника равны во втором треугольнике, то они также равны. Пункт а доказан. Продолжить с б.
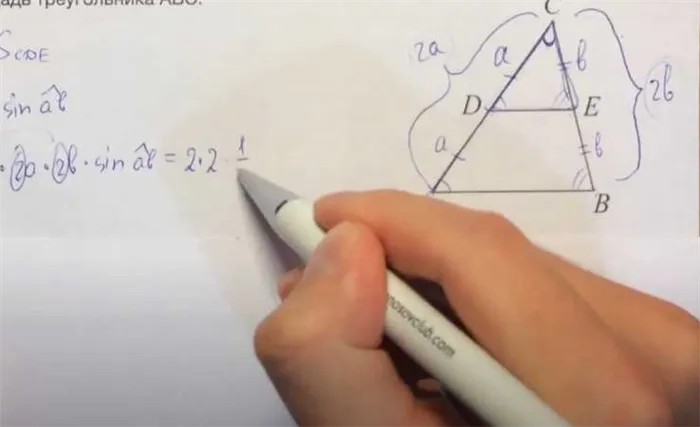
Шаг 1. Необходимо найти угол ACE. Из рисунка видно, что он состоит из 2 малых углов, поэтому получаем: угол ACE равен сумме углов DCA и DCE.
Шаг 2. Согласно условиям, мы знаем, чему равна DCA, теперь нужно найти второе значение. Доказав равенство треугольников, применим правило: Противоположные равные стороны треугольников имеют равные углы. AD напротив ABD; DE напротив DCE. Из этого следует, что: Угол ABD = Угол DCE = 40 градусов (по условию).
Шаг 3. Малые углы известны, найдите требуемый: Угол ACE = 56º + 40º = 96º.
Равенство доказано, угол найден. Проблема решена.
Больше видео по решению задачи на правильный треугольник и всей задачи по геометрии 7 класса в одном задании.








