Конструкция этого типа двигателя отличается от конструкции двигателей постоянного тока, в которых проводящая рамка вращается в поле постоянных магнитов. Большое количество рамок удерживают якорь, а ряд электромагнитов образуют основу статора. В трехфазных машинах переменного тока все происходит наоборот.
Основные пункты
- Длина дуги Δs – дистанция, пройденная по круговой траектории. R – радиус кривизны кругового пути.
- Угол поворота – величина вращения, соответствующая линейной дистанции. Вычислим угол поворота Δθ как соотношение длины дуги к радиусу кривизны: Δθ = Δs/r.
- Для одного полного оборота угол поворота равняется 2π.
- Угловое положение – угол в радианах (градусы, обороты), через которые точку или линию повернули в определенном направлении вокруг указанной оси.
Когда объекты вращаются вокруг оси (вращение CD), каждая точка движется по дуге. Проведите линию от центра диска к краю. Каждая ось, используемая для записи звука вдоль линии, перемещается на угол и временной интервал.
Угол поворота — это величина поворота, соответствующая линейному расстоянию. Вычислим угол поворота Δθ как отношение длины дуги к радиусу кривизны:
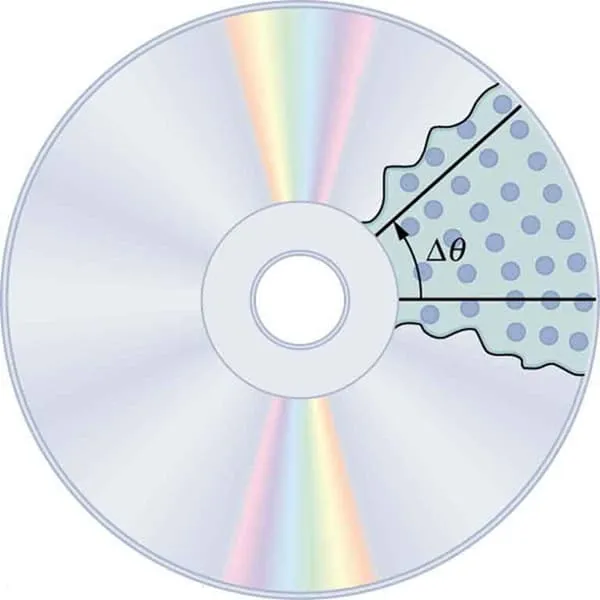
Все точки на компакт-диске движутся по круговым дугам. Впадины вдоль линий от центра к краю перемещаются на угол Δ за период Δt.
В математике угловое положение — это мера количества, на которое объект вращается вокруг фиксированной точки.
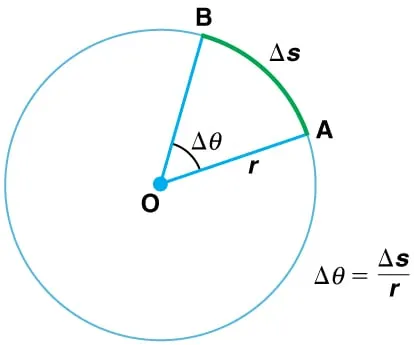
Радиус окружности поворачивается на угол Δ. Длина дуги Δs описывается следующей зависимостью.
Длина дуги Δs — это расстояние, пройденное по круговому пути. R — радиус кривизны круговой траектории. Для полной окружности длина дуги соответствует объему круга радиусом r. Объем круга = 2πr. Видно, что для полного вращения угол поворота:
Это является основой для расчета единиц, используемых для измерения углового положения лучей:
2π рад = 1 оборот.
Когда Δθ = 2π рад, компакт-диск совершил полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку окружность занимает 360°, связь между радиусом и градусом равна 2π рад = 360°, следовательно:
1рад = 360°/2π = 57,3°.
Угловое перемещение (угол поворота)
Угловое перемещение (угол поворота) — это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Δφ-угол движения при движении тела по окружности.
Единицей измерения угла поворота является 1 радиус 1 рад. Радиус — это угол, опирающийся на дугу окружности, равную ее радиусу.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Предполагая, что в начальный момент времени φ0= 0, угловое смещение (угол поворота) часто обозначается φ.
Если известны угловая скорость и время вращения, можно определить угол поворота:
Δφ, φ — угловое смещение (угол поворота).
R — радиус окружности
ω — угловая скорость
t — время, за которое было выполнено вращение.
Вопросы к экзамену
Для студентов всех технических профильных групп Новороссийского колледжа строительства и экономики (НКТЭЭ).
- Главная
- Мир физики
- Физика в формулах
- Теоретические сведения
- Физический юмор
- Физика вокруг нас
- Физика студентам
Для улучшения работы сайта и его взаимодействия с пользователями мы используем файлы cookie, которые хранятся на вашем компьютере. Нажимая кнопку «СОГЛАСЕН», вы подтверждаете, что были проинформированы об использовании файлов cookie на нашем сайте и согласны с их использованием. Вы можете отключить файлы cookie в настройках своего браузера.
- Тестирование
- Обратная связь
- Обо мне
- Карта сайта
- Правообладателям
- Политика конфиденциальности
В настоящее время на сайте 189 посетителей и нет зарегистрированных пользователей
Если вы являетесь автором материала или правообладателем и возражаете против его использования на моем сайте, пожалуйста, свяжитесь со мной. Информация будет удалена в кратчайшие сроки.
Спасибо авторам и правообладателям, которые соглашаются на публикацию своих материалов на моем сайте! Вы вносите неоценимый вклад в образование, воспитание и развитие будущего поколения.
© 2022 Дудко Елена | Infofiz.ru 2011-2022 | Все права защищены | Все материалы взяты из открытых источников и представлены на локальном компьютере только в ознакомительных целях. Все права на статьи, книги, видео- и аудиоматериалы принадлежат соответствующим авторам и издателям. Распространение и/или коммерческое использование не допускается без разрешения правообладателей. .
Содержание материала
Существует большое количество вычислительных задач, которые моделируют явления, происходящие в различных вращающихся объектах или вблизи них. В такой численной задаче важно выбрать физически корректный и вычислительно оптимальный способ описания вращения в численной модели. FlowVision позволяет задавать вращение различными способами: с вращающейся локальной системой координат, с движущимися телами и с поверхностями скольжения. Чтобы помочь пользователю понять эти типы задач, были рассмотрены примеры различных типов задач, начиная с основ физики и математики.
1.1. Вращательное движение материальной точки
Вращательное движение материальной точки (m.t.) вокруг неподвижной оси — это движение материальной точки по окружности радиуса R, центр которой лежит на прямой (оси вращения), неподвижной относительно данной системы отсчета и перпендикулярной плоскости, в которой лежит путь точки.
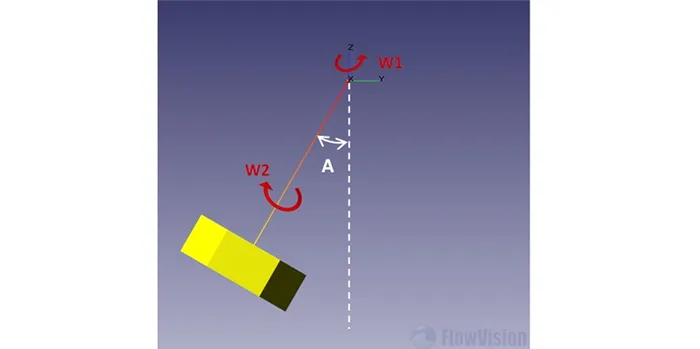
Рисунок 1.
Вращательное движение тела вокруг неподвижной оси — это движение тела, когда все его точки, движущиеся в параллельных плоскостях, описывают окружности, центры которых лежат на одной и той же неподвижной прямой, называемой осью вращения. Тело во вращательном движении имеет одну степень свободы, и его положение относительно данной системы отсчета определяется углом поворота φ между неподвижной полуплоскостью и полуплоскостью, жестко связанной с телом и проходящей через ось вращения.
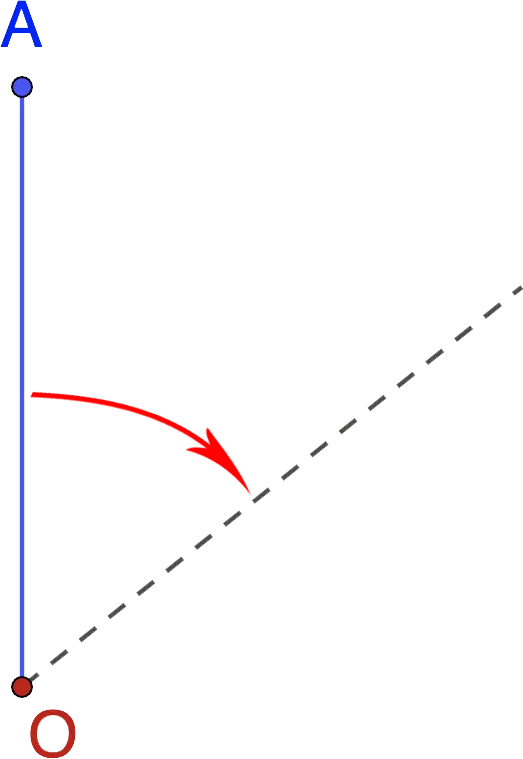
Рисунок 2.
1.2. Угол поворота
Угол φ считается положительным при движении по часовой стрелке от неподвижной плоскости (для наблюдателя, смотрящего с положительного конца оси az) и отрицательным при движении по часовой стрелке. Чтобы узнать положение в любой момент времени, нам нужно знать зависимость угла φ от времени t, т.е. φ=f(t).
1.3. Основные кинематические характеристики вращательного движения
Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение. Угловая скорость и угловое ускорение величины векторные. Вектор угловой скорости направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки (рис.3). Такой вектор определяет сразу и модуль угловой скорости, и ось вращения, и направление вращения вокруг этой оси. Аналогично углу поворота, когда вращение происходит против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az) ω>0, а когда по ходу часовой стрелки, то ω
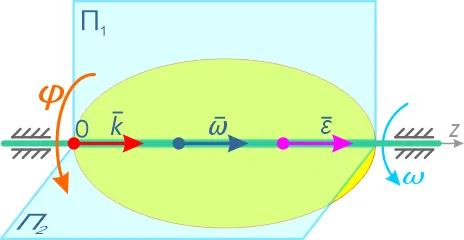 а)
а)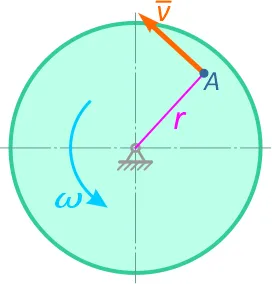 б)
б)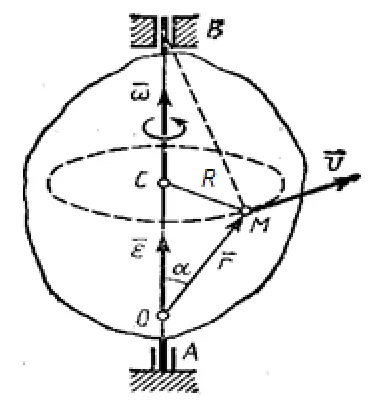 в)
в)1.4. Прочие кинематические характеристики
Скорость точки M на расстоянии R от оси (рис. 2):
Тангенциальная составляющая ускорения точки M (рис. 3b):
Нормальная составляющая ускорения точки M (рис. 3b):
Полное ускорение точки М (рис. 3б):
Формула Эйлера (рисунок 3c):
Силы инерции, действующие на материальную точку во вращающейся системе отсчета
2.1. Материальная точка, покоящаяся во вращающейся системе отсчета
Учитывая движение вращающейся точки M, сила, действующая на нее относительно неподвижной системы координат (SK) XYZ (рис. 4a), может быть определена по второму закону Ньютона: Относительно вращающейся системы координат X’Y’Z’ точка M неподвижна (рис. 4b), поскольку результирующая сила уравновешивается инерционной силой (центробежной силой): .
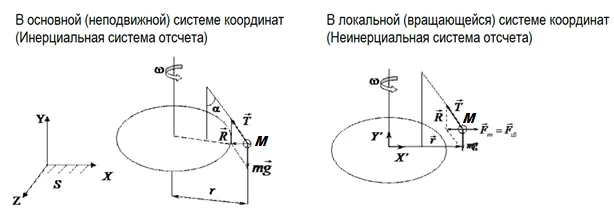
Рис. 4(a,b)
2.2. Материальная точка, движущаяся во вращающейся системе отсчета
Если точка движется во вращающейся системе отсчета, на нее действует сила Кориолиса в дополнение к центробежной силе (рис. 5). Направление силы Кориолиса определяется правилом правого винта.
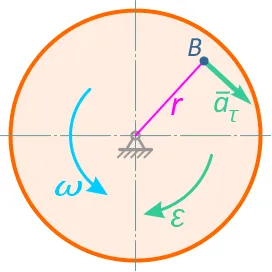
Рисунок 5.
Таким образом, при переходе от фиксированной CP к локальной CP, которая является вращающейся системой отсчета, появляются дополнительные компоненты вектора силы, действующей на материальную точку: центробежная сила и сила Кориолиса.








