Доказательство правильности этой конструкции достаточно интуитивно и основано на симметрии задачи. Трисекция угла (разделение его на три равные части) не может быть выполнена только с помощью компаса и линейки (это впервые доказал Пьер Ванзель).
Геометрия: свойства треугольника
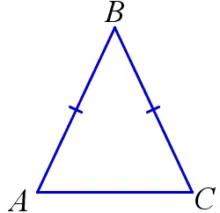
Треугольник — это геометрическая фигура, состоящая из трех точек, не лежащих на прямой линии (вершины треугольника), и трех отрезков, концы которых лежат в этих точках (стороны треугольника).
На иллюстрации: Треугольник ABC; A, B, C — вершины треугольника ABC; AB, AC, BC — стороны треугольника ABC; ∠BAC, ∠ABC, ∠ACB — углы треугольника ABC.

- Треугольник называется остроугольным, если все его углы острые.
- Треугольник называется тупоугольным, если один из его углов тупой.
- Треугольник называется прямоугольным, если один из его углов прямой. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
- Равнобедренный треугольник — треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны.
Свойства сторон треугольника
- Сумма любых двух сторон треугольника больше его третьей стороны. На рисунке: b+c>a, a+c>b, a+b>c.
- Длина каждой стороны треугольника больше разности длин двух других сторон. На рисунке: |a-b|

Высота треугольника — это перпендикуляр, проведенный из любой вершины треугольника к противоположной стороне или к продолжению стороны. На иллюстрации.
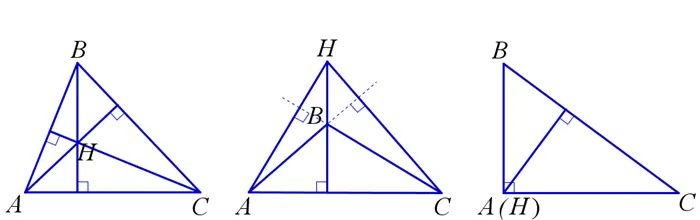
Высоты треугольника пересекаются в точке, называемой ортоцентром треугольника. На рис: H — центр правой стороны треугольника ABC.
Прямая теорема о серединном перпендикуляре
Рисунок 2. Иллюстрация теоремы.
Каждая точка, лежащая на перпендикуляре из центра, равноудалена от краев отрезка.
Докажите, что
Они являются правильными треугольниками и равны, так как имеют общий зонд OM, а зонды AO и OB равны по условию, поэтому мы имеем два правильных треугольника, равных по двум зондам. Отсюда следует, что гипотенузы треугольников также равны, т.е,
Обратная теорема верна.
Обратная теорема о серединном перпендикуляре
Любая точка, равноудаленная от концов отрезка, находится в средней точке перпендикуляра этого отрезка.
Дан отрезок AB, середина p перпендикуляра к нему, точка M, равноудаленная от концов отрезка. Докажите, что точка M находится в средней точке перпендикуляра на отрезке (рисунок 3).
Рисунок 3. Иллюстрация теоремы.
Рассмотрим треугольник по условию. Рассмотрим медиану треугольника: Точка O является центром основания AB, а OM — медианой. Согласно свойству равнобедренного треугольника, медиана, проведенная к основанию, является одновременно высотой и биссектрисой. Из этого следует, что
Прямая и обратная теоремы могут быть обобщены.
Теорема о пересечении серединных перпендикуляров треугольника
Точка лежит на серединном перпендикуляре отрезка только в том случае, если она равноудалена от концов отрезка.
Повторим, что в треугольнике три отрезка и для каждого из них выполняется свойство перпендикуляра к центру.
Теорема:
Медианы треугольника пересекаются в точке.
Дан треугольник 1 1.на стороне BC, P2на стороне переменного тока, P3на стороне АВ.
Докажите, что перпендикуляры P1, Р2и P3пересекаются в точке O (рисунок 4).

Рисунок 4. Иллюстрация теоремы.
Рассмотрим две промежуточные точки P2и P3и пересекаются, существует точка пересечения О. Докажите этот факт обратным методом — пусть перпендикуляры P2и P3параллельны. Тогда угол равен. Следовательно, существует точка пересечения O двух из трех средних точек. Свойства точки O: Она находится на середине перпендикуляра к стороне AB, поэтому равноудалена от краев AB: Получим следующие уравнения:
Из этого равенства нас интересует тот факт, который необходимо было доказать.
Основные элементы треугольника abc

Углы a, b, c образованы тремя парами сторон. Углы часто обозначаются так же, как и вершины — буквами A, B и C.
Угол, образованный сторонами треугольника и лежащий внутри треугольника, называется внутренним углом, а угол, касательный к нему, — соседним углом треугольника (2, с. 534).
Высоты, медианы, биссектрисы и средние линии треугольника
Помимо основных элементов треугольника, рассматриваются и другие сегменты с интересными свойствами: Высоты, медианы, биссектрисы углов и медианы.
Высоты треугольника — это перпендикуляры, проведенные из вершин треугольника к противоположным сторонам.
Чтобы нарисовать высоту, выполните следующие действия:
1) Проведите линию, содержащую одну из сторон треугольника (если высота проведена из вершины острого угла в тупоугольном треугольнике),
2) Из вершины, противоположной нарисованной прямой, проведите отрезок от этой точки до прямой, образующей с ней угол 90 градусов.
Пересечение высотомера с одной из сторон треугольника называется основанием высотомера (см. рисунок 2).
Свойства высот треугольника
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному треугольнику.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон.
- Три высоты в остроугольном треугольнике пересекаются в одной точке и эту точку называют ортоцентром треугольника.
Медианы (от лат. mediana – «средняя») – это отрезки, соединяющие вершины треугольника с серединами противолежащих сторон (см. рис. 3). Для построения медианы необходимо выполнить следующие действия: 1) найти середину стороны; 2)соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком. Свойства медиан треугольника
- Медиана разбивает треугольник на два треугольника одинаковой площади.
- Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделен диагоналями на шесть равных треугольников.
Точка пересечения биссектрис треугольника – тупоугольного, правильного, остроугольного, равнобедренного
В треугольнике есть три характерные линии: контурные линии, медианы и биссектрисы. Для каждой из этих линий существует точка пересечения, которая характеризует треугольник. Первой точкой всегда является точка пересечения биссектрис углов, поскольку она предоставляет информацию о связи между величинами треугольника и связанных с ним окружностей.

Определение
Точка пересечения биссектрис углов — одна из самых проблемных точек. Это приводит к пониманию вписанных и обведенных фигур, которое очень трудно усвоить. Мы должны думать не только о треугольнике, но и об окружностях, внутренней окружности и перикруге, что делает решение задачи очень трудным.
С другой стороны, значения радиусов конца и перикруга фигурируют во многих формулах, что облегчает нам решение многих задач. Но сначала нам нужно понять, что такое акроцикл и перицикл, а затем узнать, связаны ли они с пересечением биссектрис углов и как.
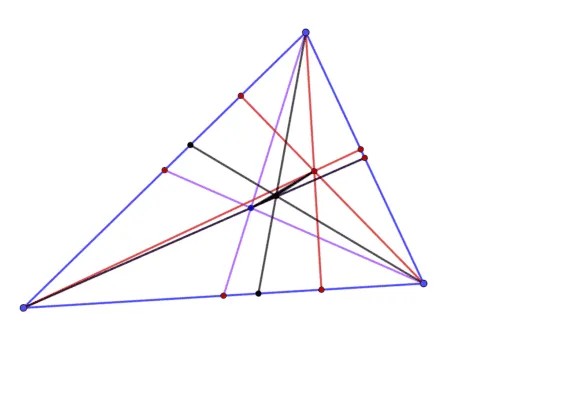
Рисунок 1. Золотое сечение треугольника.
В любом остроугольном треугольнике характерные точки не совпадают, и если их соединить, то получится золотое сечение треугольника, тогда как в обычном треугольнике золотое сечение — это точка. В равнобедренном треугольнике золотое сечение становится линией.
Окружность — это окружность, которая касается каждой из сторон треугольника.
Центр такой окружности называется центром треугольника. Центр или точка пересечения биссектрис тупоугольного треугольника всегда находится внутри треугольника, в отличие от высот.
Расстояние от эпицентра одинаково с обеих сторон и соответствует радиусу вершинной окружности. В этом случае треугольник считается периметрическим.
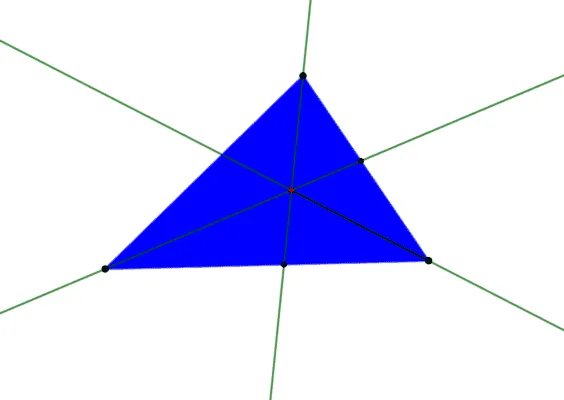
Рисунок 2. Центр треугольника
Перицикл — это окружность, касательная к каждой вершине треугольника. То есть, каждая вершина должна входить в границу круга. И наоборот, в этом случае треугольник является вписанным, а расстояние между вершинами треугольника и центром окружности всегда равно радиусу окружности.
Теоремы о точке пересечения биссектрис
Теорема на самом деле одна, но доказательство разделено на две части. Формулировка выглядит следующим образом: Биссектрисы треугольника пересекаются в одной точке, и эта точка является центром окружности.
Сначала докажите, что три биссектрисы углов пересекаются в одной точке. Это делается путем проведения биссектрис Bm, CP и AK в треугольнике ABC. Обозначим точку пересечения буквой O. Затем рассмотрим каждую биссектрису угла отдельно. Для биссектрисы угла AK расстояния от сторон треугольника a и c должны быть равны; для биссектрисы угла CP расстояния c и a должны быть равны. Для биссектрисы BM расстояния c и c должны быть равны. Отрезки a, c и c равны между собой по свойству биссектрисы угла: каждая геометрическая точка биссектрисы угла равноудалена от сторон угла.
И может быть только одна точка, равноудаленная от каждой стороны. Просто попробуйте поместить точку пересечения в другую точку, и вы сразу же обнаружите, что условие не выполняется, что невозможно.
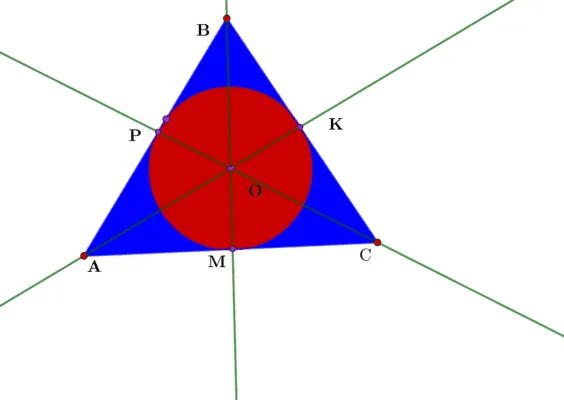
Рисунок 3. чертеж для решения задачи
Мы уже говорили, что в треугольнике только одна точка может быть равноудалена от всех сторон. Это означает, что окружность с центром в этой точке вписана в треугольник, так как радиус этой окружности перпендикулярен стороне треугольника. Теперь докажите, что в треугольнике может быть только одна вписанная окружность. Если перенести точку в другую точку треугольника и опустить перпендикуляры на стороны, то станет ясно, что перпендикуляры не равны, а значит, центр не может находиться в этой точке. Это то, что вы должны были доказать.
Биссектрисы площади и биссектрисы периметра
Треугольник
Есть бесконечное множество линий, которые делят пополам площадь треугольника. Три из них являются медианами треугольника (которые соединяют середины сторон с противоположными вершинами), и они параллельны в центроиде треугольника; действительно, они единственные биссектрисы площади, проходящие через центроид. Три другие биссектрисы площади параллельны сторонам треугольника; каждая из них пересекает две другие стороны, чтобы разделить их на сегменты с пропорциями 2 + 1: 1>+ 1: 1>. Эти шесть линий одновременно являются тремя: помимо того, что три медианы совпадают, каждая медиана параллельна двум биссектрисам площади, которые параллельны сторонам.
Огибающая бесконечных биссектрис квадрата представляет собой дельтоид (обычно определяемый как фигура с тремя вершинами, соединенными вогнутыми кривыми на внешней стороне дельтоида, что делает внутренние точки невыпуклым множеством). Вершины дельтоида лежат в середине промежутков; все точки внутри дельтоида лежат на трех биссектрисах разных областей, а все точки вне дельтоида — только на одной. 1 Стороны дельтоида — гиперболические дуги, асимптотические к длинным сторонам треугольника. Отношение площади биссектрисы дельты к площади треугольника одинаково для всех треугольников и равно 3 4 log e (2) — 1 2,<4>>\ log _ (2) ->,>т.е. 0,019860. или менее 2%.
Биссектриса треугольника — это отрезок прямой, который пересекает периметр треугольника и имеет конечную точку в середине одной из трех сторон. Три щели совпадают с центром круга Шпикера, который является окружностью центрального треугольника. Луки идут параллельно биссектрисам угла.
Граница треугольника — это прямая линия, заканчивающаяся в одной из трех вершин треугольника и образующая половину его окружности. Три делителя совпадают в точке ногтя треугольника.
Любая прямая, проходящая через треугольник и рассекающая площадь треугольника и его периметр, проходит через центр треугольника (центр внутренней окружности). Для данного треугольника их может быть один, два или три. Линия, проходящая через центр внутреннего пространства, пересекает одну из областей или периметров только в том случае, если она пересекает другую.
Параллелограмм
Любая прямая, проходящая через центр параллелограмма, делит его площадь и периметр на две части.
Окружность и эллипс
Все биссектрисы площади и биссектрисы окружности круга или другого эллипса проходят через центр, а каждая хорда, проходящая через центр, биссектриса площади и окружности. В случае с кругом это диаметры круга.
Биссектрисы объема
Плоскость, которая делит два противоположных ребра четырехугольника в определенном соотношении, также делит объем четырехугольника в том же соотношении. Таким образом, любая плоскость, содержащая биссектрису (соединение центров противоположных граней) тетраэдра, делит объем тетраэдра пополам.
- ^Вайсштейн, Эрик У. «Биссектриса внешнего угла». Материал из MathWorld — веб-ресурс Wolfram.
- ^Испания, Барри. Аналитические коники, Dover Publications, 2007 (источник 1957).
- ^ Джонсон, Роджер А., Advanced Euclidean Geometry, Dover Publ., 2007 (исходный текст 1929 г.).
- ^Оксман, Виктор. «О существовании треугольников с заданной длиной одной стороны и двумя смежными биссектрисами», Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
- ^Саймонс, Стюарт. Mathematical Gazette 93, март 2009 г., стр. 115-116.
- ^Миронеску П. и Панаитопол Л., «Существование треугольника с предписанной длиной биссектрисы», American Mathematical Monthly 101 (1994): 58–60.
- ^Оксман Виктор, «Чисто геометрическое доказательство единственности треугольника с предписанными биссектрисами», Forum Geometricorum 8 (2008): 197–200.
- ^Вайсштейн, Эрик У. «Четырехугольник». Материал из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Quadrateral.html
- ^ Митчелл, Дуглас В. (2013), «Биссектрисы сторон треугольника», Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
- ^Альтшиллер-Корт, Натан, College Geometry, Dover Publ., 2007.
- ^ Данн, Дж. А., и Претти, Дж. Э, «Халвинг» треугольник «Mathematical Gazette 56, May 1972, 105-108.
- ^Кодокостас, Димитриос, «Triangle Equalizers», Mathematics Magazine 83, апрель 2010 г., стр. 141–146.
- ^Данн, Дж. А. и Дж. Э. Претти, «Деление треугольника пополам», Mathematical Gazette 56, май 1972 г., стр. 105.
- ^Вайстейн, Эрик В. «Тетраэдр». Материал из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/Tetrahedron.html
- ^Альтшиллер-Корт, Н. «Тетраэдр». Гл. 4 в Modern Pure Solid Geometry: Chelsea, 1979.
Внешние ссылки
- Биссектриса угла в точке срезать узел
- Определение биссектрисы угла. Math Открыть справочник С интерактивным апплетом
- Определение биссектрисы линии. Math Open Reference С интерактивным апплетом
- Биссектриса перпендикулярной линии. С интерактивным апплетом
- Анимированные инструкции для деления угла пополам и деления линии пополам Использование циркуля и линейки
- Вайсштейн, Эрик У.«Биссектриса линии». MathWorld.
В этой статье использованы материалы со страницы Угловая биссектриса на PlanetMath, распространяемые по лицензии Creative Commons Attribution/Share-Alike License.








