Гистограммы представлены в виде вертикально вытянутых прямоугольников (полос), высота которых соответствует значению индекса (рисунок 6.9).
Гистограммы используются для описания дисперсии, динамики и взаимосвязей. Линейные графики строятся на сетке координат. Геометрические точки — это точки и отрезки прямых, последовательно соединенные пунктирными линиями.
Линейные диаграммы используются для характеристики динамики в следующих случаях:
- если количество уровней ряда динамики достаточно велико. Их применение подчеркивает непрерывность процесса развития в виде непрерывной линии;
- с целью отображения общей тенденции и характера развития явления;
- при необходимости сравнения нескольких динамических рядов;
- если нужно сопоставить не абсолютные уровни явления, а темпы роста.
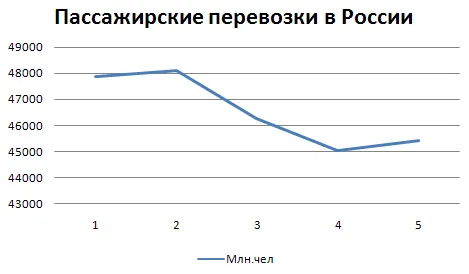
При представлении динамики с помощью линейного графика временные характеристики (дни, месяцы, кварталы, годы) отображаются на оси пропасти, а значения показателя (пассажиропоток в России) — на оси линии.
Таблица. Перевозка пассажиров транспортом общего пользования в России
| Годы | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| млн. чел. | 47885 | 48114 | 46283 | 45037 | 45412 | 45817 |
Несколько кривых могут быть нанесены на один линейный график (рис. 1) для сравнения динамики различных показателей или одного и того же показателя в различных регионах, секторах и т.д.
Для построения этого графика мы воспользуемся данными о динамике производства овощей и картофеля в России.
Производство овощей в России, млн тонн
| Годы | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Картофель | 38,3 | 37,7 | 33,8 | 39,9 | 38,7 | 37,0 |
| Овощи | 10,0 | 9,8 | 9,6 | 11,3 | 10,7 | 11,1 |
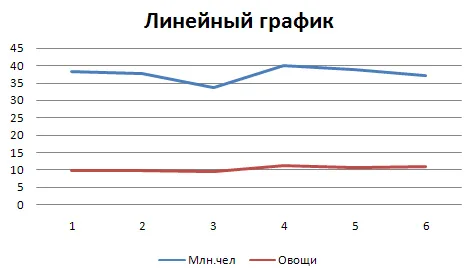
Рисунок 1. Динамика производства картофеля и овощей в России в 2006-2011 гг.
Логарифмическая диаграмма
Однако линейные графики с равномерной шкалой искажают относительные изменения экономических показателей. Более того, их использование теряет четкость и даже становится невозможным при представлении динамических рядов с сильно меняющимися уровнями, что характерно для динамических рядов за длительный период времени. В этих случаях вместо равномерной шкалы используется полулогарифмическая сетка, где на одной оси нанесена линейная шкала, а на другой — логарифмическая. В этом случае на оси порядка откладывается логарифмическая шкала, а ось бездны используется для отсчета времени через приемлемые интервалы (год, квартал и т.д.). Постройте логарифмическую шкалу: Определите логарифмы исходных чисел, начертите упорядоченную шкалу и разделите ее на несколько равных частей. Затем начертите на упорядоченной шкале части, соответствующие абсолютным приращениям этих логарифмов, и запишите соответствующие логарифмы чисел и их аналогов.
Полученные антилогарифмы дают вид желаемого масштаба на упорядоченной шкале.
| Логарифмы чисел | Цифры |
| 3,0 | 1000 |
| 2,8 | 317 |
| 2,0 | 100 |
| 1,5 | 31,7 |
| 1,0 | 10 |
Рассмотрим пример использования логарифмической шкалы для иллюстрации динамики производства кассовых аппаратов в России:
| Годы | Производство, тыс. шт. | Логарифмы уровней |
| 2006 | 32,5 | 1,5119 |
| 2007 | 81,2 | 1,9096 |
| 2008 | 202,0 | 2,3054 |
| 2009 | 368,0 | 2,5658 |
| 2010 | 203,0 | 2,3075 |
| 2011 | 220,0 | 2,3424 |
Найдя минимальное и максимальное значения логарифмов выходных данных кассового аппарата, постройте шкалу для нанесения всех значений на график. Затем найдите соответствующие точки (с учетом масштаба) и соедините их прямыми линиями. Полученная диаграмма (см. рис. 2) с логарифмической шкалой называется диаграммой полулогарифмической сетки.
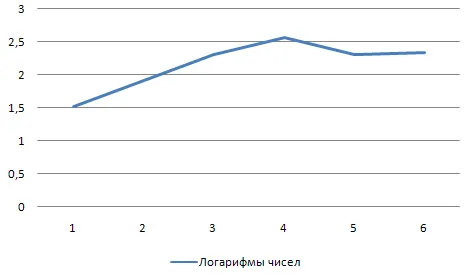
Рис. 2. динамика производства кассовых аппаратов в России в 2006-2011 гг.
Радиальная диаграмма
Радиальные графики являются разновидностью линейных графиков. Они нарисованы в полярной системе координат, чтобы отразить процессы, ритмично повторяющиеся во времени. Радиальные диаграммы можно разделить на два типа: замкнутые и спиральные.
Замкнутые радиальные диаграммы строятся на основе центра окружности (Рисунок 3). Рисуется круг с радиусом, соответствующим среднемесячному значению рассматриваемого явления, который затем делится на двенадцать равных секторов. Каждый радиус представляет месяц, а расположение напоминает стрелки часов. Каждый луч маркируется в соответствии со шкалой, выбранной на основе данных за каждый месяц. Если данные превышают среднегодовое значение, отметка делается на продолжении луча за пределами круга. Затем отметки всех месяцев соединяются отрезками.
Рассмотрим пример замкнутой радиальной диаграммы на основе ежемесячных данных о грузовых перевозках по железной дороге общего пользования в России в 1997 году.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 1 | 1 |
| 68,9 | 67,6 | 776,3 | 70,7 | 71,3 | 74,2 | 76,3 | 75,7 | 79,3 | 74,9 | 74,0 | 74,2 |
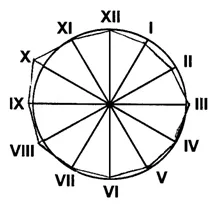
Рисунок 3. Грузовые перевозки на железнодорожном транспорте общего пользования.
Радиальные спиральные графики используют круг в качестве точки отсчета. Декабрь одного года связан с январем следующего года, так что весь ряд трендов может быть представлен в виде одной кривой. Такой график особенно нагляден, когда, помимо сезонной закономерности, наблюдается также устойчивый рост уровня ряда.
Столбчатая диаграмма (Bar Graph)
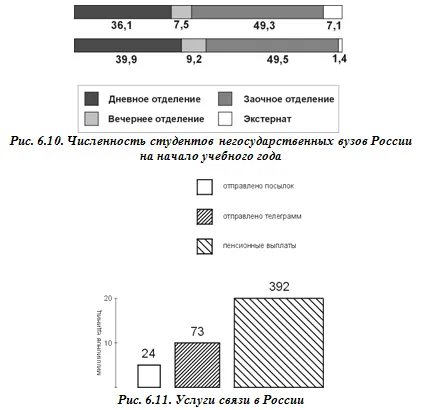
Вероятно, это был первый метод визуализации, с которым вы столкнулись. Вспомните свои школьные учебники, там было много таких таблиц. Если вы думали, что столбчатые диаграммы отошли на второй план в школе, не спешите с ними прощаться. С их помощью можно легко представить многие типы данных: Информация о трафике, рост числа клиентов, графики продаж. Гистограммы — один из самых очевидных способов представления статистических данных.
Линейная диаграмма (Line Chart)

Этот тип графика напоминает вершины горного хребта, и сравнение не случайно. Гистограммы позволяют отобразить горы данных и получить максимум информации. Они подходят для демонстрации колебаний акций, темпов роста компании, построения прибыльной системы.
Гистограмма с несколькими осями (Multi-Axis Charts)
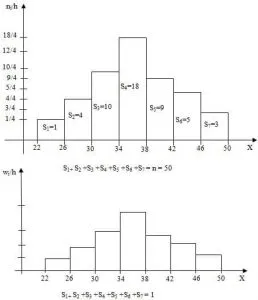
Это комбинация гистограммы и линейной диаграммы. Он подходит, когда необходимо показать два или более факторов для выявления параллелей или сравнений. Гистограммы с осями часто используются на заседаниях совета директоров компаний, например, для сравнения рыночной цены и общего дохода.
Секторная диаграмма
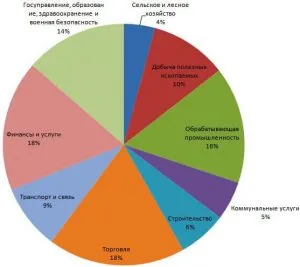
Круговые диаграммы используются для иллюстрации структуры (состава) населения. Круговая диаграмма строится путем деления круга на сегменты, соответствующие весу сегментов в целом. Размер каждого сектора определяется величиной расчетного угла (1% равен 3,6 0 ).
Пример. На долю продуктов питания приходилось 55% российских розничных продаж в 1992 году и 49% в 1997 году; на долю непродовольственных товаров — 45% и 51% соответственно.
Начертите две окружности одинакового радиуса и установите центральные углы для обозначения секторов: для пищевых продуктов 3,6 0 0 *55 = 198 0, 3,6 *49 = 176,4 0, для непищевых продуктов 3,6 0 0 *45 = 162 0, 3,6 0 *51 = 183,6 0. Разделите круги на соответствующие сектора (рис. 6.12).
Треугольная диаграмма
Треугольная диаграмма — это тип диаграммы, который представляет собой структуру (в дополнение к столбиковой и полосовой диаграмме). Он используется для одновременного отображения трех значений, которые представляют собой элементы или компоненты величины. Треугольная диаграмма — это равносторонний треугольник, каждая сторона которого представляет собой равномерную шкалу от 0 до 100. Внутри него находится сетка координат, соответствующих линиям, проведенным параллельно сторонам треугольника. Перпендикуляры из каждой точки координатной сетки представляют доли трех компонентов, которые в сумме соответствуют 100% (Рисунок 6.13). Одна точка на диаграмме соответствует 20% (для A), 30% (для B) и 50% (для C).
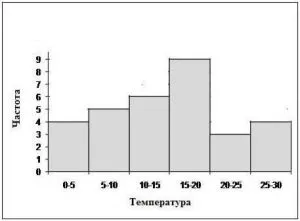
Рисунок 6.13. Треугольная диаграмма
Наглядное представление статистической информации
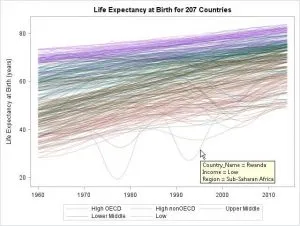
На этом уроке мы сформулируем идеи для визуального представления статистических данных. Мы введем определение графа. Мы также вспомним, как строить столбчатые диаграммы, круговые диаграммы, полигоны и гистограммы.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим учебным видео в комплекте, вам необходимо добавить их в свой личный кабинет.
2. Распределите видеоуроки по личным кабинетам ваших учеников.

3. Смотрите статистику просмотра видеоуроков учениками.
Конспект урока «Наглядное представление статистической информации»
Еще в 7 классе на уроке алгебры мы изучали одну из самых интересных подобластей математики — статистику.
Давайте вспомним определение статистики. Итак, статистика — это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях в обществе и природе.
В современном обществе статистика стала одним из важнейших инструментов управления. Он собирает информацию, описывающую развитие экономики, культуры и уровень жизни жителей страны. С помощью статистической методологии вся полученная информация обобщается, анализируется и тем самым дает возможность увидеть систему взаимосвязей, наглядную картину и динамику развития.
Умение работать со статистическим материалом в различных формах необходимо каждому, поскольку он постоянно встречается во всех источниках информации, адресованных массовой аудитории — в газетах, журналах, книгах, на телевидении и т.д.

Определение:
Диаграмма (от греческого diagramma, что означает «рисунок, эскиз») — это графическое изображение, иллюстрирующее взаимосвязь между различными величинами. Это один из способов представления информации.
Диаграмма — это разновидность математической модели.
Вы уже знакомы с диаграммами. Итак, с какими диаграммами вы знакомы?
Гистограммы. Они используются, когда вы хотите проиллюстрировать динамику данных во времени или распределение данных в статистическом исследовании.
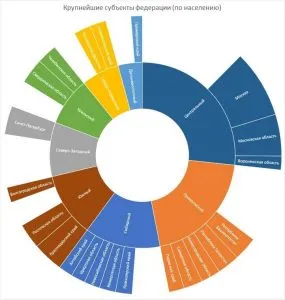
Пример: В конце учебного года у нас был итоговый тест по математике. Результаты теста были следующими: «Два» получили 3 студента, «три» — 6 студентов, «четыре» — 11 студентов и «пять» — 7 студентов. Вся эта информация может быть сведена в таблицу. Эти данные также могут быть представлены в виде гистограммы. На вертикальной оси отметьте количество студентов, получивших ту или иную оценку, а на горизонтальной оси — оценки. Гистограмма, построенная на основе приведенных выше данных, имеет следующую форму:
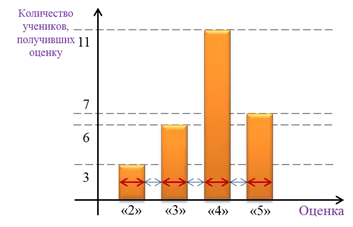
Он состоит из четырех прямоугольников. Помните, что все прямоугольники в гистограмме должны иметь одинаковую ширину и располагаться на одинаковом расстоянии друг от друга.
В статистическом исследовании, когда аналогичные данные сгруппированы и для каждой группы указана соответствующая частота (или относительная частота), каждая группа представлена на гистограмме прямоугольником, высота которого на выбранной шкале соответствует соответствующей частоте (или относительной частоте).
Удобно использовать круговые диаграммы для наглядного представления взаимосвязей между исследуемыми сегментами населения.

Несколько групп — тесты
Рассмотрим проверку гипотезы, сравнивающую различные группы. Для простоты мы сосредоточимся на наиболее популярном F-тесте.
F-тест
Этот тест сравнивает дисперсию переменной между группами и также называется дисперсионным анализом (ANOVA).
Статистика F-теста определяется следующим образом:
Где G — число групп, N — число наблюдений, x̅ — общее среднее, x̅g — среднее в группе g. При нулевой гипотезе о независимости групп f-статистика имеет F-распределение.
from scipy.stats import f_oneway Группы доходов = df.locdf'Arm'==arm, 'Income'.values for arm in df'Arm'.dropna().unique() stat, p_value = f_oneway(*группы доходов) print(f "F Test: statistic=, p-value=") F Test: statistic=9.0911, p-value=0.0000p-значение теста близко к нулю, что означает четкое отклонение нулевой гипотезы об отсутствии разницы в распределении доходов между типами лечения.
Код
И пока мы сравниваем распределения, мы помогаем вам улучшить свои навыки или освоить смежную профессию, причем с самого начала:
Ссылки
8 Р. фон Мизес,вероятностная статистика и истина(1936), Бюллетень Американского математического общества.








