Рассмотренный пример является «открытой проблемой» — можно рассмотреть решение целого класса проблем, не изменяя рассмотренного в примере выражения, если технические трудности графа уже преодолены.
Что такое параметр?
Однозначно определить параметр довольно сложно. Итак, давайте разберемся, что такое параметр, с помощью 5 фактов.

-
Уравнение \(x^2-a=0\) в разных \(a\) может принимать разную форму:
Я представил лишь несколько общих случаев уравнений и функций. Подставляя другие \(a\) и \(c\), можно получить другие уравнения/функции.
В зависимости от значения параметра меняется количество корней уравнения и сами корни. Аналогично в неравенстве: при разных параметрах будут разные ответы.
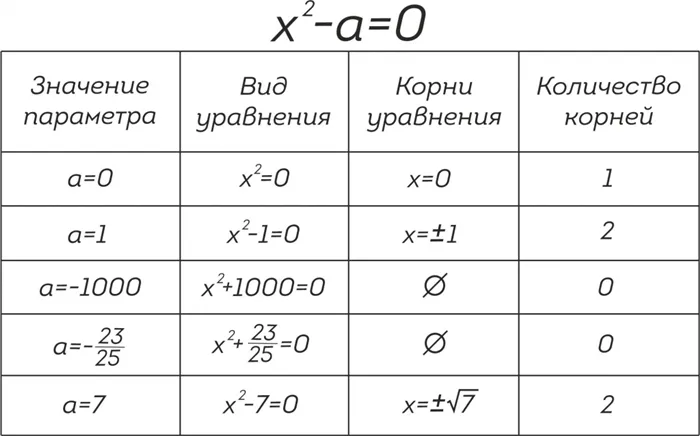

- «при всех a решить уравнение»
- «решить относительно \(x\) уравнение»
- «при всех значениях параметра \(a\) решить неравенство»
- «для каждого значения параметра найти корни» и т.п.
То есть, вы должны рассмотреть все \(a\) возможные варианты и найти решения в каждом случае.
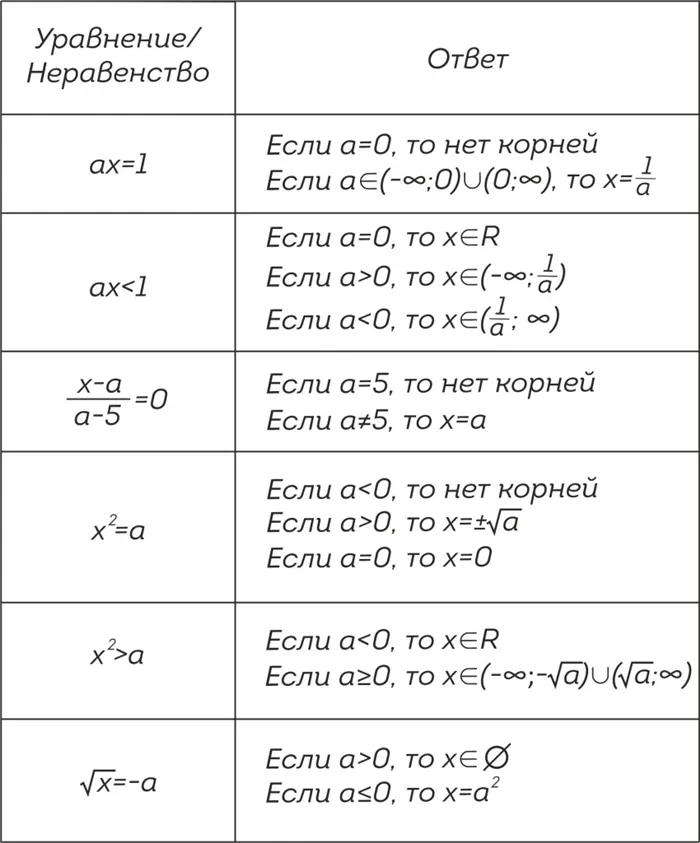
Значение параметра может быть любым, даже запрещенным. То есть, если некоторое значение параметра делает знаменатель равным нулю или подкоренное выражение отрицательным – это значение тоже нужно рассматривать, как и все остальные.
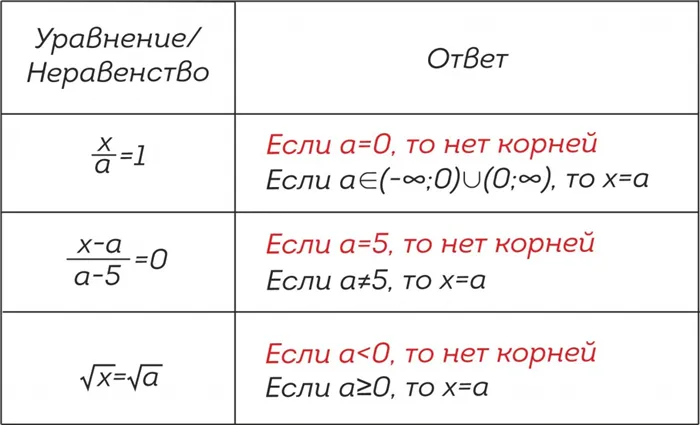
Обратите внимание, что это только один из способов решения уравнения/неравенства с одним параметром. Существуют и другие подходы.
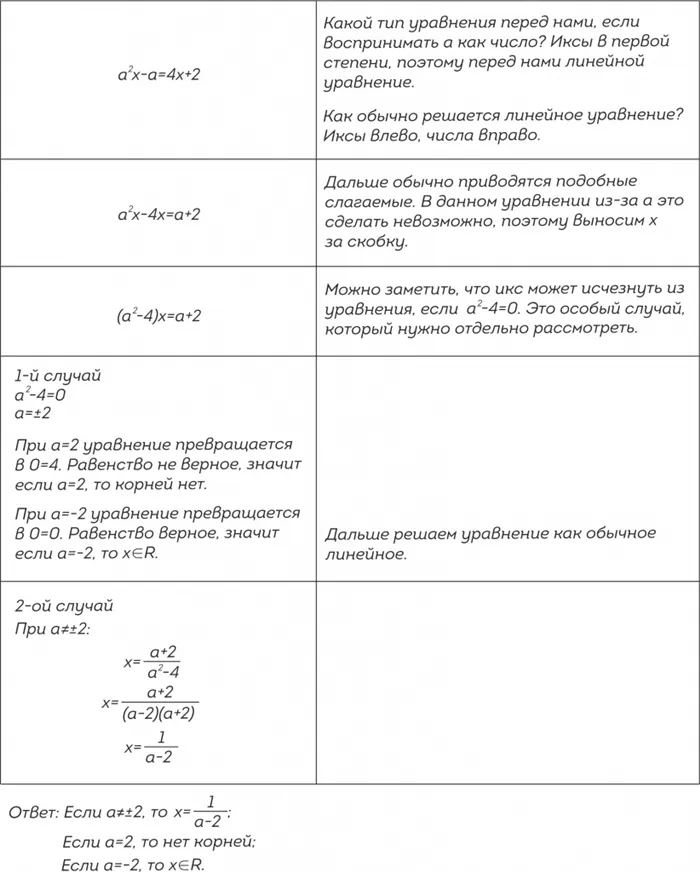
Пример. Решите уравнение \(a^2 x-a=4x+2\).Решить.
Пример. Решить неравенство \(x^2+2ax+4>0\).Решение.
Квадратные уравнения с параметром
Прежде чем приступить к изучению следующего материала, рекомендуем вам ознакомиться с понятием квадратных уравнений в статье Линейные, квадратные и кубические уравнения. Также важно ознакомиться с графиками парабол из статьи Основные элементарные функции.
Квадратичное уравнение имеет вид ax 2 + bx + c = 0, а график функции y = ax 2 + bx + c является параболой.
Как вы можете работать с такими уравнениями, если они содержат параметр? Прежде всего, важна логика. Любая проблема с параметром может быть решена путем анализа функции.
Решение квадратного уравнения основано на понятии дискриминанта. В зависимости от его значений можно получить различное количество корней:
- При D>0 уравнение имеет два корня.
- При D = 0 уравнение имеет один корень.
- При D<0 уравнение не имеет корней.
Как это можно проверить на диаграмме? Корни уравнения — это точки пересечения параболы с осью расстояния, т.е. осью x.
Рассмотрим три уравнения.
1) x 2 — x — 2 = 0 Решим уравнение с помощью силы дискриминанта: D = 1 2 — 4 * 1 * (-2) = 1 + 8 = 9 Поскольку сила дискриминанта больше 0, уравнение имеет два корня.
Давайте проверим это с помощью графика функции. Постройте параболу и отметьте, что она дважды пересекает ось расстояний, координаты этих точек — (-1; 0) и (2; 0).
2) x 2-4x + 4 = 0 Решите уравнение с помощью дискриминанта: D = 16 — 4 * 1 * 4 = 16 — 16 = 0. Поскольку дискриминант равен 0, уравнение имеет только один корень.
Давайте рассмотрим это на диаграмме. Парабола касается оси x только один раз в вершине, координаты которой (2; 0).
3) x 2 — 5x + 7 = 0 Решим уравнение, используя мощность дискриминанта: D = 25 — 4 * 1 * 7 = 25 — 28 = -3
Поскольку дискриминант отрицательный, уравнение не имеет корней. Это становится ясно, когда мы смотрим на график функции: Парабола лежит над осью x и никогда не пересекает ее.
Где мы можем применить эти знания при решении параметров?
Пример 1: Найдите все значения параметра a, при которых уравнение x 2 + (3a + 11)x + 18,25 + a = 0 имеет два различных решения.
Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение имеет два разных корня?
Квадратное уравнение имеет два корня, если D>0. Мы должны найти все значения параметра, для которых дискриминант положителен.
1. сначала нужно найти сам дискриминант.
D = (3a + 11) 2 — 4 * 1 * 1 * (a + 18,25) = 9a 2 + 66a + 121 — 4a — 73 = 9a 2 + 62a + 48
2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a 2 + 62a + 48>0
9a 2 + 62a + 48 = 0 D = 3844 — 1728 = 2116 \(a_1 = \frac = -\frac = -89\) \(a_2 = \frac = -\frac = -6\)
4. дискриминант будет положительным при \(a \in (-\infty; -6)\cup (-\frac; +\infty)\). Вот и ответ.
Ответ.
Это важно: в уравнении мы приводим не решения самого уравнения, а значения параметров, при которых уравнение имеет два решения.
Пример 2: Для каких значений параметра α уравнение (2a + 1)x 2 — ax + 3a + 1 = 0 имеет два различных решения?
Решение. Этот пример похож на предыдущий, но здесь есть важная особенность. Что произойдет с уравнением, если 2a+1 = 0?
Теорема Виета
Дискриминация — не единственный способ решения квадратного уравнения. Обратимся к теореме Вайета. Если дано уравнение ax 2 + bx + c = 0, то корни можно найти по следующей схеме:
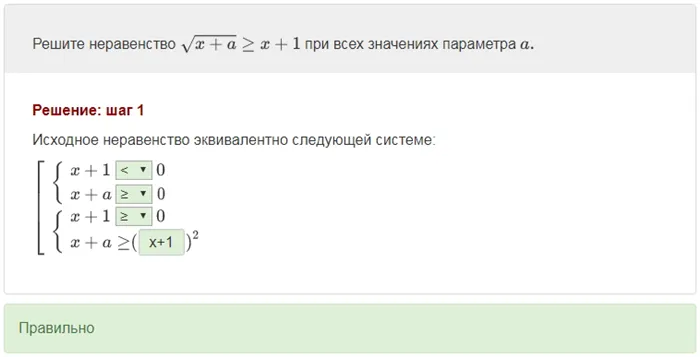
Теорема Виета может быть хорошо применима, если на корни уравнения накладываются дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x 2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1= 5x2.
Решение. 1. корни уравнения — это два разных числа. Следовательно, дискриминант должен быть строго больше 0:
D = 9a 2 — 4 * 1 * (-a 2 + a) = 9a 2 + 4a 2 — 4a = 13a 2 — 4a = a(13a — 4)
Получаем неравенство a(13a — 4)>0, поэтому \(a \in (-\infty; 0) \cup (\frac; +\infty)\).
Найдите корни уравнения, используя теорему Виета. 5:
5. найти значения параметра, для которых условие выполняется. Остается проверить, что для этих значений уравнение имеет два корня.
a = 0 не подходит, потому что условие \(a \in (-\infty; 0) \cup (\frac; +\infty)\) не включает точку 0.
\(a = \frac\) подходит, поскольку \(\frac>\frac).
Реакция.
Условия на корни квадратного трехчлена
Однако возможны и более сложные назначения параметров. Давайте рассмотрим каждый из этих случаев.
1. корни квадратичного тринома меньше числа N.
Мы хотим построить параболу. Напомним, что ножки параболы могут быть как вверх, так и вниз.
Если ножки параболы направлены вверх. Отметьте точку N на оси x так, чтобы она находилась справа от двух корней уравнения. Это ставит условие, чтобы корни уравнения были меньше числа N.
Предположим, мы идем по холмистой местности и имеем ее карту. Если перед нами плоская картина, мы можем понять, как точки расположены в пространстве по отношению друг к другу. Однако если мы посмотрим на землю сбоку, то увидим, что точки находятся на разной высоте.
Предположим, что точки пересечения параболы с осью x являются точками покоя на прямой, а в точке N находится смотровая площадка.
Что вы можете сказать о смотровой площадке на этой карте? Она находится выше других точек и расположена справа от самой низкой точки на земле.
Представьте эти условия на диаграмме. В точке N значение функции f(x) больше корня уравнения. Она также находится справа от вершины параболы, т.е. ее наклон больше, чем наклон параболы.
Почему эти условия так важны? Предположим, что точка N находится слева от вершины параболы. Тогда условие, что корней меньше N, не выполняется.
В этом случае точка обзора на нашем экскурсионном маршруте находится перед зоной отдыха.
Что если значение функции в точке N меньше корня уравнения? Точка N будет находиться между ними.
В этом случае смотровая площадка будет находиться между местами отдыха.
Аналогично можно наблюдать изменение условий при любом положении точки N на диаграмме.
Для того чтобы оба корня квадратичного тринома ax 2 + bx + c были меньше числа N, необходимы и достаточны следующие условия:
Что произойдет, если ветви параболы будут направлены вниз? Наш маршрут немного изменится: вместо оврага будет гора.
Где сейчас находится смотровая площадка? Он будет находиться ниже павильонов и дальше от самой высокой точки горы.
Из этого можно сделать вывод, что точка N на графике находится справа от вершины параболы и значение функции там меньше, чем значение функции у корней уравнения.
Для того чтобы оба корня квадратичного тринома ax 2 + bx + c были меньше числа N, необходимы и достаточны следующие условия:
2. корни квадратичного тринома больше числа N.
Мы рассуждаем так же, как и для предыдущей функции, но теперь N смещено в левую часть параболы.
Если ножки параболы направлены вверх, то функция принимает большее значение в точке N, чем в корнях уравнения, а сама N лежит слева от параболы.
Для того чтобы оба корня квадратичного тринома ax 2 + bx + c были больше числа N, необходимы и достаточны следующие условия:
Теперь выведем ветви параболы вниз. Значение функции в точке N меньше корня уравнения.
Для того чтобы оба корня квадратичного тринома ax 2 + bx + c были больше числа N, необходимы и достаточны следующие условия:
Анализируя положение точек на графике функции, можно определить условия для каждого условия, даже если точек много.
Развитие у учащихся умений моделирования при решении задач с параметрами

Понятие параметра тесно связано с понятием переменной. Переменная — это величина, которая может принимать различные значения. Введение переменной величины в математику в 17 веке — это революционный скачок в развитии науки в целом. Она ознаменовала новый этап в понимании природных явлений в их взаимосвязи и движении. Начиная с декартовой переменной, было разработано понятие функции.
Таким образом, переменная — это общий термин для обозначения различных, изменяющихся величин.
Параметр — это вспомогательная переменная, которая включается в формулы и выражения. Обычно параметр — это скалярная величина или вещественное число; параметр обозначается буквой алфавита. Часто параметр также рассматривается как постоянное число в условиях конкретной задачи, но как переменная в другой задаче.
1. в квадратном уравнении коэффициенты являются параметрами, x — переменной. При решении уравнения коэффициенты рассматриваются как фиксированные числа, но в общем случае их можно рассматривать и как переменные.
2. уравнение в декартовой прямоугольной системе координат является уравнением множества окружностей единичного радиуса; номера и параметры окружности в рассматриваемом множестве; подставляя, получаем вполне определенную окружность с центром в точке (1; 3) единичного радиуса из множества окружностей того же радиуса.
В задачах есть 2 типа символов: неизвестные переменные (обозначаются ) и параметры. Разница между ними весьма условна, и можно считать, что параметр — это переменная, значение которой предполагается постоянным, и что любое значение параметра в терминах неизвестного определяет соответствующее уравнение (неравенство, систему, функцию).
Употребление букв в математике
Поскольку буквы широко используются в математике, необходимо знать их различные функции.
Первая функция — это декларативная функция, где буква обозначает либо любое число из заданного множества, либо даже выражение, точку, линию, фигуру и т.д.
Прописные или строчные буквы M, N, K, .
Например, буквы используются для записи закона чередования:, где буквы в обозначениях означают любые числа. В обозначениях a|||b буквы обозначают прямые линии. MN — это линия (радиус, отрезок). M знак (количества, числа, выражения), это обозначение конкретного числа.
Вторая функция — это обобщающая функция, где буква служит обобщением возможных значений величины, коэффициента и т.д.. В этом случае такая буква называется параметром.
Для обозначения параметров обычно используются первые строчные буквы алфавита. Так, в уравнении ax + b = c буквы a, b и c являются параметрами.
Третья функция является функцией запроса, если мы хотим найти значения этих букв, для которых выполняются условия, указанные в задании. В данном случае эти буквы представляют собой неизвестные (искомые) значения задачи.
Для неизвестных величин используются строчные буквы алфавита x, y, z ,. или стандартные символы для соответствующих величин: Путь — s, S- Время — t, T- Скорость — и т.д.
Параметры алгебра — объясните,что такое параметр в заданиях по алгебре в 9,10 классе? — 22 ответа
что такое параметр в алгебре
Научная часть на вопрос «Что такое параметр в упражнениях по алгебре в 9, 10 классе?» по Уоррену лучший ответ это параметр — это конкретное число или набор чисел, которые удовлетворяют определенным условиям
Ответ от 22 гуру
Здравствуйте. Вот подборка тем с ответами на ваш вопрос: объясните, что такое параметр в упражнениях по алгебре за 9, 10 класс.
Ответ spathi guru Просто неизвестное, которое нужно найти, чтобы оно удовлетворяло определенному условию, в вашем случае, например, что оно имеет три корня.
Ответ от spathi guru Да, только вторая переменная. Он называется параметром, потому что его значение обычно сначала нужно найти. По сути, переменная и параметр — это одно и то же, только здесь основное внимание уделяется поиску только значений параметра. То есть вы должны составить систему уравнений и/или неравенств, в которой есть этот параметр. Думаю, вы уже догадались, что для выполнения условий в этом уравнении один дискриминант должен быть равен нулю, а второй — больше нуля (или наоборот). Переменная x больше не нужна при записи дискриминантных сил.
Ответ Dvutavorny novik Там нужно 3 корня, а график (каким бы ни был a) имеет только 2 точки, где y=0, поэтому максимальное количество корней — 2, не может быть 3. В целом, лучше всего использовать следующее решение: — Постройте график — Проанализируйте — Выберите точку (где y=a) в Ox, где y=0 — Запишите ответ. Поправьте, если вы ошибаетесь.
Ответ от гуру ответа 2
Здравствуйте. Вот еще темы с правильными ответами:
Параметры в Википедии Поиск статьи Параметры в Википедии.
Найдите статью Эпистаз в Википедии.
Ответить на вопрос:
Что такое параметры в математике
Величина, используемая для количественного описания характеристик или свойств объектов; в математике она может быть фиксированной или переменной. Если я правильно помню. И вообще, многие ученые интерпретируют его так, как им удобно его представлять.
Это количество, которое может быть использовано для создания любой функции
Это число (константа), обозначаемое буквой. Обычно неизвестные обозначаются буквами X, Y, Z, а параметры — a, b, c.
Постараюсь обойтись без пространных рассуждений. Приведу конкретный пример. Рассмотрим простейшее уравнение: 2х + 3 = 7. Очевидно, оно имеет один корень: х=2. Рассмотрим похожее уравнение aх + 3 = 7. Попробуем решить его относительно х. Можно ли утверждать, что его решением будет х = 4/a? Категорически нет! Мы решали параметрическое уравнение по тому же принципу, что и «обычное» =>Вы правильно ответили «не совсем». Теперь попробуйте найти, где была допущена ошибка. Каким должен быть правильный ответ?








