В психотерапии парадокс, то есть следующие парадоксальные методы, используется для лечения многих проблем. Каждый метод интересен по-своему, поэтому давайте остановимся на нем подробнее.
Что означает слово парадокс?
Парадокс (от древнегреческого (paradoxos) paradoxos — неожиданный — странный + от древнегреческого para-dodeo — казаться) — Оригинальное мнение, которое на первый взгляд не соответствует истине, но которое после тщательного изучения оказывается верным (Словарь иностранных слов, 1912) — Своеобразное мнение, сильно расходящееся с общепринятым, противоречащее (иногда только внешне) здравому смыслу (Словарь иностранных слов, 1954) — Мнение, суждение, сильно расходящееся с общепринятым, противоречащий здравому смыслу (Словарь иностранных слов, 1979) — своеобразное, неожиданное суждение, которое сильно расходится с общепринятым мнением и иногда только кажется противоречащим здравому смыслу (Словарь литературных терминов, 1955) — положение дел (утверждение, тезис, суждение или вывод), которое может существовать в действительности, но не имеет логического объяснения (Википедия) — Неожиданный, утверждение, тезис, суждение или вывод, который может существовать в действительности, но не имеет логического объяснения (Википедия)
Традиция — Неожиданный, необычный, непривычный, оригинальный, противоречащий самому себе, первоначальному предположению, общепринятому традиционному мнению или здравому смыслу.
Парадоксы Марка Твена

«Не откладывай на завтра то, что можно отложить на послезавтра». «Бросить курить легко, я делал это тысячу раз». «Лучше молчать и выглядеть глупо, чем открыть рот и устранить все сомнения. «Если вы оказались на стороне большинства, это верный признак того, что пришло время меняться.
Парадоксы Михаила Жванецкого

М. Жванецкий

Оскар Уайльд
«Истина нашей жизни раскрывается именно в форме парадоксов. Чтобы понять реальность, нужно увидеть, как она балансирует на канате» (Оскар Уайльд, «Портрет Дориана Грея»).
Парадокс: разбор понятия

Многие считают, что парадокс — это продукт философской мысли, игра логики, но он возникает и в прикладной науке по мере ее развития. Первоначально явления понимаются исследователями упрощенно. Со временем ученые сталкиваются с необъяснимыми фактами. Это приводит к противоречию между старыми и новыми знаниями.
До Великой депрессии считалось, что если люди будут экономить, то рецессии не будет. Однако опыт изучения финансовых кризисов позволяет сделать вывод, что уменьшение расходов ведет к снижению потребительского спроса и уменьшению заработной платы. Это приводит к парадоксу: чем больше мы экономим, тем беднее становимся.
Парадокс и логика
Древнегреческие философы часто отмечали противоречия между логикой и рассуждениями, которые приводили к взаимоисключающим выводам. Этот парадокс объясняется нечетким определением понятий или объектов.
Апория и антиномия
В логике существует два типа противоречий:
Выдуманное, но логически верное заключение называется вопросом. Парадокс основан на несовместимости факта с его объяснением. Самый известный вопрос — это вопрос древнегреческого философа Зенона Энейского.
Антиномия в переводе с древнегреческого означает «противоречие в законе». Это существование двух взаимоисключающих, но логически доказуемых суждений.
Парадокс: логический
Чтобы понять суть термина парадокс, необходимо привести несколько примеров, что мы и сделаем. Чаще всего известные парадоксы связаны с древнегреческими героями из мифов.
Ахиллес и черепаха
Самый известный вопрос Зенона. Бегун Ахилл решил состязаться с черепахой и дал ей фору в 500 метров. Пройдя это расстояние, он обнаружил, что черепаха прошла небольшое расстояние и опередила его. Он снова попытался догнать ее, но черепаха тем временем ушла вперед.
Сколько бы Ахилл ни приближался к черепахе, она не отходила от него ни на шаг. Парадокс заключается в том, что Ахиллес никогда не догонит черепаху.
Летящая стрела — еще один парадокс. Летящая стрела всегда покоится, т.е. она всегда находится в состоянии покоя и никуда не летит.
Парадокс лжеца
Самый известный пример антиномии. Эпименид с Крита говорил: «Все критяне — лжецы». Если Эпименид лжец, то его утверждение ложно, а жители Крита не лжецы. Таким образом, Эпименид тоже не лжец, но если он говорит правду, то критяне — лжецы, включая самого Эпименида. Парадокс заключается в том, что суждения в обоих случаях являются логически истинными, но взаимоисключающими.
Парадокс о всемогуществе
Бог всемогущ. Способен ли он создать камень, который не может поднять? Если да, то он теряет свое всемогущество, а если нет, то Бог не всемогущ.
Парадокс и софизмы
Софизм (греч. sophism (sofima) — хитрость, загадка) — это ложное утверждение с ошибкой в рассуждениях. Таким образом, софисты специально совершили ошибку. Они пытались запутать своего оппонента и выиграть спор.
Софизмы использовались в логике, риторике, философии, математике и физике.
Примеры софизмов
Если стакан наполовину пуст, значит, он наполовину полон. А если половины равны друг другу, то и целое также равно друг другу. Получается, что пустой = полный.
Другим примером софистики может служить распространенная софистика о рогах. «Если вы не потеряли что-то, значит, вы что-то потеряли. Если вы не потеряли свои рога, значит, у вас есть рога».
Обе софистики основаны на формуле A = B, B = C или C = A. Но это математическое равенство не всегда работает в случае логики.
В случае с первой софистикой имеет место ошибка в мышлении. Полупустой — не значит наполовину пустой. Наполовину пустой — это только наполовину полный. Поэтому нельзя отождествлять пустоту с полнотой.
Ошибка во второй софистике заключается в том, что рога не ваши. К этому «чему-то», что вы не потеряли и что у вас есть, рога не относятся. Поэтому их нельзя отнести к «чему-то». Следовательно, второе предложение ложно.
Парадокс и апория
Извинения (образованные от греческого слова apologia — бедствие, безвыходная ситуация) — это всегда воображаемые ситуации, которые невозможно разрешить.
В таких ситуациях наши эмпирические знания сталкиваются со знаниями, которые мы получаем в результате анализа ситуации. Вопросы используются в логике и риторике.
Парадокс описывает ситуации, которые могут возникнуть в реальности.
Примеры логических апорий
Самым известным философом, чье имя связано с этим вопросом, был древнегреческий философ Зенон Аэлийский. «Ахиллес и черепаха» — одна из теорем Зенона.
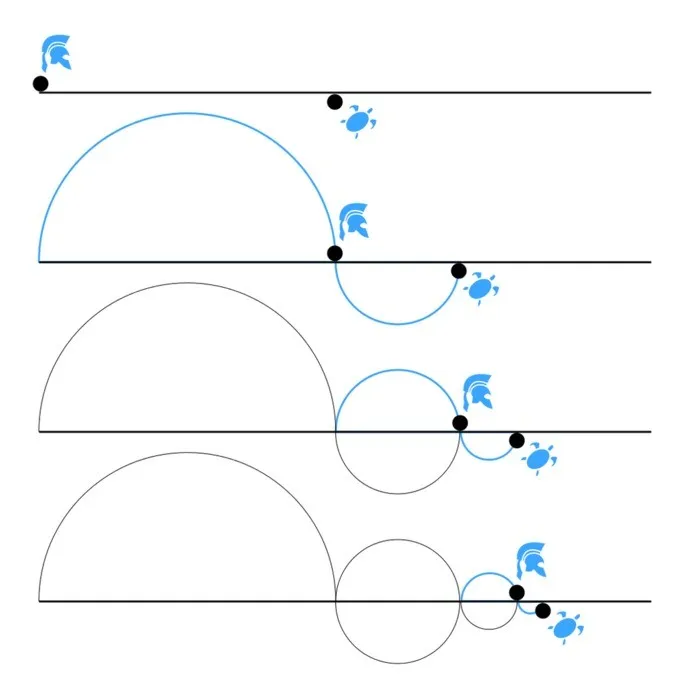
Согласно этому чуду, Ахиллес не может догнать черепаху, если черепаха начнет двигаться впереди Ахиллеса.
Пока Ахиллес преодолевает расстояние, которое прошла черепаха, черепаха идет все дальше и дальше.
Например, пока Ахиллес делает 10 шагов, черепаха успевает сделать 9 шагов. Ахиллес делает 9 шагов, черепаха — 8. И так до бесконечности.
Примеры апорий в риторике
В риторике вопрос — это намеренное высказывание, выражающее сомнение или вопрос. Как правило, вопрос используется в форме риторического вопроса.
Этот метод используется для того, чтобы заставить собеседника поверить, что вы не знаете или не можете знать ответ на вопрос.
«Разве это не удовольствие, — сказал Кандид, — критиковать все и находить недостатки там, где другие видят только красоту? Кандид Вольтера или оптимизм * Перевод.
Антиномия
Антиномия (от греческого antinomia противоречие в законе) — это два утверждения, которые не согласуются друг с другом и не допускают друг друга, но каждое из них может быть обосновано.
Это считается разновидностью парадокса. Некоторые ученые даже считают антиномию и логический парадокс одним и тем же.
Антиномия отличается от софизма тем, что в ней нет ошибок в расчетах или логических рассуждениях. Он состоит из утверждений, которые являются взаимоисключающими.
Поэтому парадокс «лжеца» Эввулида считается антиномией. Ибо в нем содержится противоречие: нужно лгать и говорить правду одновременно. Это невозможно.
Другой пример — логический парадокс цирюльника. Это звучит примерно так: Парикмахер бреет только тех, кто не бреется сам. Может ли парикмахер сам себя побрить?
Если парикмахер не бреется сам, он может побрить себя сам. Но если он бреется сам, значит, он уже нарушил правило не бриться, чтобы парикмахер мог побрить вас.
Эти утверждения связаны между собой, но в то же время они исключают и отрицают друг друга. Это противоречие.
Антиномия чистого разума
Немецкий философ Иммануил Кант ввел понятие антиномии чистого разума. Он подразумевал, что в этом состоянии чистого разума человек разделен, и законы, по которым он живет, противоречат друг другу.
12 невероятных парадоксов

Невероятные факты
Парадоксы существуют со времен древних греков. С помощью логики можно быстро найти фатальный изъян в парадоксе, который покажет, почему кажущееся невозможным возможно или что весь парадокс просто основан на ошибках в мышлении.
Можете ли вы определить, в чем заключается недостаток каждого из следующих парадоксов?
Парадоксы пространства
12. парадокс Ольберса
В астрофизике и физической космологии парадокс Ольберса — это аргумент о том, что темнота ночного неба противоречит предположению о бесконечной и вечной статичной Вселенной. Это ссылка на нестатичную вселенную, подобную современной модели Большого взрыва. Этот аргумент часто называют «темным парадоксом ночного неба», который гласит, что при любом угле обзора с Земли линия зрения заканчивается, когда она достигает звезды.

© snezhanna / Getty Images
Чтобы понять это, давайте сравним парадокс с поиском человека в лесу среди белых деревьев. Если линия зрения из любой точки заканчивается на верхушках деревьев, продолжает ли человек видеть только белый цвет? Это контрастирует с темнотой ночного неба и заставляет многих людей задаваться вопросом, почему мы не видим в ночном небе только свет звезд.
11 Парадокс всемогущества
Парадокс заключается в том, что существо, которое может выполнить любое действие, может ограничить свою способность выполнять его, поэтому оно не может выполнять все действия, но, с другой стороны, если оно не может ограничить свои действия, то это то, что оно не может делать.
Это, похоже, подразумевает, что способность всемогущего существа ограничивать себя обязательно означает, что оно само себя ограничивает. Этот парадокс часто выражается в терминологии авраамических религий, хотя это не является обязательным условием.

Вариантом парадокса всемогущества является так называемый парадокс камня: может ли всемогущее существо создать камень, который настолько тяжел, что оно само не может его поднять? Если да, то существо больше не всемогуще, а если нет, то существо изначально не было всемогущим.
Ответ на парадокс таков: наличие слабости, например, неспособность поднять тяжелый камень, не подпадает под категорию всемогущества, хотя определение всемогущества подразумевает отсутствие слабостей.
10. парадокс сориты
Парадокс заключается в следующем: Представьте себе кучу песка, из которой постепенно удаляются песчинки. Мы можем построить силлогизм на основе этих утверждений:
— 1000000 песчинок — это куча песка.
— Куча песка без единой песчинки все равно остается кучей песка.

© ninoninos / Getty Images
Если вы продолжите второе действие без остановки, то в итоге получите кучу, состоящую из одной песчинки. На первый взгляд, есть несколько способов избежать этого вывода. Против первой предпосылки можно возразить, что миллион песчинок — это не куча. Однако вместо 1000000 может стоять любое другое большое число, и тогда второе предложение применимо к любому числу с любым количеством нулей.
Поэтому ответ должен однозначно отрицать существование таких вещей, как куча. В качестве альтернативы можно возразить против второй посылки, что она не применима ко всем «коллекциям зерен» и что при удалении одной песчинки или песка остается куча. Или он может утверждать, что куча песка может состоять из одной песчинки.
Софизм «Крокодил»
Мать и ее ребенок стоят на берегу реки. Вдруг подплывает крокодил и утаскивает ребенка в воду. Отчаявшаяся мать просит вернуть ей ребенка, и крокодил отвечает, что отдаст его ей невредимым, если женщина правильно ответит на вопрос «Вернет ли он ей ребенка?». У женщины явно есть два варианта — «да» или «нет». Если она скажет, что крокодил отдаст ей ребенка, все зависит от животного — если ответ будет правдивым, похитительница отпустит ребенка, но если она скажет, что мать ошибается, она не получит ребенка, согласно всем правилам договора.

Отрицательный ответ женщины значительно усложняет ситуацию — если он правдив, похититель должен выполнить соглашение и освободить ребенка, но в этом случае ответ матери не будет правдивым. Крокодил должен вернуть ребенка матери, чтобы убедиться, что этот ответ ложный, но это противоречит соглашению, потому что ее ошибка должна оставить ребенка с крокодилом.
Следует отметить, что соглашение крокодила содержит логическое противоречие, поэтому его обещание не может быть выполнено. Автором этого классического софизма считается оратор, мыслитель и политик Коракс из Сиракуз, живший в пятом веке до нашей эры.
Апория «Дихотомия»
Еще один парадокс Зенона Элевтерского, который показывает неточность идеализированной математической модели движения. Проблема может быть сформулирована следующим образом: Предположим, вы поставили себе цель пройти по одной из улиц вашего города от начала до конца. Другими словами, вы проходите половину общего расстояния, затем четверть, восьмую часть, шестнадцатую — количество сокращающихся сегментов пути стремится к бесконечности, поскольку каждый оставшийся сегмент можно разделить на две части, что делает невозможным прохождение всего расстояния. Сформулировав этот несколько надуманный парадокс, Зенон хотел показать, что математические законы противоречат действительности, поскольку в реальности можно легко пройти все расстояние без остатка.
Знаменитый парадокс Зенона Свободного затрагивает самые глубокие противоречия в представлениях ученых о природе движения и времени. Вопрос формулируется следующим образом: Стрела, выпущенная из лука, останавливается, потому что она все время находится в состоянии покоя, не двигаясь. Если стрела находится в покое в любой момент времени, то она всегда находится в покое и не движется, потому что не существует времени, в которое стрела перемещается в пространстве.
Самые выдающиеся умы человечества веками пытались разгадать парадокс летящей стрелы, но с логической точки зрения он абсолютно верен. Чтобы опровергнуть его, нужно объяснить, как конечный промежуток времени может состоять из бесконечного числа мгновений — даже Аристотель, который убедительно критиковал вопрос Зенона, не смог этого доказать. Аристотель справедливо указывал, что время нельзя рассматривать как сумму отдельных неделимых мгновений, но многие ученые считают, что его подход не очень глубокий и не опровергает существование парадокса. Стоит отметить, что в задаче о летящей стреле Зенон не пытался опровергнуть возможность движения как такового, а указывал на противоречия в идеалистических математических концепциях.
Парадокс Галилея

В своей работе «Рассуждения и математические доказательства о двух новых отраслях науки» Галилео Галилей предложил парадокс, доказывающий странные свойства бесконечного множества. Он сделал два противоречивых заявления. Во-первых, есть числа, которые являются квадратами других целых чисел, например, 1, 9, 16, 25, 36 и т.д. Есть и другие числа, которые не обладают этим свойством — 2, 3, 5, 6, 7, 8, 10 и т.д. Поэтому общее количество точных квадратов и обычных чисел должно быть больше, чем количество точных квадратов. Второе суждение: для каждого натурального числа найден его точный квадрат и для каждого квадрата существует целый квадратный корень, т.е. количество квадратов равно количеству натуральных чисел.
Из-за этого противоречия Галилей сделал вывод, что силлогизм о количестве элементов применим только к конечным множествам, хотя позже математики ввели понятие мощности множества — с его помощью было показано, что второе суждение Галилея применимо и к бесконечным множествам.
Дилемма крокодила

Разновидность парадокса лжеца, распространенная древнегреческим философом Эввулидисом. «Дилемма крокодила развивалась следующим образом. Крокодил крадет ребенка у своего родителя и говорит родителю, что вернет ребенка, если родитель правильно угадает, вернет крокодил ребенка или нет. Если родитель говорит: «Ты вернешь моего ребенка», то все в порядке, и ребенок возвращается. Но если родители говорят: «Вы не вернете моего ребенка», то это парадокс.
Парадокс заключается в том, что когда крокодил возвращает ребенка, он нарушает свое слово, потому что родители не догадались. Однако если крокодил не вернет ребенка, он также нарушит свое слово, потому что родители были неправы. Очевидно, что ребенку суждено остаться в пасти крокодила, потому что пара никогда не придет к соглашению. Псевдорешение этого парадокса заключается в том, чтобы тайно сообщить третьей стороне об истинных намерениях крокодила. Тогда крокодил выполнит свое обещание независимо от ответа.
Парадокс слабого молодого Солнца

Этот астрофизический парадокс возник, когда мы поняли, что наше Солнце почти на 40% ярче, чем было почти четыре миллиарда лет назад. Однако, если бы это было так, Земля должна была получать гораздо меньше тепла в прошлом, что означает, что поверхность планеты замерзла бы. Парадокс слабого молодого солнца, впервые поднятый ученым Карлом Саганом в 1972 году, озадачил все научное сообщество, поскольку геологические данные показывают, что наша планета почти всегда была покрыта океанами.
В качестве одного из возможных решений были предложены парниковые газы. Но их уровень должен быть в сотни или тысячи раз выше, чем сейчас. Более того, существует множество доказательств того, что это не так. Возможно, свою роль сыграла некая «планетарная эволюция». Согласно этой теории, условия на Земле (например, химический состав атмосферы) менялись по мере эволюции жизни.
Парадокс Гемпеля

Парадокс Геббельса, также известный как «парадокс ворона», — это вопрос о природе доказательств. Она начинается с утверждения «все вороны черные» и логического контраргумента «все, что не черное, не ворона». Затем философ утверждает, что всякий раз, когда мы видим ворону — а все вороны черные — первое утверждение доказано. Когда мы видим нечерный объект, например, зеленое яблоко, второе утверждение подтверждается.
Парадокс возникает потому, что каждое зеленое яблоко также доказывает, что все вороны черные, поскольку эти две гипотезы логически эквивалентны. Наиболее распространенным «решением» проблемы было бы согласиться с тем, что каждое зеленое яблоко (или белый лебедь) является доказательством того, что все вороны черные, но с оговоркой, что количество доказательств настолько мало, что они становятся несущественными.








