Что такое линия в геометрии. Что такое линия в геометрии.

Основными фигурами на плоскости являются точка и линия. Точки обычно обозначаются заглавными буквами — A, B, C, D. Линии обозначаются строчными буквами — a, b, c, d. (Рисунок 1).

Прямые, кривые и очень изломанные. Краткая история линии от «Начал» Евклида до фракталов начала XX века

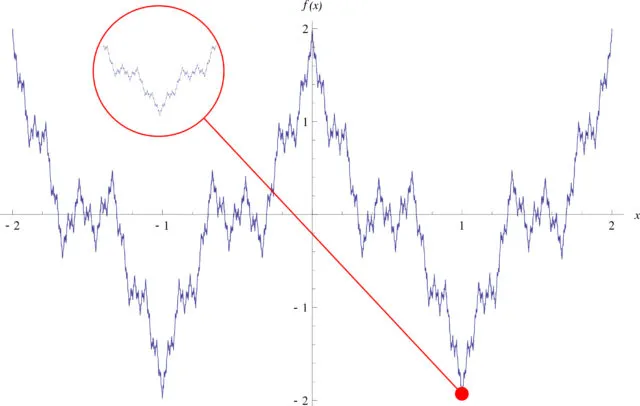
Что такое линия? В чем разница между различными кривыми? Математики задаются этими вопросами уже 2500 лет, и путь к ответам на них не был лишен драматизма — открытие иррациональных отрезков прямых, согласно легенде, стало трагедией для пифагорейцев, а открытие заполняющих площадь кривых Пеано в начале 20 в. Математик и художник Дэвид Кац об истории понятия «кривые» в древней и средневековой математике и в современном математическом анализе.

Интерес человека к прямым и кривым линиям прослеживается с древности. Мы видим всевозможные кривые в геометрических узорах в керамике и архитектуре. Помимо довольно простых узоров, состоящих из прямых линий, часто встречаются и более сложные: спирали, волнистые линии и многое другое.

Концепции геометрии уже существовали в Египте и в цивилизациях Плодородного полумесяца. Очевидно, они возникли из очень практических потребностей: например, для сельского хозяйства было важно иметь возможность измерять площадь земли. Однако в сохранившихся источниках мы находим эти понятия скорее как набор рецептов, чем как науку.

Греция: длина без ширины

Древние греки придерживались более строгого подхода. В «Элементах» Евклида мы находим определения (хотя часто довольно описательные — далее они, например, не упоминаются) линии, прямой, точки. Они, мягко говоря, выглядят устаревшими:

Определение 1.1 Точка — это место, где ничего нет.

Определение 1.2 Линия — это длина без ширины.

Определение 1.3 Концы прямых являются точками.

Определение 1.4 Прямая линия лежит равномерно относительно точек, лежащих на ней. (Или: Прямая линия — это линия, которая лежит одинаково во всех точках).

Первое из этих определений можно интерпретировать в терминах теории множеств, если хотите; третье, похоже, подразумевает, что наши линии конечны априори. Второе можно интерпретировать описательно, в то время как мнения по поводу четвертого сильно расходятся.

Несколько иная, хотя местами схожая, ситуация возникает в работе, традиционно приписываемой Герону, «Определение понятий геометрии» (но в W. R. Knorr, «Arithmêtikê stoicheiôsis: on Diophantus and Hero of Alexandria, Historia Math. 20 (2) (1993), 180-192):

Вот еще несколько примеров, которые были известны грекам.

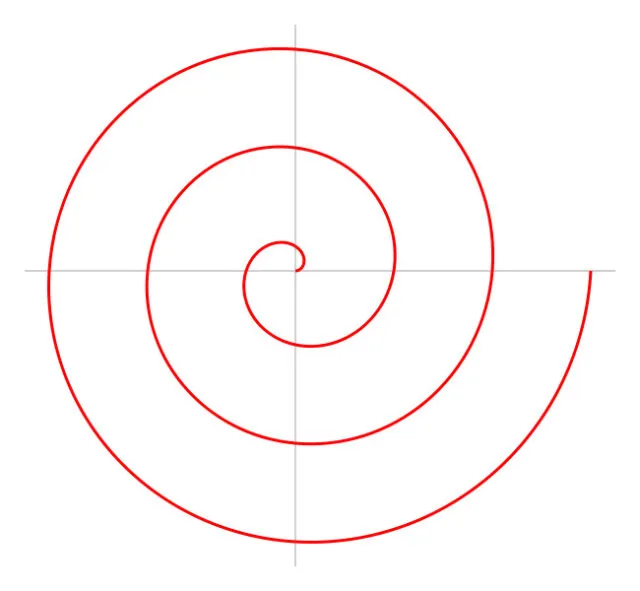
Знаменитая спираль Архимеда:

Вторжение иррационального

Кстати, у греков уже были проблемы с отрезками и линиями. Давайте пройдем этот путь вместе с ними. Возьмите квадрат со стороной 1 и, используя теорему Пифагора, вычислите, что его диагональ равна квадратному корню из двух. Мы сразу оказываемся в затруднительном положении: корень из двух (как мы теперь знаем) иррационален, а это значит, что если уменьшить сторону квадрата целое число раз, то из получившихся частей нельзя получить диагональ: Она будет либо немного больше, либо немного меньше. Можно было бы указать здесь на неточность вычислений или измерений, но пифагорейцы пришли к этому результату вовсе не на практике, а на теоретических основаниях. Их доказательство было следующим:

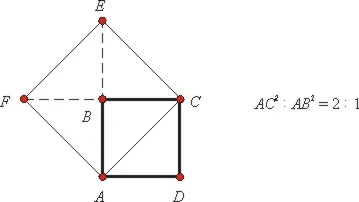
Согласно теореме Пифагора, площадь квадрата со стороной AC в два раза больше площади квадрата ABCD, т.е. m 2 = 2 n 2. Пусть 2 N равно 2 N. Тогда m 2 = 4 N 2. Поскольку 4 N 2 = 2 n 2, n 2 = 2 N 2. Поэтому n также является четным числом. Это противоречит предположению, что одно из чисел m и n нечетное.

Это была неприятная новость для пифагорейцев — в арифметике они не сталкивались с такими числами, и поэтому казалось, что вычисления длины в целом также находятся в затруднительном положении.

Интересно, что позднее, в рукописи «Выпрямление кривой» (для целей нашей статьи это чрезвычайно интересное название — позже мы увидим, почему) некоего Альфонса, вероятно, крещеного еврея, жившего в Испании между XIII и XV веками, отношение к чрезмерной длине уже гораздо более дружелюбное:

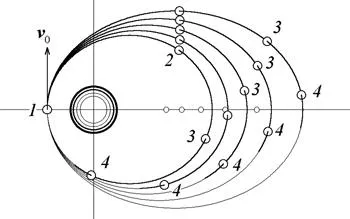
В предыдущих шагах было сформулировано понятие алгебраической кривой — совокупности точек, координаты которых связаны уравнением кривой.

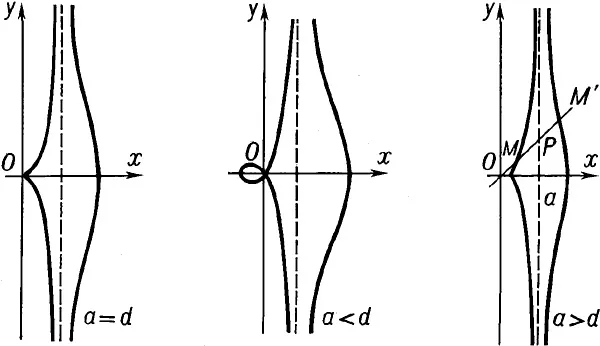
Интересно, что уже на этом алгебраическом уровне возникают кривые со странными особенностями. Возьмем, к примеру, гиперболу — график функции 1/x, с которым многие знакомы еще со школы. Его можно нарисовать с помощью точек, но легко увидеть, что уравнение y = 1/x имеет решение для каждого x, кроме одного: x = 0 (оно не может делиться на ноль). Это также влияет на график:

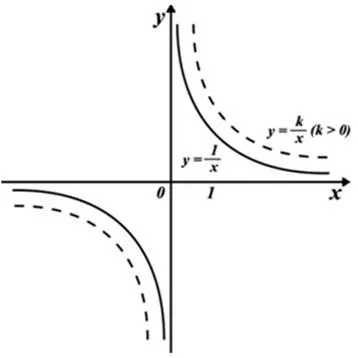
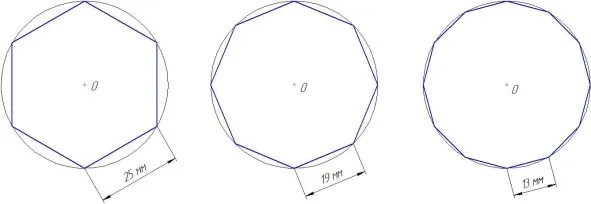
Для простых примеров — например, окружностей, синусоид, парабол — этот подход работает идеально. Примеры неудач такого подхода обсуждаются ниже.

Кривизна плоской кривой

Значение угла α° между полукругами в двух бесконечно близких точках, деленное на длину дуги s, заключенной между этими точками, характеризует кривизну линии.

На рисунке 100 показано, что окружность кривизны в точке приближения имеет общую с кривой l касательную tA и нормаль nA. Благодаря этому свойству центр кривизны кривой в определенной точке может быть определен графически.

Эволюта и эвольвента

Определение эволюции и спиральности неотделимо от кривизны кривой. Если определить положение центров кривизны O1, O2, …, Op ряда, принадлежащего кривой l (рис. 102), точки A1, A2, …, Ap, и соединить их плавной кривой, то получится кривая m, которая называется кривой эволюции кривой l. Таким образом, эвольвента — это множество точек, которые являются центрами кривизны линии.

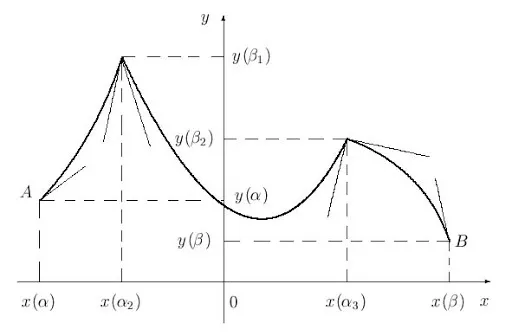
Форма кривой l вблизи точки M с простой касательной t зависит от пути движения точки по касательной и направления вращения касательной. Проиллюстрируем это утверждение примерами.Читать далее

Ортогональные проекции линии

Чтобы построить ортогональные проекции кривой (пространственной или плоской), нужно построить проекции некоторых точек, принадлежащих этой кривой, и соединить проекции с тем же именем в том же порядке, в каком они были в оригинале.

На рисунке 114 мы видим две проекции пространственной кривой l. Чтобы определить длину кривой, нужно ее выпрямить. Выравнивание пространственной кривой, заданной ортогональными проекциями, осуществляется следующим образом:Читать далее

Признаки равенства треугольников:

1. Треугольники равны по двум сторонам и углу между ними

1. Треугольники равны по стороне и двум прилежащим к ней углам

1. Треугольники равны по трём сторонам

Теперь давайте разберемся, что означает сходство:

Если треугольники похожи, но отличаются только размером, то сходство треугольников помогает

Коэффициент подобия — это число, на которое отличаются стороны треугольников

Если ABC похож на A1B1C1, то выполняется равенство, где k — коэффициент сходства.

Если треугольники подобны, то отношение их площадей равно квадрату коэффициента подобия

Признаки подобия треугольников:

Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы, входящие между этими сторонами, равны, то эти треугольники подобны.

1. По двум углам

Если два угла треугольника равны двум углам другого треугольника, то эти треугольники подобны.

1. По трём сторонам

Если стороны треугольника равны сторонам другого треугольника, то они конгруэнтны.

Площадь треугольника

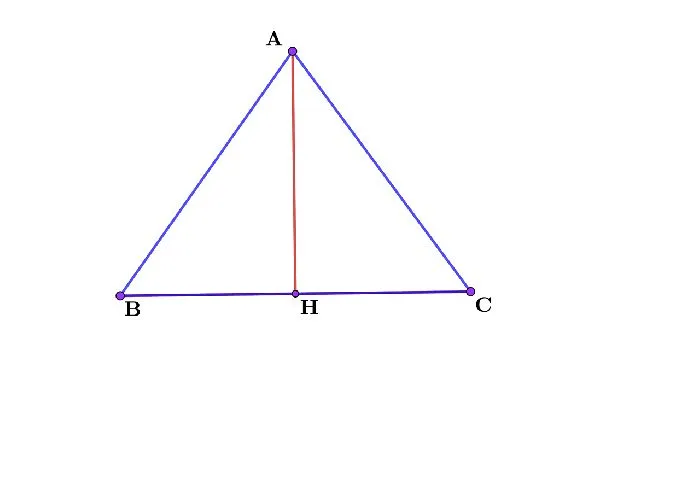
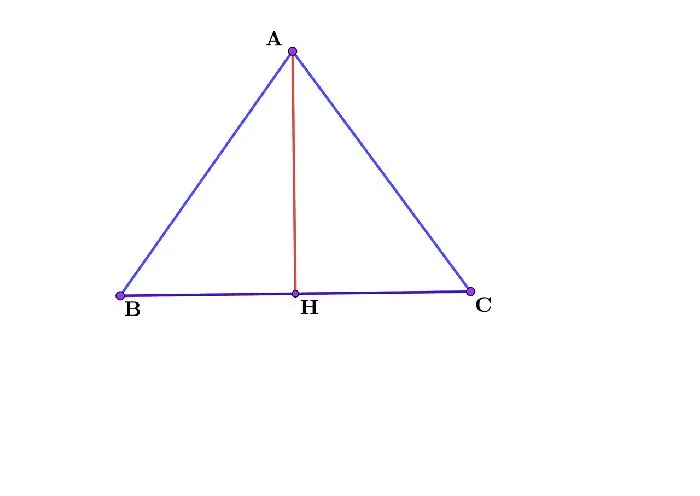
Площадь треугольника, если известны высота и основание, на котором он построен.

Площадь треугольника с двумя известными сторонами и углом между ними.

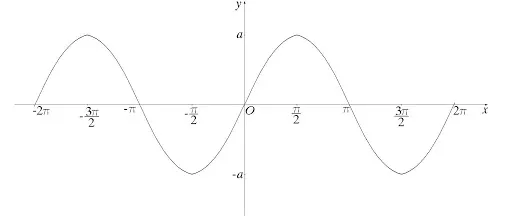
Площадь правильного треугольника с известными перпендикулярами

Площадь правильного треугольника, когда известна только сторона

С помощью формулы Герона можно вычислить площадь треугольника, если известны его стороны

Площадь треугольника, если известны радиус и радиус эндоцикла.

Площадь треугольника, если известны стороны и радиус контура

Прямая

В геометрии каждый объект состоит из основных элементов: Точки, линии и поверхности. Любая форма, будь она плоской или трехмерной, состоит из этих элементов. Определение точки понятно, но понять, что такое линия и как она может быть бесконечной, в пятом классе нелегко.

Определение прямой

Определение линии начинается с определения линии. Что такое линия? Это ряд точек, которые соединены между собой. Линия может быть прямой, изогнутой, пунктирной, непрерывной или даже открытой. И из-за этого разнообразия линии в пространстве очень трудно определить. Неясно, как будет работать та или иная кривая, когда она покинет лист. По этой причине был выделен один конкретный тип линий — прямые линии.

Когда в разговоре вы слышите о прямых линиях, люди имеют в виду прямые линии, но обычно последнее слово в предложении опускается.

Что такое прямая линия в математике? Прямые линии — это бесконечные, непрерывные линии, которые не имеют искривлений. Первое правило для линий гласит, что через любые две точки можно провести прямую. Однако не всегда можно провести прямую через три точки. В большинстве случаев через три точки можно провести три линии.

Если прямая проходит через три точки, то говорят, что эти точки лежат на прямой. Линии обычно обозначаются маленькой латинской буквой или названием двух точек на линии.

Почему два, а не три? Проще говоря, через две точки может проходить только одна прямая. Тогда как через одного: бесконечное число. И не имеет смысла использовать три точки: Нет смысла усложнять символику.

Взаимное расположение прямых

Две линии в пространстве могут быть расположены по-разному. Самый простой и распространенный случай — это перекресток. Когда две прямые имеют общую точку, эти прямые пересекаются.

Как можно назвать линии, если они не пересекаются? Тогда они параллельны, то есть не имеют общих точек.

А что происходит, когда две прямые имеют две или более общих точек? Тогда линии совпадают.

Пересечение двух прямых дает две пары вертикальных углов. Вертикальные углы в каждой паре равны.

Если угол пересечения равен 90 градусам, то линии перпендикулярны друг другу.

Если стороны одного угла являются дополнительными биссектрисами сторон другого угла, то такие углы называются прямыми. (Рисунок 6)

Теорема: Прямые углы равны.

Доказательство. Пусть a₁β₁и α₂β₂— быть заданы вертикальные углы. Угол α₁является касательной к углу b₁. Угол b₁примыкает к углу a .₂. Тогда:

Аналогично можно показать, что β.₁= β₂.

Рисунок 6 Вертикальные углы.

Перпендикулярные прямые

Если две линии пересекаются под прямым углом, эти линии называются перпендикулярами. (Рисунок 7)

Теорема: Через каждую точку на прямой, перпендикулярной данной прямой, может проходить только одна прямая.

Доказательство.

Пусть a — заданная прямая, а A — заданная точка, принадлежащая прямой a. Обозначим a через a, прямую a через полупрямую a1. Определите угол между полупрямой a1 и углом 90° — a1b1. Тогда прямые a и b, на которых прямые a1 и b1 перпендикулярны.

Предположим, что существует другая прямая, перпендикулярная a и проходящая через A, — прямая c. Определите угол 90° между полупрямыми a1 и a1c1. Докажите, что можно вычислить еще один угол в 90° от полупрямой, ведущей из начала координат (точка A) к этой полуплоскости. Однако это невозможно, поскольку, согласно аксиоме 7, из каждой полупрямой, идущей от начала координат к данной полуплоскости, можно определить только один угол данной меры. Поэтому в данной полуплоскости не может быть двух углов 90° к одной и той же полуплоскости. Теорема доказана.

Рис.7 Вертикальные линии.

Признаки равенства треугольников

Первое доказательство равенства треугольников

Теорема: Если две стороны и угол между этими сторонами треугольника равны двум сторонам и углу между этими сторонами другого треугольника, то эти треугольники равны. (Рисунок 8).

Доказательство.

Даны два треугольника ABC и A 1 B 1 C 1. Угол A = A 1, стороны AB = A 1 B 1 AC = A 1 C 1 (рис. 8a).

Возьмем третий треугольник A 1 B 2 C 2 = ABC. Возьмем треугольники A 1 B 1 C 1 и A 1 B 2 C 2 так, чтобы стороны A 1 B 1 и A 1 B 2 лежали на полупрямой, а A1 — начальная точка нашей полупрямой. Вершина B 2 лежит на полулинии A 1 B 1, а вершина C 2 лежит на той же полуплоскости, что и C 1 (рисунок 8b). (Рисунок 8b). Согласно аксиоме 6: В каждой полулинии из начальной точки можно провести только один отрезок определенной длины. Следовательно, сторона A 1 B 2 = A 1 B 1, то есть точки B 1 и B 2 совпадают.

Согласно аксиоме 7: Из любой полупрямой, проведенной из начальной точки в определенную полуплоскость, можно построить только угол определенной меры. Поэтому углы C 1 A 1 B 1 и C 2 A 1 B 2 равны, то есть точки C1 и C2 совпадают. Поэтому треугольники A 1 B 1 C 1 и A 1 B 2 C 2 совпадают. Поэтому треугольники ABC и A 1 B 1 C 1 также равны.

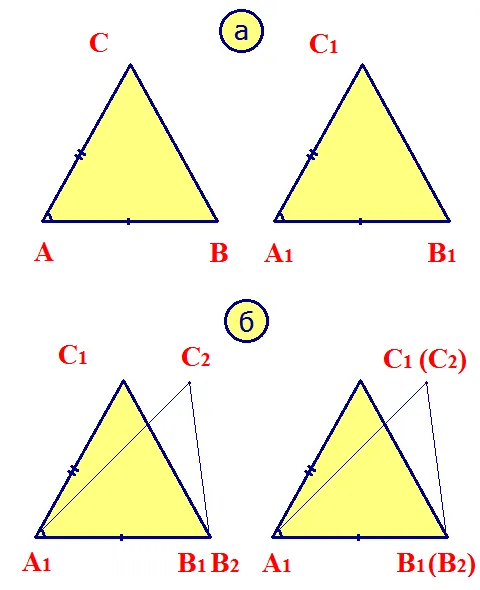
Рис.8 Первое доказательство равенства треугольников.

Второе доказательство равенства треугольников

Теорема: Если сторона и прилежащие углы треугольника равны стороне и прилежащим углам другого треугольника, то эти треугольники равны. (Рисунок 9).

Доказательство.

Даны два треугольника ABC и A 1 B 1 C 1. Угол A = A 1, B = B 1 Сторона AB = A 1 B 1 (рис. 9).

Возьмем третий треугольник A 1 B 2 C 2 = ABC. Треугольники A 1 B 1 C 1 и A 1 B 2 C 2 таковы, что стороны A 1 B 1 и A 1 B 2 лежат на полупрямой, а точка A1 является началом нашей полупрямой. Вершина B 2 лежит на полулинии A 1 B 1, а вершина C 2 лежит на той же полуплоскости, что и C 1 (рисунок 9). Так как по условию AB = AB = A 1 B 1 и AB = A 1 B 2, то A 1 B 1 = A 1 B 2, то есть точки B 1 и B 2 совпадают.

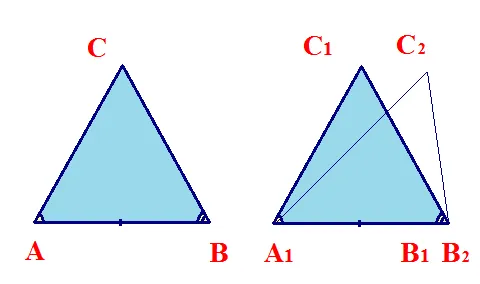
Рис. 9 Вторая точка равенства треугольников.

Поскольку угол B 1 A 1 C 2 равен углу B 1 A 1 C 1, а угол A 1 B 1 C 2 равен углу A 1 B 1 C 1, сторона A 1 C 2 совпадает со стороной A 1 C 1. А сторона B 1 C 2 равна стороне B 1 C 1. То есть, вершины C 1 и C 2 совпадают. Поэтому треугольник A 1 B 1 C 1 конгруэнтен треугольнику A 1 B 2 C 2 и, следовательно, соответствует треугольнику ABC.

Третья точка равенства треугольников

Теорема: Если три стороны треугольника равны трем сторонам другого треугольника, то эти треугольники равны. (Рисунок 10).

Доказательство.

Два треугольника ABC и A 1 B 1 C 1 имеют стороны AB = A 1 B 1, BC = B 1 C 1, AC = A 1 C 1 (рисунок 10).

Возьмите третий треугольник A 1 B 1 C 2 = ABC и расположите треугольники A 1 B 1 C 1 и A 1 B 1 C 2 так, чтобы вершина C 2 лежала в той же полуплоскости, что и вершина C 1 (рисунок 10). Пусть D — середина отрезка C 1 C 2. Поэтому треугольники C 1 A 1 C 2 и C 1 B 1 C 2 равнобедренные. A 1 D и B 1 D — медианы, то есть высоты этих треугольников. Но через точку D может пройти только прямая, перпендикулярная прямой C 1 C 2. Таким образом, возникает противоречие. Треугольники ABC и A 1 B 1 C 1 равны.

Взаимное расположение прямых

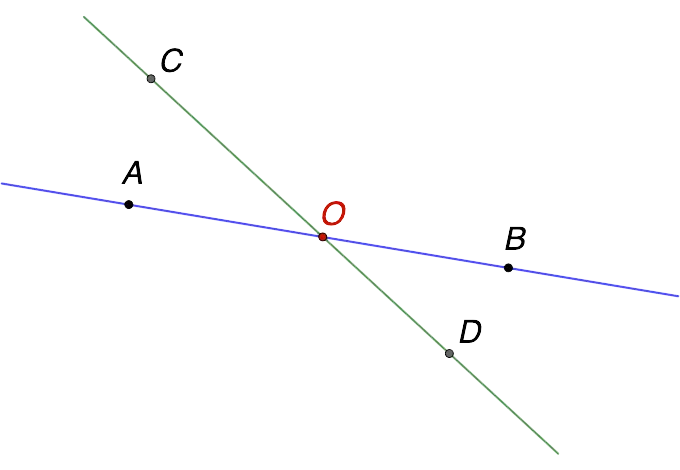
Если мы рассматриваем две прямые на плоскости, то они могут по-разному располагаться по отношению друг к другу:

1. Параллельные прямые – не пересекаются, следовательно, у них нет общих точек. Параллельность в геометрии обозначается двумя вертикальными черточками. В нашем случае записывается так:
2. Пересекающиеся прямые – как следует из названия, линии пересекаются и имеют одну общую точку (на рисунке ниже – это точка O).
3. Перпендикулярные прямые – пересекаются под прямым углом (90 градусов). Перпендикулярность линий обозначается специальными символом – ⊥. То есть пишем таким образом:

Примечание: В трехмерном пространстве линии могут пересекаться, то есть лежать в разных плоскостях.

Геометрия 7 класс. Точка, прямая и отрезок

Кажется, что такие простые термины, как «точка» или «линия», которые мы используем каждый день в нашей жизни, очень легко определить. На практике, однако, было показано, что это не так.

Существует множество определений терминов «точка» и «линия», данных известными математиками. На протяжении веков ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Давайте придерживаться тех объяснений, которые, на наш взгляд, описывают их наиболее просто.

Точка — это элементарная фигура, не имеющая частей.

Линия состоит из множества точек и простирается бесконечно в обоих направлениях.

На рисунке изображена прямая a и точки D, F, G и H. Точки F и G лежат на прямой a. Точки D и H не лежат на прямой a.

В тексте точка отмечена знаком «(-)».. Включение и невключение точки в прямую обозначается символами «∈» и «∉». Вспомогательный символ может быть сохранен как зеркальное изображение буквы «E» или как символ евро «€».

То есть, в геометрических терминах, информация о положении линии и точек на приведенном выше рисунке может быть записана следующим образом:

• (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a );
• (·)G ∈ a — точка G принадлежит прямой a ;
• (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a );
• (·)H ∉ a — точка H не принадлежит прямой a .

Как обозначить прямую

Прямая линия обычно обозначается маленькой латинской буквой.

Линия, на которой отмечены две точки, иногда обозначается большими латинскими точками, соответствующими названиям этих точек.

На рисунке изображены:
• Прямая a
• Прямая f
• Прямая CH
• Прямая DK

Точки D, E и F лежат на одной прямой, поэтому прямая DE, прямая EF и прямая DF — это три разных названия одной и той же прямой.

Задача № 1 из учебника Атанасян 7-9 класс

Постройте прямую, обозначьте ее буквой a и отметьте точки A и B на этой прямой, а также точки P, Q и R, которые не лежат на этой прямой. Опишите взаимное расположение точек A, B, P, Q, R и прямой a с помощью символов ∈ и ∉ .