Что такое алгоритм в математике. Что такое алгоритм в математике.

Первый коридор этого пути красный, потому что начинается от точки А, а последний — зеленый, потому что Тесей не дошел до него в своих поисках Минотавра. Скажите

Значение слова «алгоритм» очень похоже на значение слов «рецепт», «метод», «процедура». Но в отличие от рецепта или метода, любой алгоритм обязательно обладает следующими свойствами.

1. усмотрение. Выполнение алгоритма делится на последовательность полных шагов действий. Только после выполнения одного действия можно переходить к выполнению следующего. Выполнить каждое действие исполнителю предписывает специальная команда в файле алгоритма, называемая инструкцией.

2. детерминизм. Каждая инструкция алгоритма определяет уникальное действие исполнителя и четко указывает, какая инструкция должна быть выполнена следующей. Когда алгоритм многократно применяется к одному и тому же набору входных данных, каждый раз получаются одни и те же промежуточные и выходные результаты.

3. чистота. Алгоритм не должен содержать инструкций, смысл которых может быть неоднозначно понят исполнителем, т.е. алгоритм должен быть достаточно ясным и полным, чтобы исполнителю не приходилось принимать самостоятельных решений. Следует помнить, что алгоритм всегда должен выполняться «не думающим» исполнителем.

4. эффективность. Это свойство относится к существенной уверенности в результате отдельных шагов и алгоритма в целом. При точном выполнении инструкций алгоритма процесс должен быть завершен за конечное число шагов и одновременно должен быть получен ответ на проблему. Одним из возможных ответов может быть тот факт, что решения проблемы не существует. Свойство эффективности включает в себя свойство конечности — завершение алгоритма за конечное число шагов.

5. массивность. Алгоритм подходит для решения любой задачи из определенного класса задач, т.е. алгоритм работает правильно при определенном наборе входных данных, называемом областью применения алгоритма.

Докажите, что метод Эратосфена, рассмотренный в примере 2, является алгоритмом.

Не каждый пошаговый метод решения проблемы является алгоритмом. Давайте проверим это на примере.

Пример 3. Опишем способ построения перпендикуляра к прямой MN, проходящего через заданную точку A на этой прямой, с помощью линейки и компаса (рис. 2.2):

1) с помощью компаса начертите отрезки одинаковой длины с концами B и C по обе стороны от точки A на прямой MN; 2) увеличьте раствор компаса до радиуса, в полтора-два раза превышающего длину отрезков AB и AG; 3) с помощью изображенного кругового решения проведите дуги окружности с центрами B и C так, чтобы они охватывали точку A и образовывали два пересечения между ними (B и E); 4) возьмите прямую линию, закрепите ее в точках B и B и соедините с отрезком; если этот отрезок построен правильно, то он пройдет через точку A и будет перпендикулярен прямой MN.

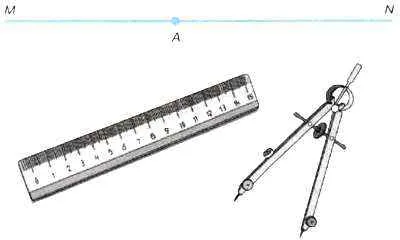
Рисунок 2.2: Проведение линии, перпендикулярной прямой линии

Почему этот метод построения перпендикуляра к прямой не является алгоритмом? Какое свойство алгоритмов здесь нарушено?

Бывают проблемы, которые человек решает успешно, но не может представить процесс решения в виде последовательности шагов.

Например, если предъявить человеку картинки с изображением собак и кошек и попросить его распознать, на каких картинках изображены собаки, а на каких кошки, он решит эту задачу почти сразу и правильно. Пока не удалось написать формальный алгоритм для решения этой и подобных проблем, хотя в этой области, известной как теория распознавания образов, был достигнут определенный прогресс.

2. Способы записи алгоритма

Из базового курса информатики в школе вы знаете различные способы записи одного и того же алгоритма:

— словесная запись алгоритма на естественном языке; — запись алгоритма на псевдокоде; — частично стандартизированный естественный язык с элементами языка программирования и общепринятой математической нотации; — запись алгоритма в виде блок-схемы; — детальное графическое представление логической структуры программы или алгоритма с использованием стандартизированных блоков, соединенных линиями (символами понятий); — запись алгоритма на языке программирования и т.д.

Решение о том, как записать алгоритм, зависит от нескольких причин. Небольшой алгоритм также может быть записан в словесной форме. Если для вас важна ясность, имеет смысл использовать блок-схему. Алгоритм, который должен быть реализован, должен быть написан на языке, понятном исполнителю.

Правила выполнения блок-схем, внешний вид графических блоков и их именование определены в ГОСТ 19.701-90 (ISO 5807-85) «Схемы алгоритмов, программ, данных и систем. Символы и правила исполнения».

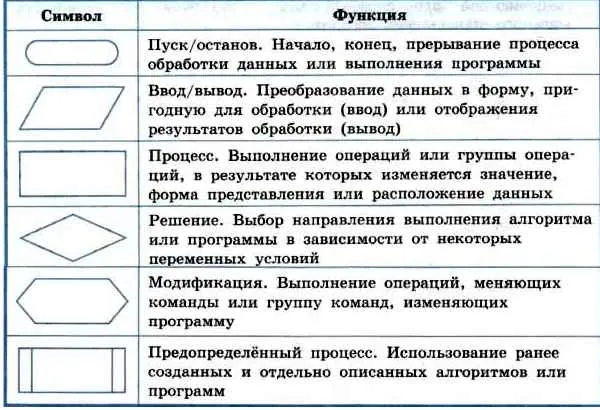
Давайте вспомним основные графические символы, которые мы будем использовать в дальнейшем (табл. 2.1).

Таблица 2.1.

Основные символы блок-схем и функции, которые они представляют.

Пример 4: Вспомните детскую игру «угадайка». Первый игрок загадывает целое число и говорит второму игроку, из какой области оно взято. Второй игрок должен угадать число как можно быстрее. Второй игрок может назвать число, а первый игрок должен сказать, меньше или больше угаданного им числа. Игра заканчивается, когда называется число, соответствующее угаданному.

Предположим, что угадано число X ? A, B. Представим алгоритм решения этой задачи в виде блок-схемы — метода половинного деления, с которым вы знакомы (рис. 2.3).

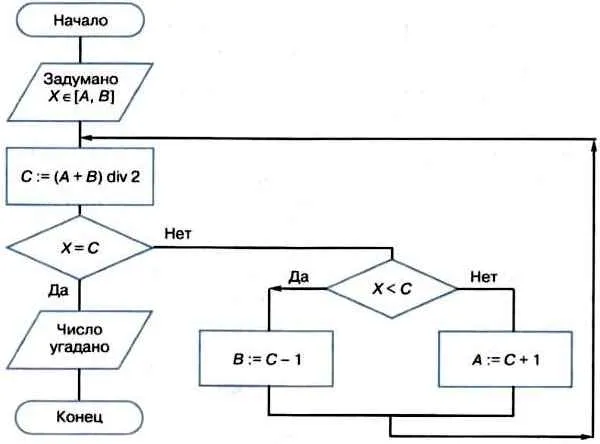
Рисунок 2.3: Метод половинного деления

Вычислите максимальное количество шагов, необходимое для угадывания числа X с помощью этого метода? 0, 100.

3. Понятие сложности алгоритма

В теории алгоритмов говорят, что для задачи, для которой существует алгоритмическое решение, возможно множество различных путей решения, т.е. алгоритмов.

Так какой же алгоритм лучше всего подходит для решения конкретной задачи? По каким критериям его следует выбирать из множества возможностей?

Алгоритм можно назвать сложным и запутанным, поскольку он имеет разветвленную логическую структуру с множеством проверок условий и переходов. Однако компьютер может легко выполнить программу, реализующую такой алгоритм, поскольку он выполняет одну инструкцию за другой, и не имеет значения, является ли это операцией умножения или проверкой условия.

Теория алгоритмов предоставляет инструменты для анализа различных алгоритмов решения одной и той же задачи, на основе которых можно выбрать наиболее эффективный (лучший) алгоритм.

Вычислительный процесс, создаваемый алгоритмом, — это последовательность шагов, которые алгоритм проходит в процессе выполнения.

Сложность алгоритма — это количество элементарных шагов (действий) в вычислительном процессе алгоритма.

Обратите внимание, что определение сложности алгоритма относится к вычислительному процессу, а не к самому алгоритму.

Алгоритм состоит из инструкций.

Инструкция — это одна команда в описании алгоритма. Шаг в алгоритме — это одно действие, которое исполнитель выполняет над инструкцией. В циклических алгоритмах количество шагов в выполнении алгоритма может быть намного больше, чем количество инструкций в алгоритме из-за повторения одних и тех же инструкций.

Конечно, количество операций при выполнении алгоритма во многом зависит от объема обрабатываемых данных. На самом деле, сортировка списка из 100 фамилий в алфавитном порядке требует значительно меньше операций, чем сортировка списка из 100 000 фамилий. Поэтому сложность алгоритма выражается как функция от количества входных данных.

Например, алгоритм, который только считывает данные и хранит их в оперативной памяти, имеет линейную сложность O(n) (считывает «o big from en»). Существуют алгоритмы с квадратичной и кубической сложностью.

Для решения этой задачи могут быть разработаны алгоритмы различной сложности. Алгоритм с наименьшей сложностью считается лучшим среди них.

Помимо сложности, важным свойством алгоритма является эффективность. Эффективность оценивается по количеству элементарных операций, необходимых для решения задачи, и памяти, необходимой для работы алгоритма.

Пример 5: Известно, что многие языки программирования не знают экспоненции, поэтому программисту приходится самому писать такой алгоритм. Операция умножения выполняется с помощью операций умножения. С увеличением коэффициента возрастает и количество операций умножения, на выполнение которых уходит много времени. Поэтому вопрос разработки эффективного алгоритма для экспоненты является важным.

Рассмотрим метод быстрого вычисления натуральной силы n действительного числа x, который был описан еще в Древней Индии, то есть до нашей эры.

1. запишите p в двоичной системе счисления. 2. в этой нотации замените каждую единицу парой букв KX, а каждый ноль — буквой K. 3. удалите самую левую пару KX. 4. полученная строка, прочитанная слева направо, дает правило для быстрого вычисления x n, если рассматривать букву K как операцию возведения в квадрат, а букву X — как операцию умножения результата на x. В начале результат равен x.

Алгоритмы

Чтобы успешно применять современный анализ данных, нам необходимо познакомиться с понятием алгоритма. Алгоритм — это фундаментальное понятие в математике и современном анализе данных.

Алгоритм — это серия последовательных действий, направленных на достижение определенной цели.

Алгоритмы используются не только в математике, но и во всех областях человеческой деятельности. Даже часть творческой работы, например, создание скульптуры или картины, может быть алгоритмизирована, как это видно в классических академических работах.

Лучший способ познакомиться с понятием алгоритма — использовать примеры.

Мы начнем с классического примера — алгоритма Евклида.

Алгоритм Евклида

Предположим, у вас есть два натуральных числа a и b, например, 2014 и 15. Ваша цель — найти наибольший общий делитель этих чисел.

Поэтому нужно найти делитель, который, во-первых, должен быть общим для двух чисел и, во-вторых, максимальным.

Очевидно, что существует столько же различных задач такого рода, сколько существует различных пар чисел a, b.

Нужно найти последовательность, которая подходит для всех натуральных чисел a и b.

Давайте попробуем разобраться в проблеме и понять, как Евклид придумал этот алгоритм.

Очевидно, вначале он обозрел два числа и предположил, что одно из них больше другого, например, a>b .

Тогда можно предположить, что b является таким делителем.

Вопрос: Как я могу это проверить?

Деление является обобщением вычитания, поэтому мы последовательно вычитаем число b из числа a. Мы делаем это несколько раз подряд, пока не достигнем значения 0.

Если мы получим 0, то решение найдено, b — наибольший делитель, который мы ищем.

Но мы не находим 0, и на определенном шаге имеем остаток — b1 меньше b, и мы не знаем, что делать дальше.

Имеет смысл сосредоточиться на этом остатке.

Мы предполагаем, что если существует общий делитель, то он должен лежать в этом остатке b1 .

Задача. Попробуйте доказать, что это действительно так!

Поэтому мы можем продолжить остаток b1, вычесть его из a и повторить этот процесс несколько раз.

Наконец, мы приходим к выводу: либо общего делителя не существует, либо мы находим максимальный делитель двух чисел, в этом случае процесс останавливается на конечном числе шагов.

Мы применили эти действия к двум числам, предполагая, что a>b .

Если это неравенство не выполняется, мы просто меняем местами числа и достигаем цели.

Конечно, это не единственный способ найти максимальный делитель. Мы могли бы предложить простую процедуру перебора, в которой мы меняем местами числа от 1 до b по одному и проверяем, делят ли они полностью исходные числа или нет.

Конечно, алгоритмы можно сравнивать по количеству операций или количеству усилий, которые вы прикладываете для достижения цели, а также по количеству используемых ресурсов.

Анализ данных означает разложение сложного на простые элементы. Натуральное число состоит из единиц, которые делятся на единицы, а затем снова собираются вместе. Также можно разделить число на факторы или другие элементы.

Алгоритмы, которые сводят решение к четырем числовым шагам, называются арифметическими алгоритмами.

Они играют важную роль во многих различных областях математики.

Например, предположим, что нам нужно решить систему из двух уравнений первого порядка с двумя неизвестными:

Алгоритм решения этой системы вытекает из следующих формул

в котором полностью выражены как состав операций, так и порядок их выполнения.

Эти формулы обеспечивают одну и ту же цепочку операций для всех задач такого типа (т.е. для любых коэффициентов).

Конечно, мы должны предположить, что знаменатели не становятся равными 0.

Можно написать последовательность действий, которая учитывает все вариации значений коэффициентов уравнений. Также можно шаг за шагом устранять одно неизвестное и определять значение остальных неизвестных, как это делается в школе. Важен сам принцип работы алгоритма.

Примеры

Вот пример класса задач того же типа, для которых у современной математики нет алгоритма.

Рассмотрим все возможные дифференциальные уравнения, т.е. уравнения вида

где P — многочлен с целыми коэффициентами.

Уравнения названы в честь древнегреческого математика Диофанта. Диофант Александрийский был древнегреческим математиком, жившим, вероятно, в третьем веке нашей эры.

Самым важным трудом Диофанта является «Арифметика в 13 книгах», из которой сохранились только первые 6 из 13 книг.

Примеры диофантовых уравнений:

Из которых первое содержит два неизвестных, а второе — одно неизвестное (в общем случае рассматриваются уравнения с любым числом неизвестных).

Уравнение может иметь или не иметь интегральное решение.

Первое из приведенных выше уравнений имеет интегральное решение.

Второе уравнение не имеет интегрального решения, так как для любого целого числа x выполняется неравенство

В 1901 году немецкий математик Давид Гильберт огласил список из 20 трудных задач, среди которых была следующая задача:

Это требует разработки алгоритма, позволяющего выяснить для каждого диофантова уравнения, имеет ли оно интегральное решение.

Позже многие математики решили эту проблему Гильберта; окончательное доказательство было получено советским математиком Ю.В. Матиясевичем (см. Ю.В. Матиясевич Диофантова природа перечислимых множеств // Доклады Академии наук СССР. — 1970. — Т. 191. — № 2. — С. 279-282).

Ю.В. Матиясевич, Десятая проблема Гильберта — М.: Наука: Физико-математическая литература, 1993 г. — 223 с. — (Математическая логика и основания математики; выпуск № 26) -ISBN 502014326X.

Такой алгоритм известен для частного случая уравнения Диофанта с одним неизвестным.

с целочисленными коэффициентами.

Если уравнение имеет целочисленный корень, то он обязательно делится на .

Алгоритм нахождения такого корня прост: необходимо перечислить все делители свободного члена:

1. найти все делители числа (их конечное число);
2. подставлять поочередно найденные делители в левую часть уравнения и вычислять численное значение ее;
3. если при подстановке некоторого делителя левая часть уравнения приняла значение 0, то данный делитель является корнем уравнения
4. если ни для какого делителя левая часть уравнения не обращается в 0, то уравнение не имеет целочисленных корней.

Отметим общие свойства алгоритмов.

Необходимо, чтобы метод расчета мог быть передан другому лицу в виде конечного числа инструкций, поскольку он должен перейти к отдельным этапам расчета.

При этом расчеты по данным инструкциям не зависят от произвола исполнителя и представляют собой определенную процедуру, которая может быть повторена и выполнена в любое время другим лицом.

Алгоритм решает не одну задачу, а серию задач одного типа.

Ниже мы используем выдержки из увлекательной книги «Алгоритмы и решение машинных задач» Б.А. Трахтенброта и обсудим некоторые интересные алгоритмы.

Задача Тезея и алгоритм поиска чудовища

Греческая мифология рассказывает о легендарном герое Тесее, который вошел в лабиринт, чтобы найти чудовищного Минотавра. Ариадна помогла ему выйти из лабиринта, дав Тесею клубок ниток, один конец которого она сама держала в руке. По мере того как Тесей углублялся в лабиринт, клубок разматывался; размотав нить, Тесей благополучно возвращался к выходу.

Алгоритм сложения

В предыдущей статье этой серии с загадочным числом 101 мы уже рассмотрели «маленький» пример приготовления торта и узнали о трех способах создания алгоритмов: случайное обнаружение алгоритмов, объединение алгоритмов и эволюционное накопление алгоритмов. Эти методы хороши — с их помощью алгоритмы успешно, но очень медленно развивались и будут развиваться дальше. Но так получилось, что они стали основой для следующих двух. Эти методы: алгоритмический перевод и перевод алгоритма с модели. И благодаря этому соединению, как это было с Алисой и встречей Тралала, все начало развиваться гораздо более увлекательным образом и, что более важно, позволило гораздо быстрее создавать новые и более сложные алгоритмы. Так что же такое близнецы трансфер и перевод? И почему необходимо различать их, чтобы продолжать говорить об алгоритме?

Данная статья посвящена ответам на эти вопросы. И чтобы начать наше приключение, нам нужно использовать результат предыдущей статьи. Вы должны попробовать волшебный торт с надписью «Съешь меня». Не пробуйте его ради того, чтобы попробовать, а используйте его как рабочий метод для анализа формирования сложного алгоритма.

И эта статья будет особым алгоритмом. Для наших целей очень подходит простой «алгоритм сложения», который мы уже знаем. Мы познакомились с ним в первой статье этой серии.

Давайте немного развлечемся, оценивая структуру этого «математического действия», которое является элементарным для многих наших проблем. В конце концов, эта элементарность не сразу бросается в глаза. И для Алисы это действие все еще трудно и не всегда дается.

Что такое один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один плюс один?

— Я не знаю, — ответила Алиса, — я сбилась со счета.

Поможем Алисе научиться такому сложению? Представим себе ситуацию «старого математика», которому, возможно, впервые понадобилась эта математическая операция. Этому «математику» тоже было что считать. Конечно, это не слова «один» в формулировке королевы, но и они были очень близки к одним и тем же объектам. Ну, например, коровы в большом стаде. И даже если в его стаде изначально было три или семь коров, «математик», глядя на коров, всегда мог легко увидеть их «число». Изначально это «число» даже не было числом. Это был способ оценить количество соломинок, которыми нужно было обеспечить стадо на зиму. Или оценить, сколько времени необходимо для заготовки сена.

На примере стада коров попробуем понять последовательность событий и действий человека, ухаживающего за стадом, которая приводит к «алгоритму сложения». Мы зависим от определенных событий. Например, человек, ухаживающий за стадом (далее мы будем условно называть его «пастух»), знает, что корове нужно полдня, чтобы заготовить сено на зиму. Основываясь на этих знаниях, мы можем попытаться спланировать затраты труда «пастуха» (нам нужно написать алгоритм для расчета затрат труда). Для этого не требуется знание слова «количество», равно как и знание «чисел».

Этот алгоритм также основан на базовой стратегии «поддержания жизнеспособности», и чтобы сократить количество слов в этой статье, мы пропускаем несколько этапов эволюционного развития и переходим непосредственно к более примитивному алгоритму пастуха. Упростим ситуацию со стадом и оставим в нем только одну корову.

Перенос

Пока еще рановато использовать цифры, но мы уже близки к этому. Давайте выберем что-то более простое и чистое. Я бы посоветовал Алисе следить за своими пальцами. Ну, для пастуха пальцев недостаточно. Но вы всегда можете найти предмет меньше коровы, чтобы держать его в руке, например, гальку. И что вы с ними делаете? Подберите их правильно! Палец можно сравнить со словом «один». А камешек сопоставляется с коровой. Легко сказать «совпадает». И с помощью какого алгоритма вы можете это сделать?

У Алисы ситуация проще. Для каждого слова «один», которое она слышит, ей достаточно «завершить» один палец на руках. Для «пастуха» это противостояние немного сложнее, но принцип схож. Стадо также должно быть выстроено в структуру — желательно линейную, как слова «один» в предложении королевы. Это можно сделать, например, утром, когда коровы выходят из коровника через узкую дверь, через которую за один раз может пройти только одна корова. Необходимо заранее подготовить гальку. И за каждую корову, которая выходит, вы берете камешек и «сгибаете его», ну нет, не палец Алисы, конечно. Хранить его нужно в отдельном месте по вашему выбору. Это позволит создать каирн. И когда выходит последняя корова, в куче оказывается столько же камней, сколько коров в стаде. Так зачем же нам нужны эти кривые пальцы и груда камней? Точно! С ними легче работать, чем с длинным предложением, которое рассыпается в памяти, или с большим стадом. Вы можете рассчитывать с их помощью. Имея кучу камней, легко разработать алгоритм зимовки сена в хранилище, отдельном от коровника. И многое другое может быть сделано. Мы изменили алгоритм хранения сена с коров на камни. И мы упростили жизнь пастуха, сделав ее немного более математической.

Он был в одном шаге от того, чтобы стать серьезным математиком. Этот шаг — возникновение акта сложения. И этот шаг очень прост. Например, вам нужны два «пастуха», у каждого из которых в кармане есть куча камешков, принадлежащих их стаду. В этом случае достаточно иметь ситуацию, когда необходимо объединить две стаи. В этом случае, конечно, можно провести объединенное стадо через хлев с узкой дверью. Но гораздо проще бросить две кучи камешков в одно место!

Возможно, именно так и появился алгоритм сложения! Так родилась математика. Повышение эффективности алгоритмов путем их перемещения в более удобное место. Сначала это были просто камешки, позже добавились числа, интегралы, исчисление предикатов и многое, многое другое.

Но как насчет другого близнеца, «перевода»? Да, да… нам это нужно, и Алисе это нужно.

Трансляция

— ‘Прибавление не знает’, — сказала Черная Королева.

— ‘Вы умеете вычитать? Вычтите девять из восьми.

— Я не знаю, но…

Но…? Что так смущало Алису? Ответ прост, а разгадка будет в том, что этот момент не только смутил Алису, он остро мучил и «старого математика». Сложность момента сводится к простому осознанию: не все математические операции с «камнями» однозначно соответствуют (т.е. не переносятся) на стадо коров. А отрицательные числа — это, пожалуй, самая простая и первая проблема, с которой когда-либо сталкивалась математика. Очень непонятно, какая корова соответствует отрицательному числ у-1.

И тут возникает вопрос. Отвергаем ли мы эти «странные» отрицательные числа? Или их можно использовать, но не применять к коровам? С теми знаниями, которые доступны современному школьнику, ответ тривиален. Конечно же, используйте их! И очевидно, что Алисе в какой-то момент придется выучить такое «странное» вычитание. Но для «старых математиков» все было не так просто. И только полезность алгоритмов с отрицательными числами помогла им принять это непростое решение и утвердительно ответить на поставленный вопрос. Да, отрицательные числа следует использовать!

Такие же любопытные вопросы, как и вопрос об «отрицательных числах», впоследствии не раз занимали математиков. Вопросы были запутанными, как и у гусеницы, и каждый раз новое вычитание становилось все «страннее» и «страннее». Логические числа вместо рациональных (например, алгоритм определения длины окружности по ее диаметру). Квадратный корень из отрицательного числа («мнимое число»), например, для алгоритма решения кубического уравнения. «Бесконечность», например, найти предел сходящейся суммы бесконечного ряда (уже греческий философ Зенон задумался над этой странной проблемой в своем парадоксе «Ахиллес и черепаха»). До появления математиков существовало множество парадоксов. Некоторые даже были исключены, потому что не было возможности использовать их в полезных алгоритмах. Так было, например, с парадоксом «множества всех множеств». Однако в основе всех этих рассуждений и решений лежало одно — наличие полезных алгоритмов, в которых эти «странности» использовались. И здесь сработал «естественный отбор». И эволюционный путь формирования математических алгоритмов, с медленным и дополнительно быстрым накоплением, привел к тому, что мы сегодня называем «математикой».

И где разница между близнецами «перевод» и «трансфер». Вы с Алисой уже догадались. Определение перевода обязательно вводит ограничения и выделяет подмножество взаимно бесспорно соответствующих объектов и алгоритмов, в рамках которых может быть корректно осуществлен перевод между двумя алгоритмическими областями: областью приложения («стадо коров») и областью модели («горсть камешков»). За пределами этого подмножества передача невозможна. Так же, как невозможно «минус одна корова». Эти ограничения необходимы в представленной модели «отрицательных чисел». Самая простая модель, которую я смог найти. Но те же ограничения распространяются и на модели с гораздо более сложными переводами. Но давайте остановимся на этом. Давайте не будем объединять их всех вместе — в конце концов, мы имеем дело с чем-то более сложным, чем стадо коров.

Свойства алгоритмов

Дискретность. Алгоритм не является единой неделимой структурой, а состоит из отдельных небольших шагов или действий. Эти действия происходят в определенном порядке, и каждое из них начинается после завершения других.

Эффективность. Выполнение алгоритма должно привести к определенному результату и не должно оставлять неопределенности. Результат может быть и неудачным — например, алгоритм может сообщить, что решения нет, но оно должно быть.

Детерминизм. Ни на одном этапе не должно быть двусмысленности или непоследовательности; инструкции должны быть четко определены.

Массивность. Алгоритм обычно можно распространить на аналогичные задачи с другими начальными данными — при условии, что вы измените начальные условия. Например, типичный алгоритм решения квадратного уравнения остается неизменным независимо от чисел, используемых в уравнении.

Ясность. Алгоритм должен содержать только те действия, которые известны и понятны исполняющему его человеку.

Совершенство. Алгоритмы конечны; они должны завершиться за определенное количество шагов и выдать результат, соответствующий определенным определениям.

Какими бывают алгоритмы

Несмотря на слово «последовательность», алгоритм не всегда описывает действия в строго определенном порядке. Это особенно актуально в современном мире, где асинхронность в программировании возрастает. В алгоритмах есть место для условий, циклов и других нелинейных конструкций.

Линейный. Это самый простой тип алгоритма: действия следуют одно за другим, каждое начинается после завершения предыдущего. Они не упорядочиваются, не повторяются и не выполняются ни при каких условиях.

Разветвление. Этот тип алгоритма имеет эффект ветвления: определенные действия выполняются только при выполнении определенных условий. Например, если число меньше нуля, оно должно быть удалено из структуры данных. Можно добавить вторую ветвь: что произойдет, если условие ложно — например, если число больше или равно нулю. Может быть более одного состояния, которые также могут сочетаться.

Циркуляр. Такие алгоритмы выполняются в цикле. Когда блок действий заканчивается, эти действия начинаются снова и повторяются определенное количество раз. Цикл может состоять из одного действия или последовательности, а количество итераций может быть фиксированным или зависеть от условия: например, повторять этот блок кода до тех пор, пока в структуре данных не останется пустых ячеек. В некоторых случаях цикл может быть бесконечно длинным.

Рекурсивный. Рекурсия — это явление, когда алгоритм вызывает сам себя, но с другими входными данными. Это не цикл: данные разные, но выполняется много «экземпляров» программы, а не один. Известным примером рекурсивного алгоритма является вычисление чисел Фибоначчи.

Рекурсию можно использовать для элегантного решения некоторых задач, но с ней нужно быть осторожным: такие алгоритмы могут сильно нагружать системные ресурсы и работать медленнее других.

Вероятностный. Такие алгоритмы упоминаются реже, но они очень интересны: работа алгоритма зависит не только от входных данных, но и от случайных величин. К ним относятся, например, хорошо известные алгоритмы Лас-Вегаса и Монте-Карло.

Основные и вспомогательные. Это еще один вид классификации. Основной алгоритм решает непосредственную задачу, вспомогательный алгоритм решает подзадачу и может быть использован в рамках основного алгоритма — для этого в нем просто указывается его имя и входные данные. Примером вспомогательного алгоритма является любая программная функция.

Графическое изображение алгоритмов

Алгоритмы могут быть записаны в виде текста, кода, псевдокода или графически — в виде блок-схем. Это специальные диаграммы, состоящие из геометрических фигур, которые описывают определенные действия. Например, начальная и конечная точка на диаграмме представляет начало и конец алгоритма, параллелограмм представляет входные или выходные данные, а ромб — условие. Простые действия изображаются прямоугольниками, а связанные фигуры — стрелками — они указывают на последовательности и циклы.

На диаграммах показаны конкретные действия, условия, количество итераций цикла и другие детали. Это позволяет лучше понять алгоритмы.

Алгоритм

Понятие алгоритма, фундаментальное понятие в математике и информатике, возникло задолго до появления компьютеров. Первоначально под словом алгоритм понимался способ выполнения арифметических операций с десятичными числами. Позже этот термин стал использоваться для обозначения любой последовательности действий, которые приводят к решению конкретной задачи. Само слово алгоритм появилось в Средние века, когда европейцы познакомились с процедурами выполнения арифметических операций, описанных узбекским математиком Мухаммедом бен Мусой аль-Хорезми. Слово алгоритм — это европеизированное произношение слов аль-Хорезми.

В современном значении слово алгоритм часто ассоциируется с алгоритмом Евклида, который предполагает нахождение наибольшего общего делителя (НОД) двух чисел.

Вот современное описание евклидова алгоритма с помощью блок-схемы (см. «Условные обозначения алгоритмов»):

Стрелка присваивания» (см. «Операторы в языке программирования»). В книге Евклида «Принципы» этот алгоритм, конечно, сформулирован не так (и сформулирован по-другому). В данном случае мы представили современную формулировку этого алгоритма и одну из распространенных визуальных форм алгоритмов протоколирования.

Каждый алгоритм не существует сам по себе, а предназначен для определенного исполнителя (см. «Исполнители алгоритмов»). Алгоритм описывается в инструкциях исполнителя, который будет выполнять алгоритм. Объекты, над которыми может действовать исполнитель, образуют так называемую среду исполнителя, а набор инструкций, которые исполнитель может выполнять, образует систему команд исполнителя (ECS).

Таким образом, алгоритм можно рассматривать как последовательность инструкций, которые управляют работой исполнителя (и предписывают ему выполнить последовательность действий).

Свойства алгоритма.

Значение слова алгоритм очень похоже на значение слов рецепт, инструкция. Однако алгоритм, в отличие от рецепта или метода, обязательно обладает следующими свойствами.

1. выполнение алгоритма делится на последовательность полных шагов действий. Только после завершения одного действия (инструкции) можно приступать к выполнению следующего. Это свойство алгоритма называется дискретностью. Для выполнения каждого действия исполнителю дается специальная команда в файле алгоритма (инструкция).

2. понятность — алгоритм не должен содержать инструкций, смысл которых может быть неоднозначно понят исполнителем, т.е. протокол алгоритма должен быть настолько ясным и полным, чтобы исполнителю не приходилось принимать самостоятельных решений. Алгоритм всегда предназначен для выполнения «недумающим» исполнителем. Алгоритм состоит из инструкций, содержащихся в CIP.

Рассмотрим известный пример «домашнего» алгоритма — алгоритм перехода дороги: «Посмотри налево. Если нет машин, идите по середине дороги. Если они есть, подождите, пока они пройдут, и т.д.». Представьте себе ситуацию: Слева стоит автомобиль, но он не движется — у него заменено колесо. Если вы считаете, что исполнитель алгоритма должен ждать, значит, вы поняли этот алгоритм. Если, с другой стороны, вы решаете, что можете перейти дорогу, потому что считаете, что алгоритм был изменен в связи с непредвиденными (по вашему мнению!) обстоятельствами, значит, вы не поняли смысла алгоритма.

В каких сферах их применяют

Алгоритмы буквально пронизывают всю вселенную. Сам термин «алгоритм», вероятно, происходит от имени средневекового арабского математика Аль-Хорезми.

В современной истории эта концепция стала известна широкой публике в середине XX века, когда в моду вошла кибернетика. Основные принципы компьютерных алгоритмов были разработаны в 1950-х и 1960-х годах, в том числе советскими учеными.

В каких сферах деятельности используются алгоритмы? Проще назвать области, в которых они не используются. На практике они массово используются в промышленном производстве и в сфере услуг, что привело к большому скачку благосостояния человеческого общества.

• На заводах и фабриках алгоритмам починены все рабочие процессы, во время которых изготавливаются товары народного потребления в количестве, достаточном, чтобы обеспечить всех. Наибольший прорыв в промышленности произошел, когда в производство начали внедряться станки с числовым программным управлением, изготавливающим детали по заранее подготовленным и закодированным в компьютерных решениях.
• Школьная программа – это алгоритм массового донесения знаний до миллионов детей и подростков.
• Специальный алгоритм боевой подготовки превращает молодых людей в защитников Родины.

Возьмите лист бумаги и запишите один за другим все действия, которые вы совершаете каждый день. Составьте список этих занятий на всю неделю. Скорее всего, вы обнаружите, что с понедельника по пятницу у вас достаточно круговой алгоритм, а в субботу происходит небольшое раздвоение.

В течение дня вы выполняете ряд линейных алгоритмов, которые приводят к определенному результату (приготовление и прием пищи, стирка одежды, выполнение профессиональных задач в офисе или магазине).

Кстати, автоматическая стиральная машина работает с разными алгоритмами цикла в зависимости от типа белья.

По каким алгоритмам работает поиск от Google и Яндекс

Типичный пример — работа поисковых систем. Как Яндекс и Google могут так быстро находить ответы почти на все вопросы пользователей, возникающие на миллионах веб-страниц в Интернете?

Как известно от инсайдеров, поисковые системы используют около 1 500 алгоритмов, позволяющих пользователям быстро находить любую информацию в интернете.

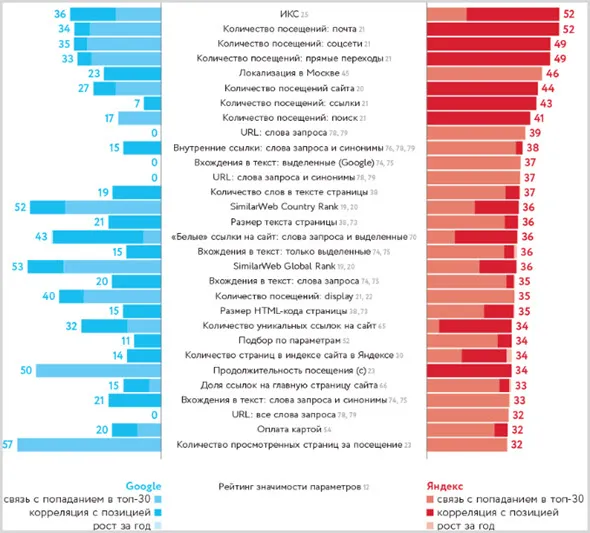
На самом общем уровне можно выделить три глобальных алгоритма поисковых систем.

• Индексация – сбор данных, опубликованных на всех сайтах в интернете.
• Определение релевантности. Информация на веб-страницах сортируется по тематикам поисковых запросов.
• Ранжирование. По каждой теме производится оценка качества и полезности ответов. Затем на странице результатов поиска ответы размещаются «по ранжиру», в порядке убывания качества и соответствия.

Многие пользователи полагают, что Google, начав поиск по определенному термину, обыскивает весь Интернет в поисках релевантной (связанной) информации.

Нет, это не так. Все содержимое всех веб-страниц заранее собирается специальными программами (которые также имеют алгоритмы) — так называемыми поисковыми роботами.

Собранная информация хранится в индексе поисковой системы — базе данных. Слово index в переводе с английского означает «каталог». Как и в обычной библиотеке, все книги разделены по полкам, а в указателе есть карточки с краткими описаниями. Индекс Яндекса — это такой цифровой каталог всего интернет-контента.

Когда пользователь начинает поиск по определенному вопросу, в дело вступает алгоритм релевантности. Релевантность контента на сайте поисковому запросу пользователя определяется до смешного просто — если текст содержит фразы, соответствующие поисковому запросу, то такой контент считается релевантным и готовится к публикации.

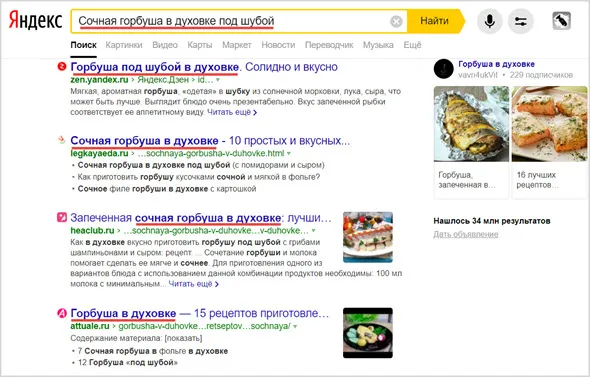
Фразы в тексте, соответствующие поисковому запросу, обычно называют «ключевыми словами» или «ключевыми фразами».

Чтобы поисковой системе было легче найти содержимое сайта, веб-мастера включают в текстовый контент релевантные ключевые слова. Это называется «оптимизация для поисковых систем».

После того как алгоритм релевантности нашел в базе данных (индексе) весь контент, соответствующий теме поискового запроса, все сотни и тысячи алгоритмов приступают к работе, чтобы определить качество и полезность контента.

• Оценка уникальности.
• Проверка достоверности и актуальности сведений.
• Объем и профессиональный уровень контента (информационная ценность).
• Авторитетность автора, репутация публикатора.
• Цитируемость – кто и как ссылается на данный контент на сторонних сайтах.
• И еще проверка контента и сайта в целом по нескольким сотням разных алгоритмов.

Некоторые алгоритмы поисковых систем хорошо известны и имеют названия.

• Алгоритм Яндекса ИКС определяет качество контента на сайте.
• Алгоритм Google «Колибри» предназначен для улучшенного поиска и ранжирования контента, написанного естественным разговорным языком.

Зная, что некоторые недобросовестные веб-мастера иногда идут на все, чтобы получить преимущество в рейтинге поисковых систем, разработчики Google и Yandex создали фильтры. С помощью фильтров поисковая система выявляет «серые», недобросовестные методы оптимизации сайтов и понижает такие ресурсы в результатах поиска по каждому поисковому запросу.