Рассмотрим любое поле k в K и множество всех многочленов kx от переменных x с коэффициентами в K. Многочлен P(x) из KX называется нередукцией поля k, если он нередуктивен. (x) множитель KX. Например, многочлен p(x) = x 2 +1 не является общим над R, но является рассеянным над C, потому что он разложен на множители из Cx: x 2 +1 = (x-i)(x +i).
Математика по полочкам
Задача на построение — это задача, требующая построения геометрических объектов с использованием только двух инструментов: компаса и линейки. Решение проблемы структуры заключается не только в построении подходящей структуры, но и в описании решения проблемы в виде последовательности уже известных стандартных структур.
Анализ
На этом этапе должны быть замечены такие зависимости между геометрическими данными и искомым, которые в дальнейшем позволят построить эту искомую геометрию.
Построение
1. в соответствии с анализом, все элементарные структуры, которые должны быть выполнены для решения проблемы, должны быть записаны в определенной последовательности, и
2. с помощью инструментов проектирования сразу же выполнить эти структуры на чертеже.
Доказательство
После построения схемы необходимо доказать, выполнены ли все условия задачи, т.е. удовлетворяет ли всем условиям задачи фигура, полученная из данных с окончательной структурой.
Основные задачи на построение
Задача 1. Построить треугольник с данными сторонами а, b, с.
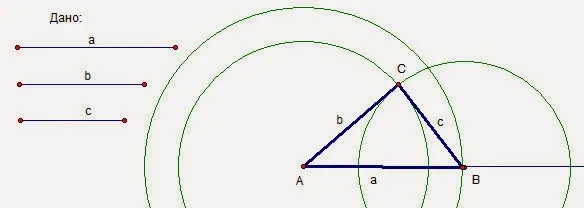
(2) Опишите окружность с центром A и радиусом A. Пусть b — пересечение с прямой.
(3) Опишите окружность из центра A, используя раствор циркуля, равный c, и из центра B, используя раствор циркуля, равный b. Пусть c — пересечение этих окружностей.
Задача 2. Построить угол, равный данному.
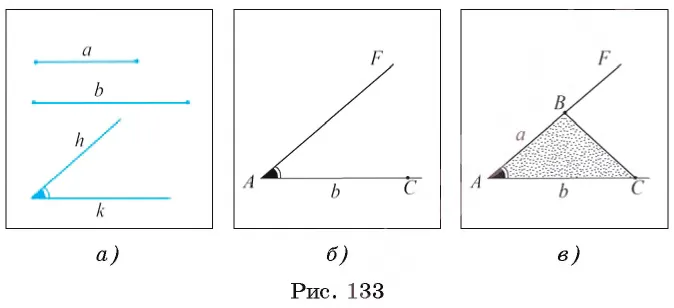
1) Начертите произвольную окружность в центре A заданного угла. Пусть b и c — пересечения окружностей по краям угла.
3) На радиусе AB начертите окружность с центром O. Покажите, что он содержит этот радиус в пересечении этого цикла.
4) Опишите окружность с центром M и радиусом BC. Точка K двух окружностей лежит на стороне угла.
Задача 3. Построить биссектрису данного угла А.
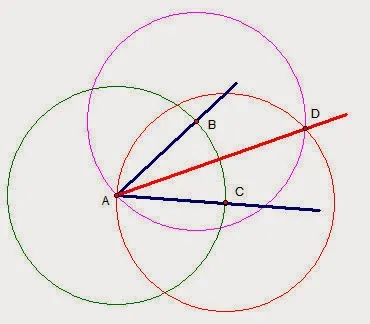
Построение: 1) Из вершины угла проведите окружность произвольного радиуса от центра. Пусть b и c — точки пересечения со сторонами угла. 2) Опишите окружности b и c одинакового радиуса. Пересечения, отличные от A. 3) Начертите AD. В объявлении угол А разделен на две части. Δbad = δABD = ΔACD после ρDAC (третья точка уравнения треугольника).
Задача 4. Провести серединный перпендикуляр к данному отрезку АВ.
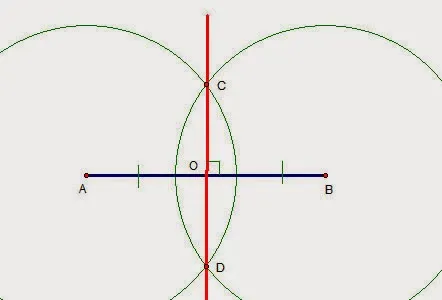
Построение: 1) Из точки A постройте окружность, радиус которой больше половины отрезка AB. 2) Из точки B проведите окружность A того же радиуса, что и точка A. 3) Окружности пересекаются в точках C и D. Прямая CD является необходимым перпендикуляром. CD перпендикулярен AB и AO = OB. По построению, каждые C и D равноудалены от A и B, поэтому эти точки должны находиться в середине перпендикуляра отрезка AB.
Задача 5. Разделить данный отрезок пополам.
Задача 6. Через данную точку О провести прямую, перпендикулярную данной прямой а.
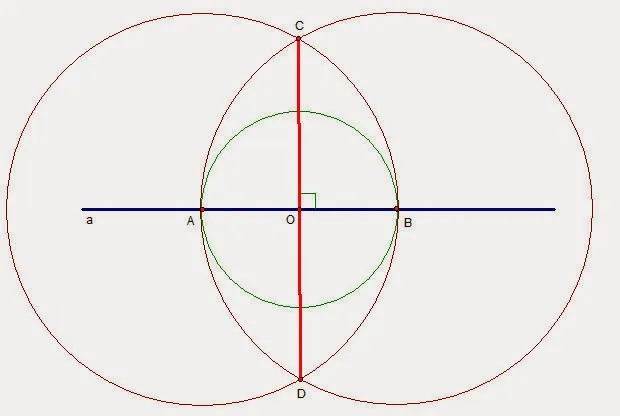
1) Из точек постройте окружность произвольного радиуса. Прямая A пересекается в двух точках A и B. 2) Постройте окружности радиуса AB из точек A и B. C и D — точки пересечения. 3) Нарисуйте линию CO. Получить OS ab. os ab, ΔACB, так как он равнобедренный (Ca = CB). Отрезок CO является высотой, так как это медиана данного треугольника (AO = AB).
Случай 2: точка o не находится в ряду.
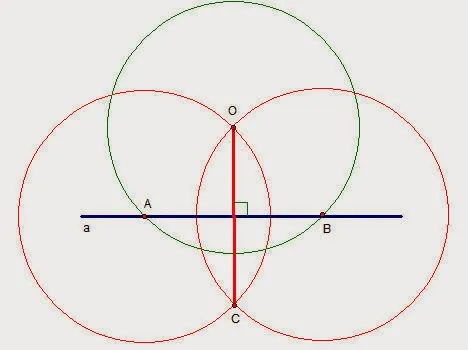
Точки o и c являются точками пересечения. 3) Нарисуйте линию OS. OS ab.
OS ab. потому что точки O и C равны концам AB и, следовательно, находятся в центре вертикали этого отрезка.
УПРАЖНЕНИЯ
Проведите прямую, проходящую через точку пересечения трех окружностей, O — точка пересечения этой прямой с AB. AO = OB.
6. Проведите линию через точку пересечения окружностей, O1 — точка пересечения этой линии с AO. AO1 = O1O.
2.(a) Используя компас и линейку, постройте прямоугольный треугольник из катетера и прилегающего к нему угла.
1. отметьте точку А на линии и проведите отрезок, равный отрезку А и отметьте точку В от точки А. 2. из точки В канал выпрямите перпендикулярно линии. 3. постройте из точки B угол, равный углу O. 4. стороны угла пересекают построенный перпендикуляр в точке C. ABC — искомый треугольник. ДОКАЗАТЕЛЬСТВО: В треугольнике ABC угол b правильный, сторона ab = a и угол abc равен углу O. Искомые треугольники равны по второму признаку равностороннего треугольника.
3.(a) Постройте треугольник изошеллы из основания и боковых сторон с помощью компаса и линейки. Возьмите любую сторону. (b) Используя компас и линейку, постройте треугольник с изошиной, простирающейся от основания и высоты до основания. Возьмите эти участки произвольно. Решение: (a) Поскольку стороны треугольника изошеллы равны, построение треугольника восходит к структуре, основанной на трех сторонах.
1. отметьте прямую точку A, из точки A проведите отрезок A, равный отрезку A, и отметьте точку B. 2. проведите окружность из центра B. Компас равен b. Подготовьте места встреч для этих циклов.
У треугольника ABC стороны равны A, B и B. Другими словами, треугольник ABC является равнобедренным и равен треугольнику, требуемому тремя сторонами.
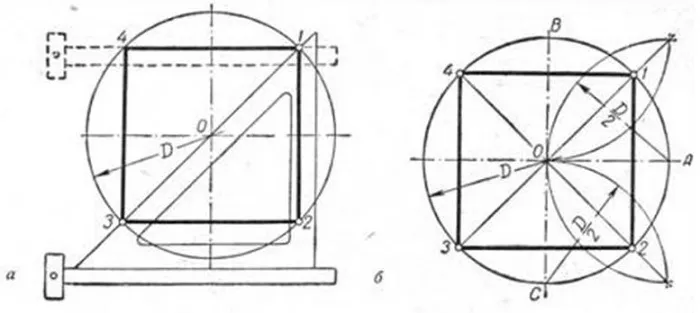
4.(a) Постройте прямоугольник с диагоналями и сторонами. Возьмите любой раздел. (b) Постройте прямоугольники с двумя сторонами. Возьмите любое заданное расстояние между ними. Решение: (a) Если известны диагонали и стороны прямоугольника, то из перпендикуляра и наклонной можно построить прямоугольный треугольник.
1. Отметьте точку A на линии M и постройте отрезок AD, равный отрезку a. 2. из точки A проведите окружность радиуса, равного отрезку D. 3. м из точки D проведите к прямой l вертикальный l перпендикуляр. 4. окружности, проведенные из точки l и точки A, пересекаются в точке C. 5. из точки D проведите окружность радиуса D. 6. из точки A проведите цикл радиуса CD.. Прямоугольник. ДОКАЗАТЕЛЬСТВО: ABCD — прямоугольник (из равенства треугольников ABD и ACD: AB = CD и AB ||| CD). Он также является прямоугольником, так как диагонали прямоугольника равны, и поэтому AC = BD по построению. 5.(a) Разделите этот раздел на три равные части. (b) Разделите этот раздел на пять равных частей. Решение: a)
3. на отрезке A3B произвольно возьмите точку O и постройте перпендикуляр M к прямой A3B через эту точку.
4. м от вертикальной прямой m, проведенной из точки A2 графика. B2 — пересечение этой прямой с частью AB.
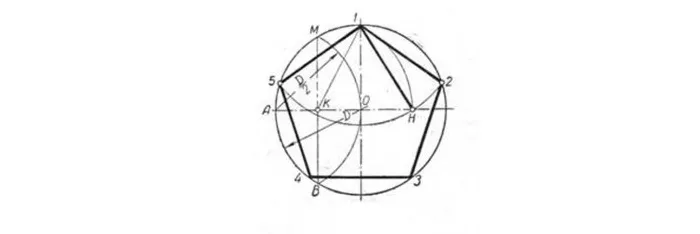
Возьмите компас, равный отрезку T.1 -T.H, и проведите кривую от T.1 до точки, где она касается окружности. Это метод вершин 2 и 5. Верхние 2 и 5 точки и верхние 3 и 4 точки выравниваются в конце.
Задача 1 (построение угла, равного данному)
Из заданного радиуса азбуки.
Предположим, что угловая DOF, удовлетворяющая рассматриваемой задаче, уже построена (рис. 130, a).
Пусть
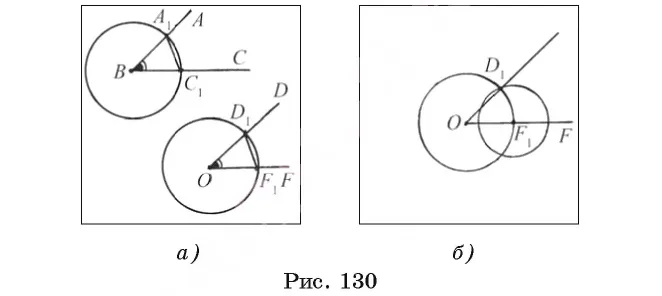
1) Нарисуйте цикл b, r). Где r — произвольный радиус, отметьте точки a1 и в1 пересечения с краями углов ABC.
2) Постройте цикл из 0, r), центр которого находится в точке того же радиуса r, и укажите точку пересечения f1 радиус.
3) Постройте цикл f1а, а1c1 (a).
4) d1 — цикл 0, r) и одно из пересечений f1а, а1c1 ) (рис. 130, б). Далее, угол d1цикла должно быть Докажите это.1из = ABC.
Равенство d1из = ABC вытекает из равенства треугольников1B.C.1 и г1из.1 из = ABC, что следует из равенства треугольников. Действительно, по конструкции a1b = d1o = c1b = f1o. Более того, из конструкции f1d1 =é1Больше.1 Таким образом, следовательно, треугольник a1B.C.1 и г1из.1 равны трем сторонам. d1из = а1B.C.1 т.е. заданный угол d1равен заданному углу ABC.
Задача 2 (построение серединного перпендикуляра к отрезку)
Постройте среднюю точку перпендикуляра к определенному отрезку AB.
Рассмотрите обоснование, которое помогает создать требуемую конструкцию. Предположим, что половой акт A построен на участке AB (рис. 131, a). Пусть средние точки f и d = od. BF = BD, так как прямоугольные треугольники FOB и DOOB равны двум катетам; другими словами, точки f и d лежат в окружностях (b, bf) и bf> ob. Аналогично, AF = AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко проверить, что AF = BF. Таким образом, точки f и d также лежат в окружностях (a, bf).
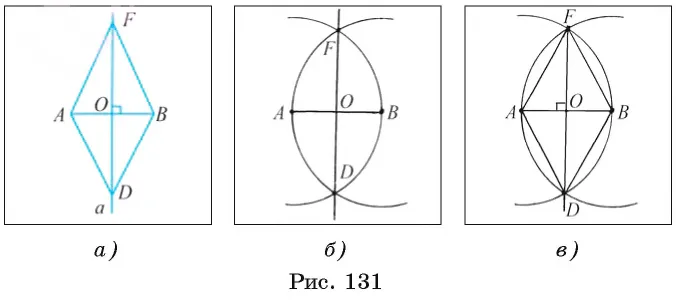
1) Нарисуйте окружности a, r) и b, r). Здесь r — это ab. Пусть r = ab: a, ab) и b, ab) (рис. 131, б).
2) Отметьте точки f и d окружностей (a, ab) и (b, ab).
(3) Далее, прямая FD имеет средний размер в AB. Докажите это.
Рассмотрим треугольники fashionable и FBD (рис. 131, c). У этих треугольников равны три стороны. Следовательно, afd = bfd. Таким образом, в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, высота и медиана, то есть FO, является медианой AB.
Задача 3 (построение биссектрисы угла)
Строится разбиение заданного угла ABC.
Предположим, что биссектриса угла ABC построена (рис. 132 A). Предположим, что f и d находятся на сторонах угла, bf = bd, o = fd be, а t пересекает перекладину поперек луча. Из равенства прямоугольных треугольников fot и dot (fo = od, наименьшая сторона OT общая), ft = dt, т.е. точка t должна принадлежать циклу равных лучей с центрами f и d. Построив точку t, мы строим нижнюю часть BT этого угла.
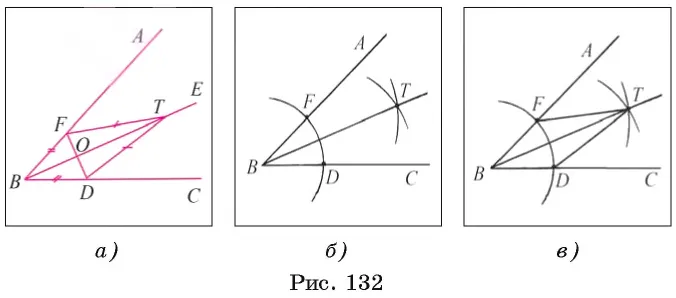
(1) Постройте цикл B, r1 ) любого радиуса r1 с центром в вершине B этого угла (рис. 132, b).
2) Цикл b, r), отметив точки f и d, где угол пересекает стороны B и BC.
3) Постройте окружности f, r2 (и d, r2 ), r2> fd. Отметим пересечение t t в пределах этого угла.
4) Начертите радиус BT. Требуется лучевая BT. Докажите это.
Рассмотрим треугольники BFT и BDT (рис. 132, C). Эти треугольники имеют равные три стороны (из построений Bf = BD и FT = DT, BT — общая сторона). Равенство этих треугольников означает, что FBT = DBT, то есть радиус BT является биссектрисой угла ABC.
Исходя из того, что диагонали каждого квадрата пересекаются в середине круга и находятся под углом 45° к его оси, действуйте следующим образом. Используя линейку и угол в 45 градусов (см. схему), отметьте вершины t. 1 и т. 3.3.
Примеры задач на построение
Начертите угол, равный заданному углу
Из заданного радиуса начертите угол, равный заданному углу.
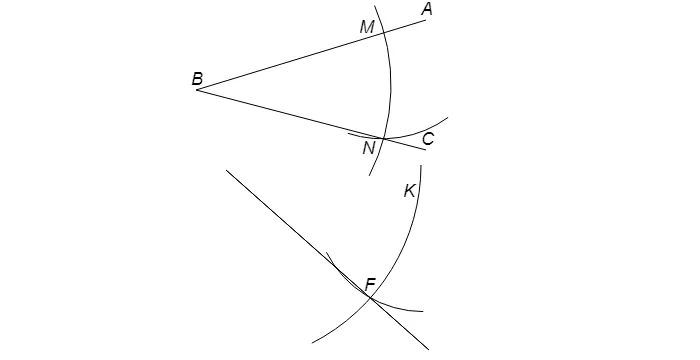
Угол между вершиной A и лучом OM задан, как показано на рисунке 84. Необходимо построить угол, равный A, так, чтобы одна из его граней совпадала с радиусом ОМ.
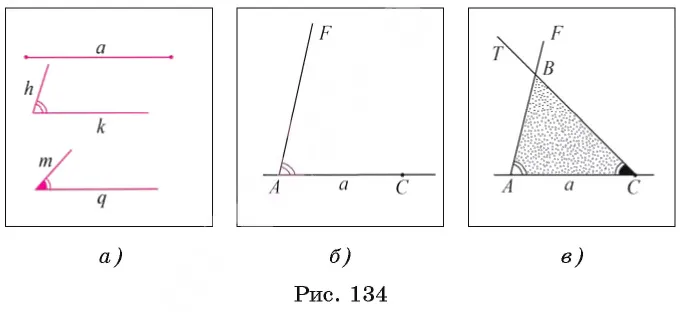
Начертите окружность произвольного радиуса с центром в вершине A под заданным углом. Окружность пересекает грань угла в точках B и C (рис. 85, a). Затем нарисуйте окружность радиуса с центром в начальной точке заданного радиуса OM. Радиусы пересекаются в точке D (рис. 85, b). Затем начертите окружность с центром D и радиусом BC. Окружности с центрами O и D пересекаются в двух точках. Одна из этих точек обозначена E. Докажите, что MOE — искомый угол.
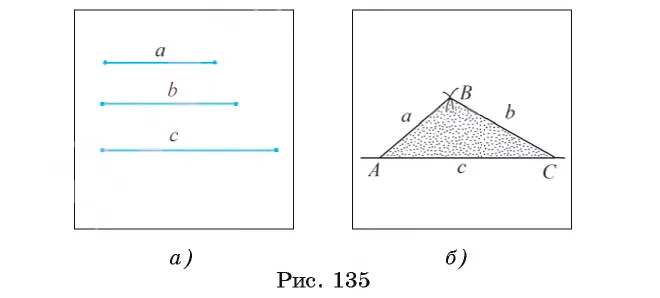
Рассмотрим треугольники ABC и ODE. AB и AC — радиусы окружности с центром в A, а OD и OE — радиусы окружности с центром в O (см. рис. 85b). Из построения следует, что эти окружности имеют равные радиусы, поэтому AB = ΟD, ΑC = ΟΕ. Также из построения следует, что BC = DE.
Таким образом, можно сделать вывод, чтоΔABC =ΔODE от трех сторон; поэтому ∠DOE = ∠BAC, т.е. построенный угол MOE равен заданному углу A.
Такую же конструкцию можно выполнить и на земле, используя вместо компаса веревку.
Построение биссектрис углов
Нарисуйте биссектрису угла.
Заданный угол BAC показан на рисунке 86. Начертите окружность произвольного радиуса с центром A. Она пересекает стороны угла в точках B и C.
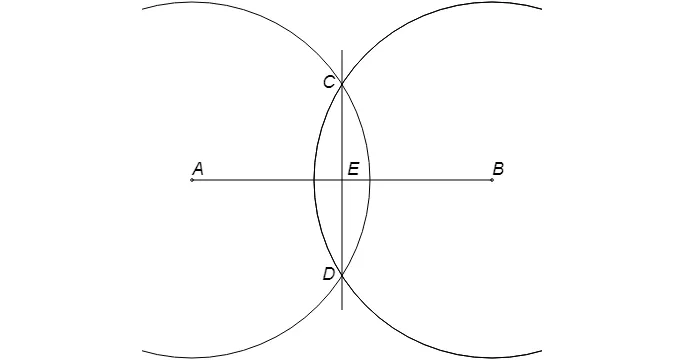
Затем начертите две окружности одинакового радиуса BC с центрами B и C (на схеме показаны только части этих окружностей). Они пересекаются в двух точках, по крайней мере, одна из которых находится внутри угла. Обозначим через E. Докажите, что AE — биссектриса угла BAC.
Рассмотрим треугольники ACE и ABE. Они равны с трех сторон. Фактически, AE является общей стороной — AC и AB совпадают с радиусами одной и той же окружности — CE=BE из построения.
Треугольники ACE и ABE равны, значит, ∠CAE=∠BAE. Это означает, что радиус AE является биссектрисой данного угла BAC.
Можете ли вы разделить этот угол на два равных угла с помощью компаса и линейки? Очевидно, что это можно сделать, разделив угол.
Также можно разделить угол на четыре равных угла. Это можно сделать, разделив его пополам, а затем снова разделив каждую половину пополам.
Можно ли разделить угол на три равных угла с помощью компаса и линейки? Эта проблема, известная как проблема стрижки, привлекала внимание математиков на протяжении многих веков. Только в XIX веке выяснилось, что создать такую конструкцию под любым заданным углом невозможно.
Построение перпендикулярных прямых
Даны прямая линия и точка на ней. Строится прямая, проходящая через заданную точку и перпендикулярная заданной прямой.
Прямая α и точка М, принадлежащая этой прямой, показаны на рисунке 87.
Постройте равные отрезки MA и MB на радиусе прямой α, начиная с точки M. Затем начертите две окружности с центрами A и B радиуса AB. Они пересекаются в точках P и Q.
Проведите прямую через точку M и одну из этих точек. Постройте прямую MR (см. рис. 87) и докажите, что она является необходимой, т.е. перпендикулярна прямой a.
На самом деле, медиана PM равнобедренного треугольника RV также является высотой, поэтому PM⊥a.
Построение середины отрезка
Создайте центр секции.
Пусть AB обозначает этот раздел. Постройте два цикла с радиусами A и B радиусами AB. Пересекаются в точках P и Q. Постройте линию PQ. Точка пересечения этой линии с частью AB является искомой серединой отрезка AB.
Действительно, у треугольников APQ и BPQ равны три стороны, поэтому ρ1 = ρ2 (рис. 89).
Таким образом, участок RO является биссектрисой равнобедренного треугольника ARB и, следовательно, медианой. Другими словами, точка O является центром отрезка AB.
Однако, по словам профессоров математики, простое доказательство великой теоремы Фермата с помощью потока букв с решением треугольника недавно было значительно сокращено. Теперь они обычно присылают ему доказательства по делу Римана.
Построение перпендикулярных прямых
Пример 1
Есть один момент.
У него есть линия и точка. Проведите прямую через существующую точку, которая вместе с прямой составляет прямой угол.
Шаг 1. Нарисуйте окружность r произвольного радиуса с центром O. Цикл является касательной к точкам a и b.
Шаг 2. Постройте цикл радиуса AB из имеющихся точек. Точки c и d являются пересечениями окружностей.
С помощью линейки проведите прямую линию через t O и один из t. C или т. D, например, прямой участок OC.
Докажите, что прямая OC перпендикулярна a.
Имеется две секции AC и CB. Полученный треугольник равен согласно третьей точке тригонометрического уравнения. Тогда прямая CO перпендикулярна AB.
Пример 2
Точка o находится вне линии a.
Проведите окружность из точки o в точку r. Линия должна проходить насквозь. A и B — точки соприкосновения с линией.
Оставьте радиус как раньше и нарисуйте окружность в центральных точках A и B. Точка o1 — Это точка их пересечения.
Проведите линию, соединяющую o и o1.
Доказательство заключается в следующем.
2 строки o.1 AB пересекается в точке c. Третья точка равенства всех треугольников AOB = bo1A. Этот вывод основан на том, что угол oac = o1AC. Одноименные треугольники также равны (согласно первому равенству всех треугольников).
Таким образом, угол oac = o1CA, и, учитывая близость углов, мы делаем вывод, что это правильные углы. Это означает, что oC — это вертикальная часть, принятая за o. Проблема решена.
Построение параллельных (непересекающихся) прямых
Есть прямые и непрямые. Эта линия не делает этого.
Необходимо отметить, что прямая линия, проходящая через t A и параллельно прямой.
Произвольная точка на прямой называется B. Используя компас, постройте цикл радиуса AB с центром t. B. На пересечении окружностей, прямых, запишите t. C.
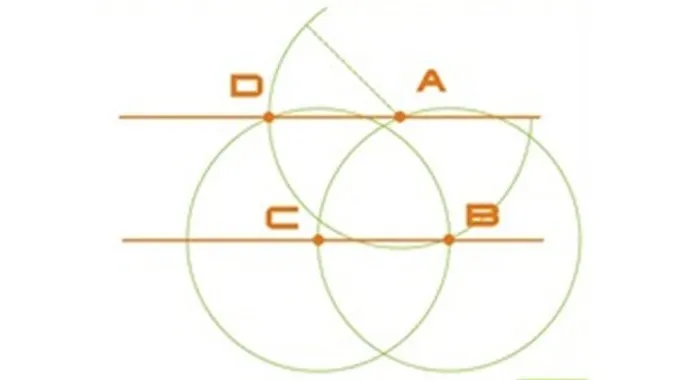
Сохраняя тот же радиус, проектируется еще один цикл. На этот раз в центре C. Если вычисления верны, то лук должен пройти через T. B.
Окружность с тем же лучом AB и центром T. A. Точка пересечения второго и третьего циклов называется d. Третий цикл также проходит через T. Второй цикл называется d. Третий цикл проходит через T. Третий цикл также проходит через T. Третий цикл проходит через T. B. Если расчеты верны.
Проведите прямую линию через точки A и d. Это будет параллельно первой линии. Наконец, вы получаете две параллельные прямые BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения прямоугольных треугольников, зарегистрированных в круге:.
Обратите внимание на отрезок AB, длина которого равна a.
Возьмите компас. Установите иглу на t. a и отрезок с карандашом в точке t. B. Нарисуйте круг. Полученный радиус окружности равен длине отрезка AB.
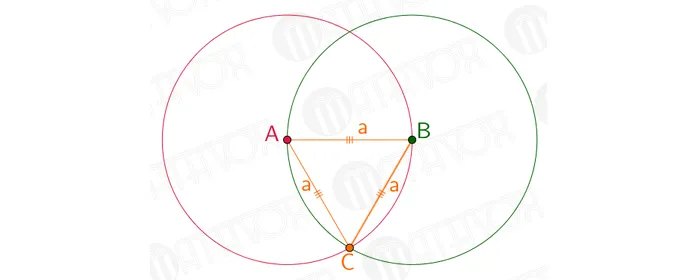
Затем поместите иглу на вершину t. B и площадь с карандашом в момент t. A. Планируется круг. Следовательно, его радиус равен длине отрезка AB.
На рисунке окружности пересекаются в двух точках. Затем установите t. A и B и один из вышеупомянутых пунктов. В результате получается равносторонний треугольник.
Стороны такого треугольника равны лучам двух равных по длине циклов a. Проблема решена.








